认知无线网络中一种基于博弈的自适应功率控制算法
2014-12-14杨浩磊
朱 江,杨浩磊,韩 超
(重庆邮电大学移动通信技术重庆市重点实验室,重庆400065)
0 引言
随着无线通信的快速发展,频谱资源变得越发紧张,而且无线频谱资源是不可再生资源,它的分配利用通常是由无线电法规部门制定的,这些部门采用的是固定频带分配原则,这种原则和方法会造成频谱资源日趋缺失。另一方面,这个分配制度会使包括郊区在内的各类地区在大部分时间内频带没有被占用,造成频谱利用率很低、频谱资源浪费的现象。因此,提高频谱利用率是一个解决频谱资源稀缺的很好方法。提高频谱利用率的方法是:当主用户处于空闲时,在对主用户不造成干扰的情况下,认知用户接入空闲频段,能够很好地提高认知无线电频谱的利用率[1-5]。
认知无线电的研究中,其中一个方面是功率控制,功率控制是在满足用户公平性的基础上,通过有效地控制用户的发射功率,以满足用户的通信质量需求[6]。文献[7]中,研究了在认知无线电网络中采用联合速率与功率控制对性能的影响,采用的方法为:在尊重主用户到达速率的条件下,调节次用户传输速率来增大并行传输区域。文献[8]中,提出了采用波束成型与功率控制技术来克服感知时间与吞吐量的折中问题,文中采用了修改后的注水算法,并且最小化了对主用户的干扰,克服了感知吞吐量与感知时间的折中问题。文献[9]中,研究了在功率控制与竞争控制下的认知无线电网络中的集中干扰模型,功率控制的提出是为了控制认知节点的发射功率,在媒体访问控制层的竞争控制是为了协调认知节点间的传输要求。
在本文中,功率控制算法能起到省电作用。在满足通信质量要求的情况下,通过减少发射功率就可以达到省电目的,因为终端,如手机等大多是通过电池来提供能量,如果减少了发射功率,自然就会延长电池等的使用时间[10-11]。目前关于功率控制的算法很多,但仍然有很多问题,例如,会出现远近不公平性现象,当认知用户距离基站远时,认知用户的发射功率增大,而信干噪比(signal to interference plus noise ratio,SINR)却很小,不能满足通信需求[12-14]。例如文献[15]中的K-G算法虽然对SINR的阀值进行了设定,但该算法只满足上限阀值,不一定满足下限阀值,且不能克服远近不公平性;文献[16]中的PG-K-G算法虽然对K-G算法进行了改进,克服了远近不公平性,但功率消耗相对较高,不利于省电;而improve算法能够在满足通信质量的条件下,既克服了认知无线电的远近不公平性,又满足了省电要求。本文研究的算法还可以在SINR不满足目标SINR要求的范围内时,通过自适应调整参数,改变其SINR值来适应目标信干比。
1 系统模型
假定一个分布式网络小区中有1个基站及N个认知用户。该网络小区为圆形小区,且基站位于圆心处。认知用户随机分布于小区内,认知用户间存在相互干扰。
假设用户i与基站的距离为di;A为常数增益;m为路径衰落因子,其值一般为2 -6,则信道增益h为hi=A/dmi;设用户i的发射功率为pi,则基站接收的功率为hipi;cij为用户间扩频码的相关系数;设噪声为vi,则在通信中小区内其他用户对用户i的干扰为。因此,可以导出基站接收到用户i的SINR为
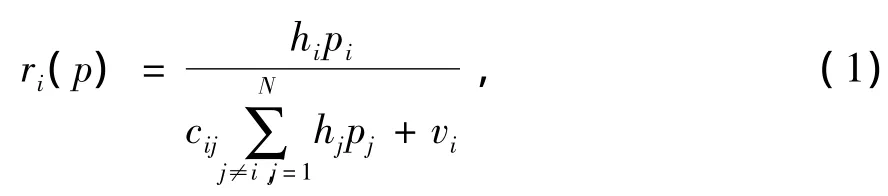
2 自适应功率控制博弈算法
2.1 博弈论与效用函数
由于在这个系统模型中,发射功率是可以控制的,是典型的分布式功率控制,这与博弈论中的非合作博弈中的完全静态博弈很相似,因此,可以通过非合作功率博弈效用函数来表达功率控制的过程。
非合作功率博弈是指每一个网络节点以自私的方式寻求自己最大发射功率而造成每个网络节点间相互冲突的一种博弈,并最终使每个认知用户的发射功率达到某种平衡。假设 J=[Γ,{Pj},{uj(·)}]为认知无线电的非合作功率博弈策略;局中人为所有的认知用户,Γ ={1,2,…,N}是认知用户的集合;Pj={p1,p2,…,pN}是认知用户j的发射功率集合;uj(·)为认知用户的效用函数。定义效用函数为
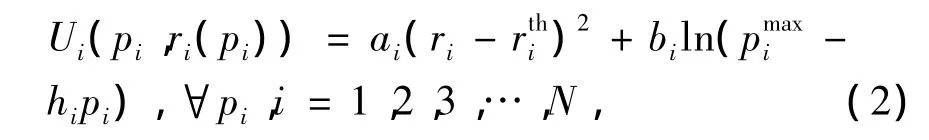
(2)式中:ai与bi为影响因子,其值为非负;rtih为SINR最小的阀值;pmiax为最大接收功率;ai(rirtih)2是代价函数,当ri>rtih时,随着ri的不断增大,所消耗的发射功率就越大,就会越耗电,因而所要付出的代价就越大。同样,对于ln(pmiax-hipi),因为pmiax>hipi,当认知用户与基站的距离越远时,信道增益就越小,所允许的发射功率就越大,因而克服了认知无线电的远近不公平性。
设ki=bi/ai,当SINR超过最大阀值rtari时,就要通过自适应调整参数,使信干比满足所允许的范围,自适应调整参数为

2.2 功率博弈均衡存在性与唯一性分析
纳什均衡是一种策略组合,使得每个网络节点的策略是对其他网络节点的最优反应。如果没有节点单独行动而增加收益的话,那么这个策略组合叫做纳什均衡。但是,因为在分布式网络中,每一个认知用户都是以自私的方式通过最佳功率水平来实现自己利益最大化,会使纳什均衡发射功率可能不存在或不唯一。因此,我们在求纳什均衡发射功率前,首先要证明其是否存在,以及纳什均衡值是否唯一。
定理1 本文中的非合作功率博弈模型存在纳什均衡解,而且纳什均衡解是唯一的。
证明过程参考附录A。
2.3 利用牛顿迭代法求解发射功率
由博弈论知识知,在一个通信系统中,任何单方面改变功率所得的系统收益不会比在纳什均衡点的纳什均衡发射功率所得的系统收益高。设纳什均衡发射功率为p*i,有
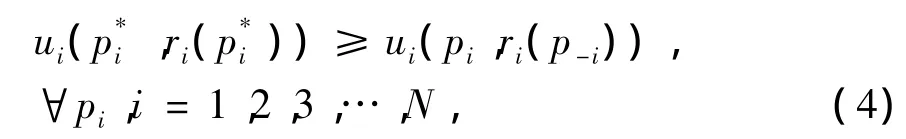
(4)式中:ui(p*i,ri(p*i))为在纳什均衡条件下的效用函数;ui(pi,ri(p*-i))为在非纳什均衡条件下的效用函数;r(p-i)为除了用户i的其他用户的信干比。
根据拉格朗日算法,对ui(p*i,ri(p*i))求导得

将(1)式代入(5)式得
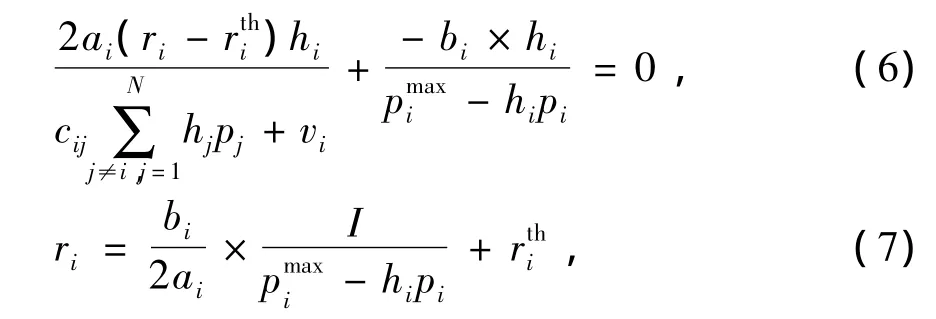
(7)式中,
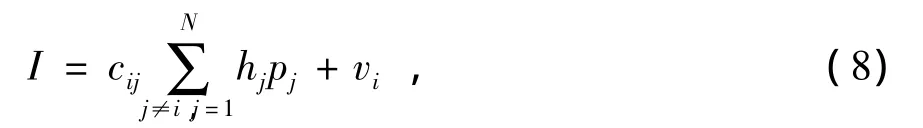
把(7)式代入(1)式得

运用牛顿迭代法得到迭代n次的发射功率为
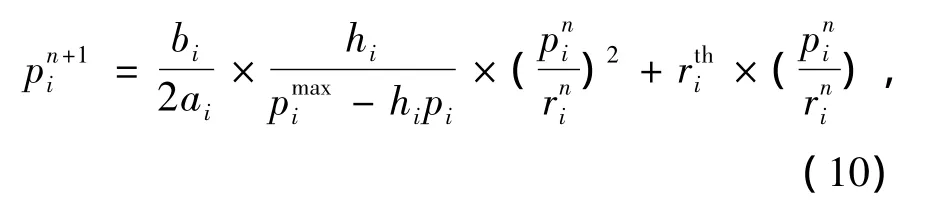
因为发射功率是有限度的,为pmaxi,则

2.4 纳什均衡发射功率的流程图
通过拉格朗日求导,可以得出初始信干比,进而求得初始发射功率,通过牛顿迭代法迭代,当第n次迭代与n-1次迭代小于迭代误差时,该次迭代的值就是我们要找的纳什均衡发射功率。如图1为求得纳什均衡发射功率的具体流程图。

图1 纳什均衡发射功率流程图Fig.1 Nash equilibrium transmit power flow chart
2.5 公平性因子
公平性因子是指衡量SINR及其SINR期望之间的偏离程度,可以用它来体现认知无线电的远近不公平性。如果公平性因子数据的波动越大,则说明该数据越不公平。
SINR的期望为

公平性因子为

3 仿真结果和性能分析
本文采用MATLAB进行仿真。本文不考虑阴影衰落,快衰落及多径时延对信号的影响,且噪声固定为vi=5×10-12W。假设认知用户为N=20,且随机处于半径为di=1 km的圆形小区内,扩频码为256位的Walsh码,因而可得到cij=1/256。信道增益hi=A/dmi,其中 A=10-11,m=4.2,认知用户的初始发射功率为p0i=2.22 ×10-16W,最大允许功率为pmiax=50 mw。
信干噪比阀值的设定会对系统性能造成影响,比如改变信干噪比的阀值会改变SINR。图2为KG算法及PG-K-G算法中通过改变SINR最大阀值对SINR影响的仿真图。图3为improve算法中通过改变SINR最低阀值对SINR影响的仿真图。图2,图3均是在SINR达到收敛状态下随机抽取用户15的SINR。由图2,图3可知,K-G算法与PG-K-G算法与信干比最大阀值rtiar有关,且为线性相关。而improve算法与信干噪比最低阀值rtih呈线性相关。这是因为在K-G算法以及PG-K-G算法中,其效用函数包含了rtiar对SINR的限制,而不包含rtih,所以K-G算法及PG-K-G算法中最低阀值rtih对SINR不造成什么影响。同样在improve算法中,只加入了rtih来改变用户的SINR,而没有rtiar,所以在improve算法中最大阀值rtiar的设定对SINR没有影响。由于在图2和图3中,阀值设定对SINR的影响都是线性的,并无特殊之处,为了不失一般性,设定最低阀值rtih=6,且为了考虑省电,设定最大阀值rtiar=8。
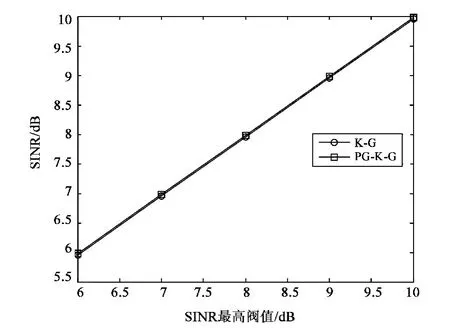
图2 K-G,PG-K-G算法中次用户15的rtiar设定对SINR的影响Fig.2 Influence of SINR from rtiarof the second user 15 in tthe K-G algorithm and he PG-K-G algorithm
在ki=2×1011条件下,图4分别为采用K-G算法,PG-K-G算法,improve算法的次用户10的SINR,次用户10是随机抽取的,可以用其他用户代替。由图4可知,次用户的SINR随着迭代次数的增加,3种算法收敛。这是由于纳什均衡发射功率的存在且唯一,随着迭代次数的增加,会使得最终的发射功率收敛,因而信干噪比收敛,这也从仿真的角度证明了纳什均衡的存在性与唯一性。

图3 improve算法中次用户15的rtih设定对SINR的影响Fig.3 Influence of SINR from rtihof the second user 15 in the improve algorithm

图4 3种算法中次用户10(随机选择)的SINRFig.4 Second user 10(randomly chosen)in three algorithms SINR
图5分别为K-G算法,PG-K-G算法,improve算法的SINR公平因子随着迭代次数的变化的曲线图,由图5可知,采用K-G算法的不同认知用户间的SINR公平因子值不为零,而采用PG-K-G算法,improve算法的不同用户的SINR公平因子均为零。在图6中分别给出了K-G算法,PG-K-G算法,improve算法的平均发射功率随着迭代次数变化的曲线图,由图6可知,improve算法的平均发射功率比PG-K-G算法的平均发射功率要小。分析可知:在K-G算法中,其公平因子不为零是因为各个次用户间的SINR不相等,而SINR不相等的原因是基站与认知用户的距离越远,SINR就越小,发射功率却越大,并因此产生了远近效应。在PG-K-G算法和improve算法中,SINR与用户离基站的距离的远近无关,发射功率与用户离基站的距离的远近成正相关,故而其公平因子为零,证明了各个次用户间的SINR是相等的,因而有效地克服了远近不公平性,但由图6可知,PG-K-G算法中其发射功率较improve算法相对过高,消耗功率很大,不利于省电,而improve算法中,既克服了远近不公平性,又在SINR允许范围内消耗较小的发射功率,故而可以省电。
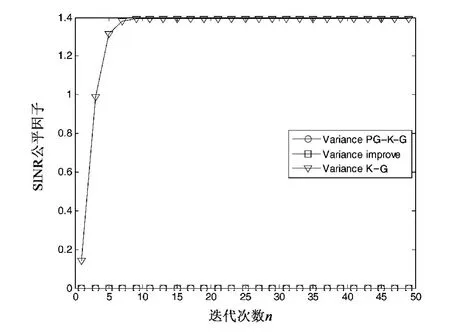
图5 3种算法的SINR公平因子比较Fig.5 SINR fairness factor comparison of the three algorithm
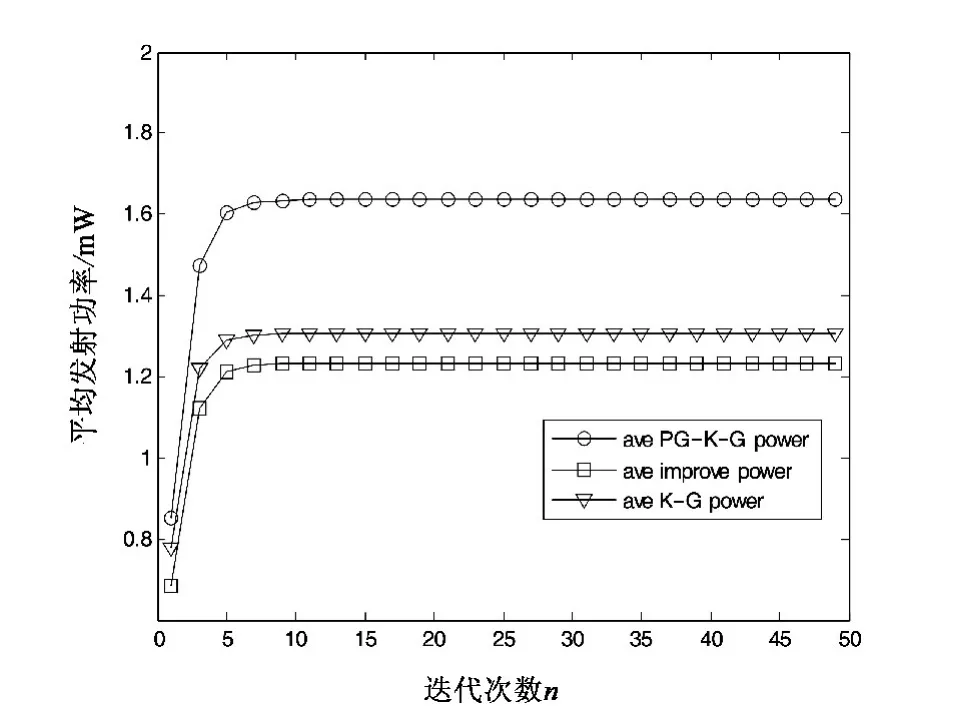
图6 3种算法的平均发射功率比较Fig.6 Comparison of three algorithms of the average transmission power
改变ki的值,当ki=2×1013时,图7分别为improve算法以及对ki自适应调整参数后的improve算法。从图7中可知,improve算法中,迭代几次后,由于SINR的阀值设定范围为6—8,因而SINR超过了最大阀值rtari。然而在自适应调整参数improve算法中,当发现SINR值超过了最大阀值后,通过自适应调整参数,使SINR恢复到允许范围值以内,满足了省电的要求。因而,经过自适应调整后,SINR在阀值范围内。
4 结束语

图7 improve算法自适应调节前后对比Fig.7 Improve algorithm adaptive contrast before and after the adjustment
本文提出了基于SINR的博弈功率控制机制,并在SINR允许的范围内减少了功率消耗以达到省电目的。仿真结果表明,与K-G算法比较,克服了认知无线电中远近不公平的现象,满足了不同用户公平的共享频谱的需求;与PG-K-G算法比较,在不影响通信的情况下,通过较少的功率的消耗,达到了省电的目的。并且当SINR超出最大阀值的情况下,通过自适应改变参数调节SINR,使SINR达到允许的范围,减少功率不必要的浪费。
[1]MITOLA J,MAQUIRE G.Making Software Radios More Personal[J].IEEE Personal Communications,1999,6(4):13-18.
[2]WANG Beibei,LIU K.Advances in cognitive radio networks:a survey[J].IEEE Journal of Selected Topics in Signal Processing,2011,5(1):5-23.
[3]ZHAO Q,SADLE B.A survey of dynamic spectrum access[J].IEEE Signal Processing Magazine,2007,24(3):79-89.
[4]LU L,ZHOU X,ONUNKWO U.Ten years of research in spectrum sensing and sharing in cognitive radio [J].Wireless Commun,2012,1(28):1-16.
[5]郭云玮,高俊,刘全.认知无线电中频谱感知技术的研究发展[J].中兴通讯技术,2010,16(6):39-43.GUO Yunwei,GAO Jun,LIU Quan.A Survey on Spectrum Sensing Techniques in lognitive Radio Network[J].ZIE communications,2010,16(6):39-43.
[6]郭雁.基于博弈论的认知无线电功率控制算法研究[D].北京:北京邮电大学,2010.GUO Yan.The research of the power control algorithm based on game theory in the cognitive radio[D].Beijing:Beijing university of posts and telecommunications,2010.
[7]SANCHEZ S,SOUZA R.Rate and Energy Efficient Power Control in a Cognitive Radio Ad Hoc Network[J].IEEE Signal Processing Magazine,2013,20(5):451-454.
[8]FATTAH A,MATIN M.Joint beamforming and power control to overcome tradeoff between throughput-sensing in cognitive radio networks[C]//IEEE.IEEE Symposium on Computers & Informatics.New York:IEEE Press,2012:150-153.
[9]CHEN Zengmao,WANG Chengxiang.Aggregate interference modeling in cognitive radio networks with power and contention control[J].IEEE transactions on Communications,2012,60(2):456-468.
[10]SOROOSHYARI S,TAN C,CHIANG M.Power control for cognitive radio networks:Axioms,algorithms,and analysis[J].IEEE/ACM Trans Netw,2012,20(3):878-891.
[11]LEVORATO M,MITRA U,ZORZI M.Cognitive interference management in retransmission-based wirelessnetworks[J].IEEE Trans Inf Theory,2012,58(5):3023-3046.
[12]WANG S,HUANG F,ZHOU Z H.Fast power allocation algorithm for cognitive radio networks[C]//IEEE.IEEE Commun Lett.New York:IEEE Press,2011,15(8):845-847.
[13]XING Yiping,CHANDRAMOULI R.Stochastic learning solution for distributed discrete power control game in wireless data networks[J].IEEE/ACM Transactions on Networking,2008,16(4):932-944.
[14]NI Q ,ZARAKOVITIS C.Nash bargaining game theoretic scheduling for joint channel and power allocation in cognitive radio systems[J].IEEE Selected Areas Commun,2012,30(1):70-81.
[15]KOSKIE S,GAJIC Z.A nash game algorithm for SIRBased power control in 3G wireless CDMA networks[J].IEEE/ACM Trans on Networking,2005,13(5):1017-1026.
[16]罗荣华,杨震.认知无线电系统中一种新的自适应功率控制算法[J].信号处理,2010,26(8):1257-1262.LUO Ronghua,YANG Zhen.An new adaptive power control algorithm in the cognitive radio[J].Signal Process,2010,26(8):1257-1262.
附录A
功率博弈均衡的均在性与唯一性证明
1 纳什均衡的存在性
要证明纳什均衡的存在性,须证明如下2点。
1)效用函数是一个非空有界闭凸集,即是有限博弈,局中元素都是有限个数的,显然,这个条件是成立的。
2)证明效用函数是连续的,拟凹函数。
证明:效用函数显然在pi上连续,又因为
显然,该函数为凹函数,也即是拟凹函数。
因而得证纳什均衡的存在性。
2 纳什均衡的唯一性
证明唯一性需要证明如下3个条件。
1)正性,即R(p)>0;
2)单调性,即如果p>p',则R(p)>R(p');
3)可扩展性,即如果有a>1,则有aR(p)>R(ap);
证明:对于1)因为

得证。
对于2)当p>p'时

对于3) 设
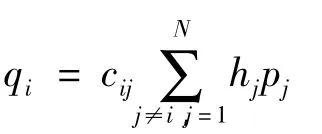
当v2i>aq2i时,定有aR(pi)-R(api)>0
得证。因而证明了纳什均衡的唯一性。
