基于实干扰对齐技术的两用户中继辅助信道的安全自由度分析
2014-12-14朱茂娟雷维嘉谢显中
朱茂娟,雷维嘉,谢显中,张 琴
(重庆邮电大学移动通信技术重庆市重点实验室,重庆400065)
0 引言
在无线通信中,信号容易被窃听,信息安全是一个重要的问题。传统上,信息安全多采用保密编码的方式在高层实现。作为另一种实现信息安全传输的手段,物理层安全技术是近年来无线通信的重要研究课题。干扰对齐(interference alignment,IA)技术是可用于提高保密通信安全性的物理层技术之一。干扰对齐是发送端根据信道状态对发送信号进行预处理,使在接收端能将接收到的信号中有用信号对齐到接收信号的一个子空间中,而来自其他所有非期望发送机的干扰信号对齐到另一个与期望信号子空间线性独立的干扰子空间中,从而在该接收端可以将期望信号解码出来。干扰对齐技术的目标是提高干扰信道的信道容量。干扰对齐也可用于安全通信,在窃听端将信号与噪声对齐,使窃听端无法解码信号。目前干扰对齐技术被用于多种信道中以提高安全性能,其主要性能指标是保密速率、保密容量和安全自由度。安全自由度可描述信号子空间的维数,安全自由度越高说明保密性能越好。
目前已经有很多文献对安全干扰对齐系统的安全自由度进行了分析和研究。文献[1]研究了K用户干扰信道中保密消息传输时,采用嵌套格码和分层编码技术,分析结果表明,在K=3时,总安全自由度小于3/4。文献[2]也对K用户干扰信道的安全通信进行研究,信息传输时先采用保密预编码,然后采用文献[3]中的经典干扰对齐方案,在K=3时,总安全自由度为3/4。文献[4]研究了有1个外部窃听者的K用户干扰信道中,采用实干扰对齐技术能获得的总安全自由度,在K=3时,总安全自由度等于1。文献[5]对K用户干扰信道条件下的3种情况:保密消息、1个外部窃听者,以及有1个外部窃听者时保密消息的传输进行了研究,通过使用结构化信号、结构化协作干扰、信道前缀(channel prefixing)和渐进实干扰对齐等技术,可获得大于0的总安全自由度,在K=3时,安全自由度可达到6/5。
实干扰对齐技术用于实信道系数情况下的干扰消除。近几年很多文献中都用到实干扰对齐来提升系统的安全自由度。文献[6]研究有辅助者的高斯窃听信道,采用基于实干扰对齐和协作干扰的方案,分别得到了无辅助者、1个辅助者和M个辅助者的安全自由度。文献[7]研究高斯窃听信道,在无窃听端信道状态信息时,有M个辅助者时的实干扰对齐方案,并分析得到了安全自由度。文献[8]对4种基本的一跳无线网络进行研究,采用实干扰对齐方案分别得出了高斯窃听信道、高斯广播信道、高斯干扰信道和高斯多址接入信道的总安全自由度。
在基于物理层技术的安全通信中,使用辅助者来协助提高安全传输的性能是常用的一种手段。辅助者有2种使用方式:一种是作为中继,帮助发送端发送有用信号;一种是作为干扰源,向窃听者发送人工干扰,降低其获取安全信息的能力。可使用2种方式中的一种,也可以2种方式混合使用。近年来,当辅助者作为中继时的转发方案,如放大转发、解码转发、压缩转发等,以及中继系统的方案得到广泛的研究。具有中继时的安全干扰对齐技术的文献还较少,文献[9]研究了安全干扰对齐中的中继方案,研究两用户中继辅助干扰信道(源端与目的端有直接链路)的保密问题。研究中将中继信道分为两类:一是信道系数为实数。文献[9]给出了一种中继方式,通过中继将两用户的干扰信道由X信道转化为一个Z信道(称为智能中继技术),利用实干扰对齐可得安全自由度为1,而若无中继时的安全自由度为2/3;二是信道系数为复数,此时,若中继采用放大转发方式,用实干扰对齐可获得2/3的安全自由度;若中继采用广泛线性化处理可获得的安全自由度为1。
本文针对两用户中继辅助干扰信道模型,在实信道系数的情况下的安全干扰对齐技术进行研究。该方案中,中继端除了采用放大转发方式转发发送端的信号外,还同时发送协作干扰信号。我们采用实干扰对齐技术,并对安全自由度进行分析,结果表明,安全自由度可达到1。本方案的安全自由度高于文献[8]的无中继方案。而和文献[9]中的方案相比,虽然安全自由度相同,但本文的方法在中继处的处理相对更简单。
1 信道模型
我们假设2个发送机要将自己的保密消息发送给对应的期望接收机,而不希望被非期望接收机窃听到自己的保密消息,因此,对于接收机1,要能够解码出发送机1的信号而不能解码出发送机2的信号;对于接收机2,要能解码出发送机2的信号而不能解码出发送机1的信号。当发送机和接收机间的信道较差时,采用中继传输可有效改善传输性能。本文研究,2对收发机间通过1个中继进行信号转发的情况,收发机间存在直接链路。系统模型如图1所示。
中继R采用放大转发模式,放大倍数为r。中继除转发信号外,同时还发送协作干扰信号XR。中继接收信号YR和接收机1,2的接收信号Y1,Y2分别为
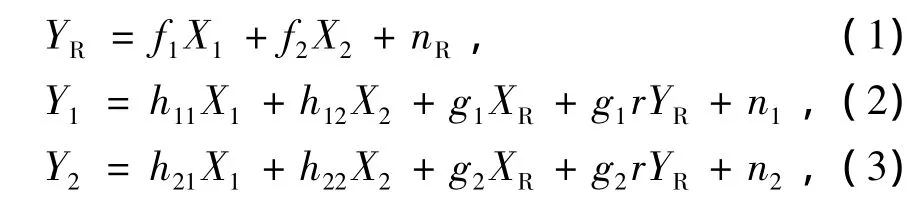
将YR代入(2)式,(3)式中,得

(1)-(5)式中:X1,X2分别是发送机1,2的发送信号;nR,n1,n2分别是中继、接收机1、接收机2的噪声,都是均值为0,方差为1的高斯白噪声;hji(i,j=1,2)是第i个发送端到第j个接收端的直达链路信道增益;fi(i=1,2)是第i个发送端到中继的信道增益;gi(i=1,2)是中继到第i个接收端的信道增益。所有的信道输入满足功率约束E[X2i]≤P,E[X2R]≤P,P为发送信号的功率。每个发送机i希望将消息Wi发送给期望接收端i,而对其他的接收端都保密。
发送机1的消息W1从集合w1中等概率随机选择,消息发送速率为R1≜log|w1|,其中n是使用信道的数量,·||表示集合的大小。发送机1采用随机编码函数f1∶w1→X1来对W1进行编码,X1≜X1n为用户1的发送信号,长度为n。同样,发送机2的消息W2从集合w2中等概率随机选择,消息发送速率为,采用随机编码函数f2∶w2→X2来对W2进行编码得到发送信号X2≜X2n。消息信号对非期望接收端都是保密的,即每个接收端对其他接收端来说相当于窃听者。接收机i希望从收到的信号Yi中解码出消息。如果接收端的解码错误率不大于任意小的正数ε,用公式表示为
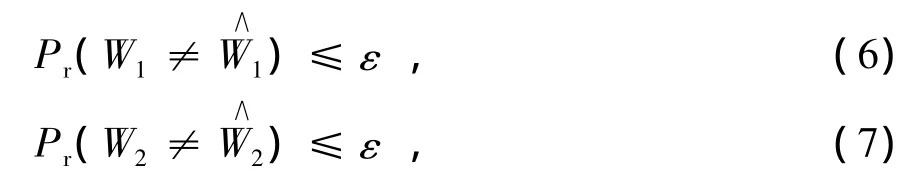
即接收端能可靠解码该消息,我们就称系统可达到保密速率对(R1,R2),(6)式中,Pr(·)表示概率。
同时,对窃听端而言要保证信息安全,必须满足

(8)式中:H(Wi)表示Wi的信息熵;H(W1|Y2)表示已知Y2的条件下W1的条件熵。(8)-(9)式表明在窃听端接收到信号Yi的情况下,保密消息Wj,j≠i的不确定度几乎等于该消息本身的信息熵。
总的安全自由度为

(10)式中,sup表示对所有可实现的保密速率对(R1,R2)的上确界。
对于系统的安全性能分析时,有很多种衡量指标。与文献[8-9]类似,本文也采用保密速率和安全自由度来衡量系统的安全性能。
2 安全自由度分析
本文中假设信道系数为实数,实干扰对齐技术多用于实信道系数的情况来提升系统的安全自由度。若信道系数为复数[9],可以将复数的实部和虚部分别采用实干扰对齐技术来处理。本文的方案中,中继端放大转发,同时发送协作干扰信号,然后采用实干扰对齐技术,并分析得出系统的总安全自由度。
2.1 实干扰对齐简介
引理1[4]如果 a1,a2,…,aL为有理数,q1,q2,…,qL为非零实数,当且仅当a1=a2=… =aL=0时,等式a1q1+a2q2+… +aLqL=0成立,则称q1,q2,…,qL有理独立,且有理维度为L。
实干扰对齐[10-11]多用于实信道系数的系统。这种系统中的有理数对应多天线系统中的矢量,有理数的有理维度[9]对应多天线系统中的矢量维度,并且在接收端系数有理独立的各个分量是可区分开的。
对于点对点的标量信道

(11)式中:x是信道输入信号且满足功率限制E[x2]≤P;z为加性高斯白噪声,满足均值为0,方差为σ2的正态分布,即z~N(0,σ2)。由于讨论的是标量信道,信道系数都为实数,因此,采用PAM调制。假设信道输入符号来自如下的PAM星座

(12)式中:Q是一个正整数;a是为了使传输功率标准化的一个实数,同时也是该PAM星座信号点之间的最小距离,即该星座最小距离dmin=a。采用该星座进行调制时,在方差为σ2的高斯白噪声条件下,接收符号的错误率有如下上界[4-5]

由于该星座中有2Q+1个信号点,该PAM方案的信息发送速率为R=log(2Q+1)。对任意足够小的δ>0,我们选择和,其中,γ是与P独立的常数,则有
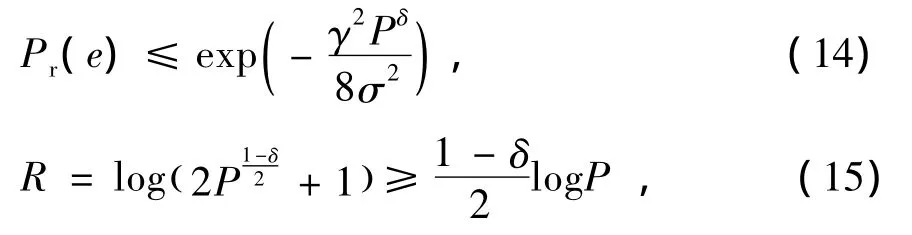
上述点对点标量信道的PAM方案可以推广到多个数据流的情况。若发送信号为

则x是L个独立数据流bi的合成信号,E[x2]≤P。其中,q1,q2,…,qL是有理独立的实数,bi取自相同的PAM星座C(a,Q),且相互独立。该合成信号星座中包含(2Q+1)L个信号点。通过使用数论中Diophantine approximation的Khintchine-Groshev定理,经过计算[10-11]可知该星座中信号点的最小距离满足:对任意的δ>0,存在一个常数kδ,使得

(17)式对几乎所有有理独立的{qi}Li=1都成立,除了Lebesgue测度为0的一部分。由于根据星座的最小距离可得到的错误率是上界,故选择合适的a和Q得到足够小的最小距离,能使错误率达到任意小,速率R逼近logP。对a和Q可作如下选择[10-11]:对任意足够小的δ>0,存在一个与功率P独立的正常数γ,我们选择
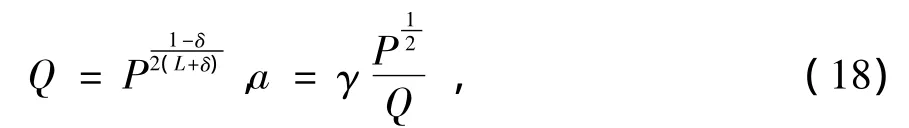
满足平均功率限制,即E[x2]≤P,对几乎所有有理独立的{qi}Li=1都成立,除了Lebesgue测度为0的一部分。
对上面结果进行扩展,如果bi独立地取自不同的星座Ci(a,Qi),则(17)式变化为
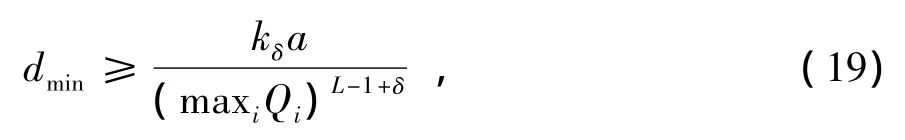
2.2 安全自由度分析
假设V1,V2,U是3个相互独立的离散随机变量,每一个变量都独立地取自相同的 PAM星座C(a,Q)。这里V1是发送端1携带消息W1的信号,V2是发送端2携带消息W2的信号,U是中继处发送的协作干扰信号,此信号不携带任何有用信息。显然有
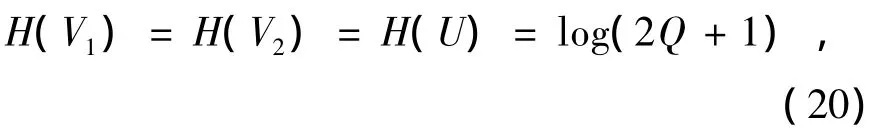
根据信道情况对V1,V2,U进行预处理,得到信道的输入信号为
预处理的目的是:在接收端1,将V2与U对齐;在接收端2,将V1与U对齐,如图2所示。

图2 两用户中继辅助干扰信道干扰对齐图解Fig.2 Illustration of interference alignment for two-user relay-assisted interference channel
此时,接收端接收到的信号为
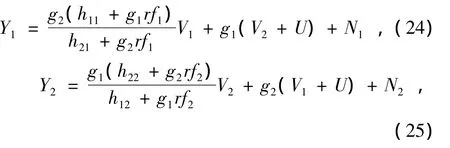
(24)—(25)式中:N1=g1rnR+n1;N2=g2rnR+n2。接收信号包含3个数据流。
为说明接收端接收到的几个数据流之间的关系,先给出2个引理。
引理2[11]如果接收信号中2个数据流前的系数一样,则称将这2个数据流对齐在同一维度中,且所占用维度与单个数据流所占维度相同。
引理3[11](数据流可分离条件)如果接收信号中各个数据流前的系数是有理独立的,则接收端可以分离这些数据流。
由引理2和引理3可知,在接收端1,V2与U对齐,并且与g1是有理独立的,接收端1可以将V1与(V2+U)分离,故接收端1可以解码V1而不能解码V2,达到了对发送端2发送信号的保密效果。
由于U是与V1,V2独立同分布的序列,由信息论可知保密速率[12]如下

(26)-(27)式中:I(V1;Y1)表示2个变量V1,Y1的互信息量;I(V1;Y2|V2)表示在已知V2的情况下,2个变量V1,Y2的互信息量。对于接收机1,V2与U对齐,与g1有理独立,故接收信号相当于2个独立数据流的合成信号,V1取自星座C(a,Q),(V2+U)取自星座 C(a,2Q),所以由(19)式可知接收端1接收星座中信号点的最小距离满足:对任意的δ>0,存在一个常数kδ,使得

接收端1在加性高斯白噪声条件下PAM调制的错误率上界为


是一个为了使输入信号的平均功率标准化的常数,且与P独立。然后有
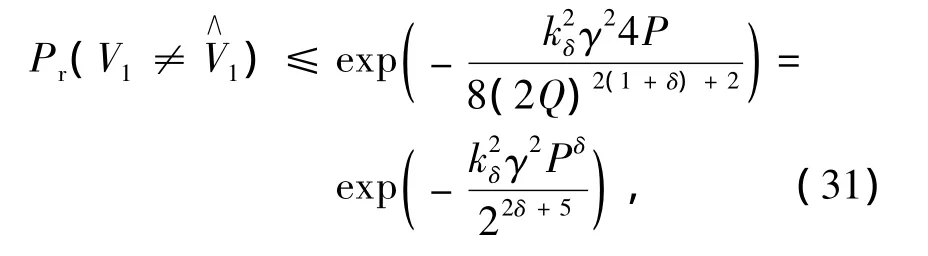

因此,V1,Y1的互信息量为
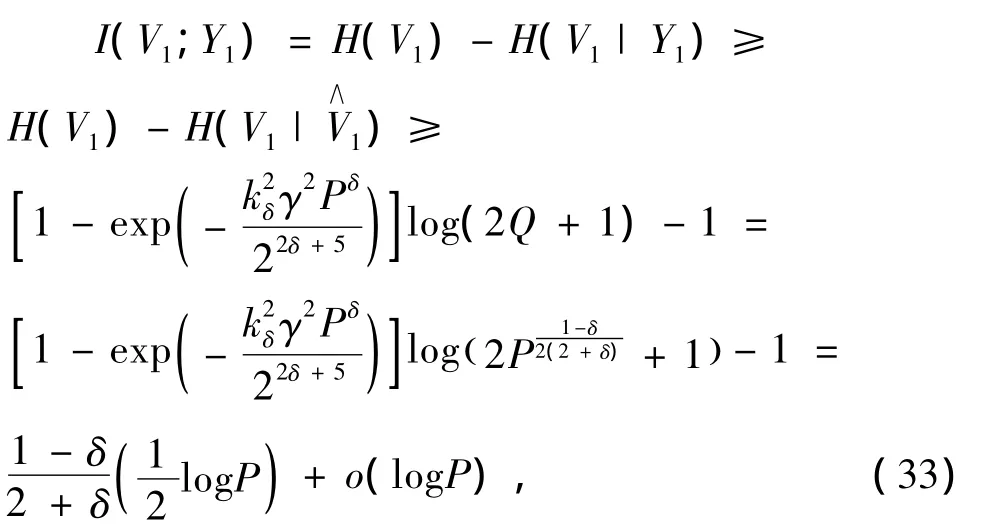
V1,Y1的条件互信息量为

收发对1的保密速率为
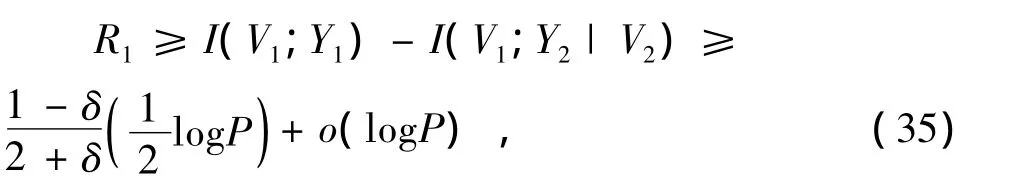
(35)式中,o(logP)表示logP的高阶无穷小。
类似,收发对2的保密速率为
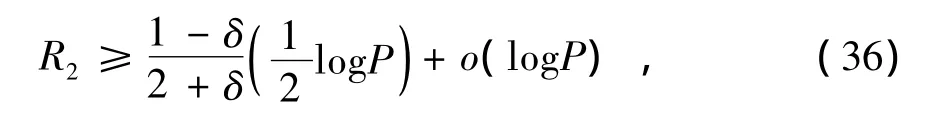
总的保密速率为
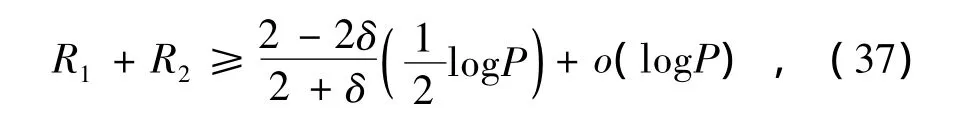
安全自由度为

两用户中继辅助干扰信道中,中继端放大转发的同时发送一个协作干扰信号,通过实干扰对齐和协作干扰信号的方法,得到总的安全自由度为1。
3 总结
本文从信息安全的角度研究了两用户中继辅助干扰信道的保密通信问题,旨在针对源端与目的端有直接链路的两用户中继辅助信道模型。该模型中的中继端除了有放大转发的功能外,还同时发送一个协作干扰信号,然后设计实干扰对齐方案,分析得出系统的总安全自由度为1。我们需要仔细选择携带保密消息的信号和用于协作干扰的信号,还需要仔细选择PAM星座中的相关参数,这样才能在接收端达到完美对齐,使接收端能够解码期望信息而不能解码非期望信息,实现对发送信号的真正保密。与文献[8]相比,两用户干扰信道无中继条件下的安全自由度为2/3,本文通过中继辅助的方法增加了安全自由度。与文献[9]中的方法相比,虽然得到的安全自由度相等,但是本文的方法不需要利用中继将X信道转化为Z信道,简化了中继的处理过程。
[1]HE X,YENER A.K-user interference channels:Achievable secrecy rate and degrees of freedom[C]//IEEE.IEEE Information Theory Workshop on Networking and Information Theory.Volos:IEEE Press,2009:336-340.
[2]KOYLUOGLU O O,EL Gamal H,LIFENG Lai,et al.Interference Alignment for Secrecy[J].IEEE Transactions on Information Theory,2011,57(6):3323-3332.
[3]CADAMBE V R,JAFER S A.Interference Alignment and Degrees of Freedom of the K-User Interference Channel[J].IEEE Transactions on Information Theory,2008,54(8):3425-3441.
[4]XIE Jianwei,ULUKUS Sennur.Real interference alignment for the K-user Gaussian interference compound wiretap channel[C]//IEEE.2010 48th Annual Allerton Conference on Communication,Control and Computing.Allerton,IL:IEEE Press,2010:1252-1257.
[5]XIE Jianwei,ULUKUS Sennur.Unified secure DoF analysis of K-User Gaussian interference channels[C]//IEEE.2013 IEEE International Symposium on Information Theory Proceedings(ISIT).Istanbul,IL:IEEE Press,2013:1107-1111.
[6]XIE Jianwei,ULUKUS Sennur.Secure degrees of freedom of the Gaussian wiretap channel with helpers[C]//IEEE.2012 50th Annual Allerton Conference on Communication,Control and Computing.Monticello,IL:IEEE Press,2012:193-200.
[7]XIE Jianwei,ULUKUS Sennur.Secure degrees of freedom of the Gaussian wiretap channel with helpers and no eavesdropper CSI:Blind cooperative jamming[C]//IEEE.2013 47th Annual Conference on Information Sciences and Systems(CISS).Baltimore,MD:IEEE Press,2013:1-5.
[8]XIE Jianwei,ULUKUS Sennur.Secure degrees of freedom of one-hop wireless networks[J].IEEE Transactions on Information Theory,2014,60(6):3359-3378.
[9]HO Z,JORSWIECK E.Secure degrees of freedom on widely linearinstantaneous relay-assisted interference channel[C]//IEEE.2013 IEEE 14th Workshop on Signal Processing Advances in Wireless Communications(SPAWC).Darmstadt:IEEE Press,2013:684-688.
[10]MOTAHARI A S,GHARAN S O,KHANDANI A K.Real interference alignment with real numbers[EB/OL].(2009-08-12) [2013-09-22].http://arxiv.org/abs/0908.1208.
[11]MOTAHARI A S,GHARAN S O,MADDAH Ali M A,et al.Real interference alignment:Exploiting the potential of single antenna systems[EB/OL].(2009-11-18) [2013-10-10].http://arxiv.org/abs/0908.2282.
[12]LIU Ruoheng,MARIC I,SPASOJEVIC P,et al.Discrete memoryless interference and broadcast channels with confidential messages:secrecy rate regions[J].IEEE Transactions on Information Theory,2008,54(6):2493-2507.
