高职数学教学中融入专业案例的探索

2014-12-11葛志利

江苏科技信息 2014年23期

葛志利

（南京化工职业技术学院基础部，江苏南京 210048）

1 现有的高职数学教学现状

数学教育本质上是一种数学素质教育。从小学到中学，学生们一直在学习数学。数学给大家留下的印象是难。尤其是针对高职生源，普遍存在着畏难情绪。他们对数学的认识也停留在反复做题，对数学的应用性缺乏新的认识，他们认为数学是无用的，跟他们的专业没有关系。针对这一情况，作为教师不能再像以前一样停留在传统的教学方法上。而是要努力改变这一现状，激发学生学习数学的兴趣。近年来，各大高职院校在高职数学教学改革方面也做了很多努力，但由于课时有限，以及与专业需求之间依然缺乏有效的衔接，并未使数学在整个人才培养过程中起到垫脚石的作用。为此，我们有必要将专业案例融入到高职数学课程中来，真正做到数学的服务性。

2 专业案例含义

专业案例是指运用高职学生能够接受的、需要掌握的、最基本的数学知识所能够解决的、按学生所学专业分类的、出现在后继专业课程中的典型案例。因此专业案例的特征是针对专业遴选的应用性和贴近学生基础的简单性。它是面向专业的建模案例，但是又不同于建模案例。传统的建模案例一般来自实际工程与经济管理，信息量大，所需数学知识多。主要是针对参加建模竞赛的优秀学生，不适合普遍教学。而专业案例更贴近高职学生基础，从他们所学的专业出发，在其能够接受的范围内选用数学知识展开数学建模，在分析和解决与其相关的专业问题中获得成就感，让他们感受到数学实实在在地就在身边，并为其掌握专业技能铺下基石，从而使其学习数学的积极性得到最大化的调动。

2.1 2 个具体实例

2.1.1 实例1：导数概念中专业案例融入

导数定义可以通过瞬时速度和切线斜率的共性抽象出来的函数变化率给出。除此之外，导数概念与经济学的边际函数、弹性以及化学中的物质衰变等实际问题有密切关系。我们通过引入经济管理中的质量成本优化分析模型来说明其概念和应用。

2.1.2 问题提出：质量成本优化分析

所谓质量成本是指企业为了保持和达到规定的质量水平所需的费用。它包括：（1）符合性成本，用于预防不合格品和故障等所需的费用及评定质量的费用；（2）非符合性成本，在产品出厂前后由于未满足规定的质量需求而支付的费用。通常符合性成本越高，产品质量的符合性越好，不合格品率越低，相应的非符合性成本越低。

2.1.3 模型建立与分析

设产品不合格率为P，符合性成本为C1，非符合性成本为C2，总成本为C，则有设F 为每件不合格产品所消耗费用，则有C2=F·P。

将P*带入总成本C 公式，得到

2.1.4 教学效果评价

该案例的引入加深学生对导数概念的理解，并体会导数在经济管理中的应用价值。从提出问题到解决问题，学生积极参与整个教学过程，增强他们学习兴趣，极大提高了教学效果。

2.2.1 实例2：微分方程概念中专业案例融入

微分方程是由于生产实践中某些问题的需要，伴随着微积分发展起来的一门学科。在科学研究和实际生产中，很多问题都可以归结为用微分方程表示的数学模型。我们通过对企业管理中常见的固定资产折旧分析来说明其在经济中的应用。

2.2.2 问题提出：固定资产折旧分析

假定某固定资产5 年前购买时资产的价格是10000 元，而现在的价值是6000 元，那么再过10 年后该固定资产的价值时多少呢？（一般说来，固定资产在任一单位时刻的折旧额与当时固定资产的价值都是成正比的）。

2.2.3 模型建立与分析

首先我们可以假设t 时刻该固定资产的价值为P=P（t），则在［t，t+Δt］这段时间内该固定资产单位时刻的折旧额可表示为由题意可得：

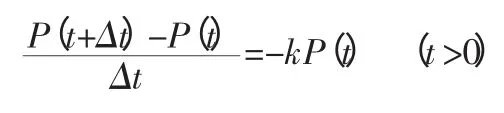
令Δt→0，即得：

不难求出该方程的通解是P（t）=Ce-kt。

为方便计算，记5 年前的时刻t=0，于是有初始条件P（0）=10000，带入通解得到C=10000，所以，原方程的特解解为P（t）=10000e-kt。

为确定比例系数k，可将P（5）=6000 代入上式，得到，从而有，这就是价值P 与时间t 之间的关系。于是，得到再过10 年后价值为：

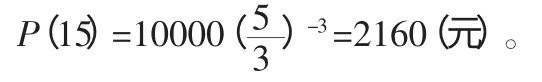
2.2.4 教学效果评价

固定资产折旧是企业进行成本核算时必须要计算的一个指标。因此，该案例在企业管理领域有很强的应用价值。学生通过对实际问题的建模解决过程加深了对微分方程概念的理解，掌握了该问题的解决方法，体验到数学来源于实际生活，从而激发学生的学习兴趣，培养学生的创新意识，提高整个课堂的教学质量。

3 在实施专业案例教学时应注意的问题

首先，我们在选择专业案例时要注意严格控制案例的难度，它不能和传统的建模案例相一致。要充分考虑到学生的接受程度。在合适的教学情境下引入案例，激发他们的求知欲和找到学习数学的成就感。

其次，在教学过程中切忌喧宾夺主，数学课始终是数学课。我们要在不破坏整体数学知识结构的框架下引入案例，而不是讲授专业课。案例只是为教学服务的。

最后，最应该注意的是在收集案例时要围绕某一个知识点面向各个专业。在选择知识点时要优先选择基础知识点，在有限的课时情况下，我们对章节前言或是一些重要的概念上引入案例，引导他们将实际问题转化为数学问题，再用数学知识去求解问题。关注思维，淡化形式。

4 资源共享

专业案例教学是高职数学教学改革的一种思路。其得以实施并行之有效的关键点在于专业案例库的构建。案例库并非简单的案例组合，要求按照数学知识逻辑，后继专业应用需要以及学习人群等进行划分，应该是具有可操作、可更新、可共享的系统。因此，无论对于教师还是学生，都需要一个学习与选择的共享平台，案例库网络资源就是实现共享，让广大师生受益的良好渠道。

5 结语

将专业案例融入到高职数学课程是一个庞大的工程，要求数学教师改变以往的传统的教学方法，花费大量的时间精力去研究数学在专业课程中的应用。另外，案例库的开发也处于摸索阶段。这些都需要我们自身不断努力，同时也需要得到广大领导乃至学校的支持。总之，在将专业案例完美融入到高职数学课堂教学中是我们每一位任课教师追求的目标。

［1］翟步祥.高职数学课程培养体系研究［J］.教育与职业，2012（32）：131-132.

［2］荆科，康宁，姚云飞.数学建模案例在高等数学教学中的应用探讨［J］.哈尔滨师范大学自然科学学报，2013（3）：26-28.

［3］李亚芹，宗容，李海燕.以数学建模实践为平台的高等数学教学探索［J］.高等教育研究，2009（1）：89-90.