基于欧拉角分析法的电动二维转镜读数修正

王涛，王劲松，徐翔宇，陶宗慧

（1.长春理工大学 光电工程学院，长春 130022；2.长春中国光学科学技术馆，长春 130022）

电动二维转台广泛应用于跟踪、测量及仿真领域。在这些领域中，二维转台多作为发射源，或者是接收源的调整与测量工具，如激光跟踪和光电发射平台，对光学目标位置的描述多是用俯仰角与方位角［1］。

本文的二维转镜是电动二维转台在光学测量上的一种应用。在光学仪器中，二维转台用于光学调整和测量［2］，但是由于二维转镜的调整特点，出射光线的在俯仰和方位方向的走动量与二维转台方位和俯仰方位的转动角之间存在不一致的现象。本文针对电动二维转台在光学调整中存在的转角值与像移不一致的问题，利用欧拉角加以分析，并提出了一种软件修正的方法。

1 问题的提出

实际应用中二维转台多数采用力矩电机实现方位、俯仰方向的转动功能，高精度的光电编码器给出转台两轴的转角值［3］。如图1所示的二维转镜即是一个实例。本文中的二维转镜是用于轻武器红外瞄具瞄准基线变化量测量系统。在测量系统中二维转镜对光线进行调整，并对光线走动量进行测量。

二维转台包括方位和俯仰两个方向的转动，其中俯仰的转动轴是固定的，方位的转动轴方向随着俯仰轴的转动改变。其通过对平面镜进行调整进而对出射光线方向进行调整和读数。它的方位角和俯仰角是用来对平面镜的姿态进行描述。出射光线的方位角与俯仰角无法通过二维转台直接读出，其与二维转台俯仰角方位角存在函数关系。为了求出射光线的方位俯仰角，需要利用欧拉角的知识建立坐标系。

图1 转台结构示意图

2 欧拉角坐标系的建立

在测量系统中入射光线是不变的，为了求出出射光线，需要知道平面镜法线的方向向量坐标［4，5］。法线向量在动态坐标系下是不变的，需要将法线向量由动态坐标系（XYZ）转换到实验参考系（xyz）下。具有公共坐标原点和尺度的空间直角坐标系之间的坐标转换，最方便的是采用欧拉角来描述。欧拉角有多种取法，如图2所示的欧拉角αβγ就是最常见的一种［6，7］。

图2 欧拉角示意图

欧拉角是用来描述刚体在三维欧几里得空间的取向。对于任何参考系，一个刚体的取向是依照顺序，从参考系做三个欧拉角的旋转而设定的，所以刚体的取向可以用三个基本旋转矩阵来决定［8，9］。换句话说，任何关于刚体旋转的旋转矩阵是由三个基本旋转矩阵复合而成的。对于在三维空间里的一个参考系，任何坐标系的取向，都可以用三个欧拉角来表现［10，11］。参考系又称为实验室参考系，即为图中的xyz坐标系，是静止不动的，而动态坐标系则固定于刚体，即为图中的XYZ坐标系，随着刚体的旋转而旋转。

对于二维转台，俯仰轴和方位轴是正交的，两者之间成90度角。俯仰方向的转动轴对于实验室参考系来说是固定不动的，而方位转轴的方向是随着俯仰方向的转动而变化的。俯仰坐标系对应的是欧拉角坐标系中的实验室参考系，方位坐标系对应的是动态坐标系。

图3 二维转镜坐标系

根据上述分析，建立二维转镜的坐标系。该坐标系以二维转镜的圆心为原点，取方位方向的旋转轴为z轴，取俯仰方向的旋转轴为Z轴。如图3所示是建立的坐标系，图中XYZ为实验室参考系，xyz为动态坐标系。

3 旋转矩阵与出射光线矢量的推导

由二维转台两轴转动对应于欧拉角坐标系的转动得出，α为俯仰轴的转动量，γ为方位轴的转动量，β为动态坐标系相对实验室参考系转动的角度。根据欧拉角的公式，可以得到二维转台的旋转矩阵：

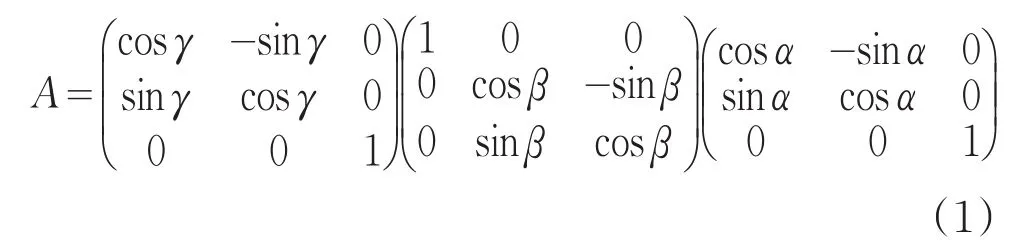
三个矩阵分别对应着三个转动［5］，分别是动态坐标系绕着实验室参考系z轴的转动的转动即俯仰轴的转动、动态坐标系的转动对应于方位轴的转动和动态坐标系相对于实验室参考系的转动。对（1）式展开，得

根据二维转台坐标系特点知道β=π/2，而且是固定不变的。根据平面光学的知识，在平面镜反射中，知道入射光线和法线就能得到出射光线。在动态坐标系xyz坐标系内取镜面的单位法向量（0，1，0），通过旋转矩阵将其转换到实验室参考系下得到法线在实验室参考系下的坐标为：

由（4）式可知，法线的坐标是关于俯仰轴的转动量γ，方位轴的转动量α的函数。

由光的反射定律知，入射光线与法线的夹角和出射光线与法线的夹角相等［3］。如图4所示，入射光线OA，法线OC，出射光线OB在同一个平面上。在实验室参考系中已知法线，入射光线单位方向向量，需要求出出射光线的坐标。入射光线的方向向量为(1 0 0)。

ϕ是小镜子的转动量，OE=cosϕ，cosϕ=。由三角形 ΔEOF 与ΔCOD相似得，CD长度是C点的纵坐标也就是法线单位向量的纵坐标，EF就是E点的纵坐标。由AE=EB和三角形相似，可知B点的纵坐标是E点纵坐标的2倍数，这样就得到了出射光线方向向量的纵坐标。

图4 出射光坐标解算示意图

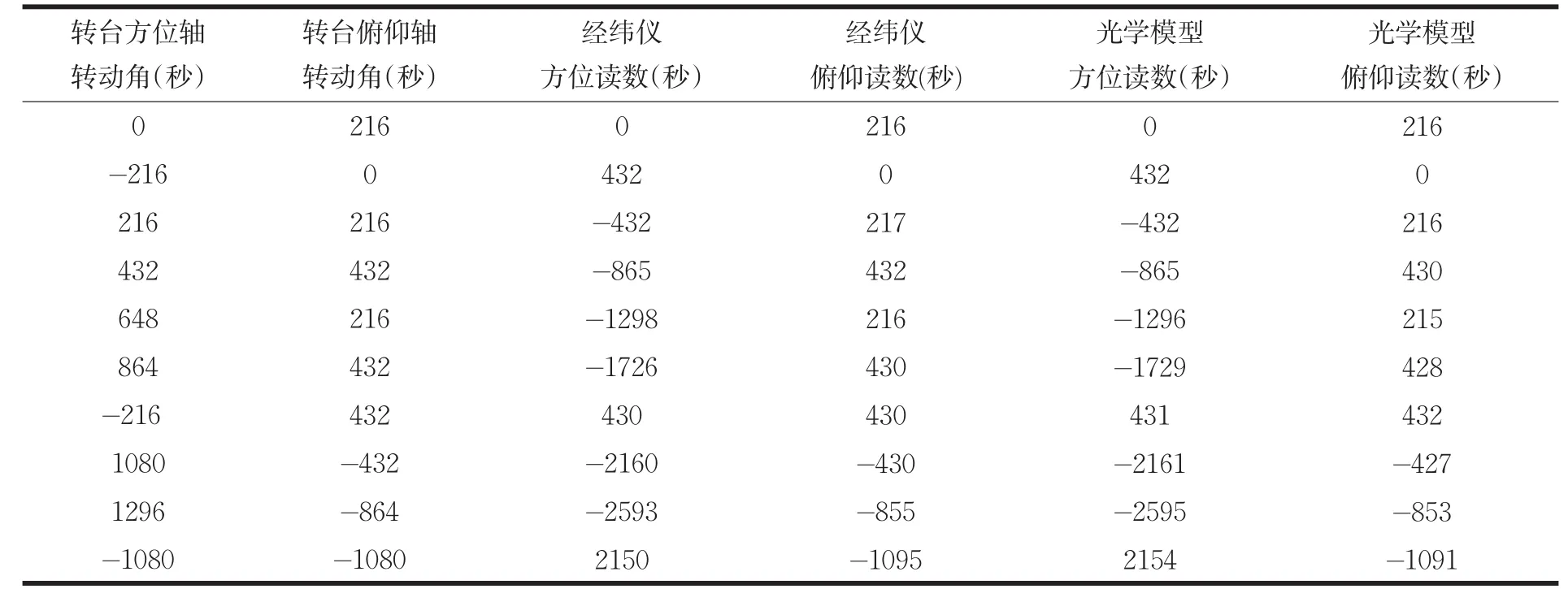
表1 与经纬仪对比测量结果表 单位：秒

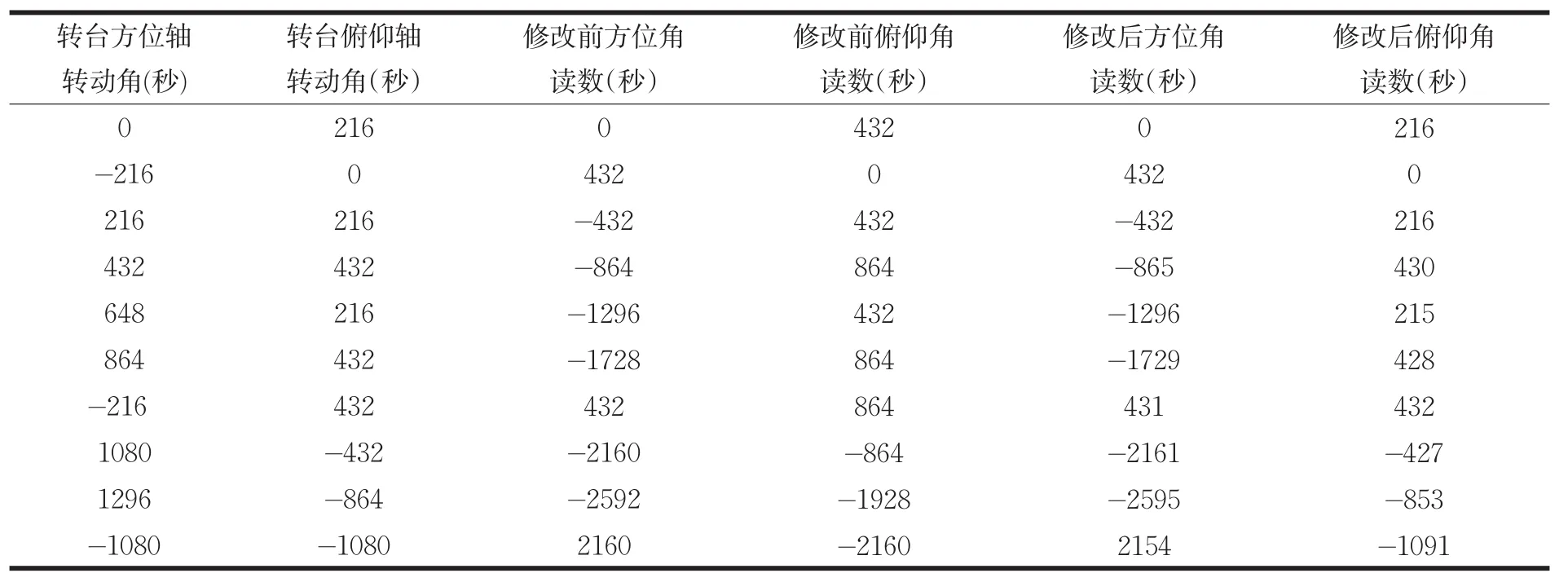
表2 修正前后读数比较 单位：秒

同样的方法可以得到B点的x坐标，y坐标，z坐标。这样就可以得到B点的坐标。

得出出射光线的单位方向向量是（2cos2γsin2α-1，sin2αsin2γ ，-cosαsin2γ）。出射光线在垂直面上的投影与水平面的夹角即出射光线俯仰角为：

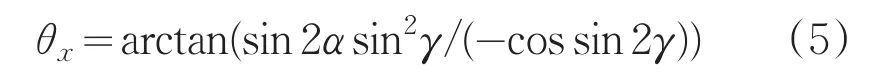
出射光线在水平面上的投影与垂直面的夹角即为出射光线方位角：

4 验证实验

为了验证上述模型的正确性，实验采用高精度经纬仪对出射光线进行测量，得到光线在方位和俯仰方向上的走动量，并与光学模型得到的数据进行对比。实验装置如图5所示。

图5 实验实物图

调节精密二维调整台的两个轴角到零位，以经纬仪对准设备的十字分划，俯仰和方位角相对为零。将经纬仪按照实验规划的空间点的位置在俯仰方位两个方向各转动相应的角度，然后调节精密转台，让设备十字分划与经纬仪再次对准，这样就获得了出射光线在方位俯仰两个方向上的角度。与修改前的读数进行对比，由表2中的数据可以看出，没修正时读数是错误的。再将其与上述模型求出的数进行对比如表1，可知光学模型得出的值与实际测量所得值之间的差值小于4秒，与分析计算吻合。

5 结论

本文对二维转镜的调整特点进行了研究，运用欧拉角的知识构建了光学模型，并进行了验证实验。此方法在不改变转台结构的情况下，解决了由于二维转镜调整特点引起的读数问题。在俯仰和方位方向上的测量精度达到4秒，符合轻武器红外瞄具瞄准基线变化量测量系统对二维转镜的精度要求。并对二维转台在其他方面应用时误差分析与修正有指导意义。

［1］刘万里，王占奎，曲兴华，等.激光跟踪测量系统跟踪转镜的误差分析［J］.光学精密工程，2008，16（4）：585-589.

［2］王劲松，安志勇，李海兰.反射式平行光管的红外瞄具零位走动量测量方法研究［J］.兵工学报，2010，31（11）：1421-1425.

［3］张西龙，孙宝玉，孙建伟，等.高精度二维转台指向误差分析［J］.长春工业大学学报，2012，33（4）：377-382.

［4］郁道银，谈恒英.工程光学［M］.北京：机械工业出版社，2006.

［5］白素平，王春艳，庞春颖.基于坐标变换的动态光学成像性质研究［J］.光子学报，2001，20（7）：846-850.

［6］XU Xu，Chang Chienchi，Gert S Faber，et al.Estimation of 3-D peak L5/S1 joint moment during asymmetric lifting tasks with cubic spline interpolation of segment Euler angles［J］.Applied Ergonomics，2011，43（1），115-120.

［7］Wong Yueshuen，Kim Wangdo，Ying Ning.Passive motion characteristics of the talocrural and the subtalar joint by dual Euler angles［J］.Journal of Biomechanics，2004，38（12）.2480-2485.

［8］肖伟，梁久祯，陈玮琪.基于四元数的3D物体旋转及运动插值［J］.系统仿真学报，2012，24（3）：624-627.

［9］金华，戴金海.坐标变换方法及在卷弧翼弹弹道仿真中的应用［J］.计算机仿真，2007，24（7）：43-46.

［10］刘忠，梁晓庚，贾晓洪，等.基于四元数的导弹反步控制及全方位算法应用［J］.系统仿真学报，2006，18（10）：2734-2737.

［11］赵彦，张新锋，施浒立.基于四元数的射电望远镜指向误差分析方法［J］.机械科学与技术，2009，28（10）：1359-1363.