一种基于模板匹配的远场畸变校正方法

黄殿君，景文博，王晓曼，刘学

（长春理工大学 电子信息工程学院，长春 130022）

激光照射性能监测系统工作时，受主光轴入射角度、相对位移等因素影响，采集目标过程中会产生较严重的图像畸变，影响激光照射器性能评估。

针对图像畸变校正，国内外已有很多学者进行研究。Wang［1］、Lucchese［2］等人提出了同时校正倾斜畸变和径向畸变的方法，但需要引入5次多项式的径向畸变模型，大大增加了算法的复杂度，降低执行速度；解凯［3］等人利用仿射非线性变换矩阵进行镜头畸变校正，但由于非线性矩阵初值不易确定，可能引起较大的误差；肖志涛［4］等人利用Hough变换检测目标边缘进行畸变校正，然而在目标背景复杂、目标边缘不清晰的情况下，很难构造出通用的边缘检测算子。而激光照射性能监测系统中，由于采用高分辨率CCD图像传感器、实验背景复杂、受测量环境影响严重，故以上算法均不能满足本系统需求。

针对以上问题，本文提出一种基于模板匹配的远场畸变校正方法，利用模板匹配算法识别畸变靶板角点，降低了复杂背景对畸变校正的影响。仅需相机主光轴相对靶板的入射角度，通过相机成像模型和透视投影变换求解畸变校正系数，即可完成对图像的畸变校正。该方法克服了传统校正方法对图像清晰度要求苛刻、校正精度低、效果差等缺点，具有实验条件要求低、处理速度快、校正结果精确等优点。

1 激光照射性能监测系统

图1为激光照射性能监测系统示意图，相机安置于距轨道LKm处的转台，靶板与地面法线存在夹角α，并沿轨道按一定的速度v移动，转台在跟踪系统的控制下转动跟踪靶板，实现对靶板的连续采集。靶板的移动会造成相机主光轴相对靶板入射角度β时刻变化，而相机只能在垂直于主光轴的CCD光敏面上成像，因物平面上各处物距不同，导致各处的放大倍率也不尽相同，这就造成原本是标准矩形的靶板在图像中呈现出一个不规则的四边形。随着靶板的移动、角度的增加，图像畸变就越发严重，不能保证后续计算命中率精度等参数的准确性。

图1 激光照射性能监测系统示意图

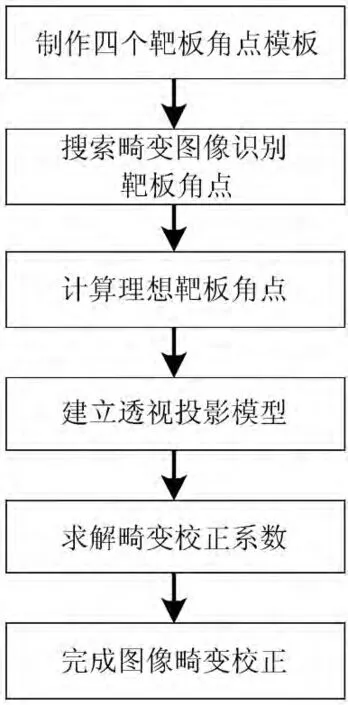
图2 畸变校正方法框图

针对激光照射性能监测系统，本文提出了一种基于模板匹配的远场畸变校正方法，框图如图2所示。

2 基于模板匹配的靶板角点检测

如图3所示，模板w(x,y)的大小为J×K，待搜索图像g(x,y)的大小为W×H，同时满足J≤W且K≤H 。w(x,y)和 g(x,y)相关系数公式［5］为：

其中，x=0,1,…,W-1，y=0,1,…,H-1，wˉ是w中像素的平均值，gˉ是g中与w当前所在位置相重合区域的平均值。

图3 模板匹配原理示意图

利用模板匹配可以实现对靶板角点的跟踪，图4为模板匹配法跟踪识别靶板角点示意图，具体步骤如下：

图4 模板匹配法跟踪识别靶板角点示意图

（1）首先选择一幅靶板图像G，手动选择靶板的四个角点，分别制作角点模板w1、w2、w3和w4；

（2）通过靶板四个角点坐标计算靶心C；

（3）针对下一帧采集到的畸变靶板图像G1，以前一帧靶板图像G的模板中心为基准将模板区域扩大n倍记为g1、g2、g3和g4，每个区域作为对应靶板角点模板的待搜索区域；

（4）在区域g1移动角点模板w1，找到相关系数γ最大的位置，即可匹配出靶板角点的位置P1，同理可求出靶板另外三个角点，分别记为P2、P3和P4。

3 理想靶板角点坐标

根据图1所示，随着靶板的移动，可计算得出相机距靶板的距离为Lt=L/sinβ；已知靶板的实际宽高为Wt×Ht，由于物距远远大于光学系统焦距f，故可利用小孔成像模型，计算靶板在图像中的尺寸

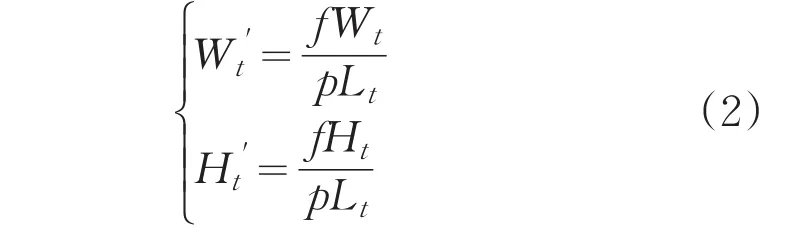
其中，f为光学系统焦距，p为相机像元尺寸。

实际靶板为一个标准的矩形，因此校正后的靶板也应该为一个标准矩形，只是实际靶板的大小在图像中以像素的形式表现出来。

通过以上分析可求出畸变图像经校正后理想靶板四个角点的相对位置坐标，由于本系统中只关心靶板的相对形态，靶板在图像中的绝对位置并不影响校正结果的，因此可以始终以前一帧图像的靶板中心作为当前帧图像的靶板中心，计算求出靶板角点坐标分别记为

4 透视投影变换

4.1 透视投影变换模型

实际物体属于三维空间的范畴，而计算机只能在二维屏幕上显示三维物体，透视投影实现了物体从三维空间到二维屏幕的变换。图5为透视投影模型示意图，平面S2为二维屏幕平面，点P(X,Y,Z)为实际物体上的一点，经透视投影变换后该点在二维屏幕平面S2上的像点为P′(x,y)。由图5可知透视变换的坐标关系为：

其中，f为光学系统焦距O2O3。

任意 t′时刻的点 (X′,Y′,Z′)，都可以利用旋转矩阵R、平移向量T和t时刻的对应点(X,Y,Z)表述［6］：

将式（3）带入上式整理得：

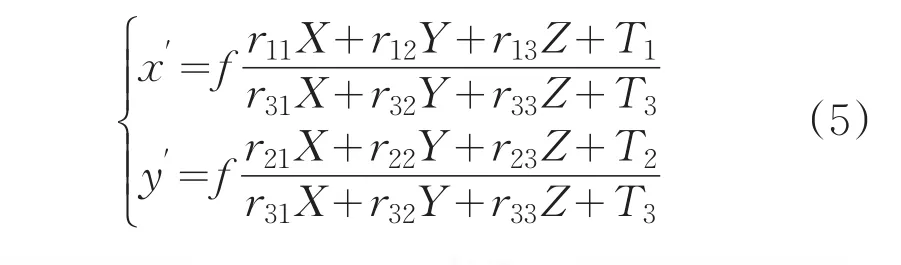
图5 透视投影模型示意图

由于成像系统焦距是一个常数，因此不失一般性，可取 f=1，即规范化透视投影。将式（5）分子分母同时除以Z，整理有：

其中，(x′,y′)为正视情况下的像素坐标，(x,y)为畸变图像中的像素坐标。

由上可知，a1至a8实际上是由旋转矩阵R、平移向量T各元素组合而成的畸变校正系数，正视图像反映了一个真实的靶板信息，式（6）建立了畸变图像和校正图像的关系。

4.2 透视投影畸变校正的具体实现

利用式（6）和四对靶板角点，可求解出8个畸变校正系数。现将式（6）写成矩阵形式：

图6 畸变图像和校正图像效果图

将畸变靶板的四个角点P1、P2、P3和P4与对应的无畸变靶板的四个角点 P1′、P2′、P3′和 P4′代入式（7）可得：

通过式（8），求出a1至a8畸变校正系数，利用畸变校正系数，实现对整帧图像的畸变校正。

5 实验结果及分析

采用Lumenera LM135M型相机为成像设备，像元尺寸为 4.75μm×4.75μm ，焦距为70mm，图像分辨率为1392×1040。

模拟激光照射性能监测系统实际测量环境进行试验：保持靶板与地面法线夹角为15°，并沿轨道移动，相机距轨道的垂直距离为100m，固定相机位置不变，随靶板移动转动相机跟踪靶板，连续采集30帧图像。在第一帧图像上，手动制作靶板角点模板；而对于其他帧图像，通过模板匹配法，跟踪识别靶板角点坐标。

利用本文基于模板匹配的远场畸变校正方法，对畸变图像进行校正，并与传统Hough变换校正法［4］进行比较，校正后效果如图6所示。图7反映了经两种方法畸变校正后的靶板质心与理想靶板质心的偏差。

为准确评估本文提出的基于模板匹配的远场畸变校正方法，分别对比校正后靶板质心在水平、垂直方向的相对误差和最大偏差，校正单帧图像的平均耗时5个指标，评价畸变校正方法的优劣。具体实验数据对比如表1所示。

表1 两种畸变校正方法的实验对比

由图6可以看出，本文提出的基于模板匹配的远场畸变校正方法校正效果明显好于传统基于Hough变换的校正法；图7曲线表明经本文方法校正过的图像，其靶心更接近理想靶心。

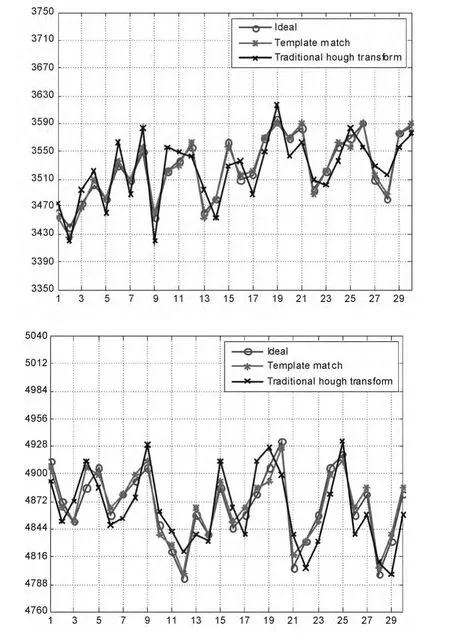
图7 两种畸变校正方法靶心偏差数据对比

由表1实验数据分析可知，基于模板匹配的远场畸变校正方法，其校正效果更好，精度更高，校正速度比传统Hough变换校正法提高了近2.6倍。

6 结论

实验表明，采用本文提出的基于模板匹配的远场畸变校正方法，可全面准确的反映出真实图像信息。本法不仅对图像质量没有特殊要求，而且操作简单，具有实验条件低、校正效果理想、结果精确、处理速度快等优点，在激光照射性能监测系统中具有重要意义。

［1］Wang X，Klette R，Rosenhahn B.Geometric and pho

to–metric correction of projected rectangular pictures［C］.In：Proceedings of International Conference on ImageandVisionComputing（IVCNZ）.Dunedin，New Zealand，2005：223-228.

［2］LucaLucchese，SanjitK Mitra.Correction of geometric lens distortion through image warping［C］.In：Proceedings of the 3rd International Symposium on Image and Signal Processing and Analysis.Rome，Italy，2003：516-521.

［3］解凯，郭恒业，张田文.一种具有径向畸变校正的图像整合算法［J］.电子学报，2004，32（10）：1726-1729.

［4］肖志涛，国澄明，孟翔宇.基于Hough变换的倾斜文本图像的检测［J］.红外与激光，2002，31（4）：315-317.

［5］唐琎，李青.一种快速的模板匹配算法［J］.计算机应用，2010，30（6）：1559-1564.

［6］Tekalp A M.Digital Video Processing［M］.北京：清华大学出版社，1998：165-166.