一种基于带宽调度的网络拥塞控制策略

孙洪涛，吴敬，李娅，秦朋

(1.山东外国语职业学院信息工程学院，山东日照276826;2.沈阳志成电子工程有限公司，辽宁沈阳110000)

随着计算机和通信技术的飞速发展，控制系统的规模越来越庞大，分散化程度越来越高，传统的点对点控制已经无法满足复杂工程系统对控制系统结构的要求。通过网络形成闭环的控制系统称为网络控制系统(networked control system，NCS)［1－2］。NCS将闭环控制回路分散于实时网络上，突破了传统控制系统在空间物理位置上的限制以及信息的封闭和局限性，已成为现代大规模复杂控制系统的首选构架，是目前国际控制领域的研究热点。

由于网络本身的固有特性，网络的引入也给控制系统分析和综合带来很多新问题［3］，如网络带宽资源的有限性、网络中信息传输的速率与传输中的延迟、信息的量化以及分布式的控制方式等。NCS由通讯网络和控制系统组成，有限的网络带宽始终是其瓶颈问题。在分析和设计网络控制系统时，必须综合考虑通讯网络与控制系统的耦合，进行控制与调度协同设计，以期同时保证控制系统品质(quality of performance，QoP)和网络服务质量(quality of service，QoS)。NCS中控制与调度的协同设计已被越来越多的学者所关注［4］，开始人们注重控制算法的设计［5－9］，通过将时延、数据包丢失等问题融入到控制器的设计中来保证控制系统的稳定性，提高控制性能，此类控制算法将网络因素包含在控制器设计上，只是形式上的联合，并未考虑到网络的QoS。随着研究的深入，当网络中信息传输不畅导致原有的控制算法难以施行，反过来又提高了控制器设计的难度时，催生了注重于网络资源分配的调度策略，通过带宽分配及采样周期的调整不仅提高了QoS，而且从侧面提高了控制算法执行的有效性，从而达到真正意义上的NCS协同设计［10－14］。综上所述，较好的网络服务质量是保证控制系统品质的前提。因此，在保证控制系统QoP的前提下，有必要对NCS中的网络进行进一步的研究［15－16］，在有限的网络资源下提高其综合性能。

从通讯网络角度来看，NCS中的时延、数据丢包等问题归根结底是因不同控制回路的带宽受限造成的信息不能及时传输或传输不畅，进而导致了控制器的数据无法及时更新，降低了控制系统的控制性能。通常，若用网络拥塞程度来表征数据通道中的传输状态，可以得出控制回路中的网络拥塞程度与带宽密切相关。针对因网络服务质量引起的网络控制系统综合性能的下降，本文建立了基于网络拥塞和带宽之间的线性时不变模型，通过最优的动态带宽分配实现对网络拥塞的实时控制，从而保证网络处于一个较为稳定的运行状态，降低QoS对控制系统性能的影响。

1 问题描述

考虑如图1所示的NCS。在该系统中，各个控制回路在执行控制功能时都需要通过网络进行信息的采集、运算及传输，在通过网络进行信息采集和传输数据时不同回路都需要占用一定的网络带宽。带宽可以用来衡量信息传输能力，较大的带宽能够在单位时间内传输较多的数据量，那么该控制回路的网络拥塞程度低，网络状态较稳定;较小的带宽在单位时间内只能传输较少的数据量，那么该控制回路的信息拥塞程度高，网络状态较不稳定。同时，网络运行状态可用网络拥塞程度来表示。在此，定义网络拥塞程度为状态xj(j=1，2，…，m)，各个控制回路带宽为bi(i=1，2，…，p)。调度器采集执行器侧的信息拥塞状态xj，对传感器侧的带宽进行分配，通过合理的带宽分配来消除网络拥塞，从而保证网络运行状态的稳定。

为建立网络拥塞状态xj与网络带宽bi的线性时不变模型，首先给出如下定义和假设:

定义1 如果没有网络拥塞的发生，则定义为网络的稳定状态(零状态);网络拥塞程度越大，网络的状态越不稳定;同时，网络没有发生拥塞时能够传输的最大数据量所占用的带宽定义为基本带宽，相应的采样周期称为基本采样周期。

定义2 若在原有稳定网络状态下控制系统面临扰动，需要更多的数据传输以达到被控对象的镇定，相比于基本带宽所能传输的数据量，需要额外传送的数据量称为额外数据量。故网络的拥塞状态可定义为在基本带宽情形下需通过网络传输的额外数据量

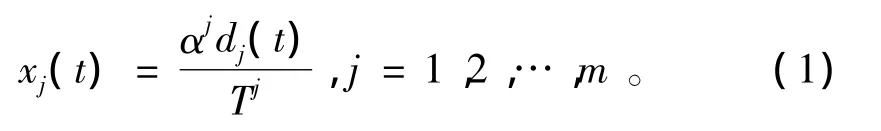
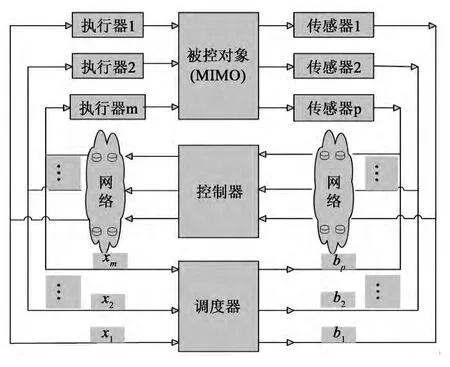
图1 含有调度器的NCS模型Fig.1 Structure of NCS containing a scheduler

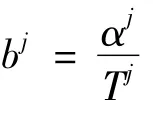
由此可见，在基本采样周期时间内，通过网络进行传输的额外数据量越大，网络拥塞就越严重，若不进行额外数据传输，则xj=0，说明信息拥塞被消除。

假设1 如果没有网络拥塞发生，则给出的控制器设计对于控制系统是有效的;并且，控制器的存在不影响网络的动态行为。

假设2 网络的拥塞状态xj和控制回路带宽bi存在如下线性关系

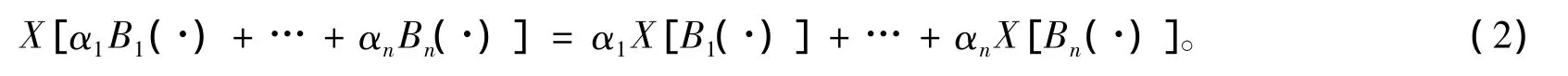
其中，X(·)，B(·)是网络拥塞状态函数和控制回路带宽函数，α1，α2，…，αn为任意有限非零常数。也就是说，网络拥塞状态xj与带宽bi满足齐次性与可加性。

基于以上定义和假设，给出如下信息拥塞状态与带宽之间的LTI模型:

其中，x= ［x1，…，xn］T∈Rn表示网络拥塞状态向量，u= ［u1，…，up］T∈Rp是含有带宽量的控制变量，A，B是适维矩阵。

本文的主要目的是通过动态的最优带宽分配来消除网络中的信息拥塞，从而提高网络的QoS。

对系统(3)，给出如下最优反馈控制器

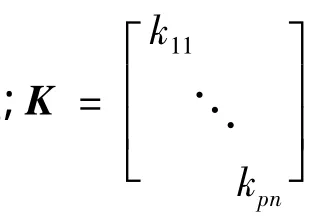
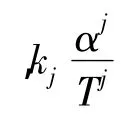
2 最优化求解方法

由上节分析可知，该问题的最优化求解是一个典型的线性二次型问题［18］。若网络产生拥塞偏离平衡状态后，希望以最优的带宽分配方式消除网络拥塞以保持网络运行的稳定状态。考虑到实际应用，应采用无限时间状态调节器，以便于实时控制。根据上述LTI模型可定义最优性能函数

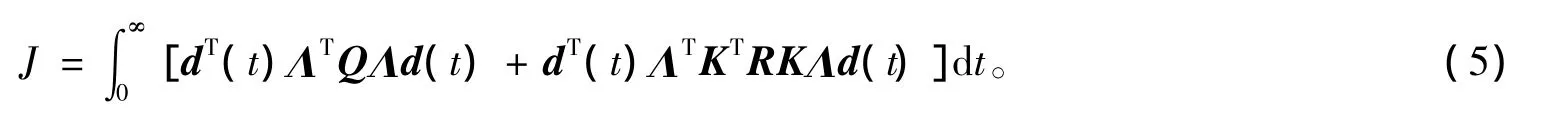
其中，Q≥0，R＞0为线性二次型权值矩阵且是适维的。

根据(5)式确定最优的带宽消耗使性能指标J达到最小。因为积分上限tf→∞，J有可能无界，为避免此类情况，故要求系统(3)可控，即秩R(A，B)=m。

引理1 对任意矩阵∑，∑∑T=Q，P是Riccati方程的解，则(A，∑)完全可观的充分必要条件是P为正定对称矩阵。

其次，我们以定理1的形式给出该问题的最优解。

定理1 若给定的阵对(A，B)可控，(A，∑)可观，则存在唯一的最优带宽控制

且最优性能指标为

其中，各个矩阵的含义同上。

最后，给出了在此最优带宽分配策略下网络运行状态的稳定性证明。

结合式(4)、(7)，则最优闭环系统可写为

其中，x(0)=x0为网络拥塞的初始状态。

上式对时间t求导可得

根据式(9)，式(11)可进一步写成

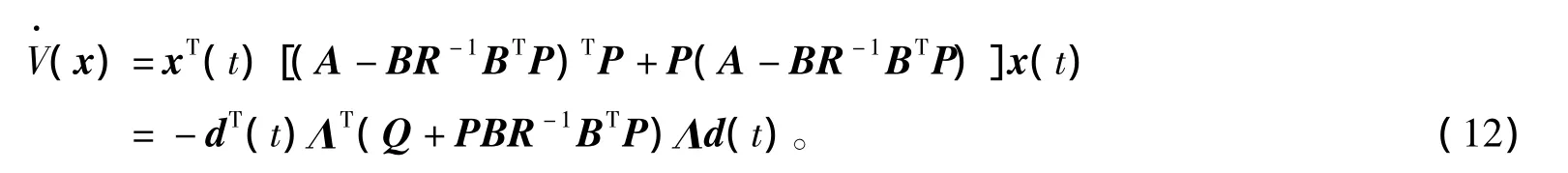
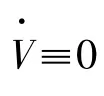
和

将式(4)代入式(14)，则

因为R＞0，所以u*T(t)=0。也就是说系统(3)只有零输入响应

将式(16)代入式(13)得

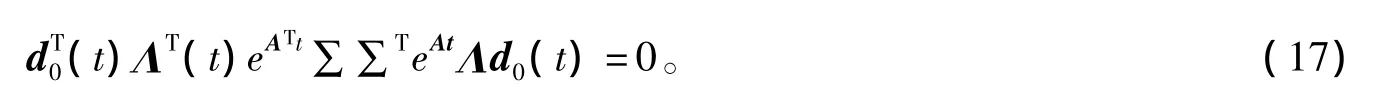
其中，∑∑T=Q。

式(17)表明

这与(A，∑)可观相矛盾。

证毕。

3 数值仿真

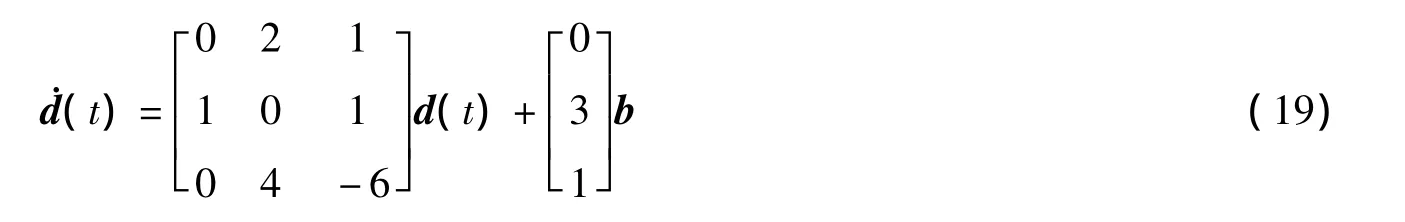
其中，d是额外数据量，b是带宽。

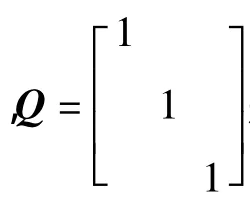
最后，通过MATLAB仿真给出了网络拥塞的状态轨迹曲线，见图2。

显然，2.7 s后信息拥塞被消除，求得最优性能指标J=2.057 1。同时，可得出带宽的实时变化曲线，见图3。

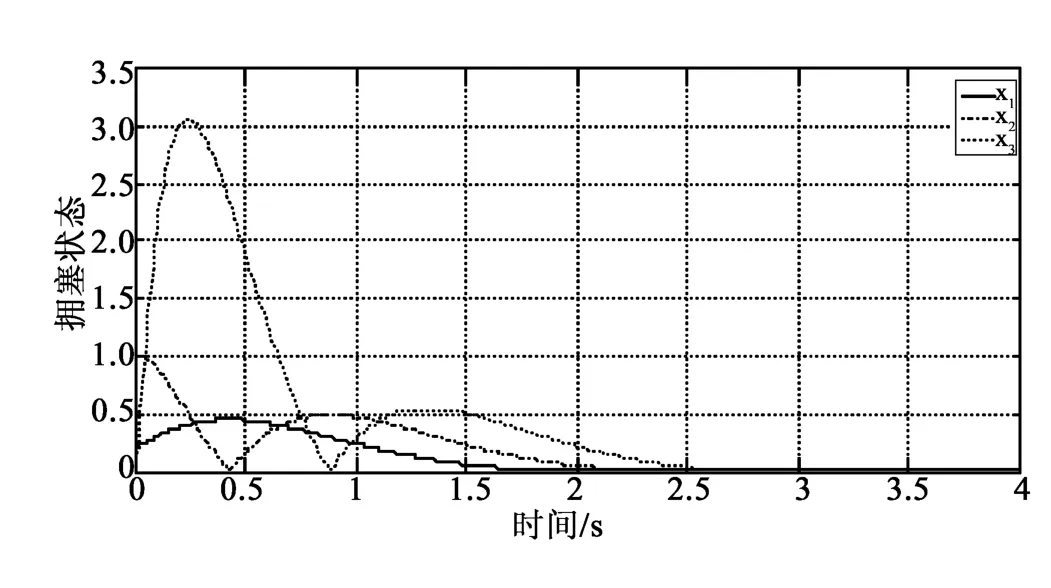
图2 信息拥塞状态变化轨迹Fig.2 Variation trajactory of network congestion state

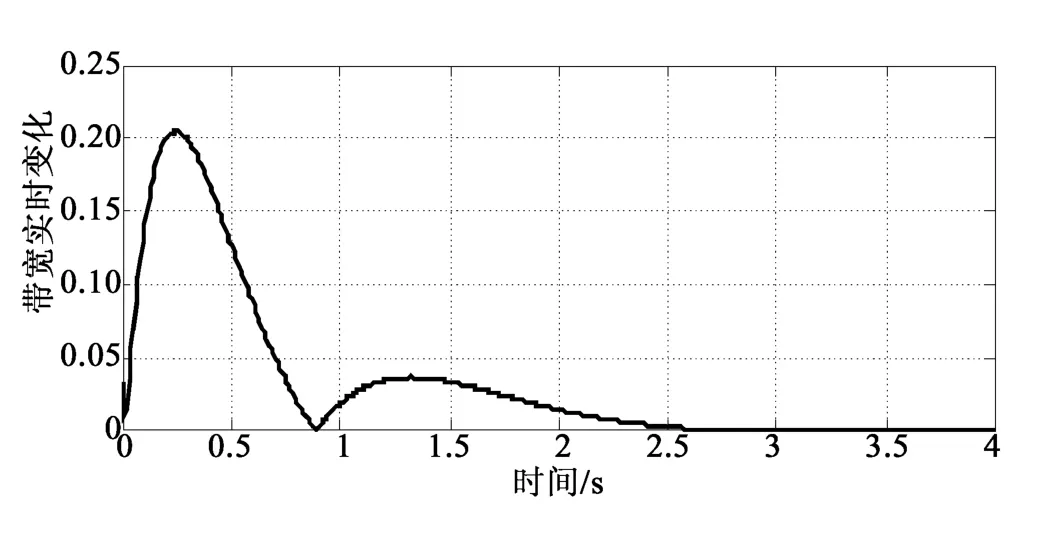
图3 带宽实时消耗曲线Fig.3 Bandwidth realtime consumption curve

本文中带宽被视为一种“能量”用来消除网络中的信息拥塞，即通过合理调整网络中带宽大小，来保证网络始终运行在一个相对稳定的状态而没有网络拥塞的发生。图2表明通过本文提出的带宽控制器设计方法能够有效消除网络拥塞，图3中的曲线则反应了带宽的实时变化，但并不意味着当网络拥塞被消除后带宽也变为零。因为当网络状态趋于稳定时，只说明各个闭环回路只是保持原有的未发生网络拥塞时基本带宽，不再需要额外的带宽，即没有额外的数据需要传输时，不需分配额外的带宽。仿真结果表明，该拥塞控制策略是有效的。

4 结语

［1］WANG Z W，GUO G.Fundamental issues and prospective directions in networked multirate control systems［J/OL］.Mathematical Problems in Engineering，2014，http://dx.doi.org/10.1155/2014/513506.

［2］BRINDHA M，MENDIRATTA J K.Networked control system-A survey［J］.International Journal of Modern Education and Computer Science，2013，5(6):42－48.

［3］游科友，谢立华.网络控制系统的最新研究综述［J］.自动化学报，2013，39(2):101－118.

［4］SETO D，LEHOCZKY J P，SHA L，et al.On task schedulability in real-time control systems［C］//17th IEEE Real-Time Systems Symposium，1996.Piscataway:IEEE，1996:13－21.

［5］BATISTA A P，JOTA F G.On the effects of time delay variations in the design of networked control system［J］.International Journal of Systems，Control and Communications，2013，5(2):120 －139.

［6］XU S J，CAI X S，GAO H.Output-feedback design of networked control systems and estimating maximum data packets dropout［C］//2013 25th Chinese Control and Decision Conference(CCDC).Piscataway:IEEE，2013:3109－3113.

［7］TORRES G，VELASCO M，MARTI P，et al.An alternative discrete-time model for networked control systems with time delay less than the sampling period［C］//39th Annual Conference of the IEEE Industrial Electronics Society，IECON 2013.Piscataway:IEEE，2013:5626－5631.

［8］GUO X L.Controller design based on variable period sampling approach for networked control systems with random delays［C］//International Conference on Networking，Sensing and Contro1，2009.Piscataway:IEEE，2009:147 －151.

［9］张宏礼，井元伟，张嗣灜.网络控制系统的主动变采样控制器设计(英)［J］.系统仿真学报，2009，21(22):7275－7280.

［10］VELASCO M，FUERTES J M，LIN C，et al.A control approach to bandwidth management in networked control system［C］//30th Annual Conference of IEEE Industrial Electronics Society，2004.Piscataway:IEEE ，2004:2343 －2348.

［11］GUO G，LU ZB，HAN Q L.Control with Markov sensors/actuators assignment［J］.IEEE Transactions on Automatic Control.2012，57(7):1799－1804.

［12］JI K，KIM W.Optimal bandwidth allocation and QoS-adaptive control co-design for networked control systems［C］//ASME 2007 International Mechanical Engineering Congress and Exposition.Washington:ASME，2007:831－839.

［13］LI Z，CHOW M Y.Adaptive multiple sampling rate scheduling of real-time networked supervisory control system-Part I［C］//32nd Annual Conference on IEEE Industrial Electronics，IECON 2006.Piscataway:IEEE，2006:4615－4620.

［14］LI Z，CHOW M Y.Sampling rate scheduling and digital filter co-design of networked supervisory Control system［C］//IEEE International Symposium on Industrial Electronics，2007.Piscataway:IEEE，2007:2893－2898.

［15］熊辉，王耀青.控制理论在拥塞控制中的应用及若干新思路［J］.武汉科技大学学报:自然科学版，2002，25(1):68－72.

［16］任敏，王万良.基于优化控制理论的网络拥塞控制方法［J］.机电工程，2003，20(5):123－126.

［17］WANG Z W，SUN H T.A Bandwidth Allocation Strategy based on the Proportion of Measurement Error in Networked Control System［C］//2012 Third International Conference on Digital Manufacturing and Automation(ICDMA).Piscataway:IEEE，2012:9－12.

［18］郑大钟.线性系统理论［M］.2版.北京:清华大学，2011:319－324.