班轮航线设计与空箱调运研究:箱种代用

张芳军，郑建风，任华玲*

(1.北京交通大学交通运输学院系统科学所，北京100044;2.北京交通大学城市交通复杂系统理论与技术教育部重点实验室，北京100044)

海洋运输(简称海运)是国际贸易中一个最主要的运输模式，其年贸易量高于80亿吨，占据世界贸易总量的65% ～85%［1］。随着货物集装箱化运输的飞速发展，班轮运输已经成为海运中最重要的运输模式，而班轮航线网络设计问题和空集装箱运输问题也就成为了海运相关研究问题中的两个重要课题。如何优化设计班轮航线、确定空集装箱的起终点，以及如何运输重箱与空箱，将直接影响班轮公司的运输成本。

在以往的很多研究中，班轮航线网络设计和空箱调运问题是两个独立的研究课题。班轮航线类似于城市交通中的公交线路，很多研究学者在班轮航线网络设计问题方面做出了很多贡献。Conley等［2］提出一个线性规划模型来研究海外到美国内陆的货物运输，其中船队包括了50艘不同类型的船。Lane等［3］研究了澳大利亚和北美西海岸之间的班轮航线设计问题，由于文中只考虑了6个港口，他们利用穷举法来选择和优化班轮航线。Rana等［4］讨论了针对既定贸易航线的集装箱班轮船队配置问题，并假设航线运营者可以放弃那些无法带来更高收益的货运需求。Jaramillo等［5］使用了线性规划方法来探讨确定班轮船队在若干已知航线上的优化配置问题，该模型的特点在于优化船队配置的同时，还考虑了航线服务频率(班期)的优化设置问题。Xie等［6］建立了一个考虑船舶折旧和船队更新因素的中长期船队规划优化模型。Fagerholt［7－8］、Sambracos等［9］和Karlaftis等［10］研究了单枢纽或中心(Hub)的班轮航线网络设计问题，即班轮从枢纽港口出发，访问几个其他港口，然后最终回到枢纽港口。该问题可以建模为一个车辆路径问题(vehicle routing problem，VRP)。Imai等［11－12］研究两个区域之间的班轮航线网络设计问题，比较分析了轮辐结构(hub-andspoke)的运输模式和multi-port-call运输模式之间的差异。

随着货物集装箱化，空箱调运问题是海运研究中的一个重要问题，同时也是一个研究热点和难点问题之一。空箱调运问题是由于各个地区的进出口贸易量的不平衡导致的。据统计，2009年亚欧的进出口贸易量［1］从亚洲到欧洲是1.15亿TEUs(twenty-foot equivalent units)，而相反方向是0.55亿TEUs，从而在亚洲积累了大量的空箱。很明显，一些地区有很多剩余的空箱，而有些地区却是欠缺空箱来装货和运货。关于空箱调运问题研究课题中的一个重要难点是，把哪些地区的剩余空箱运输到哪些欠缺空箱的地方。Crainic等［13－15］把空箱调运问题转化为一个具有能力限制的多商品流选址问题，并提出了一些精确和启发式的求解算法，包括分支定界，禁忌搜索等。Choong等［16］研究空箱租赁时间(短期或长期租赁)对空箱管理的影响，提出一个整数规划模型。Lam等［17］提出一个近似动态规划的方法来研究空箱调运问题。Dong等［18］研究班轮运输系统中船队大小和空箱调运问题，提出一个基于模拟的优化工具。Song等［19］研究班轮航线上的空箱调运，提出了两种运输策略。最近，Moon等［20］研究可折叠的集装箱和普通集装箱对空箱调运的影响。

在最近的研究中，有研究学者同时考虑班轮航线网络设计问题和空箱调运问题。Shintani等［21］提出一个两阶段模型来研究组合的班轮航线网络设计问题和空箱调运问题，并提出一个遗传算法来求解该问题。基于一个备选的班轮航线集合，Meng等［22］提出一个混合整数规划模型来求解班轮航线最优挑选和空箱分配。Song等［23］提出了一个长途班轮航线设计问题，主要包含航线设计、船队分配和空箱调运，并提出了一个三阶段的优化方法来解决此问题，以达到班轮运输成本极小化的目标。

在现实的集装箱运输中，由于对各种类货物的运输需求，班轮公司经常会使用多种类型集装箱，从而使得空箱也会存在多种不同的类型。在以往的相关研究中，基本不考虑多类型集装箱的影响。为了适应装载不同种类的货物，出现了许多不同类型的集装箱，例如杂货集装箱、敞顶集装箱、冷藏集装箱、散货集装箱和罐式集装箱等。另外，各种类的集装箱的尺寸也有不同类型，例如20英尺箱(TEU)、40英尺箱(FEU)等。在本文，我们主要考虑集装箱的尺寸不同对班轮航线设计和空箱调运问题的影响。

假如不同尺寸的空箱是可以相互代用的话，即箱种代用，必然可以大大降低空箱调运量和空箱调运成本。另外，需要指出的是，通用集装箱(例如杂货集装箱)与特种箱或专用集装箱(例如罐式集装箱、冷藏集装箱)之间一般是不能代用的。然而，不同尺寸的通用集装箱(或专用集装箱)之间显然是可以代用的。对于任何一个港口，不同尺寸的集装箱的装卸费用和装卸时间一般都是不同的。当一个港口存在不同尺寸的空箱可供调运时，选择什么尺寸的空箱调运到什么港口，是一个亟待解决的问题。本论文从减少总费用的角度，来探讨和确定各个港口是大箱代替小箱，还是小箱代替大箱，从而可有效减少班轮公司的运输成本。

本文在综合研究班轮航线设计和空箱调运的基础上，探讨各港口内部以及港口之间，不同箱种之间的最优代用。从定量的角度，分析了箱种代用对班轮航线设计和空箱调运问题的影响。

1 问题描述和参数说明

1.1 航线与船型

令港口集合为P。班轮公司分配船舶访问一些港口，形成一条班轮航线。令所有可行的航线集合为R。一般地，我们可以用船舶访问港口的顺序来描述一条航线r∈R，表示如下:

其中，pri表示航线r∈R上访问的第i个港口，Nr表示航线r∈R上的港口数量。很明显，一条航线形成一个闭合的环。为了更好地标记航线上访问的港口，引入函数

其中 mod 表示求余，即当 i=1，2，…，N 时，I(i，Nr)=i;当 i=Nr+1 时，I(Nr+1，Nr)=1。另外，根据实际运营的航线，一个港口也有可能被一个航线访问很多次。为方便标识访问的港口，引入Irp表示航线r∈R上的港口p∈P被访问的位置集合，则有Irp={i|pri=p，i=1，…，Nr}。

一般地，一个班轮公司都拥有不同类型的船舶，令其船舶类型的集合为V。不同的船舶类型，其船速、最大装载能力和运营费用均不同。对于一条航线r∈R来说，由于受到港口吃水能力等的限制，并不是所有种类的船舶可以被随意配置的。我们假设在航线r∈R上可配置的船舶类型集合为Vr。根据现实生活中班轮运输运营现状，不失一般性，本文假设对于任意一条航线上船舶的发船频率是按周服务的(weekly service frequency)。

1.2 费用和时间参数描述

令集装箱类型的集合为A。对于任意一条航线r∈R，假设配船v∈Vr。为简化模型，在不考虑进港托运时间、出港领航时间等相关时间的前提下，那么船舶在这个航线上运营的时间主要包括两个部分:(1)海上航行时间，记为τsearv(小时)，这个与航线的总距离和船型v∈Vr的航速相关;(2)航线上所有港口的集装箱装卸时间，这个与港口的装卸效率和集装箱数量相关，令tp，avr(小时)为在航线r∈R上的港口P处理一个船舶v∈Vr所装载的a∈A型集装箱所花费的时间。

对于任意一条航线r∈R，假设配船v∈Vr。那么对这个航线上运营的周费用主要可以分为三类:(1)船舶v∈Vr的周固定运营费用，记为cfixv(US$/week)，主要包括船舶造价的贷款、船舶的保险、船舶的维护维修的船员工资等;(2)船舶v∈Vr的油耗，令船舶v∈Vr在航行过程中每小时的油费为cbunkerv(US$/小时);(3)港口的集装箱装卸费用，港口的集装箱装卸费用与港口装卸的集装箱数量和单个集装箱的装卸费用相关。令cap(US$)为在港口P处理一个a∈A型集装箱的费用。

1.3 集装箱运输与箱种代运

对于任意给定的集装箱运输需求，令naod为从港口o∈P到港口d∈P每周需要运输的a∈A型集装箱数量，即O-D(origin-destination)对(o，d)之间的集装箱需求量。基于航线集合，集装箱完成从起点到终点的运输，形成一个集装箱的路径。集装箱的路径可能由若干条航线组成，不同航线之间通过共同的枢纽港进行中转。

为了描述集装箱的路径，借鉴文献［13］中有关一条航线上的航段(Segment)的概念。令S={＜k，l＞}为既服务于港口k，又服务于港口l的所有航线上的航段集合，且令Sr为航线r∈R上的所有航段集合。基于所有可行的班轮航线集合R，令Hod(R)为O-D对(o，d)之间所有可行的路径集合。Hklod(R)则表示O-D对(o，d)之间所有可行的路径，并包含航段 ＜k，l＞，且Hklod(R)∈Hod(R)。

为了描述港口p∈P的空箱情况，定义nec，ap为在港口p∈P所剩余的a∈A型空箱，且有

为了描述箱种代用问题，我们引入参数λa(a∈A)表示a∈A型空箱的代用能力。

2 混合整数规划模型

2.1 模型的假设条件

通过参考班轮运输的实际运营过程，本文作如下3个假设:

(1)重箱被中转不能超过2次;

(2)重箱只能在其枢纽港进行中转;

(3)任意两个枢纽港之间的集装箱运输只能是直航运输。

2.2 决策变量

在前面所述基础上，我们定义的决策变量有:

ξrv:为0或1变量，如果给航线r∈R分配船型v∈Vr时为1，否则为0。

mrv:为满足每周的服务频率，在航线r∈R上配置的v∈Vr型船的数量。

2.3 数学模型

针对本文研究的问题，本节建立如下的混合整数线性规划模型

其中，Rp表示服务于港口p∈P的所有航线集合。Rkl表示包含航段 ＜k，l＞的所有航线集合。δklri的取值是0或1，在航线r∈R上，若航段 ＜k，l＞∈Sr包含此航线上的两个相邻港口Pri和PrI(i+1，Nr)时为1，否则为0。Capv表示v∈Vr型船的最大装载能力。

公式(4)为目标函数，即极小化运营费用，由三部分组成，第一部分为运营上的固定费用和燃油费;第二部分为港口重箱处理费用;第三部分为港口空箱处理费用。公式(5)表示需求守恒约束。公式(6)表示航段流与路径流的关系。公式(7)表示空箱调运平衡约束，以及空箱之间的箱种代用关系。公式(8)说明空箱流守恒约束。公式(9)为船舶运输能力约束。本文假设为周服务频率，公式(10)是周服务频率的一个约束，其中168表示1周的小时数。公式(11)是对配船数量和是否配船的关系约束，其中M表示一个很大的数。公式(12)～(16)均为非负数变量约束。公式(17)为对非负整数变量的一个约束。公式(18)是对0或1变量的一个约束。

3 算例分析

在数值分析中，我们考虑亚洲－欧洲－大洋洲航线网络上一些典型的港口，如图1所示。对于船舶的类型，本文考虑3种不同的船型，与船型相关的一些参数如表1所示。针对集装箱的类型，本文侧重考虑2种:20英尺箱(TEU)和40英尺箱(FEU)。很明显，在空箱调运中，我们可以假设一个40英尺空箱可以代替两个20英尺空箱。在占用船舶空间(或容量)上，一个40英尺箱类似于两个20英尺箱。对于求解模型(4)～(18)所需的O-D集装箱需求量，是由一个国际班轮公司提供的。为了安全和保密起见，本文对这个O-D集装箱需求量进行了一定的修改，并且20英尺箱和40英尺箱的比例是随机给出的。为了给出合理的班轮航线集合，可以参考各大国际班轮公司(例如美国总统班轮、马士基班轮等)的网站。

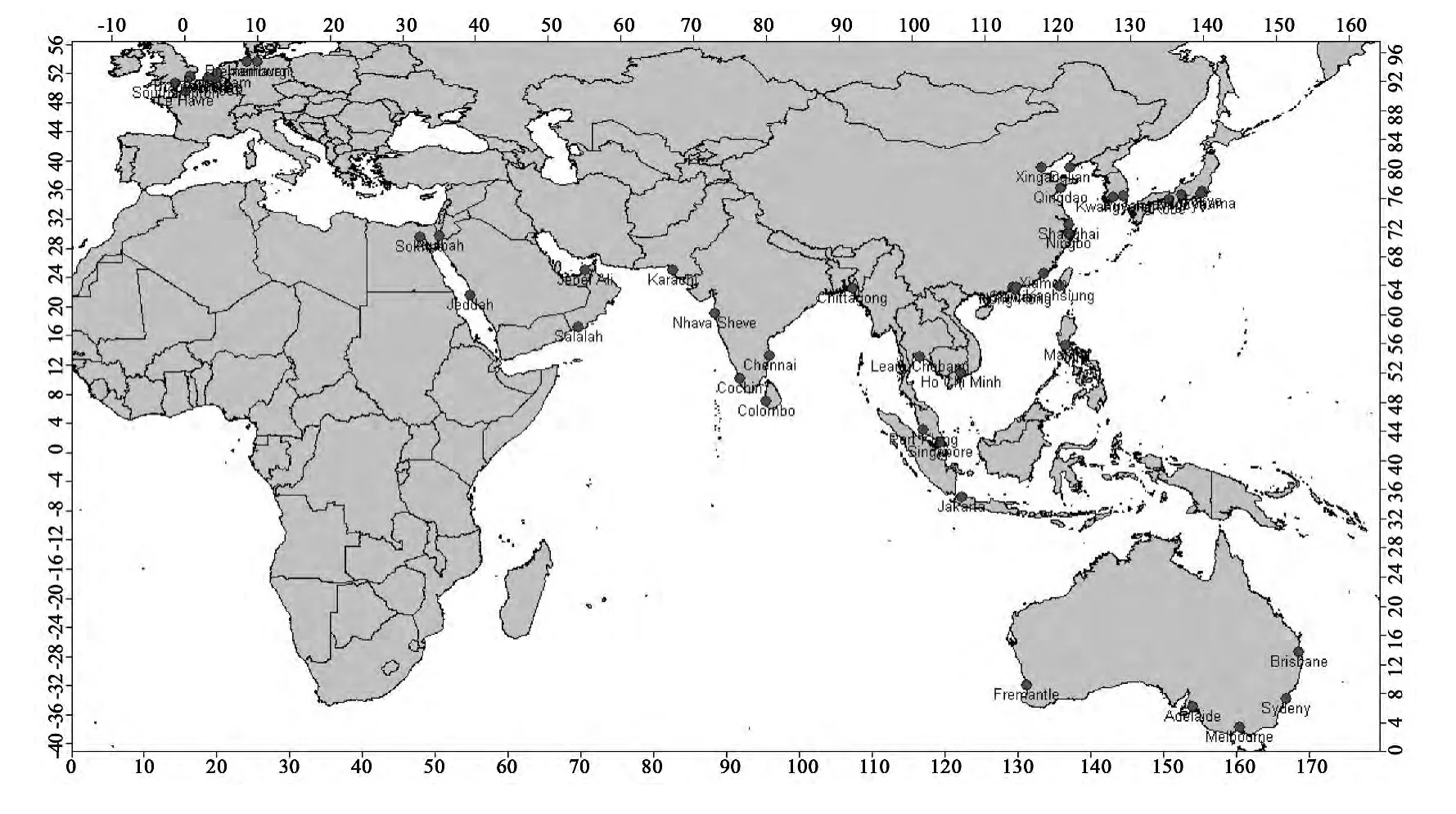
图1 亚洲－欧洲－大洋洲航线网络上一些典型的港口Fig.1 Some typical ports in Asia-Europe-Oceania shipping network

为了探讨引入箱种代用的影响效果，我们同样也考虑不同箱种不能代用的情况。很显然，如果不同箱种不能代用，那么我们应将约束条件(7)进行如下修改:

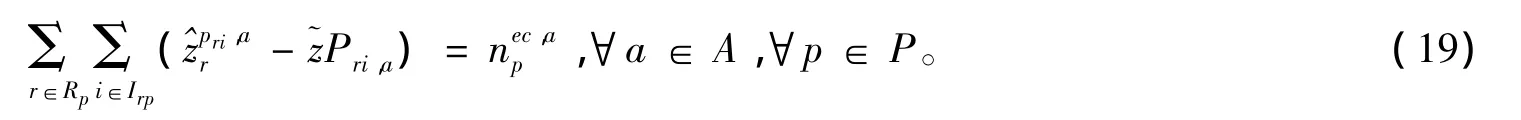
公式(19)表明，对于各种类型的空集装箱都得满足空箱调运平衡。

表1 各种船型及其相关参数Table 1 Various ship types and their related parameters

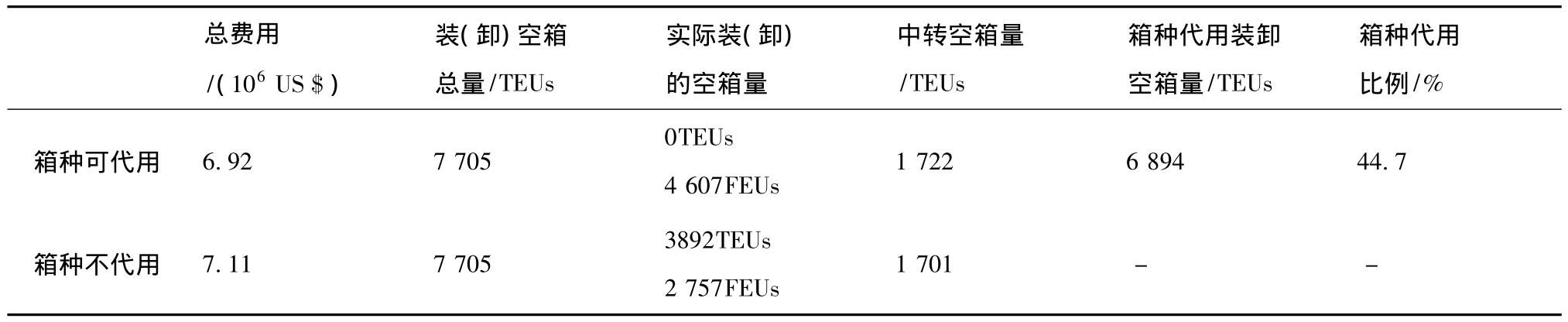
表2 两种情况的结果比较Table 2 Results comparison between two cases

从表2中可以看出，通过箱种代用的手段，每周在班轮运营和集装箱运输方面的总费用可以降低大约2.7%，即0.19×106美元。通过实际装或卸的空箱量可以看出，当箱种不代用时，20英尺空箱和40英尺空箱都需要完成调运和装卸，从而满足约束条件(19);当箱种可以代用时，实际完成装卸任务的只有40英尺空箱，那是因为1个40英尺空箱的装卸时间和费用一般要小于2个20英尺空箱的装卸时间和费用。对于一些港口，由于装卸机械的影响，当1个40英尺空箱的装卸时间和费用大于或等于2个20英尺空箱的装卸时间和费用时，很显然我们可以得到不一样的结果，在本文没有一一列出。另外，表2中也给出了发生中转的空箱数量，可以发现，两种情况下需要中转的空箱量相当。通过装(卸)空箱总量、实际装(卸)的空箱量和中转空箱量的数据可以看出，当箱种不代用时，中转空箱量都是通过一次中转完成运输的。从箱种代用的比例44.7%可知，发生箱种代用的空箱数量是很大的。另外，当箱种可代用时，发生虚拟装卸的空箱量是201TEUs，这个数没有在表2中列出，但是这个数已经包含在箱种代用装卸空箱量里面。

4 结语

通过引入多种类型集装箱，本文研究了考虑箱种代用条件下的班轮航线网络设计和空箱调运问题。为了求解这个问题，我们提出了一个混合整数线性规划模型。该模型可以通过CPLEX等常用的数学规划软件进行有效的求解。最后，通过亚洲－欧洲－大洋洲航线网络上集装箱运输的情况，对我们提出的模型进行了验证，并分析了空箱中转和箱种代用的情况。研究表明，通过箱种代用的手段，可以有效降低班轮公司的运输成本。

下面两个方面需要我们未来进一步地研究:

(1)本文假设班轮航线的候选集合，如何有效地产生合理的班轮航线网络是一个很重要的研究课题;

(2)一般来说，集装箱需求是不确定的，具有一定的波动性。研究集装箱需求不确定性下的班轮航线网络优化、船型分配和空箱调运问题具有更加重要的意义。

［1］UNCTAD.Review of Maritime Transportation 2010［EB/OL］.［2013 －11 －03］.http://www.unctad.org/en/docs/rmt2010_en.pdf.

［2］CONLEY J H，FARNSWORTH R S，KOENIGSBERG E，et al.A linear programming approach to the total movement of a homogeneous product［J］.Transportation Science，1968，2:289 －302.

［3］LANE D E，HEAVER T D，Uyeno D.Planning and scheduling for efficiency in liner shipping［J］.Maritime Policy and Management，1987，14(2):109 －125.

［4］RANA K，VICKSON R G.Routing container ships using Lagrangean relaxation and decomposition［J］.Transportation Science，1991，25(3):201－214.

［5］JARAMILLO D I，PERAKIS A N.Fleet deployment optimization for liner shipping Part 2:Implementation and results［J］.Maritime Policy and Management，1991，18(4):235－262.

［6］XIE X L，WANG T F，CHEN D S.A dynamic model and algorithm for fleet planning［J］.Maritime Policy and Management，2000，27(1):53－63.

［7］FAGERHOLT K.Optimal fleet design in a ship routing problem［J］.International Transactions in Operational Research，1999，6(5):453－464.

［8］FAGERHOLT K.Designing optimal routes in a liner shipping problem［J］.Maritime Policy and Management，2004，31(4):259－268.

［9］SAMBRACOS E，PARAVANTIS J A，TARANTILIS C D，et al.Dispatching of small containers via coastal freight liners:The case of the Aegean Sea［J］.European Journal of Operational Research，2004，152:365 －381.

［10］KARLAFTIS M G，KEPAPTSOGLOU K，SAMBRACOS E.Containership routing with time deadlines and simultaneous deliveries and pick －ups［J］.Transportation Research Part E，2009，45(1):210 －221.

［11］IMAI A，NISHIMURA E，PAPADIMITRIOU S，et al.The economic viability of container mega-ships［J］.Transportation Research Part E，2006，42(1):21－41.

［12］IMAI A，SHINTANI K，PAPADIMITRIOU S.Multi-port vs Hub-and-Spoke port calls by containerships［J］.Transportation Research Part E，2009，45(5):740－757.

［13］CRAINIC T G，DEJAX P，DELORME L.Models for multimode multicommodity location problems with interdepot balancing requirements［J］.Annals of Operations Research，1989，18(1):279 － 302.

［14］CRAINIC T G，GENDREAU M，SORIANO P，et al.A Tabu search procedure for multicommodity location/allocation with balancing requirements［J］.Annals of Operations Research，1993，41(4):359 － 383.

［15］CRAINIC T G，GENDREAU M，Dejax P.Dynamic and stochastic models for the allocation of empty containers［J］.Operations Research，1993，41(13):102 －126.

［16］CHOONG S T，COLE M H，Kutanoglu E.Empty container management for intermodal transportation networks［J］.Transportation Research Part E，2002，38(6):423 －438.

［17］LAM S W，LEE L H，TANG L C.An approximate dynamic programming approach for the empty container allocation problem［J］.Transportation Research Part C，2007，15(4):265 －277.

［18］DONG J X，SONG D P.Container fleet sizing and empty repositioning in liner shipping systems［J］.Transportation Research Part E，2009，45:860 －877.

［19］SONG D P，DONG J X.Flow balancing － based empty container repositioning in typical shipping service routes［J］.Maritimes Economics and Logistics，2011，13(17):61 －77.

［20］MOON I，NGOC A-D D，Konings R.Foldable and standard containers in empty container repositioning［J］.Transportation Research Part E，2013，49(1):107 －124.

［21］SHINTANI K，IMAI A，NISHIMURA E，et al.The container shipping network design problem with empty container repositioning［J］.Transportation Research Part E，2007，43:39－59.

［22］MENG Q，WANG S.Liner shipping service network design with empty container repositioning［J］.Transportation Research Part E，2011，47(5):695－708.

［23］SONG D P，DONG J X.Long-haul liner service route design with ship deployment and empty container repositioning ［J］.Transportation Research Part B，2013，55:188－211.