复杂场景下基于特征点匹配的目标跟踪算法

仇大伟，刘静

(山东中医药大学理工学院，山东济南250355)

目标跟踪是计算机视觉领域中的一个重要问题，在视频会议、目标监控和人机交互中有着广泛应用。目标跟踪的主要目的是在动态变化的场景下连续、可靠地获取目标的准确位置［1］，多年来，研究者们对此进行了大量研究，提出了一些目标跟踪算法。概括起来，目标跟踪算法可以分为以下四种类型［2］:基于梯度的方法通过最小化代价函数定位后续帧中的目标;基于知识的方法使用形状、轮廓等先验知识跟踪目标;基于学习的方法借助模式识别算法首先学习目标模型，然后在后续帧中搜索目标;基于特征的方法使用提取的诸如亮度、颜色和边缘等特征跟踪目标。

主动轮廓模型［3］自1988年提出后，一直是图像分割领域的研究热点，但是轮廓的初始化、运算速度等问题使其很难应用于目标跟踪的研究中。基于学习的方法［2，4－6］主要使用神经网络、径向基函数网络和支持向量机等方法进行目标跟踪。该方法允许进行复杂的、非线性目标建模，且可以动态地进行模型更新。然而，基于学习的方法一般用于特定的目标跟踪，且需要离线学习大量样本，通用性较差。近年来，基于特征的目标跟踪方法引起了研究者的广泛关注。均值偏移跟踪［7］(mean shift tracking，MST)及其改进算法主要利用颜色直方图表示目标，自提出以来得到了广泛应用。然而，该类算法假定目标的直方图在跟踪过程中不会发生较大改变，实际上，由于光照强度、观测角度、目标远近以及遮挡等情况的变化，目标在运动过程中常常会发生较大改变。针对不断变化的目标外形，Nejhum等［8］提出一种使用直方图跟踪目标的算法，该算法利用目标窗口中的若干小的矩形框表示目标，小矩形框的位置在算法运行过程中自适应地确定，该算法能够跟踪在运动过程中外形有较大变化的目标。然而，该算法每次都需扫描整个图像以确定目标的大体位置，表示目标的小矩形框的调整和再定位、目标模型的更新等方面也需要做出进一步的改进。

研究人员将局部不变特征应用于目标跟踪，也取得了较好的效果。Tang等［9］使用基于SIFT(scale invariant feature transform，SIFT)的属性关系图(attributed relational graph，ARG)表示目标，在几个连续的帧中总是出现的特征被认为是稳定的特征，用于构建图;反之，较少出现的特征则从图中删除。然而，在实际的视觉目标跟踪过程中，由于外观、光照等的变化，这样稳定的特征比较少。Carrera等［10］根据SURF(speeded-up robust features)算法提出了一种鲁棒的目标跟踪算法，该算法使用Harris算子检测目标区域中的兴趣点，使用SURF描述算子对兴趣点进行表示，在目标跟踪过程中，使用UKF(unscented kalman filter)预测目标中心位置。实验表明，该算法在目标旋转、尺度变化等情况下，鲁棒性较好。然而，在目标姿态、外观发生改变的情况下，该算法未能及时更新目标模型。

为减少计算量，有效应对目标跟踪过程中的遮挡、目标外观变化等情况，本文提出了一种基于SURF的目标跟踪算法。

1 SURF算法

SURF算法是Bay等［11－12］在2006年提出的一种具有尺度、旋转不变性的图像局部特征检测和描述算子。该算法不但在性能上达到或超过了目前常用的基于Harris、基于Hessian矩阵的方法和SIFT等算法，而且其执行速度更快。

1.1 兴趣点的检测

SURF算法的兴趣点检测算子基于Hessian矩阵，这样可以利用积分图像，极大地减少时间。

对于图像中的一个像素点X=(x，y)，在尺度σ下该点处的Hessian矩阵定义为

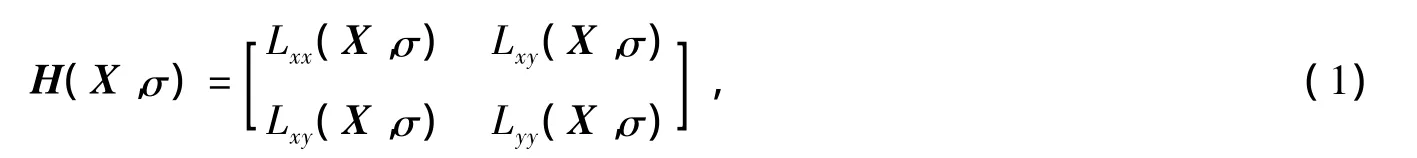
文献［13－14］中已经表明高斯核在尺度空间分析中性能优良，实际应用时须将其离散化。在SURF算法中，将二阶高斯微分算子近似为如图1所示的盒形滤波。使用这些算子SURF算法不但以较低的开销在积分图像上进行计算，且计算时间独立于滤波大小。

图1中的高斯二阶微分算子可记为Dxx、Dyy和Dyy。Hessian矩阵的行列式为

Lxx、Lyy和Lxy分别为Dxx、Dyy和Dxy与输入图像在某像素点处卷积，权值w按如下方式计算

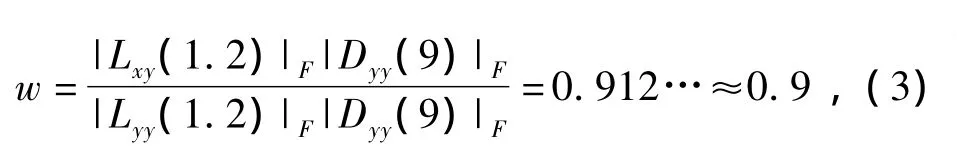
式中，|·|F为F-范数。

兴趣点从不同尺度检测，尺度空间通常表示为一个图像金字塔。由于积分图像的使用，SURF算法可以通过不断增大滤波而不是减小图像进行尺度空间分析，如图2所示，左图表示不断减少图像大小进行尺度空间分析，SURF算法使用右图所示方法，使用相同大小的输入图像，通过不断增大滤波大小进行尺度空间分析。

图1 高斯二阶微分算子Fig.1 Gaussian second-order partial derivative operator in x-，y-and xy-directions

尺度空间分成不同分组，为了使滤波大小为奇数且保证中心像素的存在，相邻滤波必须增大至少2像素。对于每一新的尺度空间分组，滤波增大加倍(从6～12到24～48)。在SURF算法中，第1分组的滤波大小分别为9、15、21、27，第2分组至第4分组中的滤波大小分别为15、27、39、51;27、51、75、99;51、99、147、195。

SURF算法运用非最大化抑制和插值方法寻找兴趣点。

图2 尺度空间分析Fig.2 Scale space analysis

1.2 兴趣点的描述

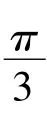
为提取兴趣点的描述，首先构造一个以兴趣点为中心，沿兴趣点方向的窗口，窗口大小为20s。该窗口被划分成4×4的小区域，在每个小区域计算Haar小波响应，水平方向记为 dx，垂直方向记为 dy(滤波大小为2s)。dx和dy与以兴趣点为中心高斯分布(σ=3.3s)进行加权。在每个小区域中计算向量v=(Σ dx，Σ dy，Σ |dx|，Σ |dy|)，连接4×4个小区域的向量，就可得到一个长度为64的向量。

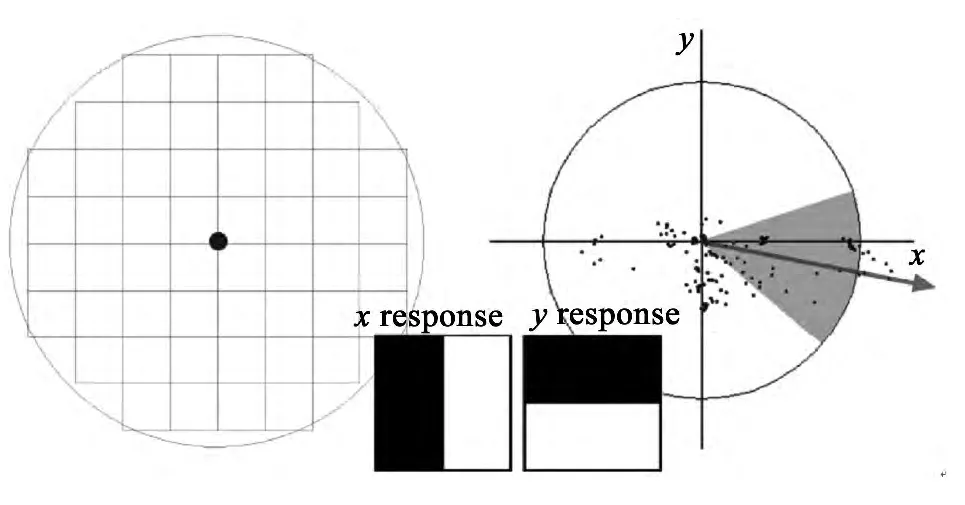
图3 兴趣点方向的指定Fig.3 Orientation assignment for the interest point

1.3 兴趣点的匹配

兴趣点的匹配基于向量间的距离，一般使用马氏(Mahalanobis)距离或欧氏(Euclidean)距离。

2 基于SURF的目标跟踪算法

在目标跟踪中，目标的表示、目标的检测、遮挡情况的处理、目标大小的缩放、目标模型的更新等是需要着重解决的几个问题，在本算法中，我们针对这几个问题提出了基于SURF的目标跟踪算法。

基于SURF的目标跟踪算法以第1帧图像中矩形框界定的目标为输入，后续帧中表示目标位置的矩形框作为输出。该算法的总体框架见图4。

算法获得输入后，对于每一帧新的图像，为减少计算量，不是在整个图像中搜索目标，而是首先根据目标的运动状态，计算目标搜索区域。算法在目标搜索区域中检测SURF点，将SURF点与目标模型中的SURF点进行比较，计算最佳匹配SURF点。然后，根据最佳匹配SURF点的个数，判定目标是否发生遮挡。若发生遮挡，则根据获得的匹配SURF点在目标模型中相对应的SURF点，计算目标中心，根据SURF点及其邻近R、G、B直方图计算目标的实际位置。若目标未发生遮挡，则根据检测到的最佳匹配SURF点，计算目标中心，根据SURF点邻近R、G、B直方图缩放跟踪窗口，计算目标的最佳大小和位置。并根据获得的目标窗口，重新计算窗口内SURF点及其邻近R、G、B直方图，对目标模型进行更新，以反映目标的最新变化。

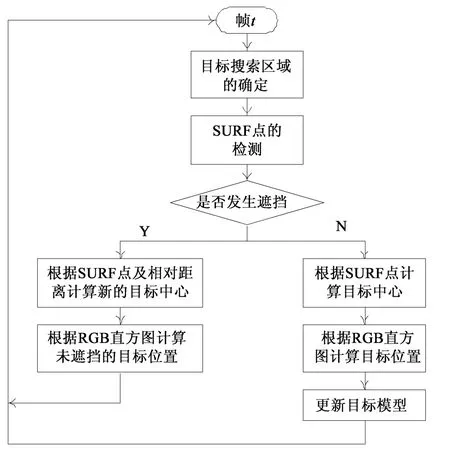
图4 算法框架图Fig.4 Flowchart of the tracking process

2.1 目标检测

目标检测是视觉跟踪的中心任务之一。本节的主要任务是计算目标的搜索区域，然后在该区域中检测目标的SURF点，这些点作为目标的主要特征点，确定了目标的大致位置，为后面计算目标的准确位置做必要的准备。

2.1.1 目标表示

本文提出的算法属于基于特征的目标跟踪算法。算法首先检测目标区域中的SURF点，然后计算每个SURF点邻近的R、G、B直方图，以SURF点和R、G、B直方图来表示目标。如图5所示，以目标跟踪窗口内的若干小矩形框的R、G、B直方图表示目标。在对跟踪的目标进行直方图的相似度比较时，不同的小矩形框赋以不同权值，离目标中心近的赋以较大权值，离目标中心较远的赋以较小权值，权值在算法运行过程中动态确定(权值的计算见2.3节)。在目标跟踪框中不可避免地会包含很多背景像素，对离目标中心较远的小矩形框直方图赋以较小权值，可以降低其对目标表示的影响，以便较准确地检测到目标，提高跟踪的精度。

图5 目标的表示Fig.5 Target representation

2.1.2 目标搜索区域的计算

为减少算法的计算成本，加快算法的执行速度，本算法不是扫描整个输入图像检测目标，而是根据上一帧图像中目标的位置和速度，在当前帧中扫描目标可能的邻近区域，进而确定目标的准确位置。目标可能邻近区域，即目标搜索区域的计算方法为:

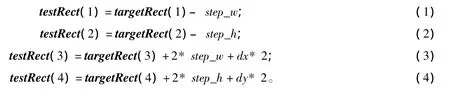
其中，testRect和targetRect分别表示当前帧的目标搜索区域和上一帧的目标区域。其第一、第二分量表示矩形区域左上角坐标，第三、第四分量分别表示矩形区域的宽度和高度。dx和dy分别表示目标在x和y方向上的速度，此处我们假定目标沿右下角方向移动，若目标向其他方向移动，目标搜索区域可相应向该方向增长。step_w和step_h分别表示矩形区域在宽度和高度方向上需要增加的量，其计算方法如下

其中，sw和sh分别表示目标搜索区域在宽度和高度方向上的增长系数，一般选择0.1～0.3，本文中sw和sh均设置为0.2。

目标搜索区域的计算见图6，图中虚线框为上一帧图像中检测到的目标的准确位置，点线框为原目标位置进行扩展后的区域。

图6 目标搜索区域的计算Fig.6 Computation of target searching area

2.1.3 SURF点的检测

确定了目标搜索区域后，应用SURF算法检测该区域中的SURF点，一般来说，在目标搜索区域中检测到的SURF点将多于目标模型中SURF点的数量。为计算最佳匹配SURF点，我们首先计算目标搜索区域与目标模型中SURF点的欧氏距离

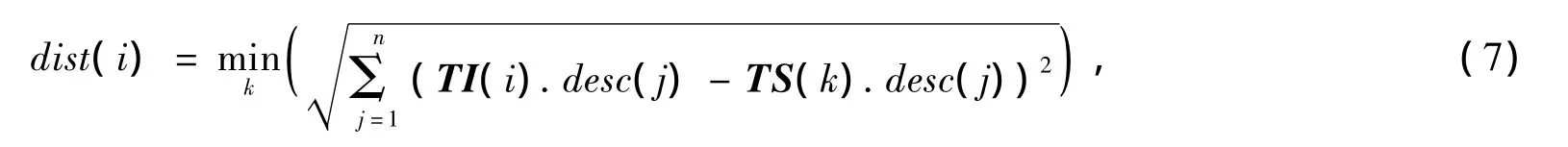
其中，TI(i)表示在目标搜索区域中检测到的第i个SURF点，TS(k)表示目标模型中的第k个SURF点。对于欧氏距离小于某一阈值θdist的SURF点，我们选定为最佳匹配点，其中θdist的值在算法运行过程中动态确定，一般为上一帧最佳SURF匹配点欧氏距离的最大值。

检测到的最佳SURF匹配点即为目标的大致位置，为计算目标的准确位置，需要计算目标的中心位置，为此算法将判断目标是否发生遮挡。

2.2 遮挡处理

为简单起见，算法根据如下原则，判断目标是否发生遮挡，并进行相应处理:

(1)若未检测到匹配点，则目标发生完全遮挡，在后续帧中，再次检测到与目标模型中相匹配的SURF点时，标志着目标再次出现。

(2)若匹配点的个数少于上一帧中最佳匹配点个数的75%，则目标发生部分遮挡。此时，目标中心根据目标模型中相应匹配点到中心的距离来计算，为方便说明，我们进行如下符号约定:目标模型中目标中心位置为O⇀

，目标模型中相应最佳SURF匹配点的位置为P⇀i，因此，目标中心到该点的距离为

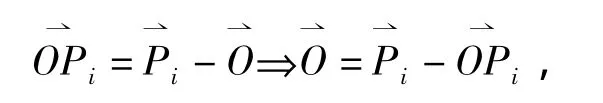
如图7所示。从而，当前帧目标中心的估计值为

其中，n为检测到的最佳匹配SURF点的个数。

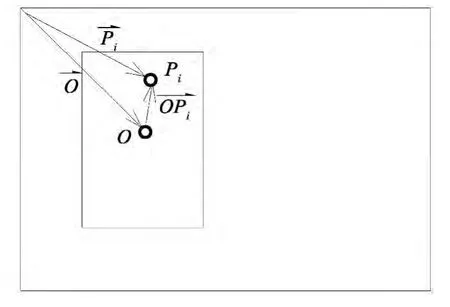
图7 目标发生遮挡时的目标中心位置计算Fig.7 Computation of the center position of a shaded target

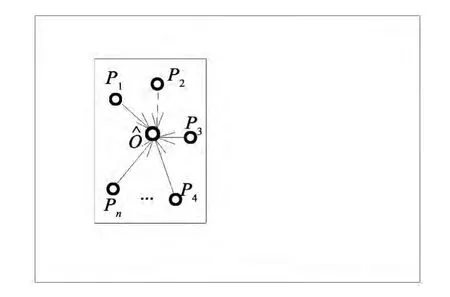
图8 目标未发生遮挡时的目标中心位置计算Fig.8 Computation of the center position without a shaded target

(3)否则，目标未发生遮挡，根据检测到的最佳SURF匹配点计算目标中心位置，见图8，目标中心的估计值为

2.3 目标缩放

检测到当前帧目标中心的估计值后，算法将根据最佳匹配SURF点邻近的颜色直方图来计算目标的准确位置。

根据上一帧中目标跟踪窗口的大小，在当前帧中，算法随机改变跟踪窗口的宽度和高度，对于每一个窗口W'=S(W，winw，winh)，其中W为上一帧中目标跟踪窗口，winw和winh分别为宽度和高度方向上窗口大小改变系数，本文中我们选取0.8≤winw，winh≤1.2。算法计算在该窗口内，最近匹配SURF点邻近的R、G、B直方图，并与目标模型中相应SURF点的R、G、B直方图进行比较，返回相似度最高的窗口大小，即

式中，n为最佳匹配SURF点的个数，θ(i)为相应于第i个匹配点的目标模型中的SURF点，λi为第i个SURF点邻近直方图的权重系数，在算法运行过程中动态改变，其计算方法为

其中，b为直方图箱子索引号，Hi为目标搜索区域中第i个SURF点邻近的原始直方图。ρ(·)度量目标区域和目标模板的R、G、B直方图的接近程度，本文对R、G、B三个分量采用相同权重，即均为1/3，算法采用Bhattacharyya距离

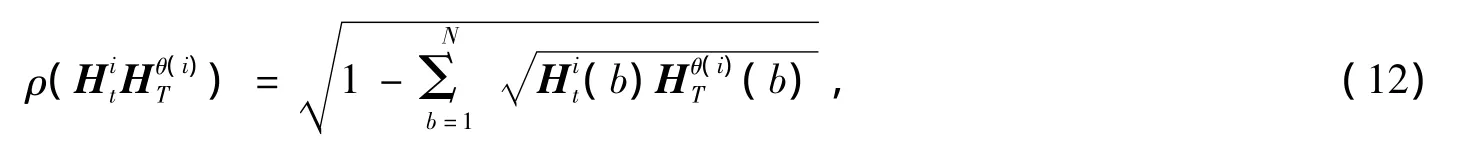
上式中，N为直方图箱数。

因为在本文中，目标跟踪窗口和直方图的计算均是矩形框，所以可以采用积分直方图以加快算法的执行速度。

2.4 模型更新

由于姿态改变、光线变化以及场景改变等因素的影响，目标在运动过程中其特征不断发生变化，目标模型应及时反映这些变化。因此，模型更新也是影响目标跟踪效果的一个重要方面。为此，本文提出了一种在线更新目标模型的策略。

在遮挡发生前，系统保存有最近未发生遮挡的前M(本文中，我们设置M为10)帧图像中的目标特征(SURF点、邻近直方图)。若当前帧中目标未发生遮挡，则根据2.3中计算目标的准确跟踪窗口，重新计算跟踪窗口内的SURF点邻近的R、G、B直方图，将SURF点即R、G、B直方图保存到目标模型中，若目标模型中的帧数超过M，则删除最前帧中的目标特征。

若当前帧中目标发生遮挡，停止更新目标模型，根据匹配的最佳SURF点及目标模型，估计可能的目标中心位置，计算SURF点邻近R、G、B直方图，输出目标未遮挡部分。

3 实验结果与分析

为了评价所提出算法的性能，通过几个实验对其进行测试，主要针对目标缩放、遮挡情况的处理。经典均值偏移(MST)算法［7］应用较为广泛，因此本文选择该算法作为对比算法。本文将选用PETS［15－16］作为测试数据集，该数据集在目标跟踪领域作为测试数据集得到了广泛应用。

3.1 目标缩放的对比实验

本次实验使用PETS2001［15］中数据集，在该数据集的视频中，目标由远至近，跟踪目标逐渐变大，图像大小为768×576。图9为使用不同算法的部分跟踪结果，其中左侧为经典MST算法的部分跟踪结果，右侧为本文提出算法的跟踪结果。实验中本文算法选用的参数为:最优匹配SURF点个数为12，目标模型中历史帧数为10，R、G、B直方图箱数为128。图9中从上到下依次为第329、333、343、360、379帧图像。

图9 目标发生缩放情况下的不同方法的跟踪结果比较Fig.9 Comparisons of tracking results of different algorithms for a zoomer target

从图9中可以看出，在目标大小发生变化的情况下，本文提出的算法可以较好地适应目标大小的变化，而经典MST算法在第360帧己不能很好地适应目标大小的变化，最终只能定位到目标的一部分。

3.2 遮挡情况的对比实验

在本节中，我们使用PETS2007［16］中的数据集，图像大小为720×576。图10为使用不同算法的部分跟踪结果，其中左侧为经典MST算法的部分跟踪结果，右侧为本文提出算法的跟踪结果。实验中本文算法选用的参数为:最优匹配SURF点个数为12，目标模型中历史帧数为10，R、G、B直方图箱数为128。图10中从上到下依次为第10、47、75、110帧图像。

从图10可以看出，从第47帧开始，经典MST算法的跟踪结果即开始偏离目标，在第75帧中，经典MST算法已经失去了目标。而本文提出的算法，即使在有遮挡的情况下，也可较好地跟踪目标，说明了本文算法的有效性。

图10 目标发生遮挡情况下的不同方法的跟踪结果比较Fig.10 Comparisons of tracking results of different algorithms for a shaded target

3.3 实验分析

本节从以下三个方面说明不同参数的选择对目标跟踪结果的影响。

3.3.1 SURF特征点个数的选择

SURF特征点并不是越多越好，如图11所示，从上到下依次为SURF特征点数4、8、12、16的跟踪结果。左侧分别表示不同参数下PETS2001［15］中第349帧的跟踪结果，右侧分别表示不同参数下第379帧的跟踪结果。

文献［8］中通过实验说明了使用单一直方图进行目标跟踪时，常常得不到令人满意的跟踪效果。从图11中也可以看出，SURF特征点选取得少，算法虽然也能较准确地跟踪到目标，但是并不能准确地定位到完整的目标大小。这是因为SURF特征点较少，这些特征点只能代表目标的局部特征，其R、G、B直方图表示目标的区分性不足。反之，SURF特征点选取得越多，跟踪结果受目标周边背景特征点的影响越大;再者，SURF特征点越多，每个特征点的邻近区域越小，其R、G、B直方图在最终目标跟踪结果中所占的权重也越小。所以，应选取适当数量的SURF特征点。实验表明，目标跟踪过程中，一般选取SURF特征点的数量为目标区域中检测到的SURF特征点数量的1/3，跟踪效果较好。

图11 不同SURF特征点个数下的跟踪结果比较Fig.11 Comparisons of tracking results corresponding to different numbers of SURF feature points

3.3.2 目标模型中历史帧数量的选择

直觉上，跟踪目标的特征在连续帧中相似度较大。因此，目标模型中历史帧数一般不会设置较大。

表1 目标在历史帧中的相似度比较Table 1 Object similarity comparison among the past frames

我们在选取的SURF特征点数分别为4、8、12、16的情况下，多次进行实验，在目标模型的最优SURF特征点匹配中，历史帧的使用情况如表1所示。从表1可以看出，当前帧中的SURF特征点主要与前3帧相匹配。所以，目标模型中历史帧数一般设置为3～5。

3.3.3 直方图中箱数量的选择

对于RGB图像来说，直方图的箱数最大为256。实验表明，箱数越大，越能较好地表示目标的特征。箱数的大小对算法的运行速度影响不显著。

4 结论

本文根据SURF相比于SIFT等特征提取方法在性能、执行速度等方面的优点，提出了一种基于SURF的目标跟踪和在线目标模型更新算法，该方法的时间复杂度较低，执行速度快，并能够在线实时更新目标模型。对于目标运动过程中突然改变运动方向，以及光照突然变化的场景下的目标跟踪算法是今后研究的方向。

［1］HU W M，TAN T N，WANG L，et al.A survey on visual surveillance of object motion and behaviors［J］.IEEE Transactions on Systems，Man and Cybernetics，Part C，2004，34(3):334 －352.

［2］BABU R V，SURESH S，MAKUR A.Online adaptive radial basis function networks for robust object tracking［J］.Computer Vision and Image Understanding，2010，114(3):297－310.

［3］KASS M，WITKIN A，TERZOPOULOS D.Snakes:Active contour models［J］.International Journal of Computer Vision，1988，1(4):321－331.

［4］MUSAVI M，AHMED W，CHAN K H，et al.On the training of radial basis function classifiers［J］.Neural Networks，1992，5(4):595－603.

［5］AVIDAN S.Support vector tracking［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2004，26(8):1064－1072.

［6］AVIDAN S.Ensemble tracking［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2007，29(2):261 －271.

［7］COMANICIU D，RAMESH V，Meer P.Kernel-based object tracking［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2003，25(5):564－577.

［8］NEJHUM S M，HO J，YANG M H.Online visual tracking with histograms and articulating blocks［J］.Computer Vision and Image Understanding，2010，114(8):901－914.

［9］TANG F，TAO H.Object tracking with dynamic feature graph［C］//2nd Joint IEEE International Workshop on Visual Surveillance and Performance Evaluation of Tracking and Surveillance，2005.Piscataway:IEEE，2005:25－32.

［10］CARRERA G，SAVAGE J，MAYOL-CUEVAS W.Robust feature descriptors for efficient vision-based tracking［M］//Progress in Pattern Recognition，Image Analysis and Applications.Berlin:Springer，2007，4756:251 －260.

［11］BAY H，TUYTELAARS T，van GOOL L.Surf:Speeded up robust features［C］//Computer Vision – ECCV 2006.Berlin:Springer，2006:404 －417.

［12］BAY H，ESS A，TUYTELAARS T，et al.Speeded-up robust features(surf)［J］.Computer Vision and Image Understanding，2008:110(3):346－359.

［13］KOENDERINK J J.The structure of images［J］.Biological Cybernetics，1984，50(5):363 －370.

［14］LINDEBERG T.Scale-space for discrete signals［J］.IEEE Trans Pattern Anal Mach Intell，1990，12(3):234 －254.

［15］PETS.Sequence 2［EB/OL］.［2014－02－10］.ftp://ftp.cs.rdg.ac.uk/pub/PETS2001/.

［16］PETS.Sequence 3［EB/OL］.［2014－02－10］.ftp://ftp.cs.rdg.ac.uk/pub/PETS2007/.