经典相空间与希尔伯特空间对比浅析

王杰芳 李玉晓 贾 瑜 赵维娟 胡 行 杨德林 梁二军

（郑州大学物理工程学院，河南 郑州 450001）

最早接触到相（Phase）这个词，应该是在做简谐振动物体的运动方程中。相位(ωt+)φ描述了做简谐振动物体的运动状态，初相φ描述了做简谐振动物体的初始运动状态。同相和反相是说两个做简谐振动物体的步调相同或相反。顾名思义，相空间（Phase Space）是描述运动状态的空间。经典质点的运动状态由坐标和动量(r,p)共同决定；而微观粒子的运动状态由波函数描述，任何时刻微观粒子的位置和动量都不能同时精确测量，二者满足不确定原理。这就决定了描述经典质点运动状态的相空间（经典相空间）与描述微观粒子运动状态的相空间（希尔伯特空间）一定是截然不同的两个相空间。

我们知道，量子力学有3种等价表述形式，分别是：薛定谔的波动力学表述[1-3]、海森堡的矩阵力学表述[2,3]和费曼的路径积分形式[4]。此外，还有一种量子相空间理论，这个理论凭借其自身的优势，也被作为一种表述形式在统计物理、量子光学和非线性物理等科学领域有着广泛的应用[5,6]。这个所谓的量子相空间理论表述，指的是把量子力学算符以一定的规则（例如Weyl对应规则）对应到 q-p 相空间经典的坐标-动量函数，导出量子态的 Wigner 函数，建立相似于薛定谔波动方程的Wigner函数的时间演化方程，建立经典力学与量子力学之间的对应关系。这个量子力学的量子相空间理论适合具有一定的经典力学和量子力学理论基础的读者进一步学习和应用参考，对于初学量子物理的学生或读者来说有一定难度。本文着重基本概念和基本物理思想的理解，从经典相空间通过类比过渡到量子的希尔伯特空间，目的是能帮助我们更容易、更深刻地理解波函数所处的希尔伯特空间。

1 描述经典质点运动状态的空间——经典相空间

用笛卡儿直角坐标系能够完全描述某时刻经典质点的确切位置 r( x,y,z)，但不能完全描述某时刻经典质点的运动状态。某时刻经典质点的运动状态由该时刻质点的坐标和动量(r,p)共同描述。为了能够完全描述经典质点的力学运动状态，由质点的坐标变量和动量变量作为坐标轴而构成的空间，称为经典相空间。某时刻质点的运动状态一定是相空间中的一点，称为相点。当质点的运动状态随时间改变时，代表运动状态的相点在相空间移动，会描绘出一条曲线，称为相轨迹。比如，一个质点在做三维运动，要完全描述质点在任意时刻的运动状态，就选择(x,y,z,px,py,pz)6个变量为坐标轴，构成一个6维相空间。推广到由N个大量经典质点组成的系统，每个经典质点的自由度是3，那么，由3N个坐标和3N个动量可以完全描述这N个质点组成系统的运动状态。由3N个坐标和3N个动量为坐标轴构成了可以完全描述经典系统运动状态的相空间，这是一个描述由N个质点组成的经典系统的6N维抽象空间。

一个系统的相空间通常具有极大的维数，相空间中每一个点代表了包括系统所有细节的整个物理态（系统每个粒子的位置坐标和动量坐标）。作为一个巨大维数的空间，它上面的每个点代表我们考虑的系统全部可能的态。不管一个系统有多复杂，该系统随时间的整体演化在相空间中被描述成一个相点沿着哈密顿正则方程所确定的轨道运动[7]。

2 微观粒子运动状态的表示空间——希尔伯特空间（Hilbert Space）

在微观领域中，微观粒子的运动状态由波函数描述，故又叫态函数。描述微观粒子运动状态的量子相空间将是由所有在特定区域平方可积的态函数组成的复函数空间，是一个满足态叠加原理的线性函数空间。每一个态函数对应一个物理上可实现的客观存在的微观粒子的运动状态。所谓在特定区域平方可积的函数ψ(x)是指满足下列条件的函数[8,9]，

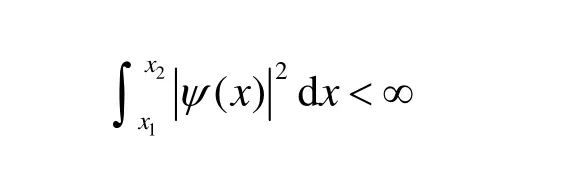
其中，积分上下限x1，x2在量子力学中通常是指势函数定义区间的左右边界坐标，这个区间可以是某个特定范围，比如(a,b)，也可以是整个空间（-∞+∞）。这个条件是波函数可以归一化所必需的。在这个线性函数空间中，定义两个波函数的内积为

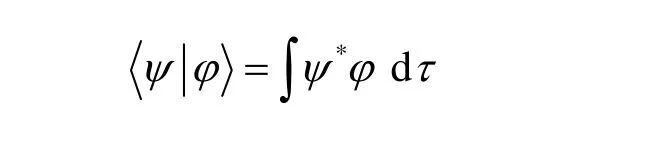
其中，∫dτ是对描述系统的全空间进行积分；dτ是空间体积元；,ψφ代表描述微观粒子运动状态的任意两个波函数。这个定义了内积的抽象线性函数空间，物理学家称为希尔伯特空间（Hilbert Space）[8]。在柯善哲编著的《量子力学》中也称为量子态空间[10]。

把每一个态函数ψ作为一个态矢量。当然，态矢量并非三维空间中的几何矢量，而是物理状态的抽象描述。全体态矢构成态矢空间，内积具有如下性质：

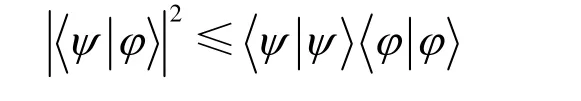
希尔伯特空间是一个完备的内积空间，平方可积函数的集合只是希尔伯特空间的一个例子，每一个有限维的矢量空间都是一个希尔伯特空间[8,11]。数学上的n维欧几里得（Euclidean）空间就是一个定义了内积的实数域上的有限维向量空间。希尔伯特空间是n维欧氏空间向无穷维的推广。每一个描述微观粒子运动状态的态函数在某确定时刻都是希尔伯特空间中的一点，当态函数随着时间演化时，将在希尔伯特空间描绘出一条曲线。

希尔伯特空间是量子力学的表示空间，很自然线性代数成为量子力学的描述语言。在线性代数中，存在于矢量空间的矢量可以通过平移、转动等操作从而变为该空间的另外一个矢量，每一个操作过程相当于对矢量进行的一个线性变换；同样，在量子力学中，存在于希尔伯特空间中的态矢量也可以通过平移、转动等操作而变为该空间的另外一个态矢量，每一个操作过程相当于对态矢量进行的一个线性变换，每一个线性变换对应一个量子力学中的力学量算符。

力学量算符的本征函数组可以有有限个、无数个，或者是连续的，那么以该力学量算符的本征函数组作为正交基矢的空间就是有限维、无穷维或连续维的。所以，希尔伯特空间可以是有限维、无穷维或连续维的。希尔伯特空间可以把任何一个力学量算符的本征函数组作为一组基矢，用来组合描述微观粒子的任何态矢量，因此态函数可以有坐标表象、动量表象或能量表象等。

在非相对论量子力学中，薛定谔(Schrodinger)方程是一个基本方程，在量子力学中其地位相当于牛顿动力学方程在经典力学中的地位。薛定谔方程的形式如下：

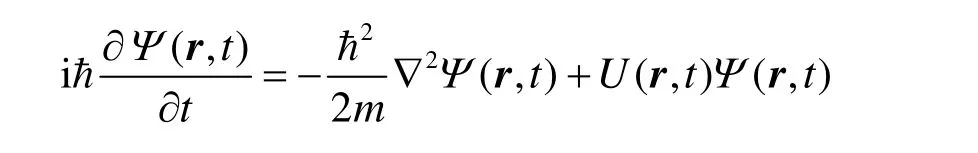
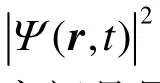
希尔伯特空间是量子力学的表示空间，波函数处于希尔伯特空间中，力学量算符相当于线性变换，作用于波函数之上，波函数随时间的演化遵从薛定谔方程。波函数和力学量算符是希尔伯特空间中的重要角色，它们是量子力学的两块理论基石。

3 结语

无论是经典相空间还是希尔伯特空间，共同点都是描述物体的运动状态。但是两者的不同点是显著的。本文通过对比的方式重点描述了经典相空间与希尔伯特空间的截然不同，有助于更深刻地理解描述微观世界的这套理论。它是一套完全不同于经典物理学的全新理论，必须用全新的物理思想和数学表述工具武装头脑，用全新的逻辑思维方式改变自己，才能深刻理解微观系统的行为。

[1] Feynman R P, Leighton R B, Sands M. The Feynman Lectures on Physics(Volume III)[M]. U.S.A.:Pearson Education, INC., 1989.潘笃武, 李洪芳, 译. 费恩曼物理学讲义(第3卷) [M]. 上海: 上海科学技术出版社, 2005.

[2] 周世勋. 量子力学教程[M]. 北京: 高等教育出版社, 2009.

[3] 曾谨言. 量子力学教程[M]. 北京: 科学出版社, 2008.

[4] 曾谨言. 量子力学(卷Ⅱ) [M]. 北京: 科学出版社, 2007.

[5] 吕翠红. 用IWOP技术和纠缠态表象发展量子相空间理论[D]. 合肥: 中国科学技术大学, 2011.

[6] 吕立强, 贾春霞, 隗功民, 等. 量子相空间中微扰理论[J]. 分子科学学报, 2006, 22(4): 231-237.

[7] 汪志诚. 热力学统计物理[M]. 4版. 北京: 高等教育出版社, 2008.

[8] David J. Griffiths著. 量子力学概论[M]. 贾瑜, 胡行, 李玉晓,译. 北京: 机械工业出版社, 2009.

[9] 柯善哲, 鞠国兴, 王均义, 等. 量子力学朝花夕拾(第二辑)[M]. 北京: 科学出版社, 2007: 48.

[10] 柯善哲, 肖福康, 江兴方. 量子力学[M]. 北京: 科学出版社, 2006: 84.

[11] 吴亚敏. 希尔伯特空间H中两种维数的比较[J]. 太原师范学院学报(自然科学版), 2013, 12(3): 36-37.