以弹跳机器人为背景的弹性环弹跳运动能量转换

王毅君 武烨存 刘 伟 史庆藩

（北京理工大学，北京 100081）

在当今信息时代，机器人正替代人类发挥着日益重要的作用.然而，随着应用范围的扩大，机器人面临的环境也越来越恶劣，例如有毒有害气体的腐蚀、日趋复杂的地貌等，这就要求机器人具有很强的自主运动能力及生存能力.特别是在遇到较大的障碍物时，机器人需要具有跳跃能力才可以轻易克服障碍，进而大大提高机器人的活动范围，于是弹跳机器人应运而生［1］.另外，在星际探索中，由于月球与火星表面重力加速度远低于地球，弹跳运动便是较为高效的运动方式，弹跳机器人也因此有着广泛的应用前景［2］.

目前，弹跳机器人已经有了一定的研究成果，但对于一些基本的弹性结构的弹跳还没有系统的理论分析及实验数据.另外，探究弹性环的弹跳高度也是2013年国际青年物理学家竞赛（IYPT）的题目之一.本文中我们选取最简单的弹跳模型即弹性环来探究弹跳机器人在跳跃时的高度以及能量转换的效率，以期对弹跳机器人的理论研究提供有价值的参考.

1 弹性环能量转换分析

弹性环在刚性表面（这里我们选择大理石）受力压缩后弹起，弹性势能转换为平动动能及振动动能.下面研究能量之间的转换并给出各部分能量的计算.

令弹性环的半径为R，厚度为τ，宽为w，初始形变量为δ，如图1和图2所示.

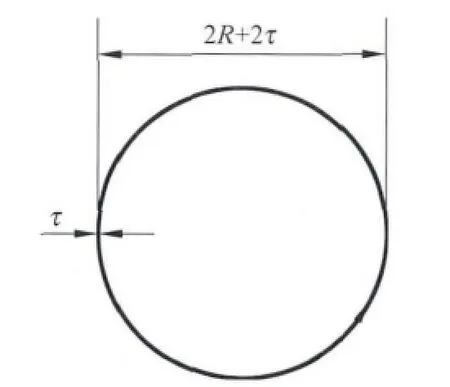
图1 初始状态的弹性环

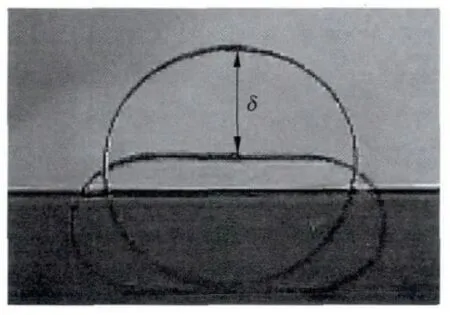
图2 压缩后的弹性环

弹性环处于压缩时，根据能量守恒定律可得

其中，Eb代表弹性环所储存的弹性势能；Es代表弹起过程中弹性环与接触面之间的能量损耗；Et，0和Ev，0分别代表脱离地面瞬间的初始平动动能及振动动能.

由文献［3］知，弹性势能计算为

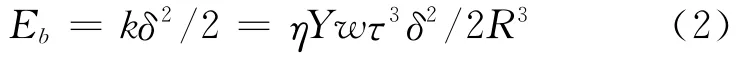
其中，k为弹性系数；Y为杨氏模量；η为一个无量纲常数.

初始平动动能为

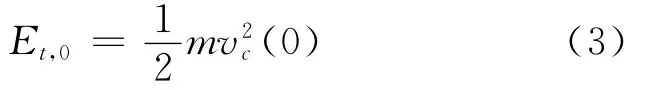
其中，m为弹性环的质量；vc是圆环质心的速度.初始振动动能为

弹性环弹起后，上升过程中克服空气阻力做功为Ed，则有

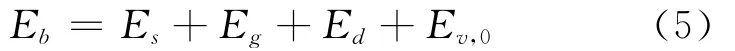
其中Eg代表上升达到高度为h的最高点时的重力势能，即

至此，我们推导出了能量之间的转换公式，下面就以此为基础计算忽略空气阻力时的弹起高度.

2 忽略空气阻力时的弹起高度

忽略空气阻力时，弹性环弹起的初始平动动能全部转换为达到最高点的重力势能.为了得到弹起高度，需要计算弹性势能以及初始平动动能.

弹性势能的计算首先需要对η进行实验测定.通过预实验我们发现在弹性限度内，外力F与δ的线性关系比较好，证明了胡克定律及弹性势能公式对弹性环的适用性.而后用多种规格的弹性环得到弹性系数k的结果如图3所示.

图3 多种规格弹性环弹性系数测量结果

线性拟合后斜率代表公式（2）中η，其值为0.1869.这样，对于给定参量的弹性环来说，初始的弹性势能便是已知量.

接着研究初始平动动能与弹性势能关系.将弹性环两端用细绳束缚压缩，而后将细绳与弹性环的接触部分点燃（见图4），以消除细绳摩擦的影响.弹性环跃起后，用高速摄像机采集数据后分析得到弹性环的初速度.

图4 点燃弹性环

实验中测量弹性环形变量δ后利用式（2）计算得到Eb；以圆环弹起瞬间最高点速度的一半为vc（0），利用公式（3）计算得到初始平动动能Et，0.Eb与Et，0二者之间关系如图5.

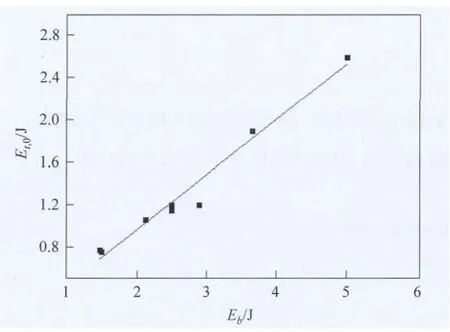
图5 初始动能与弹性势能的关系

Et，0≈0.4987Eb，进而计算得到振动动能Ev，0＝5／8Et，0＝0.3117Eb，起跳过程中的能量损失Es＝0.1896Eb，约为19%.

由初始动能与弹性势能的关系以及公式（3）也可以得到

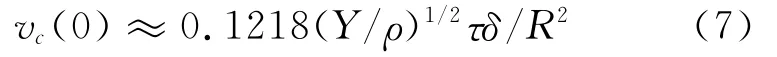
这样，有了初始平动动能占弹性势能的比例，就可以计算忽略空气阻力时的弹起高度.由于初始动能全部转化为重力势能，则有理论弹起高度h满足

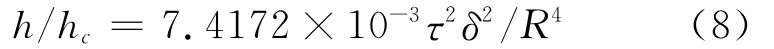
其中hc＝Y／ρg.

3 考虑空气阻力的弹起高度

由于初始动能与弹性势能的转换只存在于弹性环与底面接触时，并且这个阶段非常短暂，因此可以忽略该阶段空气阻力的影响.

在空气阻力表达式F＝CDρaRwv2c中，ρa代表空气密度，可以通过查表得知；CD代表空气阻力系数，需要通过实验测定.

我们采用测量弹性环处于竖直状态时的下落时间获得CD的值（水平下落时迎风面积太小，近似自由落体）.弹性环在下落过程中满足

对式（9）两端积分两次得

其中，hD＝2πρτρaCD；p＝－14／（m12·s－1），q＝

实验中求得一系列｛H（t），t｝，代入式（10）解出CD后，求均值得到CD≈2.088.

有了空气阻力系数，下面计算考虑空气阻力时的弹起高度.弹性环上升过程满足

对式（11）两端积分两次得

其最大值为

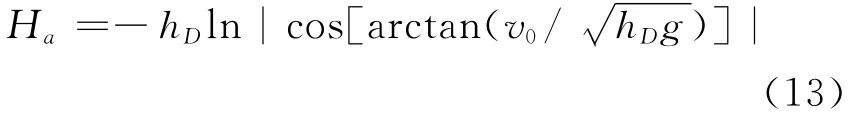
其中，v0＝vc（0）；hD＝2πρτ／ρaCD.

为作图方便起见，记式（13）为

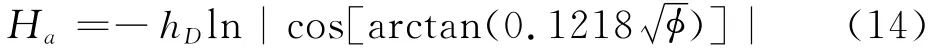
其中φ＝（hc／hD）（τ2δ2／R4）.

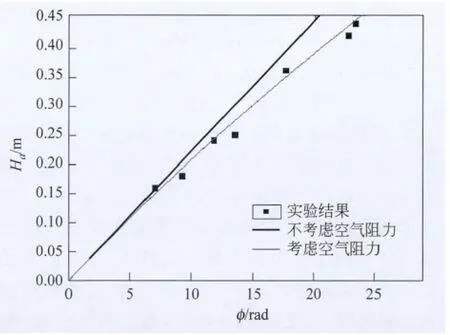
图6 理论值与实验观测值对照

理论计算结果与实验观测得到的弹起高度如图6所示.可以看出，忽略空气阻力仅在弹起高度较小时适用，而考虑空气后理论值与实际较为吻合.

4 结语

我们发现弹性环弹起时初始动能与弹性势能有着很好的线性关系，为计算不考虑空气阻力的理论高度打下了基础.而后通过实验发现在弹起高度较小时，空气阻力可近似忽略，而在高度逐渐增加后，忽略空气阻力的理论高度不再适用.于是考虑空气阻力后我们给出了考虑空气阻力后的理论高度，与实际结果吻合较好.本文对于弹性环这种简单弹跳模型的研究结果可以为弹跳机器人的能量转换效率及控制弹跳高度提供一个理论基础.另外，对于柔软的接触底面，能量的损失会大于18.96%，对应于实际中的比如土壤地面上的弹跳，这也有待于进一步探究.

［1］ 李保江，朱剑英.弹跳式机器人研究综述［J］.机械科学与技术，2005，（24）：803－807.

［2］ 杨小传，胡海拉，王培聪，等.弹跳机器人弹跳机理［C］／／福建省科协第五届学术年会数字化制造及其他先进制造技术专题学术年会论文集，2005.

［3］ Yang Eunjin，Kim Ho－Young.Jumping hoops［J］.American Association of Physics Teachers，2012（80）：19－23.