欧拉运动学方程的另一种推导方法

李文略

（湛江师范学院基础教育学院，广东 湛江 524037）

欧拉运动学方程的推导，关键是确定本体坐标系相对于空间坐标系的方位，也就是这两坐标系之间的转换关系.传统的推导方法是通过寻找并确定方向余弦矩阵来确定坐标系的转换关系，从而推导出欧拉运动学方程的［1－3］.笔者分别以“欧拉运动学方程”为篇名和关键词在知网搜索了国内近三十年的文献，除了文献［4］用向量回转法推导出欧拉运动学方程之外，没有发现有用其他方法推导该方程的了.文献［5］定义了方位矢量和转换张量，并用转换张量表示新旧坐标系的转换关系.受此启发，笔者将应用转换张量确定坐标系之间的转换关系，从而推导出欧拉运动学方程.

1 用转换张量表示新旧坐标系的转换关系

设坐标系χi为旧坐标系，坐标系χj为新坐标系，两坐标系的坐标原点相同.根据欧拉转动定理，新坐标系χj的方位可以由旧坐标系绕过原点的轴转动一个有限的角度λ而得到.设单位矢量u与转轴的方向相一致，可定义矢量λ（）u为坐标系χj的方位矢量.规定λ的正负与矢量u之间构成右手关系，λ与u为方位矢量λ（）u的两个参数.

文献［5］基于欧拉转动定理以及方位矢量的定义，定义了转换张量

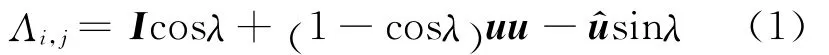
式中：I为二阶单位张量，u＾是用矢量u构造的升张量.并推导出了用转换张量Λi，j描述新旧坐标系之间的转换关系式，为

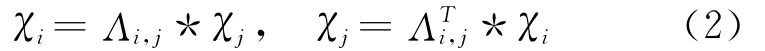
式中：ΛTi，j是转换张量Λi，j的转置张量.文中用＊号表示点乘.

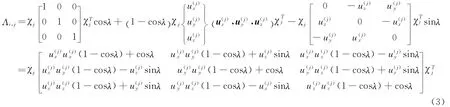
为了下文推导的简洁，将转换张量的定义式（1）用张量的解析形式写出上式中的矩阵为转换张量在坐标系χj中的伴随矩阵.矩阵中元素的上标“j”指明单位矢量u所在的坐标系，下标指明单位矢量u在所在坐标系下的分量.例如u（j）x表示的是单位矢量u在坐标系χj中x轴的分量.

2 欧拉运动学方程的推导

设作定点转动刚体的固定点为O点，以O点为坐标系原点建立两个坐标系：一个固定在空间的坐标系，称为空间坐标系χg（O－XYZ）；一个是固定在刚体上的坐标系，称为本体坐标系χb（O－xyz）.初始时空间坐标系χg与本体坐标系χb重合，刚体定点转动的方位可以用本体坐标系χb相对空间坐标系χg的取向来表明.根据欧拉转动定理，本体坐标系χb的方位可以通过空间坐标系χg按下面三个次序的连续转动来获得（图1）.转动的次序可用以下方式表示空间坐标系χg绕OZ轴旋转ψ角到达坐标系χ1（O－x1y1z1）的位置，再绕x1轴转动θ角至坐标系χ2（O－x2y2z2）的位置，最后绕z2轴转动φ角到达本体坐标系χb（O－xyz）的位置.三个角度坐标：ψ为进动角，θ为章动角，φ为自转角，统称为欧拉角.要唯一确定刚体的方位，欧拉角的取值范围为：0≤ψ＜2π，0≤θ≤π，0≤φ＜2π.

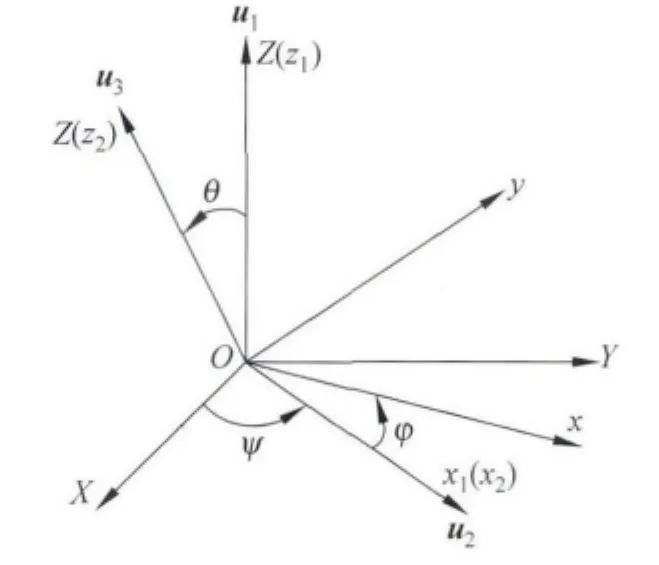
图1 空间坐标系的三次绕轴转动（y1，y2轴未画出）

根据方位矢量的定义，可知坐标系χ1相对于空间坐标系χg的方位矢量为（ψu1）.单位矢量u1在坐标系χ1中三个分量为：u（1）x＝0，u（1）y＝0，＝1.代入式（3）中，可得空间坐标系χ 与坐标g系χ1之间的转换张量为

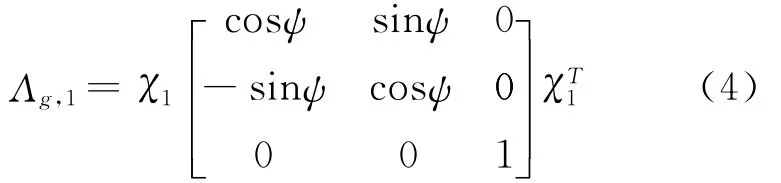
坐标系χ2相对于坐标系χ1的方位矢量为（θu2）.单位矢量u2在坐标系χ2中三个分量为：.代入式（3）中，可得坐标系χ1与坐标系χ2之间的转换张量为

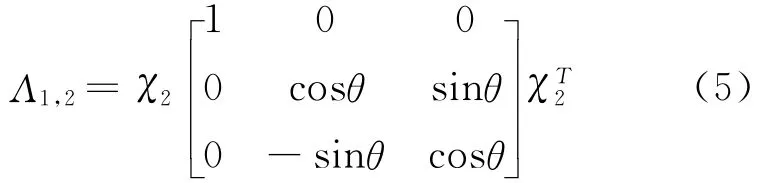
坐标系χb相对于坐标系χ2的方位矢量为（φu3）.单位矢量u3在坐标系χb中三个分量为：.代入式（3）中，可得坐标系χ2与本体坐标系χb之间的转换张量为

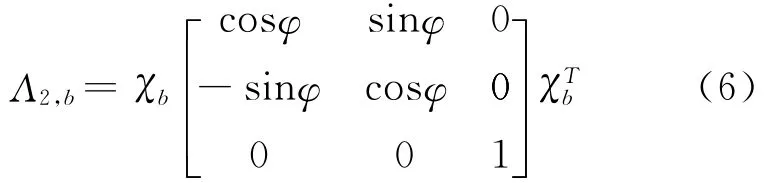
由式（2）中的第一个等式，可得空间坐标系χg与本体坐标系χb的转换关系为

由式（7），可知空间坐标系χg与本体坐标系χb之间的转换矩阵为

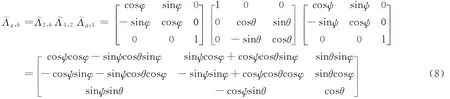
空间坐标系χg和本体坐标系χb用单位基矢量的矩阵形式写出

将式（8）、式（9）代入式（7）中，并进行一般的矩阵运算，可以得到空间坐标系与本体坐标系坐标系单位基矢量之间的转换关系为

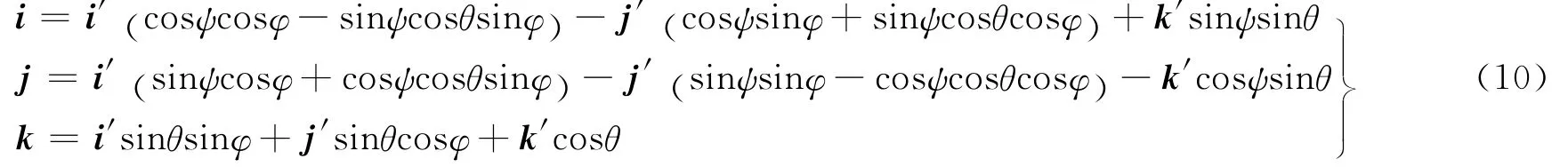
现在寻找单位矢量u2在本体坐标系χb中的解析表示.单位矢量u2在坐标系χ2和本体坐标系χb中的解析表达式满足下面的关系

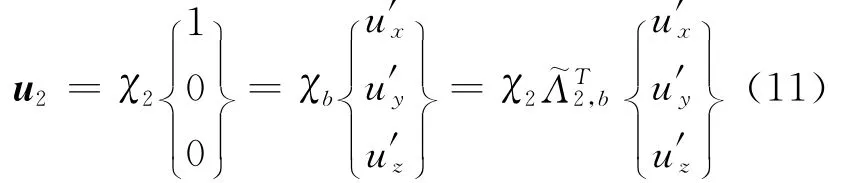
式中u′x、u′y、u′z分别表示单位矢量u2在本体坐标系χb中三个对应坐标轴上的分量是坐标系χ2与本体坐标系χb之间转换关系矩阵的转置矩阵.

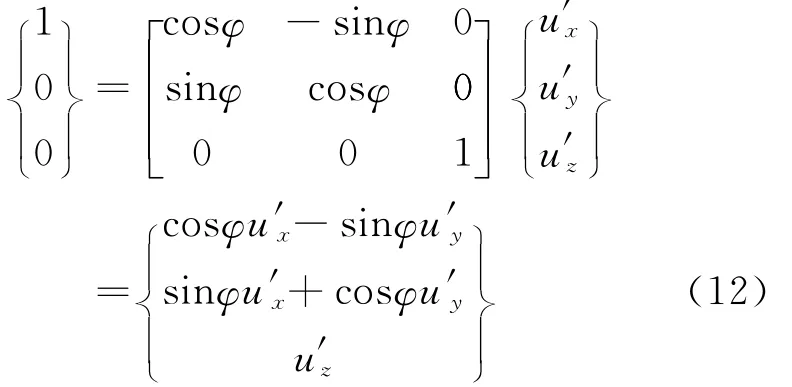
由式（12）可解出

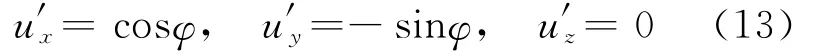
将式（13）代入式（11）中取第二个等号关系，可得到单位矢量u2在本体坐标系χb中的解析表达式为

刚体在空间中作定点转动的角速度ω可用欧拉角表示出来.刚体三次绕轴转动的角速度分别为、θ、.根据角速度的矢量合成法则，刚体做定点转动的角速度为

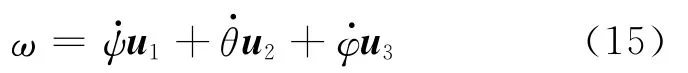
由图1可知：u1＝k，u3＝k′.将这两个关系、式（10）的第三个等式和式（14）代入式（15）中，整理得到角速度ω为

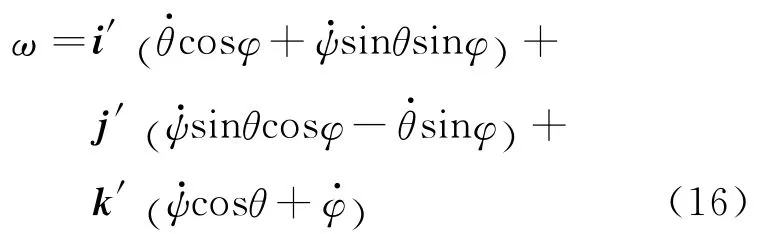
上式改写为角速度ω在本体坐标系χb中的分量式

角速度ω在空间坐标系χg和本体坐标系χb中用矢量的解析形式写出

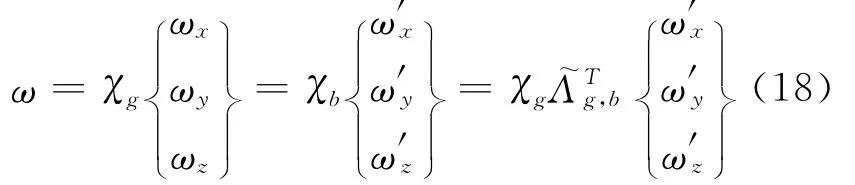
将式（8）、式（17）代入式（18）中，得到

对式（19）进行一般的矩阵运算，整理可得

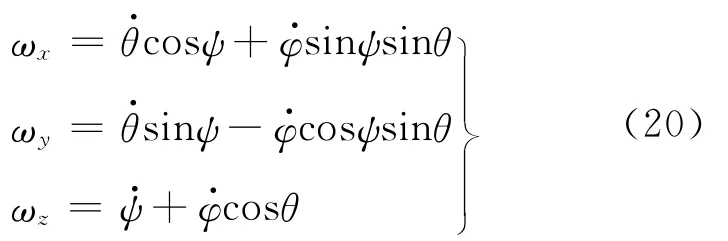
式（20）即为角速度ω在空间坐标系χg中分量式，即为在空间坐标系χg中的欧拉运动学方程.至此，刚体定点转动的欧拉运动学方程已推导完毕.

3 结语

确定方位矢量的两个参数，由式（3）即能确定空间坐标系和本体坐标系之间的转换张量，从而能确定这两坐标系的转换关系，这是推导欧拉运动学方程的关键.根据欧拉定理，刚体定点转动后的方位，可以通过刚体三次连续定轴转动来确定.依据方位矢量和转换张量的定义，通过确定三次定轴转动的转轴即能确定空间坐标系和本体坐标系之间的转换关系，从而推导出欧拉运动学方程，这要比用传统的方法形象直观.

［1］ 李俊峰，张雄.理论力学［M］.北京：清华大学出版社，2010：46－48.

［2］ 沈惠川，李书民.经典力学［M］.合肥：中国科学技术大学出版社，2006：38－41.

［3］ 吴大猷.古典动力学［M］.北京：科学出版社，1983：58－59.

［4］ 尧国庆，邱声书.推导欧拉运动学方程的向量回转法［J］.大学物理，1985（7）：12.

［5］ 李洲圣，唐长红.三位空间张量分析的矩阵方法［M］.北京：航空工业出版社，2010：32－34.