基于卡尔曼滤波和模糊集的地下水污染羽识别

江思珉，张亚力，周念清，赵 姗

（同济大学 土木工程学院，上海200092）

我国地下水污染状况已十分严重.与地表水体相比，地下水一旦遭受污染其治理和修复通常需要更长的时间（常持续30年以上），其治理和修复费用往往极为昂贵.在地下水污染治理和修复过程中往往需要有污染羽的时空描述资料.对污染羽进行时空描述通常需要通过建立相应的地下水污染监测网，以获取地下水的物理特性、化学特性和生物特性在时间、空间上的变化特征数据［1］.

在地下水水质的监测过程中，过量取样和取样不足是比较常见的问题.过度取样会造成不必要的取样和分析费用，而取样不足则不能获得污染物随时空变化的准确信息，进而不能确立地下水污染治理和修复的合理方案［2］.因此，文献［3－7］通过对地下水污染监测网进行优化设计，可以在不降低监测精度和不影响评价风险的前提下减少不必要的取样或增加必要的取样，从而以尽可能少的费用准确地识别出地下水污染羽.

地下水系统是一个受多种因素影响的复杂系统，存在着各种不确定性.诸多不确定性的存在使得很难准确地刻画地下水中污染物的空间分布特征，主要的不确定性因素包括场地信息的不确定性和污染源（位置和强度）的不确定性等［8－10］.在污染源位置未知和场地信息不确定性的前提下，本文基于卡尔曼滤波技术和模糊集合理论提出一类地下水污染羽识别的新方法，能够以尽可能少的采样点达到污染羽准确识别的目的.

1 污染羽识别算法

在进行地下水污染治理和修复过程中，通常需要以尽可能少的水质采样点达到准确识别地下水污染羽的目的.在场地信息不确定的前提下，可以选择使污染浓度场的不确定度减少最大的点作为采样点［11－12］.

1.1 基本假设

①污染源的强度已知；②地下水模型仅考虑渗透系数的不确定性.

1.2 算法流程

图1为污染羽识别算法的流程图.具体计算步骤如下：①确定污染源可能存在的位置，并对每个可能位置赋以概率值作为初始权重.权重值介于0～1之间，0表示该位置不存在污染源，1表示该位置存在污染源；②利用地质统计软件SGeMS生成场地的渗透系数随机场［13］；③构建地下水流模型与溶质运移模型，通过蒙特卡罗（Monte Carlo）随机模拟得到污染浓度场库；④根据污染源权重随机选取污染浓度场，提取滤波区的浓度场，经统计分析得到初始的综合污染羽和浓度误差协方差矩阵；⑤结合已有采样点资料，利用卡尔曼滤波技术对综合污染羽及误差协方差矩阵进行更新；⑥通过误差协方差矩阵寻找新采样点；⑦结合新采样点利用卡尔曼滤波技术更新综合污染羽；⑧利用模糊集合理论将综合污染羽与单个的污染源所对应的污染羽进行对比，得到污染羽的相似度；⑨根据相似度更新污染源权重.○10判断权重值和不确定度是否趋于稳定，满足则停止计算，否则回到步骤④.

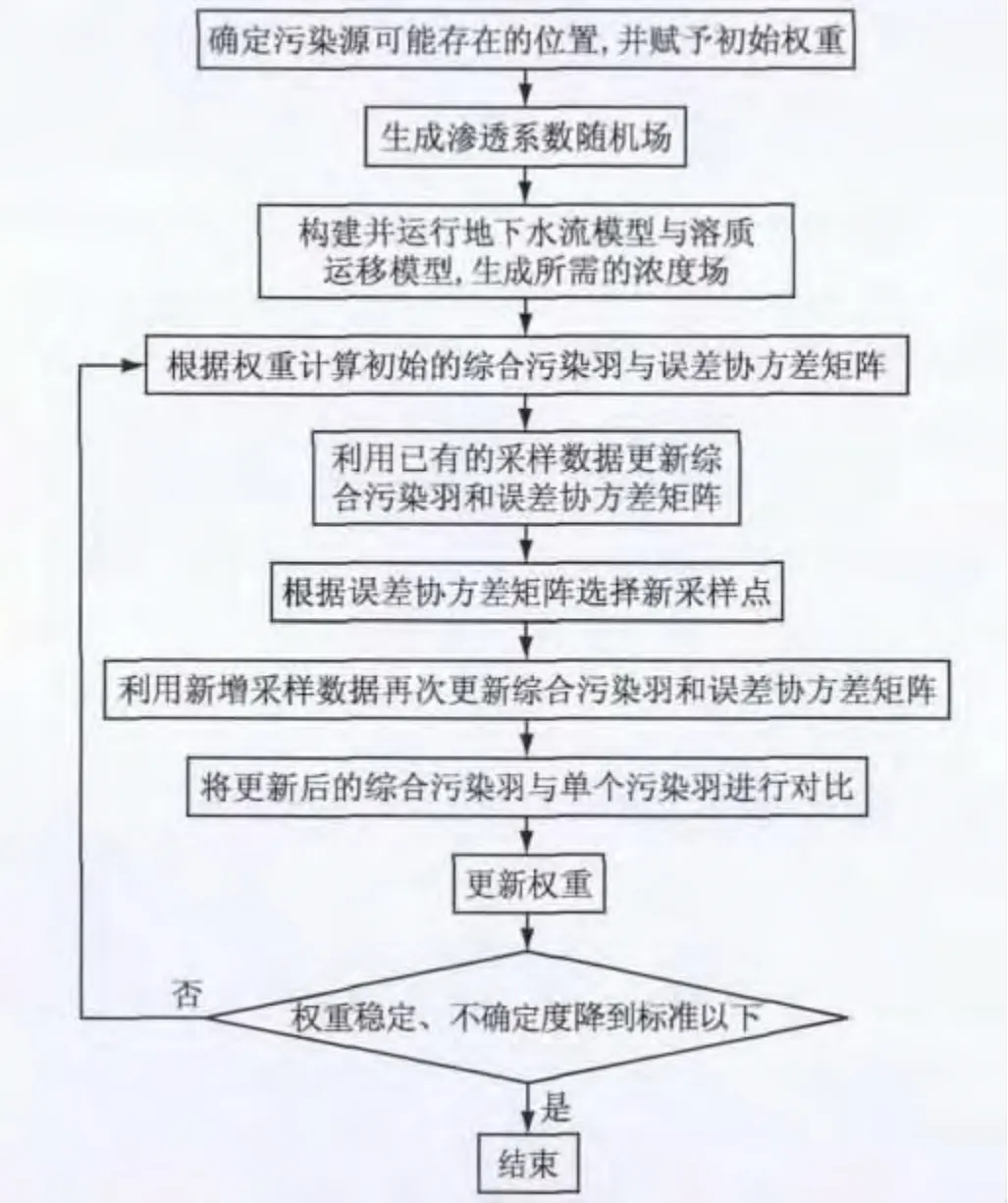
图1 污染羽识别算法流程Fig.1 Flow chart of the algorithm for identification of contaminant plume

1.3 综合污染羽生成与误差协方差估计

借鉴文献［14］的个体适应值库的概念，在利用蒙特卡罗随机模拟方法生成污染浓度场时将模拟结果存入污染浓度场库.如果污染源可能存在于m个位置，且渗透系数随机场有q次实现，则将可能的污染源与渗透系数场进行组合，可生成m×q个污染浓度场.

根据污染源权重大小，从各个污染源所对应的q个浓度场（对应于渗透系数场的q次实现）分别随机选取浓度场.在所有被选取出的污染浓度场中将相同渗透系数场所对应的浓度场叠加，得到当前污染源权重下的浓度随机场的q次实现，即统计意义上的q个样本.

对浓度随机场数据（q次实现）进行统计分析，可以估计出综合污染羽的浓度值以及浓度误差协方差矩阵.浓度随机场（q次实现）的均值即为综合污染羽的浓度，节点j处的浓度值记为.浓度误差协方差矩阵中的元素为R（ci，cj），其表达式为

式中：ci，k与cj，k分别表示在第k个污染浓度场中位置i和位置j处的浓度值分别表示在位置i和位置j处的平均浓度值（即综合污染羽的浓度值）.需要说明的是，上述对浓度随机场（q次实现）数据的统计分析（综合污染羽生成和误差协方差矩阵估计）并未在整个研究区（含水层）进行，而只在滤波区（即应用卡尔曼滤波技术的区域）进行.

2 污染羽的更新和新采样点的选取

2.1 综合污染羽的更新

卡尔曼滤波是由卡尔曼在1960年推导出的一种线性、无偏且误差方差最小的优化估计方法，它在已知系统模型和量测数学模型、量测噪声统计特征及系统状态的初始情况下利用量测数据获取系统状态变量的最优估计值［15］.

利用卡尔曼滤波技术通过连续作用采样点更新综合污染羽与误差协方差矩阵.卡尔曼滤波的更新方程如下.卡尔曼增益矩阵为

浓度更新方程为

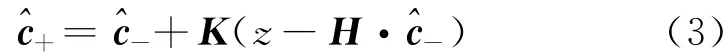
误差协方差更新方程为

式中：K为卡尔曼增益矩阵；P为n阶浓度误差协方差矩阵，下标－，＋分别表示先验估计和后验估计，对应利用测量数据更新之前和更新之后的状态；H为量测矩阵，通常为l×n阶的矩阵，l为取样点的数目，n为用于计算的网格点个数（滤波区内）；r为采样误差的方差；＾c是n维状态向量，表示浓度估计值；z为采样值；I为n阶单位矩阵.通过连续添加单个采样点对综合污染羽及误差协方差矩阵进行更新，此时H为一个1×n阶的矩阵，其形式如下：

其中，向量元素仅在采样点处取1，其他位置取0.若已知采样点的位置和采样值，可以利用式（2）～（5）更新综合污染羽.需要说明的是，初始的＾c－和P－的计算方法见1.3节.

2.2 新采样点的选取

随着采样点的增加，污染浓度场的不确定度（即误差协方差矩阵的对角线之和）会逐渐降低.新采样点的选取方法如下：首先将滤波区已有采样点之外的其他网格点视为备选采样点，分别利用卡尔曼滤波的更新方程（式（4）和式（5））得到更新后的误差协方差矩阵，然后计算各备选采样点对应的不确定度，最后选择不确定度最小的点作为新采样点.

本文采用一种更为简便的方法，就是寻找更新后的不确定度下降最大的点，将其作为新采样点.更新后的不确定度可以表示为更新前的不确定度减去新增采样点使不确定度下降的量［11］，即

3 污染羽的模糊对比

单个污染源的污染羽定义为该污染源在渗透系数随机场的所有实现下的浓度均值.如果有5个污染源，则可以生成5个单个污染源的污染羽.通过将单个污染源的污染羽与利用卡尔曼滤波更新后的综合污染羽进行对比，对污染源可能所在位置的权重进行更新，从而确定污染源位置.

首先将污染羽用模糊集来表示，隶属函数为标准化的浓度值c′（定义为浓度值除以最大浓度值）.在考虑数个模糊集时，每个模糊集中的值均小于一个给定的标准αs.若αs分别取值为0.2，0.4，0.6，0.8，则共可得到4个模糊集.

在某一αs下，将单一污染源的污染羽的模糊集分别与综合污染羽的模糊集进行对比，计算交叉面积为Ss，如图2所示的交叉面积表征单一污染源的污染羽与综合污染羽的相似度.全局相似度g为各个标准αs下的相似度的加权和［12］，即

图2为2个模糊集的比较，它一方面考虑了污染羽截面的形状，另一方面也考虑对污染羽中浓度较高的区域赋以较大的权重.污染源新的权重通过污染源全局相似度进行标准化后得到，具体就是将各相似度除以它们中的最大值，得到的就是标准化的相似度.

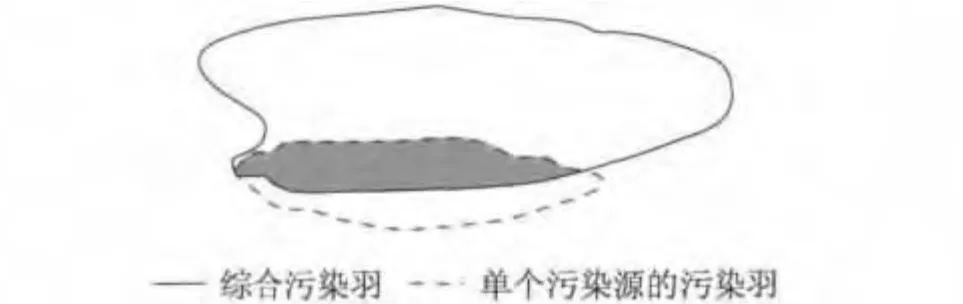
图2 综合污染羽与单个污染源污染的模糊比较Fig.2 Comparison of composite plume and individual source plume

4 算例

4.1 问题概述

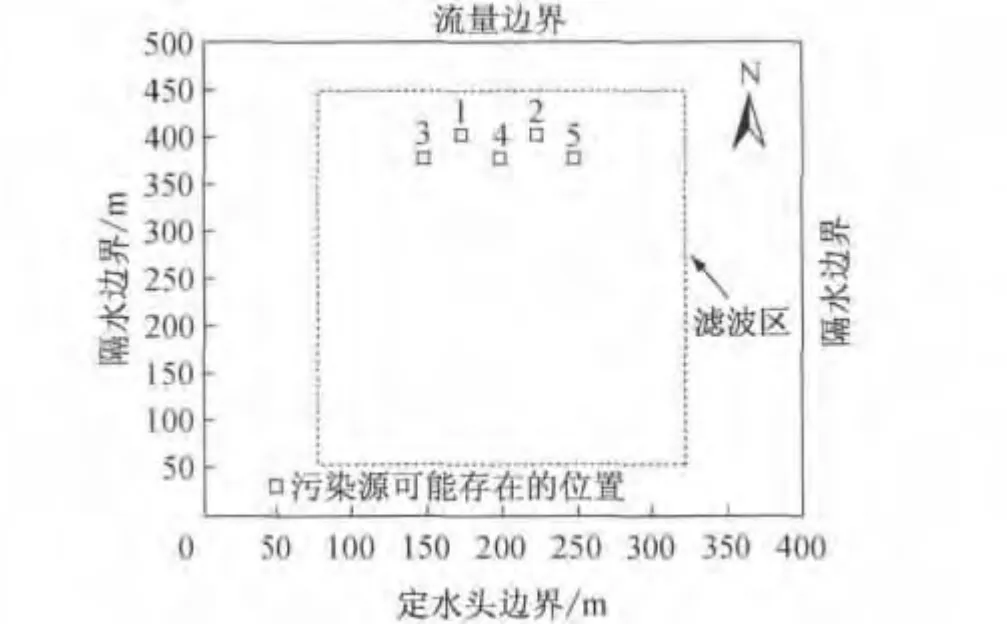
图3 含水层结构平面Fig.3 Plan view of confined aquifer

如图3所示，研究区存在二维非均质各向同性的承压含水层，尺寸为400m×500m，用边长为5m的正方形网格将研究区域剖分为100行、80列的有限差分网格.假设含水层水流运动为稳定流，含水层厚度为10m.上边界为二类边界，单宽流量为1.0 m2·d－1，下边界为定水头边界，水头为0 m，左、右边界为隔水边界.含水介质孔隙度为0.3，纵向弥散度为40.0m，水平横向弥散度为1.2m.已知污染源体积注入率和污染物浓度，分别为1m3·d－1和500 mg·L－1，但污染源位置未知.

含水层的渗透系数为一随机变量，且服从对数正态分布，其均值和标准差σlnK分别为2.62和0.53，在x方向和y方向的相关长度均为140m，变差函数为指数型.图4为渗透系数lnK场的一次实现.根据已有的场地信息，污染源可能存在的位置如图5所示，其中位置2为污染源的真实位置（事先未知）.本算例是在含水层参数不确定、污染源位置未知条件下通过择优选择采样点识别地下水污染羽.

图4 渗透系数随机场的任意一次实现Fig.4 One randomly selected stochastic hydraulic conductivity field

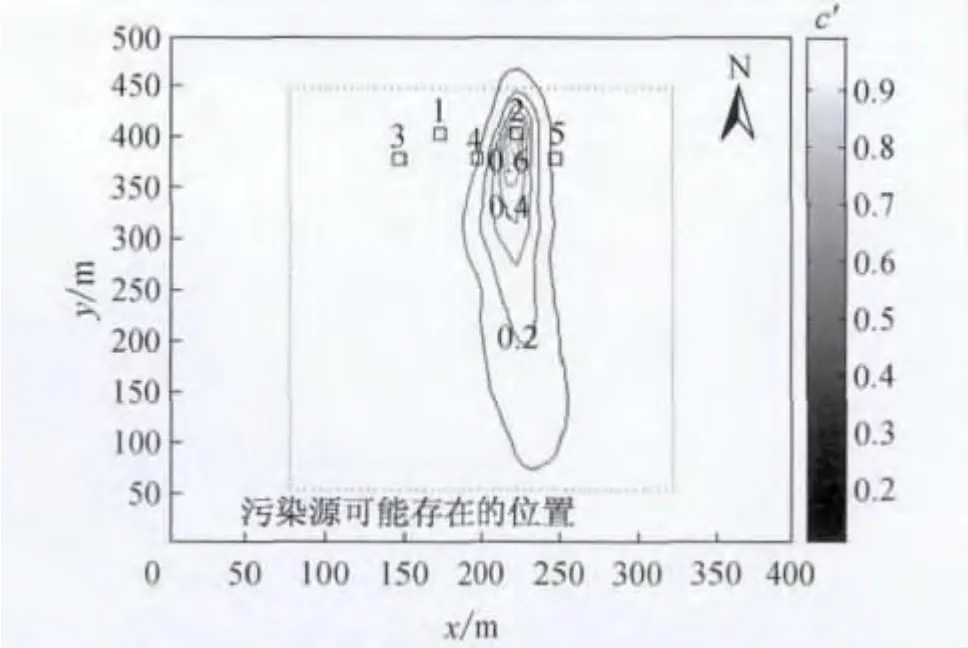
图5 真实的污染源位置和对应的污染羽分布Fig.5 True source location and the corresponding plume distribution

本算例中，渗透系数随机场共有100次实现，污染源可能存在的位置为5处，将渗透系数随机场的每次实现分别与各个可能的污染源结合，进行蒙特卡罗随机模拟共得到500个污染浓度场.为了减少调用模拟计算的次数，将这500个污染浓度场存入污染浓度场库.之后的计算中，只需要根据每次更新后的污染源权重随机选取浓度场即可.卡尔曼滤波区为图3虚线包围的网格.

污染羽识别算法的主要参数设置如下：污染源初始权重分别设为0.80，0.85，0.90，0.95，1.00.污染羽的模糊对比采用3 个模糊集，对应的标准为0.2，0.4和0.6.

4.2 算例分析

图6a为根据污染源初始权重计算得到的综合污染羽，图6c—6h为利用1个、6个和7个采样点更新后的污染羽及其对应的污染源权重.

由图6c—6h可知，经过7 次采样后，位置2 权重稳定于1，其他位置权重接近于零，同时将图6g与真实的污染羽形态进行比较，两者形态十分接近，表明只需要7个采样数据就可以确定污染源的位置，并能够达到较为准确地识别污染羽的目的.此外，由图6g可以看出，4个采样点（点2，4，5，6）分布在临近污染源的下游方向，其余3个采样点（点1，3，6）起到控制污染羽形态的作用.上述结果表明，采样点的分布主要考虑2个因素，一是距离污染源的位置，二是污染浓度场的不确定度.

图7为浓度场的不确定度随采样点数目的变化情况.从图中可以看出，随着采样点数目的增加，浓度场的不确定度随之降低，并且当采样点的数目增加至7时，浓度场的不确定度降到了较低的水平，为237.45（mg·L－1）2，即平均标准差为0.24 mg·L－1，已达到污染羽识别的精度要求，结束计算.

5 结论

（1）基于卡尔曼滤波技术和模糊集合理论提出一类地下水污染羽识别的方法，算例研究表明该方法是一种有效的污染羽识别算法，能够以尽可能少的采样点确定污染源的位置，并较为准确地达到识别污染羽的目的.

（2）该方法应用了污染浓度场库的概念，只需要在计算开始时利用数值模型生成多个浓度场，此后的计算中不需要重新计算浓度场，节省了计算成本.

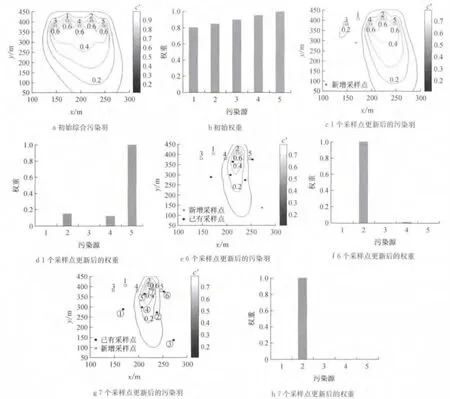
图6 综合污染羽与污染源权重随采样的变化Fig.6 The change of composite plume and its source location weights with sampling

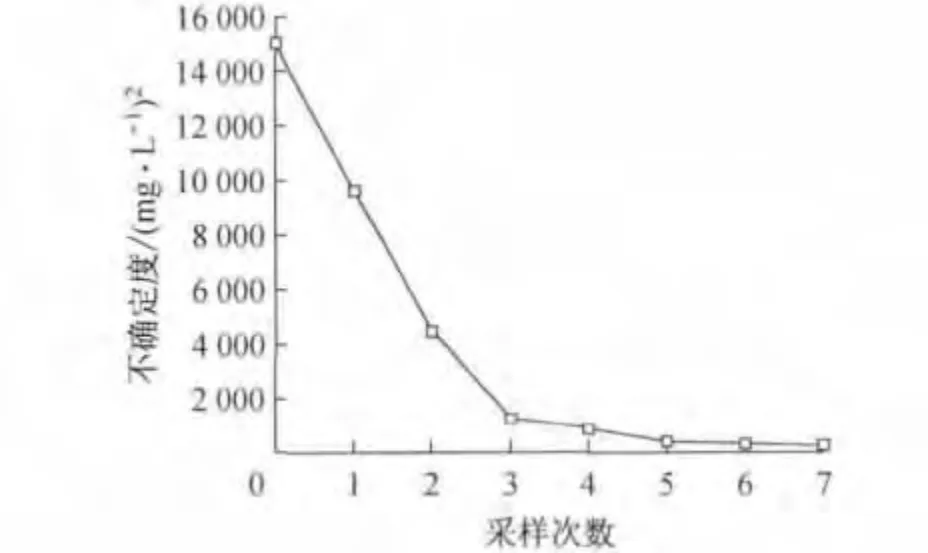
图7 不确定度随采样次数的变化Fig.7 Convergence of uncertainty with the procedure of sampling

（3）所建立的污染羽识别方法目前只是考虑了渗透系数的不确定性，并且污染源的强度假设是已知的.在下一步的研究中要考虑其他水文地质参数的不确定性影响下污染源的位置和强度的同步识别.

［1］ 吴剑锋，郑春苗.地下水污染监测网的设计研究进展［J］.地球科学进展，2004，19（3）：429.WU Jianfeng，ZHENG Chunmiao.Contaminant monitoring network design：recent advances and future directions ［J］.Advance in Earth Sciences，2004，19（3）：429.

［2］ Chien C C，M A Medina，G F Pinder，et al.Environmental modeling and management：theory，practice and future directions［M］.［S.l.］：Today Media Inc，2002.

［3］ Wu J，Zheng C，Chen C C.Cost－effective sampling network design for contaminant plume monitoring under general hydrogeological conditions ［J］.Journal of Contaminant Hydrology，2005，77（1／2）：41.

［4］ Dhar A，Datta B.Global optimal design of ground water monitoring network using embedded Kriging ［J］.Ground Water，2009，47（6）：806.

［5］ Owlia R R，Abrishamchi A，M Tajrishy.Spatial－temporal assessment and redesign of groundwater quality monitoring network：a case study ［J］.Environmental Monitoring and Assessment，2011，172（1／4）：263.

［6］ Datta B，Chakrabarty D，Dhar A.Optimal dynamic monitoring network design and identification of unknown groundwater pollution sources［J］.Water Resources Management，2009，23（10）：2031.

［7］ Kim K，Lee K. Optimization of groundwater－monitoring networks for identification of the distribution of a contaminant plume ［J］.Stochastic Environmental Research and Risk Assessment，2007，21（6）：785.

［8］ 王开丽，黄冠华.二维强非均质含水层中渗透系数空间变异对污染物迁移的影响［J］.水利学报，2010，41（4）：437.WANG Kaili， HUANG Guanhua. Effect of hydraulic conductivity on contaminant transport in highly heterogeneous two－dimensional aquifers［J］.Journal of Hydraulic Engineering，2010，41（4）：437.

［9］ 阎婷婷，吴剑锋.渗透系数的空间变异性对污染物运移的影响研究［J］.水科学进展，2006，17（1）：29.YAN Tingting，WU Jianfeng.Impacts of the spatial variation of hydraulic conductivity on the transport fate of contaminant plume［J］.Advances in Water Science，2006，17（1）：29.

［10］ 施小清，吴吉春，吴剑锋，等.多个相关随机参数的空间变异性对溶质运移的影响［J］.水科学进展，2012，23（4）：509.SHI Xiaoqing，WU Jichun，WU Jianfeng，et al.Effects of the heterogeneity of multiple correlated random parameters on solute transport［J］.Advances in Water Science，2012，23（4）：509.

［11］ Herrera G S，Pinder F G. Space－time optimization of groundwater quality sampling networks［J］.Water Resources Research，2005，41（12）：407.

［12］ Dokou Z，Pinder F G.Optimal search strategy for the definition of a DNAPL source［J］.Journal of Hydrology，2009，376：542.

［13］ Remy N，Boucher A，Wu B J.Applied geostatistics with SGeMS：a user’s guide［M］.New York：Cambridge University Press，2009.

［14］ 吴剑锋，彭伟，钱家忠，等.基于INPGA的地下水污染治理多目标优化管理模型：I——理论方法与算例验证［J］.地质论评，2011，57（2）：277.WU Jianfeng，PENG Wei，QIAN Jiazhong，et al.INPGAbased multi－objective management model for optimal design of groundwater remediation system：Ⅰ—methodology and its experimental validation ［J］.Geological Review，2011，2：277.

［15］ 刘胜，张红梅.最优估计理论［M］.北京：科学出版社，2011.LIU Sheng，ZHANG Hongmei.Theory of optimal estimation［M］.Beijing：Science Press，2011.