基于贝叶斯克里金的地下空间多源数据建模

李晓军，李培楠，朱合华，刘 俊

（1.同济大学 土木工程学院，上海 200092；2.同济大学 岩土及地下工程教育部重点实验室，上海 200092；3.同济大学 测绘与地理信息学院，上海 200092）

随着地下工程信息化水平的不断提高，三维地质建模技术在地下工程中得到越来越多的应用［1］.借助成熟的三维地质建模技术和软件，建立描述地质体的形态特征和构造要素空间关系的地下工程三维地质模型，不仅能全面地描述研究区域地层的空间几何形态及其相互关系［2］，还能为地质体边界限定、资源评估、地下构建筑物的规划、隧道或巷道开挖以及后期的力学分析提供帮助［3］.为了减少地质模型的不确定性，应集成和融合多种地质勘探数据，如钻孔、地质剖面以及矿业生产中的各种等高线信息来建立更加准确的地质模型［4］.传统的多源地质建模方法主要是基于钻孔、剖面和地形地质图等数据采用地质统计学来建立地质模型［5］.例如Martelet等［6］利用钻孔、剖面以及断层边界范围数据来推断地质界面并建立模型；Wu等［7］针对地质数据大多比较稀疏和低采样率的特征，提出逐步细分的多源数据集成建模方法，对初始地质模型不断修正；钟登华等［8］利用多源地质数据建立了水利水电工程坝区的三维地质模型.上述研究将各种不同来源的信息离散化，在插值和建模时进行硬合成，实现多源信息的集成，以提高模型的精确度.然而上述方法的问题在于未考虑各种地质数据的不确定性差异，因而无法准确评价估计结果的不确定性.

为了更有效地利用不同类型和质量的地质数据，并保证其在地质建模过程中的一致性，本文以矿业生产为背景，考虑地质数据的不确定性程度，把勘探数据分为硬数据（如钻孔、露头和开挖信息）和软数据（如剖面、地震、地质解译图件和专家经验等）［9］，利用区域变量理论研究这2类信息的空间结构变化特征，并采用贝叶斯克里金（BK）方法集成2种不同类型的数据来估计煤层表面高程，据此建立煤层三维地质模型，并通过与普通克里金（OK）方法的比较对该方法的正确性和有效性进行了验证.

1 基于贝叶斯克里金方法的煤层建模

1.1 贝叶斯克里金基本原理

用z（x）表示区域D上的一个区域性变量，相应的随机函数记为｛Z（x），x∈D｝，在这里Z（x）代表观测数据所对应的随机函数，简称硬数据；用M（x）表示区域D上的另一个区域性变量，相应的随机函数记为｛M（x），x∈D｝，这里的M（x）代表猜测数据，简称软数据.

假定随机函数Z（x），x∈D 的一组观测集［Z（xi），i＝1，2，…，N］.由此定义一个随机函数为

式中：μM（x）为 M（x）的数学期望值.对任意一组观测值｛ZT（xi）＝Z（xi）-μM（xi），i＝1，2，…，N｝，BK估计希望得到的估计值Z＊（x0）具有如下形式：

式中：x0为区域D 中一点；λi（i＝1，2，…，N）为待定的加权系数.

依据估计的无偏性和估计方差的最小性，利用拉格朗日方法得到关于权系数λi的BK方程组.

通过求解BK方程组，可以得到λi和β值.求得λi后，还可以进一步求得最小的估计误差方差，即BK方差.

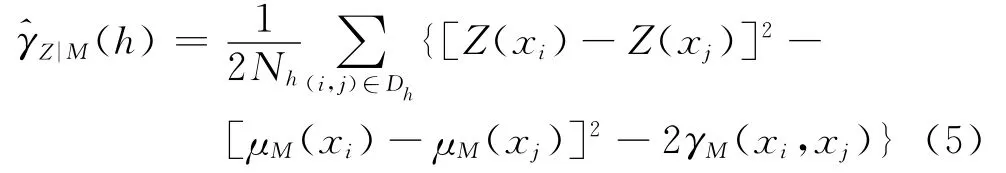
式中：Nh为数据对的个数，h为不同数据点之间的空间分离距离.γM（xi，xj）不仅依赖于xi和xj之间的距离，还依赖于它们本身的位置.因此，它应该从更大的一类函数族中去选取.Omre［10］证明了当取有如下形式时，它是条件正定的.

式中：σM（x）是定义于D 上的非零函数；γS（·）为标准的变异函数形式，且［1-γS（xi-xj）］是正定函数.上式还可以改写成

式中：CS（xi-xj）＝1-γS（xi-xj）.CS（·）可以看成是一个空间相关函数，由于通常假设｛M（x）；x∈D｝的一、二阶矩是已知的，因此（x）就是软数据的方差（不确定性的定量表示）.如果软数据的（x）在整个区域D内是常量，那么这种情况就可以简化成基于随机残余函数｛ZT（x），x∈D｝的普通克里金估计，也对应于减去预定义漂移的泛克里金方法.特别地，如果软数据中不含任何不确定量，即方差Var［M（x）］＝0，x∈D，则γZ（xi，xj）＝γZ｜M（xixj），这就退化到了简单克里金系统［11］.

1.2 数据网格化过程中的断层处理

当研究区存在许多断层时，构造非常复杂，在数据网格化的时候就要考虑到断层的影响.目前常用的方法主要有：分块法、断层恢复法、断面法、最小绕射距离权法和断层轨迹法.这些方法中，断层恢复法的效果较好且简便，其基本思想是将地质体恢复到没有被断层切割前的状态，对其直接插值，再叠加受断层影响所产生的局部位移，最终得到真实的地层或煤层面网格数据，过程如下.

（1）把零位移线和断层轨迹围成的区域看作是地层面的移位部分，其他部分作为非移位部分.根据零位移线和断层轨迹上的落差可以内插出在移位区域网格点上的落差值.非移位部分的网格点上的落差假定为零，由此得到垂直位移网格数据体.

（2）利用垂直位移网格数据把受断层影响区域附近的层位复原到断裂发生前的位置.用网格化的落差数据在位于地层面的移位部分的每个已知数据点上内插一个值，这个值可以认为是地层面在这一点上的落差.不在移位部分的每个数据点上的内插值为零.把所有的内插值从原始数据中减去就消除了由断裂引起的落差，这相当于得到地层断裂前的观测数据.显然，只有受断层影响的数据才被替换.

（3）建立复原层面的网格数据体.如果位移网格数据是正确的，即数据点处的层位已复原到断裂前的位置上，可用不考虑断层影响的常规网格化技术求得复原地层的网格数据体.即便某些断块上只有很少的观测数据或根本没有观测数据，也可以进行网格化，因为这时已没有断层的影响了.

（4）把落差网格和复原地层网格相加，即可得到实际地层的网格数据体.

2 煤层表面估计与结果分析

2.1 工程地质条件

以安徽淮南望峰岗煤矿地下采掘工程为背景，主要利用钻孔和地震数据建立煤层地质模型.该矿共含煤37层，平均总厚40.55m.其中，可采煤层共17层，主要可采煤层12层.井田含有38条断层，其中逆断层5条，正断层33条；落差大于等于100m的7条，100～50m的3条，50～30m的5条，落差在30m以下的23条.井田范围内总共有37层煤层，其平均总厚度为40.55m.考虑到煤层厚度、深度以及可持续开采程度的限制，可采煤层有11层，分别为：A1，A3，B4b，B6，B7，B9b，B10，B11b，C13和C15.井田勘测数据主要包括99个原始勘探钻孔，形成勘探剖面23个.每条勘探剖面上有相应的煤层分布信息，以煤层界面信息为主.

本文所建模型在勘探线VI以北地区，面积为3.6km×1.8km，其中共有30个钻孔数据、11条勘探剖面图以及11层煤层底板等高线图.其中煤层底板高程等值线是由地震勘探的解译信息推断所绘，地质剖面图是基于地震解译生成，并由钻孔数据修正.其中包含的信息主要有煤层与地层的交界面和断层线，在三维地质建模中将作为主要的约束信息参与地层模型的插值.其中，C13煤层以其良好的开采条件作为该煤矿的首采煤层，其中煤厚分布相对较平稳，在7～9m附近波动，且埋藏深度较浅.因此，以C13煤层底板高程来验证BK算法的可靠性.

2.2 基于贝叶斯克里金方法的煤层底板高程估计

硬数据是指在确切位置上的精确地质信息，如钻孔数据.软数据是指那些可能的或模糊的地质采样信息，如剖面图和底板等高线.这些原始的输入数据可以用如下3种类型的数学形式来表达：硬数据，Z（xi）＝Zi，其中Z（xi）为空间任意一点xi处的属性值；间隔型软数据，ai≤M（xi）≤bi；分布型软数据，Fxi（m）＝P ［M （xi）≤m ］，其中M（xi）为空间属性值所代表的随机变量，［ai，bi］为间隔型软数据的变化区间，Fxi（m）为分布型软数据的累积频率，P为概率分布.因此，不论是间隔型软数据，还是分布型软数据，都可以利用σM（x）表示地质信息的离散程度并对其不确定性进行编码.

为了合理地利用BK方法，在估计之前，地质剖面和地震等高线所代表的软数据需要离散化，考虑计算效率，其离散间距尺寸为200m×200m，而输出网格尺寸为20m×20m.以煤层C13底板高程数据为例，剔除部分C13煤层缺失的钻孔资料，其中可以利用的硬数据总数为26个，软数据总数为238个，共有264个软硬数据参与估计，软硬数据的空间分布情况如图1所示，其中，NW-SE表示西北-东南方向，SW-NE 表示西南-东北方向.

图1 投影到水平面上的数据空间位置Fig.1 Map of data locations projected onto a horizontal plane

表1给出了不同数据源下的C13煤层底板高程数据的整体概率统计指标.硬数据所代表的高程均值为-809.54m，而软数据所代表的高程均值为-931.09m.对比图1可看出钻孔主要分布在该图的中间偏上部位，这也与该处煤层深度较浅、方便钻井施工有关.通过高程的标准差和变化范围可以看出软数据具有较大的空间变异性和不确定性.

表1 高程的软硬数据统计指标参数Tab.1 Statistics for hard and soft data of coal floor elevation

为了求解BK线性方程组，需要建立2种变异函数模型，即利用软数据得到的变异函数模型和综合软硬数据的条件变异函数模型.由于变异函数的确定是求解BK方程的首要问题，而条件变异函数的获取首先需要得到软数据所代表的随机函数的数学期望，因此，首先利用一个倾向东北、倾角为25°的二阶多项式曲面方程来拟合软数据一阶矩μM（x）分布，其代表了软数据随位置不同而变化的期望函数，如图2所示.具体的软数据所代表的随机函数的期望函数μM（x）的二次曲面函数拟合公式为

图2 基于软数据的C13煤层底板高程云图等高线Fig.2 Map of C13coal seam floor elevation contours used as soft data for the model

求出了μM（x），还需要得到σM（x）（一般通过主观假设和专家经验获得），才能完整地求解γM（xi，xj），γZ｜M（xi-xj）以及BK 方程组，而对于该煤层地质模型，由式（6）和式（7）可以看出，剖面及地震数据的不确定性是通过在γM（xi，xj）中的σM（x）来体现的，σM（x）表达了不同位置处的剖面及地震数据的离散性，即不确定性.一般来说，由于地质剖面大多数依赖地质工程师的专家经验和钻孔之间的插值，地震数据解译过程中的速度迁移模型、时深转换以及分辨率等因素都会带来解译结果的不确定性，且深度越大不确定性越大，因此假定σM（x）随着深度线性增加，如表2所示.

表2 分配给特定深度处软数据的标准差Tab.2 Standard deviations assigned to the soft data

考虑到煤层在走向和倾向上的区域化变量的差异比较明显，因此建立各向异性的变异函数模型来对区域化变量的结构特征进行描述.这2个方向上的变异函数理论模型的参数是采用加权多项式回归方法来拟合采样变异函数所得到，最终通过交叉验证来选取最合适的理论变异函数模型及其参数［12］.以26个钻孔资料为验证数据源，以平均误差（ME）、均方差（MSE）、平均克里金方差（MKV）和标准化克里金方差（SKV）为统计学指标，其判断标准为：ME尽可能接近于零；MSE和MKV尽可能小，且两者尽量接近；SKV尽可能接近于1［12］.表3给出了变异函数各拟合模型指标参数的比较.

表3 理论变异函数模型的精确度评价Tab.3 The assessment on precision of theoretical model

通过计算，软数据的各向异性变异函数的套合结构模型（图3a）最终用球状模型描述，其中变异函数的块金值为542.5m2，基台值为1710.2m2，NW-SE方向变程为1611.988m，SW-NE方向变程为829.565m，各向异性比为1.95.软数据的各向异性变异函数结构套合模型为

集成软硬数据的条件各向异性变异函数模型（图3b）的块金值为5985m2，基台值为23488m2，NW-SE方向变程为1542.154m，SW-NE方向变程为873.043m，各向异性比为1.76.集成软硬数据的条件各向异性变异函数结构套合模型为

各向异性分离距离h的套合公式如下所示，其中hNW-SE为西北-东南的分离距离，hSW-NE为西南-东北的分离距离，K为各向异性比.

图3 各向异性变异函数模型Fig.3 Sample and modeled variogram along main anisotropy directions of normal

利用BK方法进行估计的C13煤层底板高程和估计标准差分布情况如图4所示.在加上了地震数据之后估计误差标准差在钻孔附近偏小，远离钻孔的地方标准差较大，不确定性在远离钻孔的研究区域底部和右上角达到最大.BK方法并不是把软数据简单地离散作为硬数据的补充.同时，在钻孔数据稀少的右下角区域，该等值线主要反映了地震数据的特征，由此认为，BK方法克服了钻孔数据过少带来的估计失真和外推精度较差的问题.

3 估计方法的比较与验证

3.1 估计方法的比较

为了探讨BK方法在集成多源数据上的优势，将BK估计结果与软数据直接离散化后加入硬数据中的OK估计结果进行比较，以ME，MSE和皮尔逊相关系数r作为评价指标，评价结果如表4所示.

同样，基于26个钻孔数据，此处的交叉验证法所得到的BK方法估计的结果与表3中球状模型的ME和MSE指标相同，这是因为本文通过球状变异函数模型来进行空间区域性变量的估计.然后，再利用这26个测量值与估计值之间的误差作频率直方图，其拟合曲线如图5所示.

图4 C13煤层底板高程BK估计结果Fig.4 The estimation map and standard deviation map in the coal seam C13obtained by BK procedure

表4 2种方法的整体定量比较标准Tab.4 Quantitative comparison criteria of these two methods in the overall area

图5 BK和OK的估计误差分布直方图Fig.5 Histograms of estimation errors for BK and OK

由表4可见，无论是平均误差还是均方误差，OK方法都比BK方法大，因此可以认为，相对于BK方法，OK方法估计值的不确定性更大.这是因为OK方法虽然简单地集成了软硬数据，但没有考虑软硬数据的不确定性程度区别，在软数据存在较大的测量、解译以及推断误差的情况下，即在深部地震解译信息的处理中，如果没有给出合适的误差波动范围，估计结果会和钻孔或开采巷道处的真实信息存在较大的偏差.由交叉验证生成的整体估计误差分布如图5所示.从图5中2条误差频率直方图拟合曲线可以看出，利用OK方法所产生的误差分布主要集中于［-11.25，13.75］，利用BK方法所产生的误差分布主要集中于［-7.00，9.00］，后者误差分布范围更集中.由此说明，OK估计方法会产生较大的误差离散程度，导致其不确定性更大，对于其估计结果的精确度更难控制.而BK方法能在较少硬数据的条件下，通过合理利用软数据作为补充，给出更为精确的估计结果.

3.2 估计方法的验证

为了更进一步验证BK方法的有效性，基于煤层开采中所获得的局部实测信息，即煤巷中的见煤点和地质素描数据，利用OK和BK方法分别进行对比验证.煤层估计值与实测值比较曲线见图6a，估计值与实测值之间的偏差见图6b.其中实测曲线由首采区工作面附近煤巷中的见煤点数据拟合而成，隆起部位是由于邻近区域内有钻孔.

图6 C13煤层底板高程不同估计方法的局部验证结果Fig.6 The validation of the estimation results about the coal seam C13

对比2条估计曲线（图6a），BK预测相对于OK预测更加接近于实际情况.OK方法把软数据当成硬数据，严格地通过每一个软数据点，由于在局部采区该深度范围内，相对于钻孔数据来说地震数据平均有2～3m的误差，因此把软数据直接作为硬数据的补充有一定的局限性，所产生的偏差比BK方法更大，其中OK方法平均偏差为0.72m，BK方法平均偏差为0.28m（图6b）.相反，BK方法对地震数据赋予一定的不确定性，并在估计中加以考虑，所得结果与实际值更加吻合.2种方法局部估计偏差的评价指标如表5所示.OK方法的平均误差和均方误差的绝对值都比BK方法大，因此同样可以认为，在局部尺度下BK方法相对于OK方法能够提供更加准确的估计结果.在隧道的两端，BK方法估计结果与真实值的相关程度更大，这表明在钻孔较稀少的区域，BK方法能结合地震数据得到更合理的外推结果.

表5 局部估计偏差的定量比较标准Tab.5 Quantitative comparison criteria of the discrepancies between the observations and the estimation in the local area

4 煤层三维模型的构建

由于C13煤层被4条大型断层（落差为15～30 m）、2条中型断层以及3条小型断层所切割，因此，在数据网格化过程中需要利用相应的断层处理技术来处理断层对空间变量的影响.即：①建立地层面的垂直位移网格；②用已得到的垂直位移数据对数据点作内插，使数据点处的层面复原到断裂发生前的位置；③用复原后的数据建立一个网格数据体；④把2个网格相加，即生成了考虑断层影响的网格数据体.本文采用BK方法完成步骤③之后，再加上由断层引起的垂直位移，最终通过约束Delaunay算法生成一系列不规则三角网，如图7所示.图8为最后利用煤层上下表面三角网的拓扑对应关系生成的煤矿区域三维地质模型.

5 结论

图7 C13煤层底板的不规则三角网Fig.7 A TIN mesh of C13coal floor surface

图8 3D煤层地质模型Fig.8 The 3Dgeological model of the coal seams

通过BK方法使钻孔数据和地震数据有机结合，而不是单纯从地震剖面上获取地层在平面各点处的深度，以此弥补了钻孔采样数据的不足.其估计结果在硬数据比较稀少的地区主要反映了软数据的特征，而在硬数据比较稠密的地区主要取决于硬数据.该方法不仅有效地集成了钻孔和地震数据，还克服了稀少钻孔数据的外推缺陷.通过与把软数据直接硬化后加入待估数据集的OK方法进行对比，BK方法在合理利用软硬数据方面具有的优越性和合理性表现如下：

（1）地震深度数据是描述地质体空间分布特征的信息，它在反映地层界面在一个地区的整体变化趋势方面具有比较好的效果，但就局部范围而言，其精度又较差，因此把这2类数据不加区别地混合在一起使用，必然会造成较大的误差.

（2）与OK方法相比，BK方法能够得到更小的平均误差和均方误差，所以在集成大范围精度较差的地震数据工作中BK方法能够给出更加令人满意的结果.

（3）BK方法的优势在于能够集成直接观测信息和含有不确定性的全局性先验信息，利用σM（x）合理地分配软数据的全局不确定性，并基于γM（xi，xj）在插值过程中进行计算.在观测点密集的区域，直接观测数据对其计算结果的影响较大，而在远离观测集的区域内，软数据及其不确定性σM（x）对最终计算结果也有显著的影响.因此BK方法给出的估计结果更加符合地质数据的实际情况，且在钻孔数据稀少且存在非精确地震数据作为补充的情况下具有较为广阔的应用前景.

［1］陈学习，吴立新，车德福，等.基于钻孔数据的含断层地质体三维建模方法［J］.煤田地质与勘探，2005，33（5）：5.CHEN Xuexi，WU Lixin，CHE Defu，et al.3D modeling method of geological bodies including faults based on borehole data［J］.Coal Geology ＆Exploration，2005，33（5）：5.

［2］姜在炳.煤层动态建模技术及应用［J］.煤炭学报，2006，31（1）：40.JIANG Zaibing.Dynamic modelling technology of coal seam and its application［J］.Journal of China Coal Society，2006，31（1）：40.

［3］Caumon G，Collon-Drouaillet P，le Carlier de Veslund，et al.Surface-based 3D modeling of geological structures ［J］.Mathematical Geosciences，2009，41（8）：927.

［4］Kaufmann O， Martin T.3D geological modelling from boreholes，cross-sections and geological maps，application over former natural gas storages in coal mines［J］.Computers ＆Geosciences，2008，34（3）：278.

［5］李晓军，胡金虎，朱合华，等.基于Kriging方法的煤层厚度估计及三维煤层建模［J］.煤炭学报，2008，33（7）：765.LI Xiaojun，HU Jinhu，ZHU Hehua，et al.The estimation of coal thickness based on Kriging technique and 3D coal seam modeling［J］.Journal of China Coal Society，2008，33（7）：765.

［6］Martelet G，Calcagno P，Gumiaux C，et al.Integrated 3D geophysical and geological modelling of the Hercynian Suture Zone in the Champtoceaux area（south Brittany，France）［J］.Tectonophysics，2004，352：117.

［7］Wu Q，Xu H，Zou X.An effective method for 3D geological modeling with multi-source data integration［J］.Computers ＆Geosciences，2005，31（1）：35.

［8］钟登华，李明超，杨建敏.复杂工程岩体结构三维可视化构造及其应用［J］.岩石力学与工程学报，2005，24（4）：575.ZHONG Denghua，LI Mingchao，YANG Jianmin.3D visual construction of complex engineering rock mass structure and its application［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（4）：575.

［9］高美娟，朱庆忠，张淑华.利用贝叶斯-克里金估计技术进行储层参数预测［J］.石油地球物理勘探，1999，34（4）：390.GAO Meijuan，ZHU Qingzhong，ZHANG Shuhua.Reservoir parameter prediction using Bayesian kriging estimation technique［J］.Oil Geophysical Prospecting，1999，34（4）：390.

［10］Omre H.Bayesian kriging merging observations and qualified guesses in kriging［J］.Mathematical Geology，1987，19：25.

［11］Nobre M M，Sykes J F.Application of Bayesian kriging to subsurface characterization［J］.Canadian Geotechnical Journal，1992，29（4）：589.

［12］张仁铎.空间变异理论及应用［M］.北京：科学出版社，2005.ZHANG Renduo.The theory and application of spatial variability［M］.Beijing：Science Press，2005.