海上风电机组单桩基础模态及参数敏感性分析

靳军伟，杨 敏，王 伟，王其标

（1．同济大学 土木工程学院，上海200092；2．同济大学 岩土及地下工程教育部重点实验室，上海200092；3．上海同济启明星科技发展有限公司，上海200092；4．中交上海三航科学研究院有限公司，上海200032）

风能源已经逐渐成为取代传统能源发电的一种主要形式，具有无污染、可再生等特点，是一种取之不尽、用之不竭的新能源．根据世界风能源协会2012年上半年的统计报告［1］，中国在2012年上半年新增风能源5．4GW，总装机容量达到67．7GW，继续保持世界最大风电市场并拥有全球最大的总装机容量．中国风电场主要为西部地区的陆上风电场和东部沿海地区的海上风电场．对于海上风电机组来说，其基础设计至关重要，是保证风机稳定运行的关键技术之一，投资造价也接近工程投资的30%．基础不仅要满足构件强度、变形及稳定性等静力方面的要求［2］．由于受到风、海浪等随机动力荷载，还需要考虑动力方面的影响，而模态分析是进行动力分析的基础，其计算的正确与否直接影响风机系统的正常使用以及风电机组的使用寿命［3－4］．

关于风电机组的模态分析，国外曾进行了大量的试验，主要为风机叶片以及塔筒构件等方面．文献［5］进行了桶形基础风机的模态测量，并验证了采用不同数值模型计算的合理性．文献［6］通过对风机叶片的模态特性的检测分析了裂缝对叶片模态的影响．文献［7］采用点跟踪视频测量技术对大型风机结构进行了模态分析．但是通过试验模态进行分析，测量过程复杂，数据采集量大，且对于基础结构而言，场地条件复杂，对于实际设计中的大型风电项目较难实现．相比较而言，可以通过动力模态基本理论得到风机系统的模态参数，文献［8］采用ANSYS 软件，将风机塔筒简化为壳单元，分析了风机的模态，并验证了忽略塔筒底部门道时，计算模型的合理性，但是其并没有考虑下部基础对风机塔筒的影响．上述研究并没有进行风电机组整体的模态分析，同时也没有系统地考虑关键的设计参数对海上风电系统的模态的影响，而这些方面对风机体系来说十分重要．

本文在考虑桩土相互作用的基础上，同时考虑基础的存在对风机系统的影响，基于里兹直接叠加法计算得到单桩基础的9阶模态，并进行关键设计参数敏感性分析．

1 模态设计

海上风电机组所受的动力荷载中的风荷载为最重要的荷载，推动叶片转动，叶片转动对风机系统的激励频率可以分为2种［9］，首要的激励频率为单个叶片的额定转动频率，即1P，其次为NbP，其中Nb为风机叶片的个数．以该频率为基础，可以将风机体系的设计分为柔－柔、刚柔、刚－刚3 类，以避开不利频率．

基础设计为柔－柔形式的基础如悬浮式基础，基础设计为柔－刚形式的基础诸如三脚架、四脚架等基础，基础设计为刚－刚形式的基础如重力式基础等．基础整体刚度越大，则基础工程量越大，投资也会增大．而柔－柔结构则由于频率距离海浪频率过近可能造成较为严重的疲劳损伤．当将柔－刚结构作为海上风电系统的方案时，对于3叶片风机机组，一般需要在风机1P～3P频率之间进行设计，此时对设计要求十分苛刻．

2 公式

2．1 原理

对于多自由度体系来说，其每个自由度方向上自振频率和振型可通过求解系统的动力方程（1）得到：

式中：K为系统刚度矩阵；φ为振型；ω为自振频率；M为系统质量矩阵．

对于大型结构，一般仅求解与激励荷载频率范围相关的前n阶振型．计算方法［10］主要有子空间迭代法、兰佐斯法、里兹向量直接叠加法等．本文以里兹向量直接叠加法为计算手段．

2．2 里兹向量直接叠加法

里兹向量直接叠加法［10－11］是根据载荷空间分布模式按一定的规律生成1组里兹向量，在将系统运动方程转换到这组里兹向量空间后，只要求解1 次缩减了的标准特征值问题，再转回原系统向量空间，就可得到原系统运动方程的部分特征解．

系统的质量矩阵为M、刚度矩阵为K，同时假定单位荷载矩阵为Q（s，t）．

式中：s为空间坐标；t为时间；F（s）为荷载的矢量矩阵，F（s）对所计算的自由度均设置单位矢量；q（t）为t时刻的荷载．将刚度矩阵三角化得

式中：D为对角矩阵；L为单位上三角矩阵．

考虑到Euler梁单元［10］在不考虑剪切变形的情况下计算结果不精确，本文中风机塔筒及桩体的刚度矩阵均采用Timoshenko梁单元［10］进行计算．

计算第1个里兹向量x1，求解方程

计算其余n－1 个里兹向量（n为所需的阶数，n＝9）．由计算为新迭代步计算得到的迭代向量．为了保证结构的前n个特征解有足够的精度，r取所需计算模态阶数的2倍［10］．

得到

求解上式特征值问题，得到特征解Φ＊和Ωr．由Φr＝XΦ＊即可得到原始系统的频率与振型．

2．3 桩土相互作用

作为基础结构，基桩与土体之间的相互作用是需要解决的重要问题，本文水平向桩土之间以及桩侧与桩端竖向的桩土相互作用采用线性弹簧来描述，如图1所示．水平向桩土相互作用采用m法［12］来描述，弹簧刚度通过m值（桩侧地基土水平抗力系数的比例系数）与单位长度桩体竖向截面的乘积得到．桩侧与土之间竖向的相互作用也采用线性弹簧，桩侧摩阻力的大小采用美国石油协会所推荐的荷载－位移（t－z）曲线形式［13］，如图2所示，图中t为桩侧摩阻力发挥值，tmax为桩侧摩阻力发挥最大值，z为桩土相对位移，D为桩身直径，f为根据经验公式或工程实测得到的桩侧摩阻力最大值，tres为桩侧摩阻力残余值．需要注意的是，黏土中桩侧摩阻力的发挥与D有关，即横坐标为z／D．而砂土中应力水平的发挥仅与桩土之间的相对位移有关，为了简化计算，弹簧刚度均取拐点之前的割线模量，计算取值可参考与图2所对应的表1中的数据．

图1 桩－土简化示意Fig．1 Load and soil spring profile

图2 桩侧荷载－位移曲线［13］Fig．2 Pile load transfer－displacement curves［13］

对于桩端弹簧，通过桩端荷载的大小与极限端阻力之间的相互关系得到弹簧的力－位移的对应关系．如图3所示，采用美国石油协会［13］所推荐的荷载－位移（Q－z）曲线（量纲为一），弹簧刚度采用Q－z曲线拐点之前的割线模量，计算取值可参考与图3所对应的表2中的数据，其中Q为桩端土体承载力发挥值，Qpmax为桩端承载力极限值．

表1 桩侧荷载－位移关系［13］Tab．1 Pile load transfer－displacement t－z relationship［13］

图3 桩端荷载－位移曲线［13］Fig．3 The pile tip load－displacement curve［13］

表2 桩端荷载－位移曲线数据［13］Tab．2 Data about the pile tip load－displacement［13］

3 算例

3．1 基本参数

3．1．1 风机系统参数

以渤海湾乐亭风电场所采用的风机为例，风机叶片长50．3m，叶轮直径105．0m，塔架距轮毂中心高度90．0m，设计使用寿命为20年，风机切入风速为3 m·s－1，切出风速为25 m·s－1，额定风速为12．5m·s－1，叶轮扫风面积为8 443m2．风轮1P为0．108～0．265Hz，3P为0．324～0．795 Hz．风机主要部分质量即风轮和机舱总质量为193t，重心位于塔筒顶部法兰向上1．86m、塔筒轴线向前1．15m．风机塔筒从上至下共分4节，变直径3．07～4．70m，壁厚19～52mm，塔筒总长度87．2m，如图4．

图4 风机及基础结构Fig．4 Wind turbine and the monopile foundation

基础为单桩基础，连接塔筒及桩的套筒构件采用变截面设计，自上而下直径为4．7～5．8 m，长15．5m，壁厚75mm．桩体直径5．5m，长68m，壁厚58mm，桩体上部采用灌浆套筒方法处理，以增强桩体的整体刚度．

3．1．2 土层参数

该风机所在地的土层参数如表3 所示，主要用于计算弹簧参数，按前述桩土相互作用方法，水平向采用m法，竖向采用t－z曲线法，底端采用Q－z曲线法．其中m值的选取依据《建筑桩基技术规范》［12］（JGJ94 2008）并依据工程经验对上部3 层土体的m值进行折减得到．t－z曲线法中桩侧极限摩阻力tmax根据工程所提供的勘察报告选取．Q－z曲线法中的桩端极限承载力Qp根据勘察报告提供的数据根据《建筑桩基技术规范》［12］（JGJ94 2008）钢管桩桩端竖向承载力计算方法得到．算例中Qp＝3 768kN．

表3 土层参数Tab．3 Soil layer parameters

3．2 计算结果

通过里兹向量直接叠加法得到单桩机组基础的频率和振型，如图5 所示，其中频率的阶数采用fx表示，x表示第x阶．由于风机机舱部分的偏心作用，频率在相互垂直的2个方向出现时稍有差别，但形态一致．除图5d扭转振型单独出现外，其他振型皆成对出现，且方向正交，图5中成对出现的振型仅列出1个．

图5 单桩模态振型Fig．5 Monopile modal

从前述风机系统参数判断，为了避开叶片的转动频率，风机需要满足的频率范围为0．265～0．324 Hz，工程所处海区的波浪频率为0．083～0．238Hz，为了保证计算的适用性，工程中通常取安全系数为1．05，即要求设计模型的频率范围为0．278～0．309 Hz．

图6所示非共振频率范围为区域①，②，③，风机位于区域②，可以很好地避开叶片工作频率1P和3P以及海浪的波动频率，且满足通常设计要求的安全系数．

从图6也可以看出，对于海上风电机组基础设计来说，要避开海浪的频率以及风机叶片的工作频率是十分困难的，所拥有的选择空间极其有限，从而造成对设计参数选取的经验性要求很高．

图6 风机共振判断Fig．6 Resonance judgement

4 参数影响分析

为了探讨各个设计参数对风机模态的影响，对设计参数进行敏感性分析．

由图6可知，单桩风电机组的3 阶频率一般偏离3P较远，故以下内容主要针对1～2阶频率进行分析，除特别指出外，以下部分的频率均指1～2阶频率．

4．1 套筒厚度

套筒是连接塔筒和下部桩基础之间的关键部位，其作为媒介使塔筒和基础形成一个整体，其具体位置参考图4．

由图7可见，随着壁厚增大，系统自振频率逐渐增大，最小频率没有低于设计的频率下限fmin（fmin＝0．278Hz），且第1，2阶频率十分接近．

图7 套筒厚度对频率的影响Fig．7 Influence of sleeve thicknesses on frequency

4．2 土层参数

4．2．1 水平向

不同地区的土层参数千差万别，其对风机模态的影响程度决定关键设计问题及设计思路．

土体水平向参数主要指土体的m值，由图8可见，m值的调整系数分别为0．6，0．8，1．0，1．2，1．4．由分析可知，随着m取值的增大，频率逐渐增大．最小频率在调整系数为0．6时已明显低于fmin，不能满足设计要求．由于m值的变化主要改变桩体的约束状态，且约束的发挥需要一定的桩体埋深，故并没有表现出线性关系，呈现出一定的非线性．

图8 水平土层参数对频率的影响Fig．8 Influence of horizontal soil parameters on frequency

4．2．2 竖向

土体竖向参数主要指土体的极限侧阻力．由图9可见，桩侧摩阻力的调整系数值分别为0．6，0．8，1．0，1．2，1．4．由分析可知，桩侧摩阻力值的变化对各阶频率没有影响．主要原因是前2阶振型主要为水平弯曲振型，并未出现竖向的压缩振型．

图9 竖向土层参数对频率的影响Fig．9 Influence of vertical soil parameters on frequency

4．3 桩

桩基础作为上部风电机组的主要承载构件，是设计中的关键部分．

4．3．1 壁厚

由图10可见，频率随着壁厚的增大而增大．桩基壁厚增大，桩体的刚度明显增大，从而导致系统频率增大．在桩体壁厚为48 mm 时，频率已明显低于fmin，不能满足设计要求．

图10 桩壁厚对频率的影响Fig．10 Influence of pile thicknesses on frequency

4．3．2 桩径

由图11可见，频率随着桩径的增大而增大．最小频率在桩径5．3 m 及5．4 m 工况下已明显低于fmin，不能满足设计要求．从刚度方面考虑，增大桩径的效果大于增大桩体壁厚的效果．

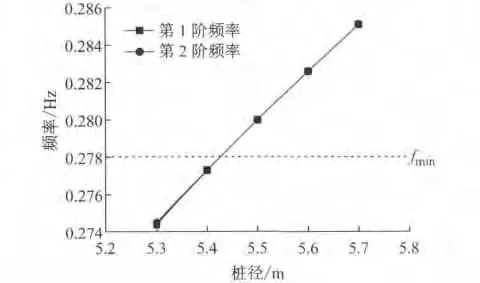
图11 桩径对频率的影响Fig．11 Influence of pile diameters on frequency

4．3．3 悬臂长度

桩体的悬臂长度，即位于海水中的长度，主要取决于海水深度．由图12可见，随着桩悬臂长度的增加，单桩模态频率逐渐减小，且变化幅度比较明显．最小频率在悬臂长度为31．5m 及36．5m 工况时低于fmin，不能满足设计要求，设计中需要避免出现该状况．

4．3．4 埋深

桩体的埋深主要基于桩基竖向、水平荷载大小以及桩基承载力进行设计．土体对桩的约束作用随着桩的埋深增加而逐渐增加，表现在模态方面，风电机组系统的频率也逐渐增加，且表现出明显的非线性关系，如图13所示，并在一定的深度趋于稳定．对于本算例，在桩体埋深37．5m 处，频率稳定为0．280 Hz．

图12 桩悬臂长度对频率的影响Fig．12 Influence of pile cantilever lengths on frequency

图13 桩埋深对频率的影响Fig．13 Influence of pile embed depths on frequency

通常情况下，在满足风机竖向和水平向承载力的条件下，桩体埋深一般接近临界深度，且在该条件下通过调整桩体埋深来改变系统频率很不经济，故对于实际工程，建议通过调整其他参数来达到相同的效果．

4．4 敏感性对比

为了对比各个参数的调整对频率的影响程度，将分析数据按照参数调整1%时计算对应的频率变化率，由于桩体埋深并不如其他参数显现出线性规律，故不参与对比分析．

从图14中可以看出，当套筒壁厚、m、桩壁厚参数取值调整为1%时，单桩风电机组系统的频率变化小于10%，可以认为上述参数对频率影响效果一般；桩悬臂长度每增加1%，频率变化接近20%，影响效果明显，需要注意的是，随着悬臂长度的增加，系统自振频率逐渐减小；对频率影响最为显著的为桩体直径，当桩径变化1%时，频率变化超过50%，为各调整参数对应的频率变化的最大值．由此可见，在设计中调整最有效的参数为桩径，其次为桩悬臂长度，再次为桩壁厚．

图14 不同参数对频率变化率的影响Fig．14 Influence of different member unit rates on frequency

5 结论

通过对海上风电机组基础的模态设计原理及其计算方法的研究，在考虑桩土相互作用条件下，采用里兹向量直接叠加法得到了海上风电机组单桩基础的9阶模态，并通过对套筒、土层、桩等关键设计因素进行参数分析得到以下结论：

（1）模态分析是海上风电机组基础设计中的重要环节，精确的基础设计可以有效地避开海浪频率以及风机叶片的共振1P～3P频率．

（2）单桩风电机组模态设计时，由于风机系统3阶及以上高阶频率部分高于风机工作时的转动3P频率，所以应主要考虑第1、第2阶频率的影响．

（3）单桩风电机组基础第1、第2阶频率随着套筒壁厚、m值、桩体壁厚、桩径的增大而增大，随桩悬臂长度的增大而减小．

（4）竖向压缩振型为高阶振型，竖向土层特性对前2阶弯曲振型没有影响．

（5）桩径对单桩风电机组基础第1、第2阶频率影响最为显著，直径变化1%将导致超过约50%的频率变化．工程设计中可首选对该参数进行调整，有效地避开对风机系统不利的频率．

（6）桩体埋深对单桩风电模态的影响存在一个临界深度，小于该临界深度时，频率随着埋深的增大而增大，超过该深度之后，风电机组基础的频率将趋于稳定．

［1］ The World Wind Energy Association．The World Wind Energy Association—2012 half year report［R／OL］．［2012－12－15］www．wwindea．org／webimages／Half－year＿report＿2012．pdf，2012．

［2］ 王国粹，王伟，杨敏．3．6 MW 海上风机单桩基础设计与分析［J］．岩土工程学报，2011，33（增2）：95．WANG Guocui，WANG Wei，YANG Min．Design and analysis of monopile foundation for 3．6 MW offshore wind turbine［J］．Chinese Journal of Geotechnical Engineering，2011，33（S2）：95．

［3］ 王伟，杨敏．海上风电机组基础结构设计关键技术问题与讨论［J］．水利发电学报，2012，31（6）：242．WANG Wei，YANG Min．Research and discussion of critical technology in the process of offshore wind power foundation design［J］．Journal of Hydroelectric Engineering，2012，31（6）：242．

［4］ American Burean of Shipping．Guide for the fatigue assessment of offshore structures［S］．Houston：American Bureau of Shipping，2010．

［5］ Lars Bo Ibsen，Morten Liingaard．Prototype bucket foundation for wind turbines natural frequency estimation［R］．Aalborg：Aalborg University，2006．

［6］ Ganeriwala N S，Yang J，Richardson M．Using modal analysis for detecting cracks in wind turbine blades［J］．Sound ＆Vibration，2011（5）：10．

［7］ Oliver Erne，GOM GmbH Mittelweg．Developments in large wind turbine modal analysis using point tracking videogrammetry［C］∥Proceedings of the IMAC－XXVIII．Jacksonville：Society for Experimental Mechanics Inc，2010：187－198．

［8］ CHEN Jie，JIANG Dongxiang．Modal analysis of wind turbine tower［C］∥World Non－Grid－Connected Wind Power and Energy Conference．Nanjing：［s．n．］，2010：1－3．

［9］ Jan van der Tempel，David－Pieter Molenaar．Wind turbine structural dynamics—a review of the principles for modern power generation，onshore and offshore［J］．Wind Engineering，2002，26（4）：211．

［10］ 王勖成．有限单元法［M］．北京：清华大学出版社，2003．WANG Xucheng．Finite element method［M］．Beijing：Tsinghua University Press，2003．

［11］ Dynamic analysis by direct superposition of rize vectors［J］．Earthquake Engineering and Structural Dynamics，1982（10）：813．

［12］ 中华人民共和国住房和城乡建设部．JGJ94 2008建筑桩基技术规范［S］．北京：中国建筑工业出版社，2008．Ministry of Housing and Urban－Rural Development of the People’s Republic of China．JGJ94－2008 Technical code for building pile foundations［S］．Beijing：China Architecture ＆Building Press，2008．

［13］ American Petroleum Institute． Recommended practice for planning，designing and constructing fixed offshore platforms—working stress design［S］．Washington D C：American Petroleum Institute，2007．