一类与算子有关的级数转化公式*

赵熙强，赵 芳

（中国海洋大学数学科学学院，山东 青岛 266100）

Heaviside积分是现在算子理论研究的基础。1973年G C Rota对算子理论进行了进一步的完善，尤其是同构定理［1］指出级数组成环与位移不变算子形成的环之间存在同构。根据这个同构定理T X He等人做了一系列的研究［2－5］，文献［2］中研究了算 子 （1－xE）－1的4种幂级数展开形式，并利用得到的结论加快了幂级数的收敛速度。2007年他们又对上述结论进行了推广［5］，研究了算子g（xE），并利用算子间关系得到了一类级数转化公式。将算子理论与Sheffer多项式联系起来也可以得到相应的级数转化公式，这类级数转化公式在研究一些特殊多项式性质及组合恒等式证明方面有重要应用。例如文献［5］中式（3.1），令f（k）＝kr，g（x）＝Ln（x），其中Ln（x）为Laguerre多项式，得

本文主要研究了算子g（xΔ）的幂级数展开形式以及由此得到的不同于前者的一类级数转化公式，第3部分给出了一些例子，用来说明转化公式的应用。

常见算子定义如下

算子间满足如下关系

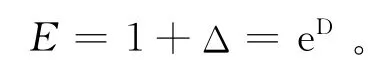
如果算子T可以和所有位移算子交换，即TEa＝EaT，其中a为任意实数，则T称为位移不变算子。

如果位移不变算子Q，满足Qx＝c，其中c为非零常数，则Q称为δ－算子。显然，微分算子D、差分算子Δ、位移算子Ε均为位移不变算子，而微分算子D为δ－算子。

证明 由第一展开定理［1］，Εk为位移不变算子，微分算子D为δ－算子，且其基础集为 ｛xn｝ ，故

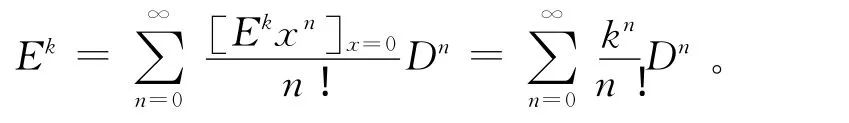
另外，为了能简化下面的级数转化公式，引进1个类似Euler多项式的1个新多项式。

其中g（y）有任意阶导数。

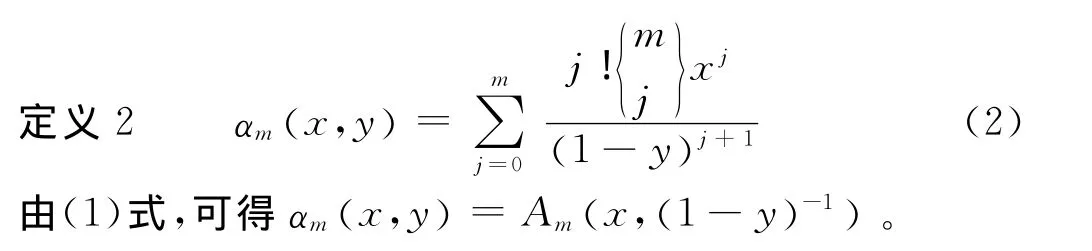
1 级数转化公式

利用级数转化公式可以得到很多组合恒等式，下面给出2个完全不同的级数转化公式。

其中：｛f（k） ｝为数列；g（x）和h（x） 在 ［0，＋ ∞）上有任意阶导数，Ak（x，g（0）） 定义如（1）。

证明 将g（xΔ） 作用于f（t） ，并在x＝0处展开，得

关于左边

类似的，对于任意阶可导的函数h（t） ，结合（3），令f（k）＝jk，有

由式（4）、（5）成立。

在（3）式中，g（x） 取不同的函数，可以得到很多有用的组合恒等式。

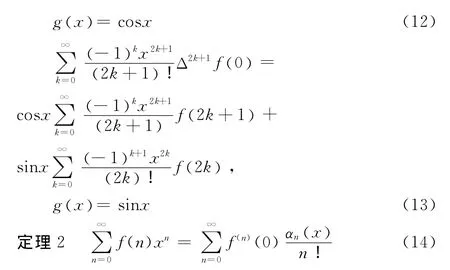
其中：αn（x） 为定义1.2中x＝y的情形；｛f（k） ｝为数列。

由式（15）、（16）即证。

2 应用举例

例1 在式（11）中令f（k）＝w（k＋1），w（k）为Bell数，式（11）变为

在上式中比较等式2边xm的系数，得

例2 在 式 （9）中，令f（n）＝s（n＋ 1，k） ，其 中s（n，k） 为第二类Stirling数.

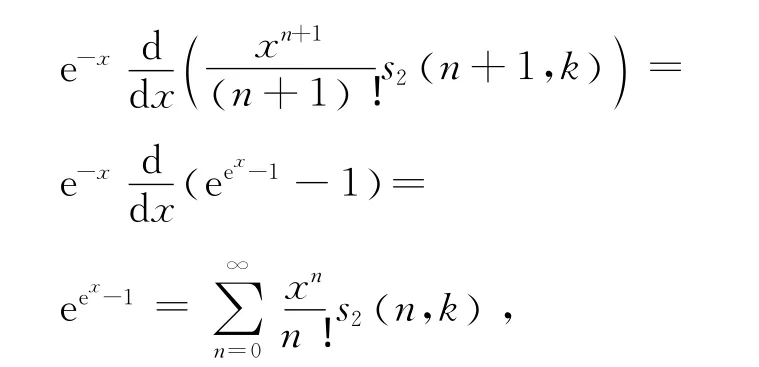
比较等式两边xn的系数，得

例3 在式（6）中令，f（k）＝kr，则

当r＝0时，有

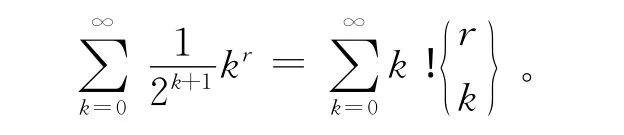
在式（9）、（11）中令f（k）＝kr，则

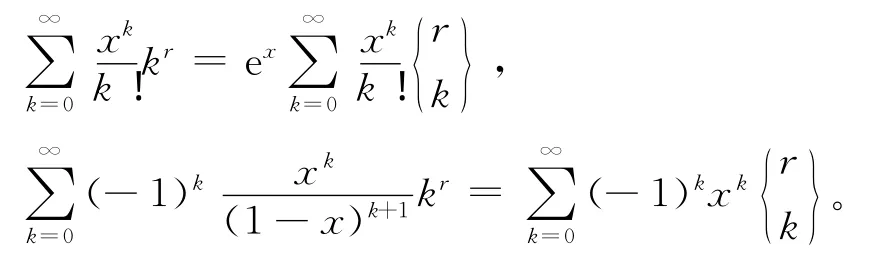
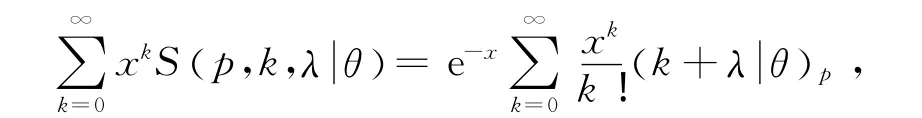
3 结语

本文主要将算子与形式幂级数结合起来，得到了级数转化公式（3）和（4），从第3部分可以看到，（3）和（4）在研究特殊多项式性质方面应用广泛。

［1］Rota G C，Kahaner D，Odlyzko A.On the foundations of combinatorial theory：VIII.finite operator calculus［J］.Mathematical A-nalysis and Applications，1973，142：684-760.

［2］He T X，Hsu L C，Shiue P J S.A symbolic operator approach to several summation formulas for power series［J］.Computational and Applied Mathematics，2005，177：17-33.

［3］He T X，Hsu L C，Shiue P J S.Convergence of the summation formulas constructed by using a symbolic operator approach［J］.Computers and Mathematics with Applications，2006，51（3-4）：441-450.

［4］He T X，Hsu L C，Shiue P J S.Symbolization of generating functions，an application of the Mullin–Rota theory of binomial enumeration［J］.Computers and Mathematics with Applications，2007，（5）：664-678.

［5］He T X，Hsu L C，Shiue P J S.A symbolic operator approach to several summation formulas for power series II［J］.Discrete Mathematics，2008，308：3427-3440.

［6］Knopf P M.The operator（x/d/dx）n and its applications to series［J］.Mathematics Magazine，2003，76（5）：364-371.

［7］Comtet L.Advanced Combinatorics［M］.Dordrecht：Springer，1974：204-212.

［8］Hsu L C，Shiue P J.On certain summation problem and generalization of Eulerian polynomials and numbers［J］.Discrete Mathematics，1999，204（1-3）：237-247.

［9］Boyadzhiev K N.A series transformation formula and related polynomials［J］.International Journal of Mathematics and Mathematical Science，2005，23：3849-3866.