基于规划算法的多层地基一维固结超孔隙水压力估算*

刘红军，上官士青，王 虎

（中国海洋大学1.环境科学与工程学院；2.海洋环境与生态教育部重点实验室，山东 青岛 266100）

太沙基于1923年提出了至今仍在工程界广泛采用的饱和黏土一维固结方程，并用分离变量法给出了解析解。天然地基的成层性使得太沙基一维固结理论不能直接应用，Schiffman等［1］求得了荷载随时间呈线性增长情况下多层地基固结的解析解；Gibson等［2］对大变形固结进行了一系列研究，提出了有限差分求解的孔隙比为控制变量的一维大变形固结方程；谢康和等［3］获得了多层地基在任意变荷载下的解析解；吴雄志等［4］考虑了渗流力的影响，对太沙基一维固结理论进行了修正；Chen等［5］采用了DQM算法提出了多层地基在部分透水界面下且在任意荷载下的解；潘旦光等［6］提出了一种基于直接模态摄动算法的适用于变参数土层的半解析解；吴健等［7］在Gibson地基中压缩指数和渗透指数不同比值条件下，进行了解析解推导和有限元数值分析；Kim等［8］在一维固结理论中引用了接触面边界关系以适应大应变的计算；Huang等［9］分析提出了一种耦合压缩量和超孔隙水压力以及非耦合单纯计算超孔隙水压力的有限元解法；谢新宇等［10］通过电阻网络对太沙基一维固结解进行了模拟。

有限差分在计算固结问题上简便实用，对于时间本身就是离散的；同样采用有限元方法严格的计算固结问题，仍需要对时间进行离散。曾攀等［11］给出了弹塑性多孔介质的参变量变分原理（增量形式），可以得到x，z，t均离散的势能方程，用于构建有限元模型。张洪武等［12］采用二次规划（数学规划的一种）的算法求解了弹塑性biot固结，给出了时间卷积全量形式的参变量变分原理，通过时间卷积不需要迭代。无论通过何种方法考虑时间离散问题都较为复杂，因此笔者尝试不考虑时间离散，建立一种不同固结度下超孔隙水压力分布估算方法，这种情况下模型计算更为简便。

本文基于弹性地基及孔隙比与有效应力线性关系的假设，以分层土总势能公式作为规划算法求解的目标函数，并将固结离散为n个部分进行，通过离散的太沙基解析式描述每个部分的固结过程中时间与超孔隙水压力的对数关系，建立了数学规划模型。该模型可依据平均固结度（以孔压定义，下同）求解多层地基各单元超孔隙水压力分布。该方法计算时不需要按时步进行计算，模型求解简单，无需考虑矩阵运算等求解中的数学问题。

1 计算思路及固结过程的离散

非线性规划是具有非线性约束条件或目标函数的数学规划，是运筹学的1个重要分支，广泛用于经济学中生产力分配、车辆调度、概率论、图论、拓扑学等的计算分析。非线性规划研究1个n元实函数在一组等式或不等式的约束条件下的极值问题，即为1个在可行域中求极值的问题。被求极值的函数称为目标函数，形成可行域的关系式称为约束条件。在太沙基解的经典假设中，地基土被假设为弹性，将地基土离散为n个单元后可以将其视为n个线性弹簧，这些线性弹簧 （代表骨架）的行为特征符合渗流约束下的最小势能原理。对于固结问题可尝试利用规划算法对固结过程中的要素进行分配使整个系统势能最小进行求解。

本文数学模型的计算流程见图1，首先将固结过程离散，分为n部分进行，用太沙基解析解分别表示离散后超孔隙水压力消散的区域，将这种情况下太沙基解析解中无实际物理意义的渗透系数k定义为渗流能力ki。在渗流能力ki总量为一定值的情况下，分配ki的大小使系统势能最小，求得在不同固结度情况下，各土层单元的超孔隙水压力分布。

图1 数学规划算法流程Fig.1 Flow chart for mathematical optimization algorithm

2 基于最小势能原理的控制方程

假设地基为成层弹性体，在均布荷载作用下压缩，其系统总体势能可表示为

式中：∏为土体总势能；F为均布外力；Ei为第i单元的弹性模量（压缩模量）；si为第i层土体的压缩量；s总为地表沉降，即所有分层土体压缩量之和。

基于有效应力原理，假设水体无法压缩（水没有弹性势能），可以得到土体单元有效应力与该单元超孔隙水压力的关系：

式中：d为某单元有效应力增量；du为某单元超空隙水压力增量。

侧限条件下孔隙比的变化增量与竖向有效应力变化增量的关系：

式中：e为孔隙比，a为压缩系数。

某一单元土层压缩量与孔隙比的关系为

代入离散的势能方程可得：

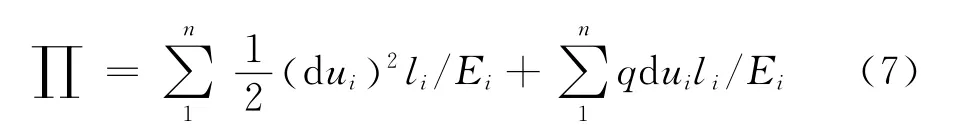
式中：li为第i单元厚度；q为均布荷载（方向为负）。

由势能方程的表述可见，土层总体的势能主要由超孔隙水压力增量du控制，但实际上式（7）仅是“完整的”弹性骨架的全量形式，与水相关的项目由于不能时间离散，不能完整表述，因此略去。模型主要通过解析解的孔隙水压力时间关系约束弹性骨架的变形。Ei在势能方程中可以看做1种权重项，由于本文拟采用的约束条件为太沙基解析解的一种离散，其中已经包含了Ei的影响，因此式（7）中的继续使用Ei作为1种权重将重复考虑弹性模量的影响，应降低Ei对控制方程的权重。在此引入模量影响参数Ai来代替Ei的倒数，用于对势能方程的修正。为了降低压缩模量Ei对控制方程的影响，Ai应是大小变化不大且受Ei影响的参数。

经大量试算，Ai可取Ei的调和平均数，用于协调各单元势能的比例。即

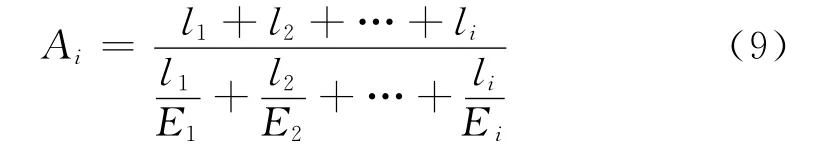
3 基于解析解的时间约束

已知离散后的单层均匀地基固结排水太沙基解析解为式（2）。在本模型中，为便于计算，仅取式中第一项参与计算，同时为了统一时间因数为0时固结度为0，将8/π2也略去，则式其简化为

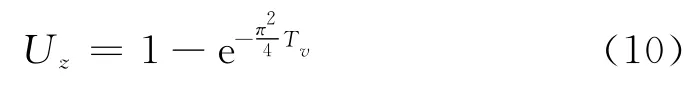
式中：Tv为时间因数。由于本文着重于超孔隙水压力分布的计算，经上述简化后，时间因数与固结度的关系已不准确，但各单元的时间因数比例是统一的，可以用于计算某一固结度下的超孔隙水压力分布。建议采用太沙基解析解的前三项作为约束，以提高计算精度，特别是对于固结度小的单元如果采用式（11）计算误差较大。对于各单元可表述为

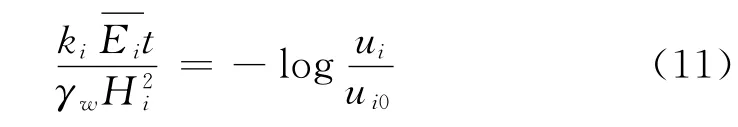
或采用式（2）前三项提高计算精度，表述为

由于式（11）、（12）等时间约束是用于限定各单元渗流能力ki之间的比例关系（见式13），公式中ki前的常数均可省略，即式（2）中ki前的常数π2/4可以省略。式（12）中常数项0.868是为了统一时间因数为0时固结度为0，对原解析解中的8/π2进行的补偿。

根据上述离散方法，每部分固结均消耗一定的渗透能力ki，令这些ki之和为一定值k总可作为一项约束。本模型中可令k总为任意常数C，常数C的大小仅影响时间t与固结度的关系，对于本文所关注的某固结度下各单元超孔隙水压力分布比例不会产生影响。C一般取值为1～5，且随单元数量变化。根据大量试算，k总为分组单元数量、各土层渗透系数的函数，求得k总的函数表达式可使本模型准确计算地基中各单元的固结曲线，有待进一步研究。

式中：为第i部分固结单元的加权调和平均渗透系数。

当地基为单一均质土层时，上式可简化为

对于双面排水的情况，可通过多次试算的方法确定土层中孔隙水压力的的最高点，以该点作为界面将1个双面排水的问题分割为2个单面排水进行计算。或采用简单的0～1选择约束来处理。可设ci为自上而下的渗透能力；为自上而下渗透的调和平均渗透系数；为第i土层单元向下渗流的渗流路径长；为第i单元至第n单元的加权算数平均压缩模量。将某一单元向2个方向渗流所消耗的渗流能力联立在一起，按式（15）进行计算，模型在求解系统势能的最小值时将对渗流方向进行选择，给出各单元变量j的值：

对于1个健康的模型，第i单元发生向上渗流时ci应为0，向下渗流时ki应为0。该规律与j的取值无关，j仅用于保证算法选择的正确性，一般情况下可以将j省略，得式（16）。采用式（16）的计算结果中，对于任何单元的ci或ki必有1个等于0，符合实际情况：

4 模型求解

通过上述讨论，将多层地基的一维固结问题转化为1个求极值的数学规划模型：

该模型是1个在可行域内求极值的纯数学问题，可采用MATLAB优化工具箱（Optimization toolbox）或其他通用数学软件求解。根据式（15），ui和dui可以表述为ki的函数，模型中未知数仅有ki，计算时调整t的大小可获得不同固结度下的超孔隙水压力分布。

5 算例

5.1 算例1

文献［13］对层状土体孔隙水压力的空间变化规律进行了研究，计算了渗透系数不同情况下孔隙水压力的分布趋势，笔者采用本文模型进行了相同的计算，结果如图2所示。该例仅假设上层土体与下层土体渗透系数（k1与k2）的差异，两层土体的弹性模量相同。时间、具体渗透系数的大小、弹性模量的大小并不影响孔隙水压力分布情况。由图2可见，仅渗透系数变化时，模型计算结果与引证文献基本一致。

5.2 算例2

图2 算例1相同固结度下超孔隙水压力沿深度分布曲线Fig.2 Excess pore pressure distribution curve of example 1at same degree of consolidation

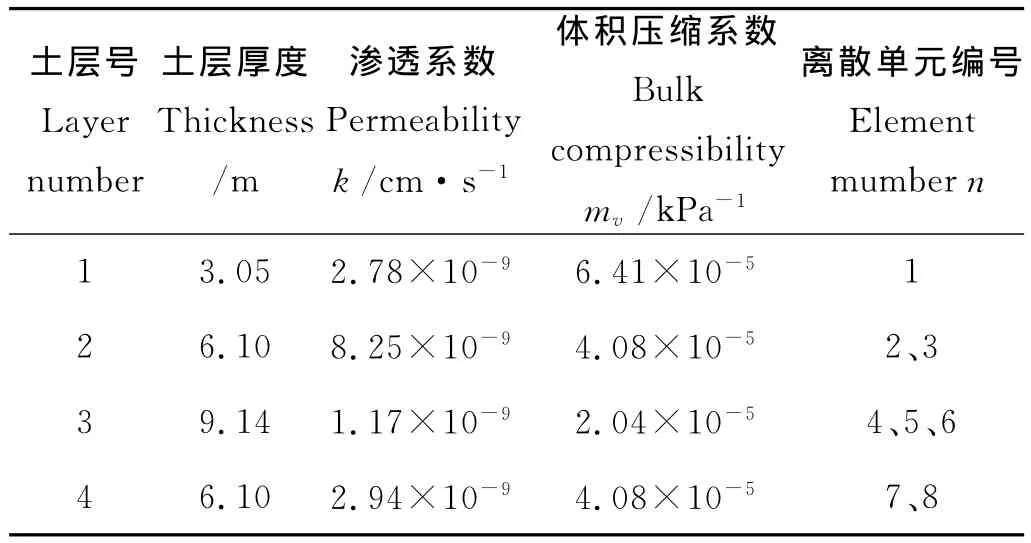
表1 算例2地基参数表Table 1 Layered soil parameters of example 2

5.3 算例3

采用文献［14］中的算例探讨本文算法在压缩模量变化较大的地基中的精度问题。该地基为双层，各土层厚度及力学性质见表2，分为2种情况计算。情况1为土层1覆在土层2上；情况2为土层2覆在土层1上。2种情况均为单面透水，均布荷载，每层土体离散为10个单元参与计算。计算结果如图4，5所示。

本文算法由于采用了基于离散太沙基一维固结解析解的约束，计算结果主要受到固结系数Cv控制。在本例中Cv为一恒定值，如不采用Ai进行修正，超孔隙水压力分布的计算结果应等同于单层均质地基的太沙基解，即类似于函数sin（πz/2H），体现不出双层地基中k和mv的变化。通过Ai修正后，本文模型的解基本符合文献［14］中解的变化规律，说明本文中Ai的修正是有效的。

图3 算例2相同固结度下超孔隙水压力延深度分布曲线Fig.3 Excess pore pressure distribution curve of example 2at same degree of consolidation

表2 算例3地基参数表Table 2 Layered soil parameters of example 3

图4 算例3情况1某固结度下超孔隙水压力延深度分布Fig.4 Excess pore pressure distribution curve of example 2case 1at same degree of consolidation

图5 算例3情况2相同固结度下超孔隙水压力延深度分布Fig.5 Excess pore pressure distribution curve of example 2case 2at same degree of consolidation

在计算情况1的结果中出现了下部单元超孔隙水压力小于上部单元的情况（压缩模量突变处），与实际情况不符，建议在模型中加入一项姿态约束dui＋1≥dui，使计算结果更符合实际情况。在情况1中本文算法与文献［14］的差分解误差较大，约为15%，表现为孔隙水压力线性增长的分界点前移了近一个单元。将情况1下的地基离散的单元数量增加到20后，解的精度有所提高，但孔隙水压力线性增长的分界点与10单元的计算结果变化不大。如果对计算精度要求较高，本文方法不适用于压缩模量变化剧烈的地基。

6 结论

（1）以最小势能原理作为目标函数，太沙基解析式的一维离散作为约束的数学规划模型用于计算多层地基一维固结中某一固结度下超孔隙水压力分布是可行有效的，且不需按时步计算。其计算结果主要受土层固结系数Cv影响，并通过目标函数中的参数A修正，修正后计算结果与差分算法计算结果基本吻合。

（2）规划算法在计算中对压缩模量进行了算术平均处理，如果对计算要求精度较高，该方法不适用于各土层压缩模量变化剧烈的地基。

（3）根据大量试算，新定义的渗流能力的总和k总为分组单元数量、各土层渗透系数等参数的函数，准确确定k总的表达式可使该模型计算固结度于时间的关系，有待进一步研究。

［1］Schiffman R L，Stein J R.One-dimensional consolidation of layered systems［J］.J Soil Mech and Found，1970，964：1499-1504.

［2］Gibson R E，Schiffman R L，Cargill K W.Theory of one-dimensional consolidation of saturated clays.Finite non-linear consolidation of thick homogeneous layers［J］.Canadian Geotechnical Journal，1981，18（2）：280-293.

［3］谢康和，潘秋元.变荷载下任意层地基一维固结理论［J］.岩土工程学报，1995，17（5）：80-85.

［4］吴雄志.考虑渗流力时对太沙基一维固结理论的修正［J］.岩土力学，2004，25（8）：1279-1282.

［5］Chen R P，Zhou W H，Wang H Z，et al.One-dimensional nonlinear consolidation of multi-layered soil by differential quadrature method［J］.Computers and Geotechnics，2005，32（5）：358-369.

［6］潘旦光，楼梦麟.变参数土层一维固结的半解析解［J］.工程力学，2009，26（1）：58-63.

［7］吴健，谢新字，朱向荣.饱和土体一维复杂非线性固结特性研究［J］.岩土力学，2010，31（1）：81-86.

［8］Kim H J，Jose L M.Numerical analysis of one-dimensional consolidation in layered clay using interface boundary relations in terms of infinitesimal strain［J］.International Journal of Geomechanics，2011，11（1）：72-77.

［9］Huang J，Griffiths D V.One-dimensional consolidation theories for layered soil and coupled and uncoupled solutions by the finite-element method［J］.Geotechnique，2010，60（9）：709-713.

［10］谢新宇，王龙，刘开富.饱和土一维固结的电阻网络模拟［J］.岩土力学，2011，32（11）：3455-3460.

［11］曾攀，钱令希.岩土中弹塑性渗透固结问题的参变量变分原理［J］.力学学报，1991，23（4）：484-490.

［12］张洪武，钟万勰.土体固结弹塑性分析的参数二次规划理论及有限元解［J］.岩土力学，1995，16（1）：35-45.

［13］栾茂田，钱令希.层状饱和土体一维固结分析［J］.岩土力学，1992，13（4）：45-56.

［14］Pyrah I C.One-dimensional consolidation of layered soils ［J］.Geotechnique，1996，46（3）：555-560.