振动信号离散余弦变换域维纳滤波算法

张 峰，马舒啸，石现峰

（西安工业大学，陕西 西安710032）

0 引言

信号采集在自然条件下都不可避免地会混入噪声，从而造成后期信号处理时的失真，可以看出滤波技术在数字信号处理中有着极其重要的地位。例如，汽轮机运行状况的实时监测一般是通过对其振动信号进行采集和分析来完成的，由于现场复杂工作环境的影响，采集到的振动信号中往往含有大量噪声，要获得振动信号的准确特征，并依据这些特征进行状态监测和故障诊断，必须首先进行信号的滤波处理。又如，在非接触式引信中，由于是依靠物体反射信号来完成起爆任务，所以是否可以排除噪声干扰从而获得纯净信号，是判断引信工作质量的重要指标［1－2］。

本文以汽轮机振动信号为主要对象，研究广泛振动信号的去噪处理。

振动信号是机械领域内常见信号，由于其在后期处理中高相位敏感性以及高滤波效果的要求，所以本文采用汽轮机振动信号为研究对象［3－4］。

本文针对上述的问题，提出了振动信号离散余弦变换域维纳滤波算法。

1 振动信号及滤波要求

1.1 振动信号的采集

为便于算法分析研究更具有针对性，进行了实际工业现场汽轮机振动信号的现场实测采集。信号采集所用的振动传感器为美国Bentley公司的电涡流式传感器，汽轮机转轴理想转动频率为50Hz（即3 000r／min），按照32倍频采样频率（即fs＝50×32＝1 600Hz）进行信号采样，采样点数为128点。较为理想情况下采集得到的振动信号如图1所示。为验证算法的去噪性能，对采集得到的振动信号加入随机噪声，加噪后的振动信号如图2所示。

图1 实测汽轮机振动信号Fig.1 The measured steam turbine vibrationsignals

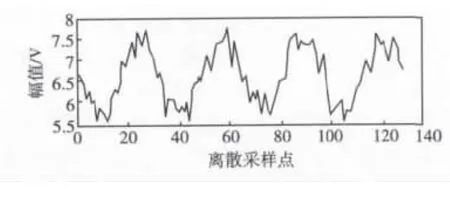
图2 加噪后汽轮机振动信号Fig.2 Steam turbine vibration signals with noise

1.2 振动信号的滤波要求

噪声的存在会影响对汽轮机工作状态特性信息的准确获取，在后续的谱估计、特征提取等分析之前，必须进行去噪声处理。对汽轮机振动信号的噪声处理一般需满足如下两点基本的要求：

1）汽轮机的运行特征信息都与振动信号的相位有关，因此首先需要保证信号滤波后不产生或者较少产生相位失真，但是滤波算法相频特性的非线性会引起波形的畸变，这种畸变正是相位失真的一种表现。所以，这就要求滤波算法具有较好的线性相位特性。

2）在保证线性相位前提下，能够有效滤除噪声，获取最真实的代表汽轮机运行状况的振动信号。尤其在后续振动信号的谱估计中，噪声对谱估计算法的方差性能以及谱估计的准确程度会有非常大的影响，需要尽可能地去除掉噪声的干扰。

2 基于DCT的信号滤波算法及其存在的问题

2.1 基于DCT的去噪算法

离散余弦 变 换 （Discrete Cosine Transform ，DCT）是一种实数域的正交变换，对长度为N的有限长实序列x（n），其离散余弦变换用Xc（k）表示，定义为：

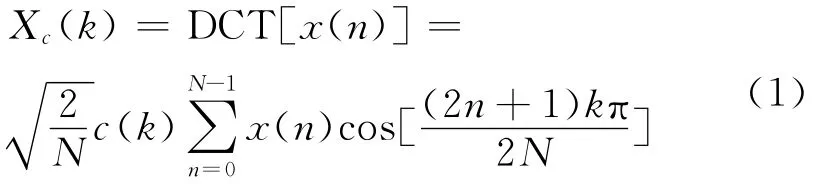
其中：

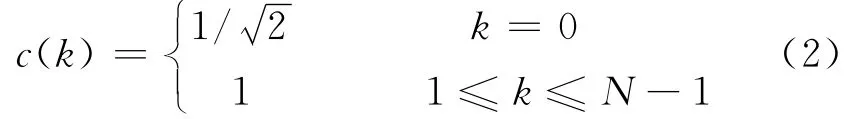
反变换为：

相比较于傅里叶变换、哈尔变换等其他正交变换，离散余弦变换具有高度解相关性，变换以后的数据相关性降低，且能量集中［5－7］。也就是说，信号通过DCT变换以后，变换结果序列的相关性降低，且主要能量集中在前面的一些系数上。这些特性是DCT应用于信号压缩及去噪的基本依据。利用DCT进行信号去噪的一般算法过程为：先将输入数据按式（1）进行DCT变换；将变换后的数据根据能量集中的效率保留前面的数据，抛弃后面的数据；然后把保留的数据补0到原始数据长度；再按式（3）进行DCT逆变换，就获得了滤波后的数据。

2.2 算法用于振动信号滤波存在的问题

由上述基于DCT的信号去噪的算法原理可以看出，直接利用DCT进行信号滤波是一种非线性的滤波方法，且滤波效果取决于所保留的DCT变换系数的个数［8］。利用上述算法对图2所示加噪后的振动信号滤波效果同原始信号进行对比后的结果，如图3所示。

由图3（a）可看出，当保留的系数较少时，能够在较大程度上滤除高频噪声的干扰，但滤波后信号的相位失真明显。由图3（b）可看出，当保留的系数较多时，相位失真虽然较小，但滤波效果较差，很多噪声干扰无法得到有效去除。产生这一问题的原因是，DCT算法不是线性滤波，因而无法保证线性相位，所以会引起波形的严重畸变。可见，离散余弦变换应用于汽轮机振动信号的滤波虽然能够起到一定的去除噪声的作用，但也存在着滤波效果和线性相位之间的矛盾，需加以改进以适应于汽轮机振动信号的滤波处理。

图3 利用DCT去噪后的汽轮机振动信号Fig.3 After using DCT denoising of steam turbine vibration signals

3 DCT域维纳滤波算法原理

3.1 维纳滤波［9］

维纳滤波是基于最小均方误差的线性滤波器，可以设计成有限冲激响应（FIR）的也可以设计成无限冲激响应（IIR）的。以FIR维纳滤波为例，其基本原理如图4所示。

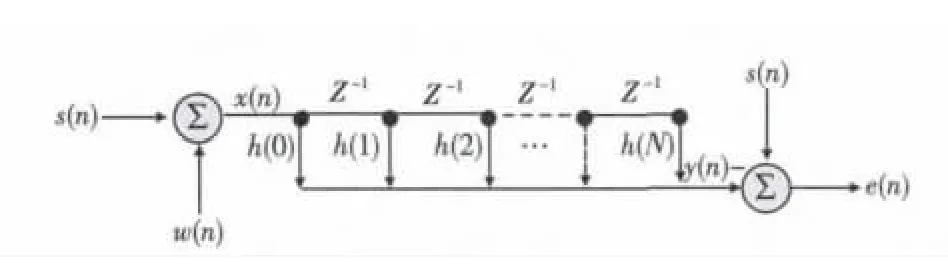
图4 维纳滤波算法原理图Fig.4 The principle diagram of the wiener filter algorithm

图中，s（n）为理想信号，在理想无噪声的环境中原始汽轮机振动信号是正弦信号；ω（n）为噪声；x（n）为观测信号；h（n）为维纳滤波器系数；y（n）为维纳滤波输出信号；e（n）为处理误差。由图4可得到：

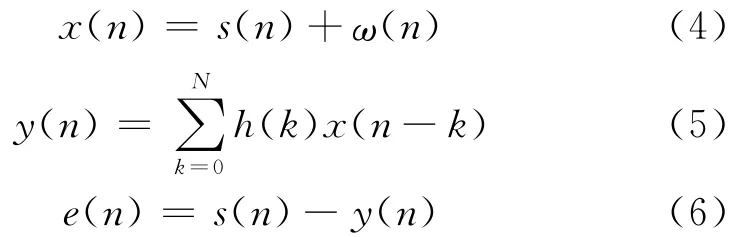
则滤波算法的均方误差为：

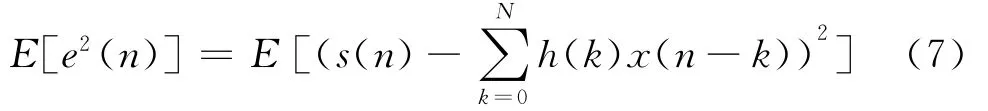
维纳滤波器系数h（n）确立的原则是使滤波输出的均方误差，即公式（7）中E［e2（n）］取得最小值。满足这一条件的滤波器系数h（n）可由Wiener－hopf方程求解，即：

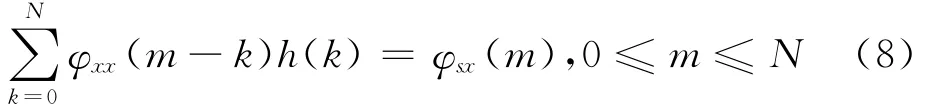
公式（8）中，φxx（m）为观测信号的自相关序列，N为维纳滤波器的阶次，φsx（m）为理想信号与观测信号的互相关序列。

3.2 维纳滤波与DCT的结合应用

维纳滤波是一种线性滤波，只要系数设计合理，对线性相位会有较好的保证，但要获得最小均方误差特性，则要求信号是平稳随机信号。对采集到的汽轮机振动信号进行时域维纳滤波的仿真结果如图5所示。

图5 时域维纳滤波效果图Fig.5 The effect of The time domain wiener filtering

从图5可以看出，由于振动信号从本质上讲是非平稳的，且信号采集长度越长，非平稳性越明显，如果直接在时域进行维纳滤波，虽能保证线性相位，但会难以取得较好的噪声滤除效果［10］。

考虑到DCT变换具有高度解相关性，且能将信号的主要能量进行集中，则可以考虑在振动信号的DCT域进行维纳滤波，将两者有机结合起来，更好地发挥维纳滤波的作用。维纳滤波与DCT变换结合进行振动信号去噪的算法过程如下：

1）按公式（1）分别对观测信号和理想信号进行离散余弦变换；

2）选定阶次N，在DCT域按式（8）建立起Wiener－hopf方程；

3）求解 Wiener－hopf方程，得到维纳滤波系数h（n）；

4）利用h（n）对观测信号的离散余弦变换的前N个系数进行维纳滤波处理，同时将后面的DCT系数置为0；

5）将步骤4）处理后的结果补零恢复为原始长度，再按式（3）进行离散余弦反变换，得到滤波处理后的汽轮机振动信号。

4 DCT域维纳滤波效果分析

4.1 仿真结果

上述算法基于Matlab进行了仿真实现，对图2所示加噪的振动信号进行去噪处理，得到的结果如图6所示。

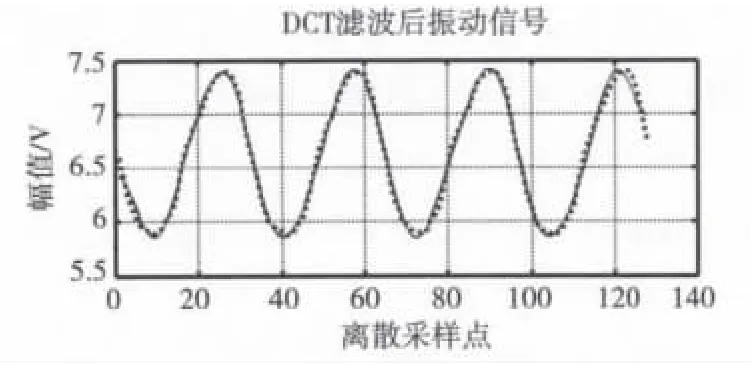
图6 振动信号DCT域维纳滤波结果Fig.6 The results of Vibration signal with DCT domain wiener filtering

4.2 结果理论分析

从算法的理论研究上看，由于DCT本身是非线性的，也具有无法同时满足良好滤波要求和良好线性相位的要求。所以我们将DCT和维纳滤波相结合，这样从算法的原理上，我们首先运用维纳滤波的线性滤波特性保证振动信号在去噪效果和线性相位上都取得良好的结果，另外运用DCT的能量集中原理去降低振动信号维纳滤波的阶次。这样一来便可很好地解决前言中所提及的问题。

从算法的原理也可以看到，当信号长度较长时，也会造成DCT算法的能量集中程度降低。

从图6可看出，在DCT域所进行的维纳滤波算法取得了较好的噪声滤除效果，最大程度地进行了噪声与信号的分离。再对比图6和图1，可看出，由于在算法中，噪声滤除主要还是由维纳滤波实现的，因此该算法能够保证滤波器的线性相位特性，滤波后信号没有明显的相位失真。实践表明，本文所提出的振动信号离散余弦变换域维纳滤波算法能够满足该类振动信号的滤波需求。

5 结论

本文提出了振动信号离散余弦变换域维纳滤波算法。该方法将DCT的能量集中特性和维纳滤波的线性滤波特性相结合从而更好地发挥维纳滤波的作用。仿真表明在对汽轮机振动信号的去噪处理中取得了较为理想的效果。该算法的优缺点如下：

1）DCT域维纳滤波去噪算法有较好的相位特性，用于振动信号的滤波处理能够保证滤波后信号不产生明显的相位失真。

2）在保证相位特性的同时，算法能够取得较好的滤波效果，性能优于单独使用DCT滤波算法和维纳滤波算法。

3）由于DCT的能量集中特点，算法中维纳滤波的阶次较低，运算复杂度小，同时还可以实现对振动信号数据量的压缩处理。

4）当信号采集长度较长时，信号DCT域能量集中程度降低，会影响算法的滤波效果。注意到振动信号一般来讲具有循环平稳的特点，且算法没有明显波形畸变失真，这时可以通过分段处理的方式解决这一问题。

［1］单剑锋，崔占忠，司怀吉.小波变换去噪方法在无线电引信信号处理中的应用的研究［J］.北京理工大学学报，2005，25（3）：256－257.

［2］李月琴，栗苹，闫晓鹏，等.小波变换模极大去噪法在无线电引信信号处理中的应用［J］.兵工学报，2008，29（10）：1172－1173.

［3］张军，王金平，朱波.旋转机械振动信号处理中的滤波及特征提取技术［J］.南京工程学院学报（自然科学版），2009，7（03）：15－17.

［4］王金平，邓艾东，丁轲轲.基于DSP的汽轮机振动信号采集系统的研究与设计［J］.电站系统工程，2008，5：49.

［5］管博，胡劲松.基于DCT的旋转机械振动信号压缩方法研究［J］.风机技术，2007：80－81.

［6］管博，胡劲松.基于DCT的旋转机械振动信号无相移滤波方法研究［J］.汽轮机技术，2007，49（04）：285－287.

［7］陈佳元，张秋菊.基于DCT的压缩机振动信号压缩方法研究［J］.压缩机技术，2009：5－7.

［8］陈章龙等.基于DCT的微弱信号提取和识别［J］.噪声与振动控制，2012，32（01）：105－107.

［9］Wu Qingju，Tian Xiaobo.Receiver Function Estimated by Wiener Filtering［J］.Earthquake Research in China，2003，17：387－388.

［10］Li Qian，Zhao Jiyin，Yang Yusen，et al.Image De－noising Algorithm Based on Correlation Model with Wiener Filter in Wavelet Domain［C］∥ 3rd International Symposium on Instrumentation Science and Technology，2004：110－114.