非高斯随机分布系统研究现状的分析

屈毅QU Yi；穆丽宁MU Li-ning；赖展翅LAI Zhan-chi

（①咸阳职业技术学院电子信息系，咸阳 712000；②兰州理工大学电气工程与信息工程学院，兰州 730050）

（①Department of Electronics and Information，Xianyang Vocational Technical College，Xianyang 712000，China；②College of Electrical and Information Engineering，Lanzhou University of Technology，Lanzhou 730050，China）

0 引言

在近几十年，随机系统是控制领域中的一个重要研究方向。经过多年的发展，随机控制已具有完善的理论体系。目前，随机系统研究的主要成果有自校正控制，线性高斯二次型，马尔可夫参数过程控制，最小方差控制等，其主要研究系统输出均值和方差等满足规定的性能指标[1,2]。

1 非高斯随机分布系统研究背景

在设计随机系统时，假设系统变量服从高斯分布。这样，在粮食加工中的粮食颗粒尺寸的大小分布、锅炉炉腔燃烧的火焰分布等众多工业生产过程中，系统变量如果不符，就需要从新假设高斯分布[3,4,5]。

在上述工业生产中过程中，不难看出系统变量的分布与动态变化过程是紧密相关的，但是这些随机的统计特性不满足高斯分布的假设。依据概率知识，系统中变量分布可由概率密度函数[1,2]（Probability Density Function：PDF），即γ（y，t）来描述。在时刻t，概率密度函数γ（y，t）可由偏微分方程（Partial Differential Equation：PDE）得到。

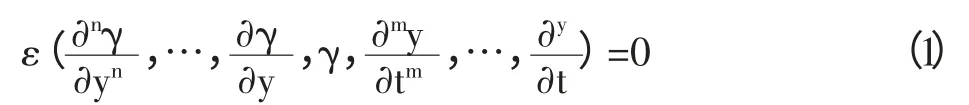
式中ε（·，·）为非线性函数。但是，直接应用该模型十分困难。

2 非高斯随机分布系统建模国内外研究现状

非高斯随机分布系统控制是控制领域界研究的一个热点，也是一个亟需发展的研究领域。经过近十年的发展，非高斯随机分布控制已形成一个较为完善的理论研究框架。

2.1 非高斯随机分布系统的建模理论

2.1.1 非高斯随机分布系统的静态模型

①平方根B 样条模型。建模原理与线性B 样条模型近似，不同的是逼近的是系统输出概率密度函数的平方根。

②有理B 样条模型。利用B 样条基函数与权值向量之间的有理函数关系逼近系统输出概率密度函数。

③有理平方根B 样条模型。建模原理与有理B 样条模型近似，不同的是逼近的是系统输出概率密度函数的平方根。

2.1.2 非高斯随机分布系统的动态权值模型

由于基函数是预先指定的函数，则系统输出概率密度函数γ（y，u（t））的数学表示就可转化为用与基函数相对应的权值来描述（可将这组权值用向V 表示），即动态权值模型的表达式如下[1]：

对于非高斯离散随机分布系统，则动态权值模型的表达式如下[1]：

式中函数f（·，·）表示权值向量与控制输入之间具有线性或者非线性关系。

2.2 非高斯随机分布系统控制国内外研究现状

非高斯的随机分布系统建立后，就需要设计一个控制算法，以此来实现系统输出概率密度函数追踪目标概率密度函数，这样满足期望或者规定的性能指标。

2.2.1 非高斯随机分布系统常用性能指标

①直接型性能指标。非高斯随机分布系统实际输出概率密度函数γ（y，u（t））应逐渐收敛于给定的目标概率密度函数γg（y），我们称为直接型性能指标。

②二次型性能指标。非高斯随机分布系统研究中最常用的性能指标，我们称为二次型性能指标，其表达式如下所示：

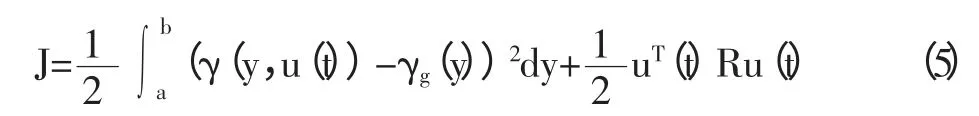
式（5）中第一项是系统输出概率密度函数测量值γ（y，u（t））和目标值γg（y）之间的测度，第二项是对非高斯随机分布系统输入能量的约束。

③平方根二次型性能指标。在平方根二次型性能指标中，系统输出概率密度函数的测量值和目标值之间的测度，我们要用测量值的平方根与目标值的平方根的差值的平方的积分来表示：

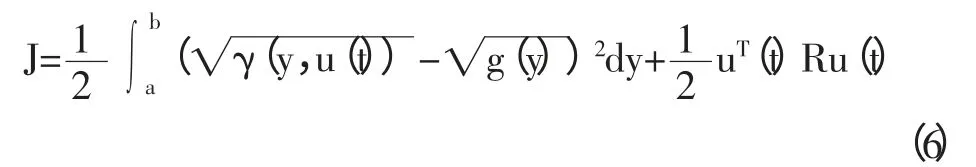
式（6）中第二项是对非高斯随机分布系统输入能量的约束。

2.2.2 非高斯随机分布系统常用控制算法

①系统二次性能指标J 具有非负性，这与李亚普诺夫函数（Lyapunov function）的基本性质一致，故可将二次性能指标J 做为一个李亚普诺夫函数，然后根据李亚普诺夫函数稳定判据，可求得相应的控制器，即根据不等式∂J/∂t≤0 可求得。

②结构化控制算法。以上系统控制器设计时，仅研究系统控制输入和输出量，并未考虑控制器的结构，被便于分析系统的稳定性和鲁棒性。从系统鲁棒性和稳定性的角度出发，在设计系统控制器时，首先有清晰的结构，比如系统输出PDF 广义PID 控制器，该PID 控制器不仅是时间上的函数，也是空间上的函数，与传统的PID 控制不同。

3 总结

非高斯随机分布系统控制是控制理论与应用研究领域的一个非常重要的分支。主要目标就是通过系统特性来设计确定非高斯随机分布系统的稳定性。

[1]屈毅,李战明,李二超.随机分布系统的神经保性能控制器设计[J].计算机集成制造系统,2012(11).

[2]张柏,陈敏泽,周东华.一种非线性非高斯随机系统的故障诊断方法[J].控制工程，2005(S2).

[3]Qu Y,Li Z.M,Li E.C.Fault Tolerant Control for Non-Gaussian Stochastic Distribution Systems [J].Circuits Syst Signal Process,2013,32(1):361-373.

[4]Guo L,Wang H.Observer-Based optimal fault detection and diagnosis using conditional probability distribution [J].IEEE Transactions on Singnal Processing,2006,54(10):3712-3719.

[5]Qu Y,Li Z.M,Li E.C.Fault detection and diagnosis for non-Gaussian stochastic distribution systemss with time delays via RBF neural networks[J].ISA Transactions,2012,51:786-791.

[6]Wang H,P.Afschar,Yue H.ILC-based generalised PI control for output PDF of stochastic systems using LMI and RBF neural networks [J].Proc.of the IEEE Conference on Decision and control,2006:5048-5053.

[7]Qu Y,Li Z.M.,Li E.C.Fault Detection and Diagnosis for Non-Gaussian Singular Stochastic Distribution Systemss via Output PDFs[J].Automatika,2012,53(3):236-243.