快速巧解材料力学静定梁的约束力及剪力弯矩图
2014-11-28张圣光ZHANGShengguang
张圣光ZHANG Sheng-guang
(东北农业大学工程学院农业机械化及其自动化系,哈尔滨 150030)
(Department of Agricultural Mechanization and Automation,Engineering College,Northeast Agricultural University,Harbin 150030,China)
0 引言
计算约束反力是画剪力弯矩图的基础,一旦求错就导致后面的解体都出错,笔者根据自己的解题经验总结出了“四大原理”,避免用理论力学解题时的繁琐,方便快捷。
1 求静定梁约束反力的“四大原理”
1.1 抬水原理

图1 抬水原理图
1.2 翘板原理
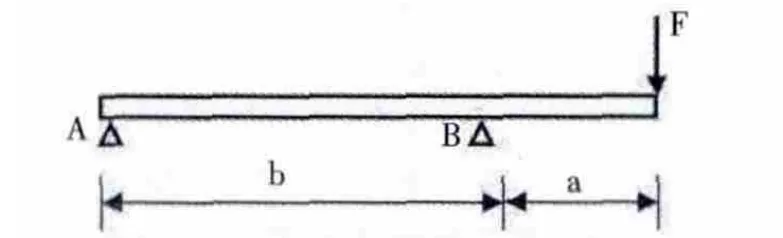
图2 翘板原理图
翘板原理一定要注意力的方向,距离力远端与力的方向相同,距离力近端与力的方向相反。
1.3 力偶原理(↓方向向下)
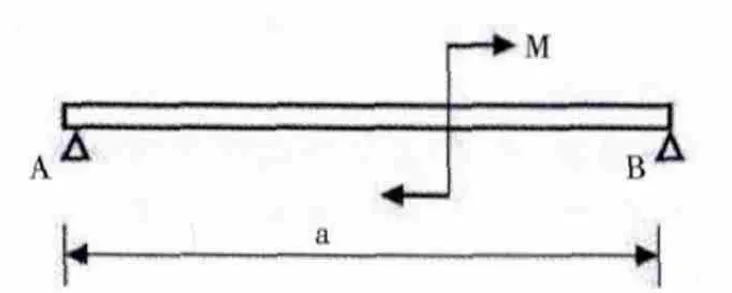
图3 力偶原理图
分母a 为支点AB 的距离。两个支反力的方向相反且支反力构成力偶的方向和已知力偶的方向相反。图3 已知力偶的方向为顺时针,所以支反力构成力偶的方向为顺时针。
1.4 q 原理
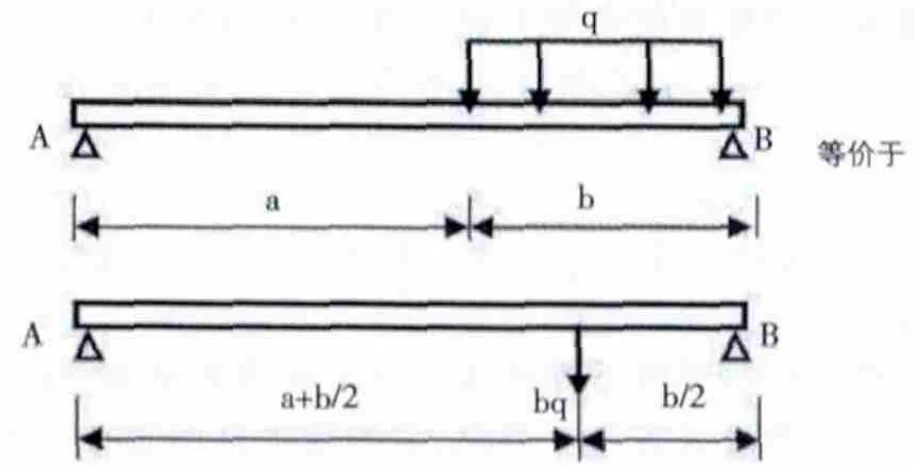
图4 q 原理图
所谓q 原理即均部载荷问题,它综合了前面所讲的抬水原理和翘板原理。
对于既有力,力偶和均布载荷作用的梁要分别求其反力然后叠加求其合力。综上如果静定梁既有力偶,力和均布载荷作用时应分别算出再求其矢量和。
以上是求静定梁约束反力的“四大原理”的总结规律。
2 分析载荷画剪力弯矩图
材料力学的教材基本都是先例出剪力弯矩的平衡方程在画出剪力弯矩图。虽然准确但也比较麻烦,更容易出错。下面我们用新的思维的方法直接画剪力弯矩图。这样无论在工程中的力学分析,还是考试解题都节省了时间。当然,总结规律要依靠高等数学,理论力学为基础。
如图5 所示直梁上作用有任意分布载荷,以梁的左端为坐标原点,取x 轴向右为正,x 处载荷集度为q(x),并规定向上的去(x)为正。在梁中截取微段dx。微段上的分布载荷q(x)视为均匀分布,左截面内力为M(x)和Fs(x),右端截面为M(x)+dFs(x),假设内力为正[1]。
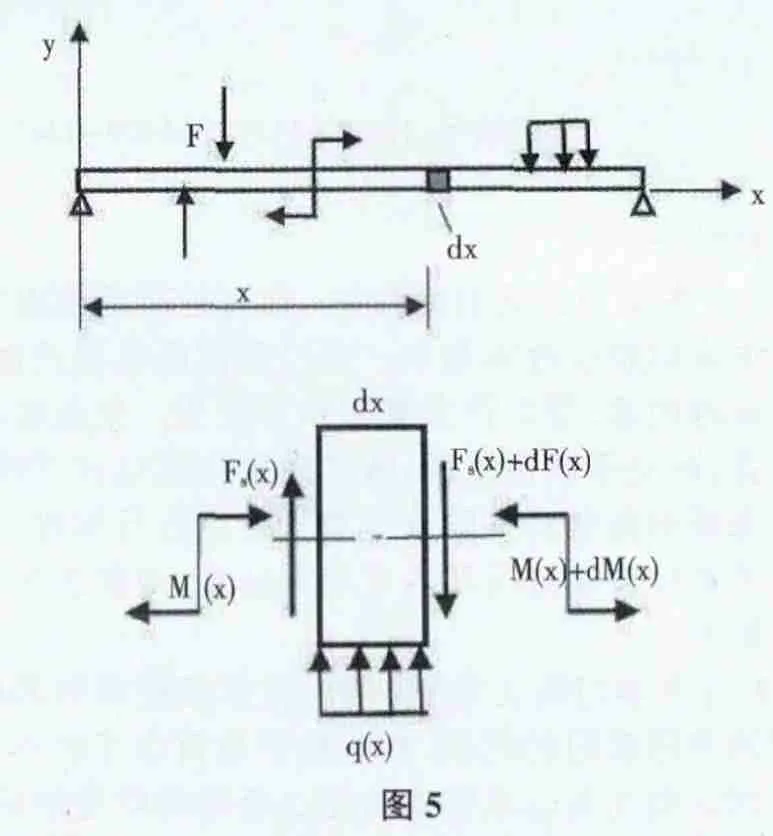
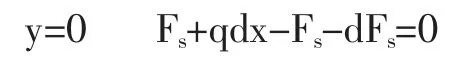

所以经过高等数学和理论力学的推导笔者总结出“三看一算”口诀:①看突变;②看趋势;③看增减;④算大小。
具体解释为对于画剪力图,一看突变如果在梁的某处出现力,则在剪力图上产生突变即力突然变大。二看趋势即看q(x)的趋势,当q(x)为0 时剪力画成平行于x 轴的直线,当q(x)为常数时剪力画成倾斜的直线,当q(x)为斜线时即为一次函数时剪力画成弯曲的曲线。三看增减当q(x)为减函数时F(x)的斜率逐渐减小,F″(x)<0 应画成凸函数,当q(x)为增函数时F(x)的斜率逐渐增大,F″(x)>0 应画成凹函数。在画剪力图时q(x)很少为一次函数一般为常数或0。四算大小,q(x)在某一区间跟x 轴围成的面积即为F(x)的变化量同理,画弯矩图参照剪力图。一看突变如果在梁的某处出现力偶,则在弯矩图上产生突变即弯矩突然变大。二看趋势即看剪力图F(x)的趋势,当F(x)为0 时弯矩画成平行于x 轴的直线,当F(x)为常数时弯矩画成倾斜的直线,当F(x)为斜线时即为一次函数时剪力画成弯曲的曲线,曲线怎么弯曲要看去F(x)的正负及函数的增减性。三看增减,当F(x)为减函数时,M(x)的斜率逐渐减小,M″(x)<0 应画成凸函数,当F(x)为增函数时,M(x)的斜率逐渐增大,M″(x)>0 应画成凹函数。四算大小,F(x)在某一区间跟x 轴围成的面积即为M(x)的变化量。
下面笔者通过一道例题运用求约束力的“四大原理”以及力弯矩图的画法的“三看一算”口诀解静定梁的约束力以及画剪力弯矩图。

qa(↑方向向上);qa(↑方向向上)(根据q 原理分析均部载荷q)
qa(↓方向向下);3qa(↑方向向上)(根据翘板原理分析力2qa)
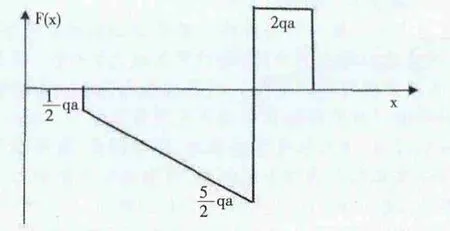
图7 剪力图
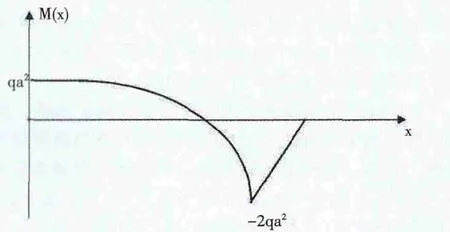
图8 弯矩图
综上所述通过总结求约束力的“四大原理”以及力弯矩图的画法的“三看一算”口诀,清晰明确,直观具体,使材料力学的解题更加简单方便。
[1]赵淑红.材料力学[M].北京:化学工业出版社,2010.
[2]金江.《材料力学》教材改革初探[J].南通工学院学报(社会科学版),1998(04).
[3]王霞,李占君.科学方法论在材料力学课程教学中的应用[J].安阳工学院学报,2010(06).
