非线性超声检测信号提取的电路设计及测试

陆铭慧，王 旭

(无损检测技术教育部重点实验室(南昌航空大学)，南昌 330063)

0 引言

超声非线性是指大振幅声波在介质中传播时发生的如波形畸变、谐波滋生、逾量衰减、声饱和及空化等现象，它随着介质性质的变化而变化。材料中微小缺陷的超声非线性检测，本质上反映的是其对声波非线性的影响。实际上超声波在材料中的传播都是非线性的，只是大多数情况下，小振幅声波非线性效应极其微小，不易观察。而由缺陷所引起的不连续和不均匀在大幅度超声的作用下将表现出很强的非线性效应，可以通过相应的测量方法获得有用的非线性特征，有效地对微缺陷进行无损评价［1-5］。

声波在介质中传播时，会与介质中微观缺陷发生作用，导致波形发生畸变。一列频率为f 的射频信号在传播过程中与微观缺陷相作用，会产生频率为2f、3f 等谐频信号。分析谐频信号的幅值特征，能够判断材料中的微观缺陷大小。但是，相对于基频信号幅值而言，谐频信号幅值通常很小，在测量此类信号幅值时，应采取相应措施来识别谐频信号［6-8］。

1 检测系统搭建及测试

分别采用频率为5、10 MHz 的换能器进行发射和接收，分析基波信号对谐波信号的影响。实验方框图如图1 所示，其中发射及接收换能器均为铌酸锂换能器(声学线性材料)，测试材料为25 mm 厚的熔融石英试样。

给图1 中的待测试件1 个脉冲群发射信号，并注意避免接收器的输出饱和。然后将接收换能器接收到的信号进行傅里叶变换，得到线性显示图谱(图2)。

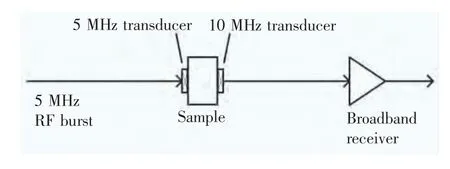
图1 铌酸锂压电换能器以及医用耦合剂进行实验的方框图Fig.1 Block diagram of Lithium niobate piezoelectric transducer and medical coupling agent

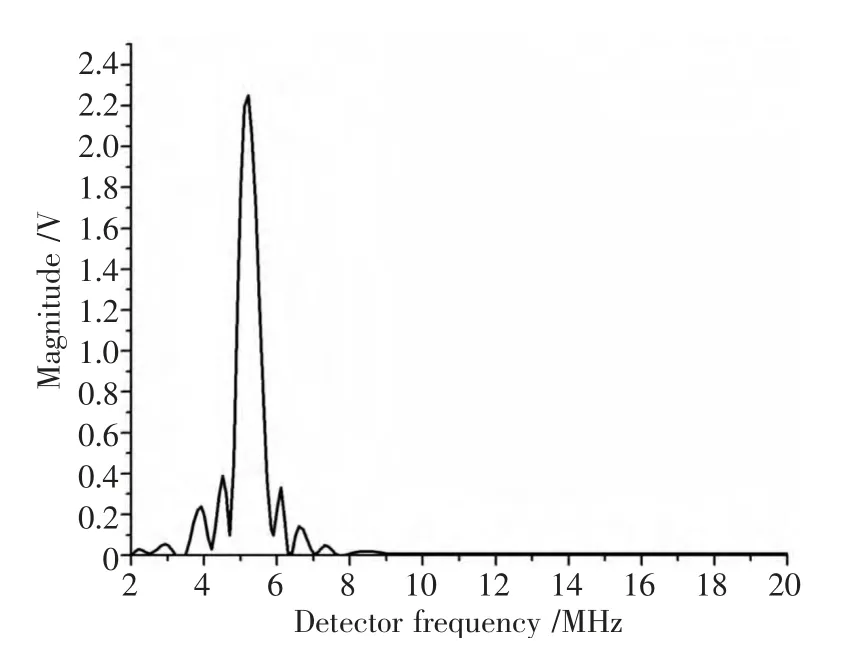
图2 傅立叶变换的线性图谱Fig.2 Linear map of the Fourier transform

从图2 可以看出，信号几乎为纯净的且幅值为2.2 V 的5 MHz 信号，在10 MHz 处的二次谐波信号很小，仅有0.01 V，几乎无法观察到。为解决此问题，可在接收换能器与宽带接收器之间接入一个高通滤波器［9-10］，如图3 所示。

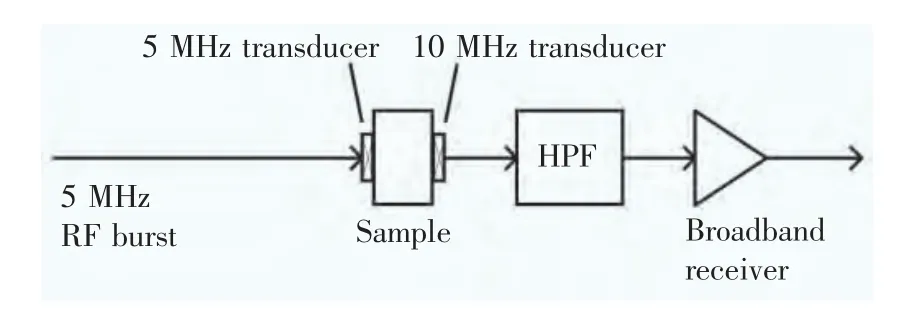
图3 在换能器与接收器之间接入一个高通滤波器Fig.3 A high-pass filter between the transducer and the receiver

为了能更好的观察到二次谐波信号，需要将接收信号中5.5 MHz 以下的低频部分滤除。故设计一个截止频率在5.5 MHz 的四阶有源巴特沃斯高通滤波器用于优化检测系统，滤除不需要的频段信号。通过对接收到的信号做傅立叶变换，可以得到线性坐标幅频图(图4)。

从图4 可以看出，在16 MHz 处出现了比较强的三次谐波信号。产生三次谐波的原因是没有对功率放大器及发射换能器的输出所产生的失真做任何处理。为了更好地观察二次谐频，必须减少来自于发射换能器的三次谐频信号;因此，设计一个截止频率在5.5 MHz 低通滤波器接在发射换能器前，如图5 所示。

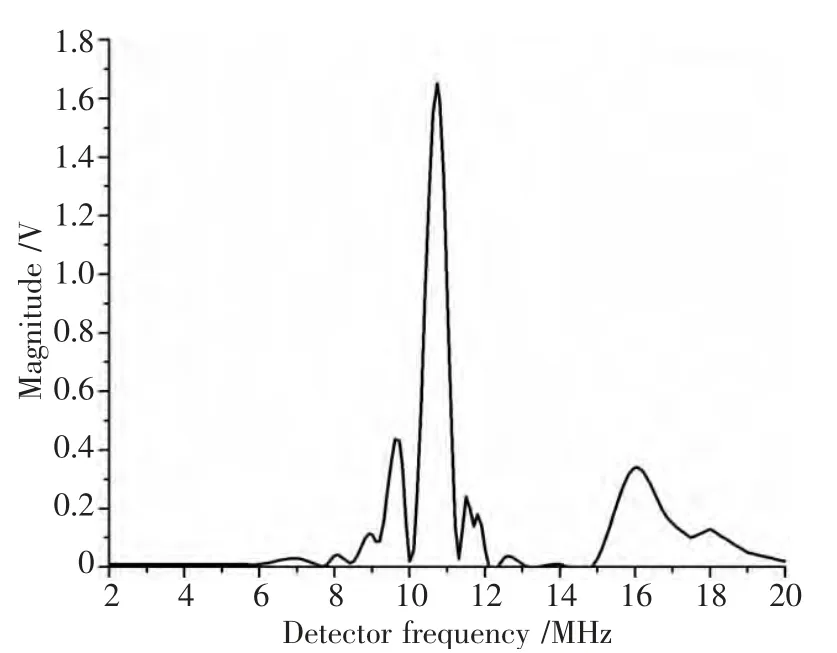
图4 使用HPF 后线性坐标幅频图Fig.4 Linear coordinate amplitude-frequency diagram after using HPF

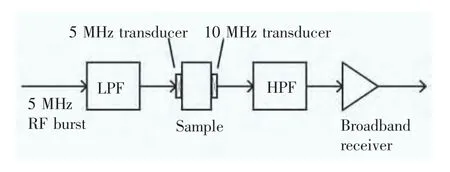
图5 同时使用高、低通滤波器组成的完整滤波系统Fig.5 Integrated filter system composed of high and low pass filter

将接收到的信号进行FFT 变换后可以得到如图6 所示的线性坐标幅频图，信号中5 MHz 处的基波信号由2.2 V 被抑制到0.01 V 以下，而16 MHz 附近的三次谐波信号也被降低至0.01 V 左右，所需观察的10 MHz 处的二次谐波信号为2.1 V。在图6 中可以观察到较为纯净的二次谐波信号，实现了在大振幅信号中提取小振幅信号。

2 滤波系统的研制和仿真效果

根据频率响应特点，滤波器可分为巴特沃思型、切比雪夫型、贝塞尔型及考尔型。其中，巴特沃思型滤波器具有最大平坦幅频响应的特性，且具有良好的线性相位特性，其数学分析和网络结构简单等优点，目前被广泛采用［11］。

巴特沃斯滤波器的特点是通频带内的频率响应曲线最大限度平坦，没有起伏，而在阻频带则逐渐下降为零。巴特沃斯滤波器的振幅对角频率单调下降，并且也是唯一的无论阶数，振幅对角频率曲线都保持同样的形状的滤波器。只不过滤波器阶数越高，在阻频带振幅衰减速度越快。故本研究选用巴特沃斯型滤波电路来设计一个滤波系统用于提取二次谐波信号。

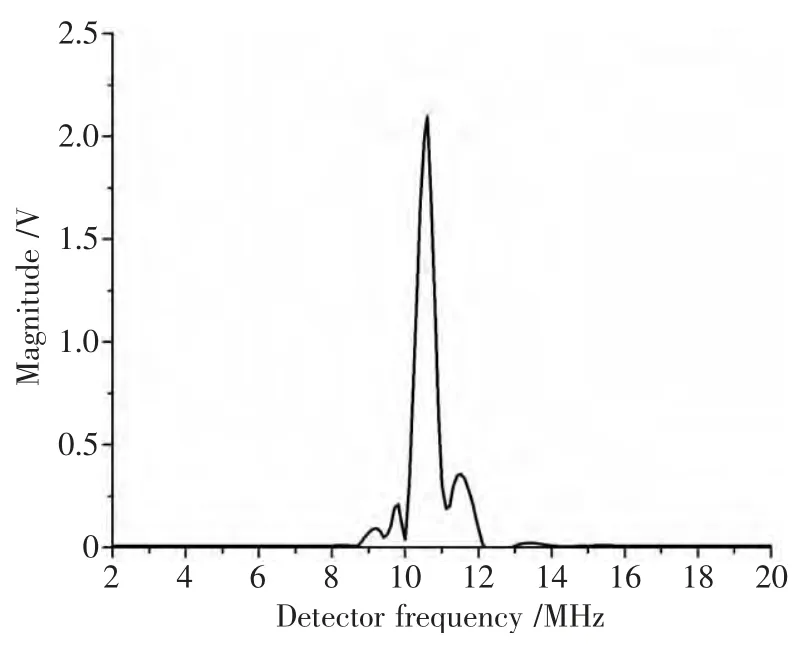
图6 使用HPF 及LPF 后线性坐标幅频图Fig.6 The linear coordinate amplitude-frequency diagram after using HPF and LPF

2.1 四阶低通滤波器的设计

低通滤波器的功能是通过从0 到某一截止角频率ωH的低频信号，而将所有超过截止频率ωH的信号给予衰减，带宽为BW=ωH/2π。

二阶Sallen-Key 低通滤波器如图7 所示。它是由2 节RC 滤波器电路和同向比例运算放大电路组成，其特点是输入阻抗高，输出阻抗低［12］。

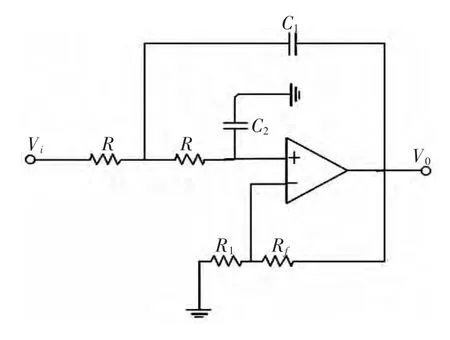
图7 二阶低通滤波器Fig.7 Second-order low-pass filter

取C1=C2=C，根据KCL 求得传递函数为:

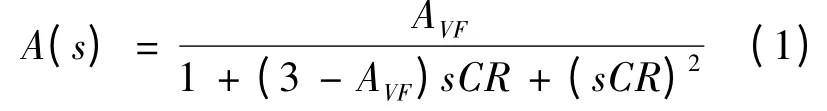
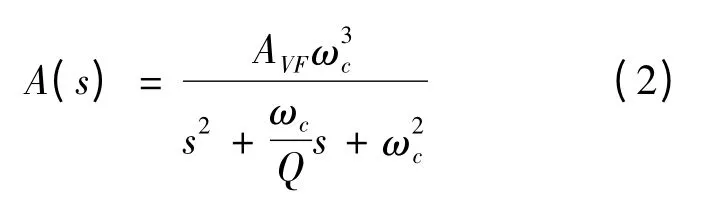
式(2)为二阶低通滤波器传递函数的典型表达式。其中:ωc为特征角频率;Q 为等效品质因素。

将二阶低通滤波器起串联形成N 阶低通滤波器，工程上常用查表式软件计算来确定参数，巴特沃斯低通、高通电路阶数N 与增益G 之关系见表1。

表1 阶数N 与增益G 的关系Table 1 Relationship of the order number and the gain

滤波器阶数越高越向理想特性逼近，本设计所采用的四阶巴特沃斯低通滤波器的设计原理图如图8 所示。

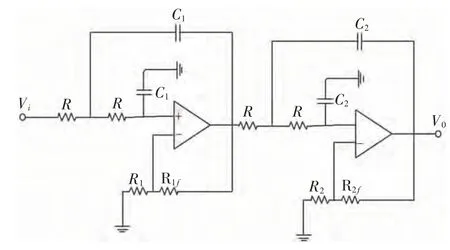
图8 四阶低通滤波器Fig.8 Fourth-order low-pass filter

设计的低通滤波器截止频率为fc=5.5 MHz，以AD8038 高速运算放大芯片为滤波电路的运放芯片。选取C1=C2=100 pF，根据可以得到R=289 Ω。现选取R1=62 kΩ，R2=20 kΩ，根据表1 增益可算出:R1f=(G-1)R1=(1.152-1)R1=9.42 kΩ;R2f=(G-1)R2=(2.235-1)R2=24.7 kΩ。仿真结果如图9 所示。

从图9 的仿真结果可以看出:截止频率为5.5 MHz(即最大幅值的处)，且通带平坦，效果良好且设计方案与仿真结果吻合。

2.2 四阶高通滤波器的设计

高通滤波电路的功能是将某一截止频率ωH以上的高频信号通过，而将ωH以下的信号给予衰减。图10 给出了四阶高通滤波器原理图。

选取C1=C2=100 pF，fc=4.5 MHz，根据fc=得R=526 Ω。现选取R1=62 kΩ，R2=20 kΩ，根据表1 增益可算出:R1f=(G-1)R1=(1.152-1)R1=9.42 kΩ;R2f=(G-1)R2=(2.235-1)R2=24.7 kΩ。仿真结果如图11 所示。

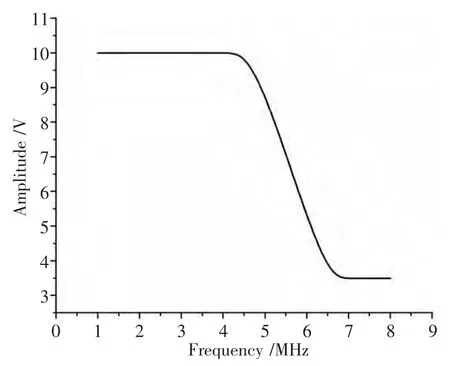
图9 四阶低通滤波器仿真图Fig.9 Simulation diagram of the Fourth order low-pass filter

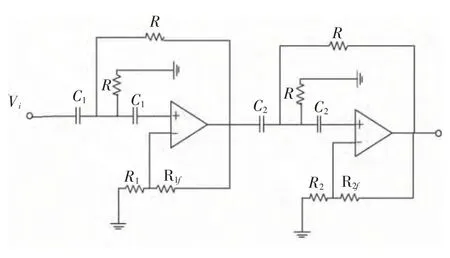
图10 四阶高通滤波器Fig.10 Fourth-order high-pass filter

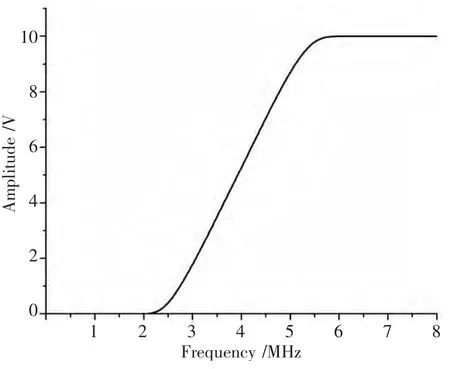
图11 四阶高通滤波器仿真图Fig.11 Simulation diagram of the Fourth order high-pass filter

3 结论

在非线性声学测量当中的高能RF 脉冲串不是单频成分，包含的旁瓣有可能扩展至谐频信号区域中。合适的换能器不能抑制杂散频率，也不能够抑制用于材料的非线性声学测量的大振幅的基频信号。正确设计的滤波器能有效抑制高功率电路所引入的非线性及发射脉冲串中的非线性进入接收系统。

1)设计并研制了一个截止频率为4.5 MHz高能高通滤波器系统成功的将幅值为2.2 V 的基波信号降至了0.01 V 左右，并将所需要的二次谐波信号幅值放大至2.1 V。

2)同时研制了一个截止频率为5.5 MHz 低通滤波器用于滤去高频成分的杂波，将幅值为0.35 V 三次谐波信号降至0.01 V 以下，实现了在大振幅信号中识别小振幅信号的功能，并抑制了仪器自身所产生的部分非线性因素。

3)要将该滤波系统应用在非线性声学检测系统中，则应该尽可能的减少不必要的元器件，且需要做好各元器件之间的屏蔽工作，避免由于过多元器件所带来的非线性信号。

［1］王彦骏.超声无损检测新技术的发展［J］.科技信息，2012(29):50.

［2］于广艳.非线性声学在材料缺陷识别中的应用［J］.北京电力高等专科学校学报:自然科学版，2012，7:373-375.

［3］王润田，章瑞铨，周艳，等.非线性声学的进展与应用［J］.声学技术，2007，26(2):348-356.

［4］Zheng Y，Maev R G，Solodov I Y.Review/Sythèse nonlinear acoustic applications for material characterization:A review［J］.Canadian Journal of Physics，2000，77(12):927-967.

［5］Rokhlin S I，Matikas T E.Ultrasonic characterization of surfaces and interphases［J］.Material Research Society Bulletin，1996，21(10):22-29.

［6］税国双，汪越胜，曲建民.材料力学性能退化的超声无损检测与评价［J］.力学进展，2005，35(1):52-68.

［7］敦怡，师小红，徐章遂.基于二次谐波技术的固体火箭发动机界面粘接质量的超声无损评价［J］.固体火箭技术，2008，31(2):198-200.

［8］陈斌.金属材料闭合裂纹和疲劳损伤的非线性超声检测技术研究［D］.北京:清华大学，2006:5-27.

［9］李志军，苏永新，王春华.电压模式双二阶跨导线性滤波器［J］.仪器仪表学报，2007，28(12):2214-2217.

［10］田大强，蒋平，唐国庆.有源滤波器中数字低通滤波器设计及其实现［J］.电工电能新技术，2003，22(3):77-80.

［11］姚福安，徐衍亮.高性能多阶有源带通滤波器设计［J］.电子测量与仪器学报，2005，19(2):20-25.

［12］康华光.电子技术基础(模拟部分)［M］.北京:高等教育出版社，2006:412-430.