基于细化谱和隐马尔科夫模型的齿轮故障分类方法

王文欢，王细洋，万在红

(南昌航空大学，南昌 330063)

0 引言

齿轮箱作为重要的传动部件，被广泛应用于各类机械设备中，因此对其进行故障诊断与分类的研究有着重要意义，是提高齿轮箱可靠性、减少停机检修时间的重要一环。振动信号常常作为介质来间接判断齿轮的当前运行状态，通过对比正常状态和故障状态振动信号的某些特征量，作为是否维修的决策依据，还可以判断不同类型的故障，如不平衡、转子碰磨、齿面磨损等。当齿轮出现故障时，会在频域上有所表现，出现各式各样的调制边频带，包含有丰富的齿轮故障信息，如果想对这部分频带进行细致分析，提取出影响结果的细微差别，则需要足够高的频率分辨率。细化谱分析是一种提高某特定频率段的分辨率的分析方法，能更精确的描述局部频率，Hoyer［1］和谢明［2］等在算法的改进和细化倍数的提高上作了很多的工作，使细化谱的性能更加优良。在细化谱分析法的应用上Hongzhong Ma［3］、段礼祥等［4］研究了细化谱分析法来诊断电动马达和泵阀的故障，孙伟等［5］把细化谱分析法用在齿轮故障诊断中，他们的共同缺点是需要有丰富经验的人员在较长时间做出决策，且缺乏对故障种类的判断。

隐马尔科夫模型具有很强的特征分类能力，已在语音识别等多个领域有成功的应用［6］，它所具有的两层随机结构与基于振动的故障诊断机理较为接近，通过可观测的振动信号来估计设备的隐藏状态。Baruah 等［7］详细地讨论了HMM 应用在金属切削刀具故障诊断和预诊断中一些的具体问题，并对算法作了修改，使之效率更高。Boutros等［8］研究了离散隐马尔科夫模型对铣刀的磨损状态的分类，同时也研究对轴承不同故障点的识别，两者成功率均较高。Zhu Kunpeng 等［9］把HMM 用在高速精细机床刀具磨损的监控中。鉴于轴承，各种刀具等信号与齿轮振动信号的类似性，将HMM 应用到齿轮的故障诊断中。

本试验将细化谱分析方法与HMM 的特征分类方法相结合，引入到齿轮箱故障分类中。该方法首先利用时域同步平均法对信号预处理，然后变换到频域，再对基频及其倍频处做细化谱处理，提取基频、倍频及其边频带幅值作为特征向量，输入到HMM 中，建立故障分类器，然后自动对故障类型作出识别。

1 HMM 建模

HMM 是一个统计学模型，是一个双重随机的过程:一重随机为马尔科夫链描述的状态之间的转移，是不可观测的;二重随机为状态中观测量的随机分布，可观测。HMM 包含有限个隐状态，状态根据其观察量的概率分布产生一系列观察量序列。一个HMM 可由如下参数描述［6］:

1)N:模型中马尔科夫链状态的个数。记N个状态为θ1，θ2，…，θN，t 时刻马尔科夫链的当前状态为q1，有qt∈(θ1，θ2，…，θN)。在实际应用中常常有着具体的物理意义。

2)M:每个状态中观察值的数目。记M 个观察值为v1，v2，…，vM，记t 时刻的观察值为ot，ot∈(v1，v2，…，vM)。观察变量对应这模型的输出，观察序列是在第二层随机的基础上给出，由观察变量组成。

3)π:初始状态概率分布向量。π=(π1，π2，…，πN)，式中πi=P(qt=θi)。

4)A:状态转移概率矩阵。A=(aij)N×N，式中aij=P(qt+1=θj｜q=θi)，1≤i，j≤N。

5)B:观察值概率矩阵。B=(bjk)N×M，式中bjk=P(ot=vk｜qt=θj)，1≤j≤N，1≤k≤M。

一个HMM 可以用以上5 个参数表示，记为λ=(N，M，π，A，B)，N 和M 在HMM 中对模型训练影响不大，一般选定后可将其作为一个常量，所以简写为λ=(π，A，B)。

实验中采集的数据是一系列离散的点，通常不会把这些点直接作为HMM 状态的特征量，数据太多会导致主要特征淹没其中，计算量会明显增大;因此，需要选择一个对故障敏感的特征量，以前的研究表明频率成分的变化是故障敏感的，可以用细化谱分析特定频带提取特征量，进行故障分类。

2 时域同步平均和细化谱算法

2.1 时域同步平均(TSA)

时域同步平均法是一种很有效的信号预处理方法，在齿轮的振动信号的分析中应用广泛，它可以从复杂的齿轮箱外部采集的振动信号中提取目标齿轮振动信号。TSA 的原理是:通过与目标齿轮的转频同步，多段信号累加，再平均而得到TSA信号，可以消减非目标齿轮以外的信号和背景噪声，提高信噪比，达到提取目标齿轮振动信号的目的。

假设有一段多圈的采样信号S(1，2，…)，它的TSA 信号表示为

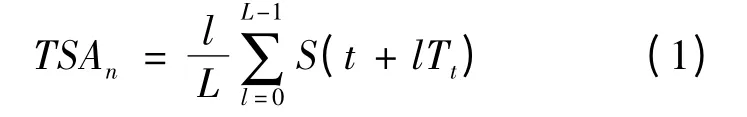
其中，L 为平均的圈数，Ti为一圈采样的点数［8］。因为齿轮箱里不同齿轮转一圈采样的点数不同，也就是Tt不同，就可以对不同的齿轮作TSA 处理，提取出目标齿轮的信号。

2.2 复解析带通滤波器的细化谱理论

1)构造FIR 非递归复解析带通滤波器。

需要构造的复解析带通滤波器的幅频特性如图1 所示，其中f 为采样频率的一半，通带宽为ω2-ω1，ωe为通带的中心频率，由于缺少负频率部分，令正频率通带处的频率幅值为2。为了构造解析带通滤波器，需先作一个实低通滤器，其冲击响应函数为

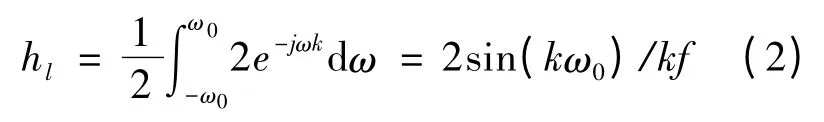
再对低通滤波器进行复移频，即可得到该解析滤波器，其冲击响应为

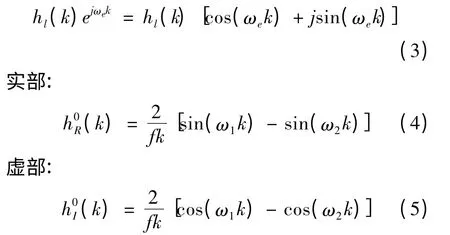
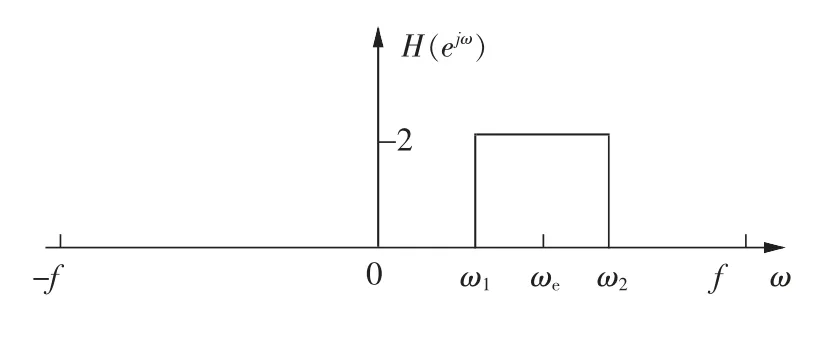
图1 幅频特性Fig.1 Amplitude-frequency characteristic

2)复解析带通滤波器复调制细化谱分析方法［2］。

记原始信号的采样频率为fs，N 为傅里叶变换分析的点数，D 为细化倍数，M 为滤波器的半阶数，采样序列为x(n)(n=0，1，…，DN +2M)。则实现复解析带通滤波的细化谱分析法的步骤是:首先构造复解析带通滤波器宽度为fs/D，再隔D点选抽一点、移频，然后作N 点谱分析，最后把频带f1～f2用N 条独立谱线来表示。

具体分解为以下5 个步骤:

①给定细化倍数与中心频率。按实际需要给定细化频段的细化倍数D 与中心频率fe。

②构造复解析带通滤波器，滤波器的冲击响应为h0(n)，宽度为fs/D。

③选抽滤波。采用前一步构造好的滤波器h0(n)对序列信号x(n)做选抽滤波，选抽出N点，选抽比为D。选抽的点数与FFT 运算的点数都是N 点。用复解析带通滤波器可以将滤波和选抽两个过程结合起来计算，以提高效率。实信号经过滤波器后，变成频率在通带以内的复解析信号。记选抽后的复信号为g(m)=y(Dm)。

④复调制与移频。对选抽后的复信号g(m)需要做复调制移频，即将细化后的起始频率移到零频率点，得到g'(m)=g(m)e-jω1m，(m=0，1，…，N-1)。

⑤对g'(n)作N 点的FFT 与谱分析，不需要进行频率范围的调整，就可以得到具有N 条独立谱线的细化后的频谱。

3 HMM 故障诊断试验

试验采用单级减速齿轮箱为实验对象，对4种状态进行了实验，即3 种齿轮常见故障状态和1 种正常状态。整个装置由同步转速为1 750 r/min、额定动率为4.5 kW 的交流电动机驱动，并在终端连接一电动机作为负载，其额定功率较电动机大(图2)。电机的转速由数字矢量驱动单元控制，其负载也是通过类似单元控制发电机电流来控制负载大小。采用基于虚拟仪器平台搭建的数据采集系统。

对各种故障进行模拟实验，主动轮齿数为21，从动论齿数为70。预加载的扭力为73 N·m。人为制造故障特征后，再放到实验台上运行，每隔10 min 作一次采集，采用编码器控制采集，使每次开始采集的相位都一致，数据的采集宽度为10 s，采样频率为20 kHz。信号经10 倍增益、A/D 转换，再存储。每个数据文件含20 万个采样点。实验台集成加速度式振动传感器、编码器器、扭矩传感器及速度传感器等。根据参数计算得到啮合频率为612.5 Hz。

图2 实验系统Fig.2 Test setup

3.1 数据的预处理和特征的提取

实验中的传感器安装在齿轮箱表面，齿轮径向的加速传感器采集的信号对齿轮故障最为敏感，故以此传感器采集的数据为研究对象。采集得到的原始信号因含有噪声且衰减严重，需要用时域同步平均技术来提高信噪比。图3 为TSA预处理信号，从原始信号的频域图中看到频谱比较杂乱，经过时域同步平均后单个齿轮的啮合频率非常明显，经FFT 变换后求得啮合频率为612.7 Hz，与理论的频率一致，并且出现二倍频和三倍频，对基频和各级倍频处做细化谱(Zoom-FFT)处理(图4)，可以看出在主要频率附近出现了不同大小的对称或者不对称的调制边频带，根据之前的研究［4-5］，齿轮箱的状态与基频及各级倍频及其边频带有一定的关系。齿轮箱状态由正常到故障，边频带也会从无到有，最后逐渐增大，不同种类的故障会使频谱出现不同的种类和大小调制边频带。

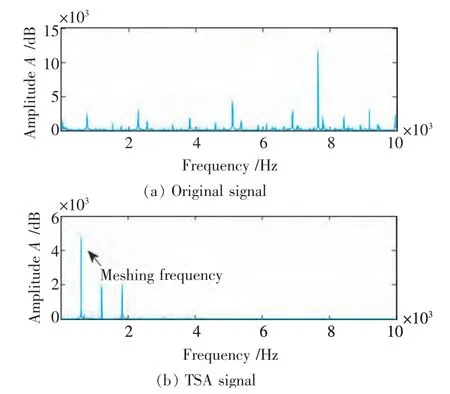
图3 TSA 预处理Fig.3 TSA preprocessing

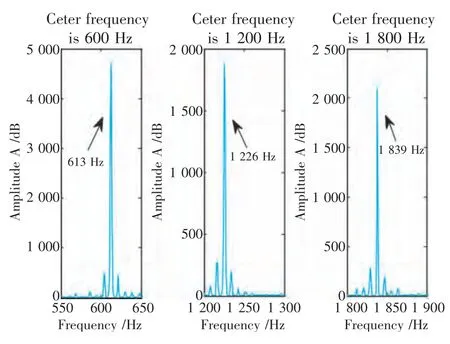
图4 信号的细化谱分析Fig.4 The ZOOMFFT spectrum of signal

3.2 HMM 建模

以试验采集的数据作为基础，采用3.1 节介绍的数据预处理方法，从中提取特征向量来训练和验证HMM。试验采用一阶齐次马尔科夫模型描述隐状态，假设特征量彼此相互独立，每一个模型代表一种齿轮状态。采用EM(Expectation Maximization)算法为每种故障状态和正常状态建立模型，通过Viterbi 算法计算特征向量在4 个HMM 下的输出概率，以此判断该特征向量所属的模型，图5 给出了处理过程模型。

3.3 试验分析

试验中共有4 组数据对应正常、不平衡、裂纹和点蚀4 种状态。每组采集的文件个数不一样，分别采集122、112、172、180 个。每组数据的一半用于训练，另一半用于验证。对每个文件的数据先进行TSA 去噪处理，后作FFT 变换，最后进行细化谱分析提取基频、倍频及其边频带幅值，归一化后，统一量化处理，量化精度为40。

用交叉验证寻找最优状态数，当HMM 的隐状态数选为5 时误差最小。设置收敛误差为，最大迭代次数为50，4 种模型的迭代次数与每次迭代的对数似然概率见图6，随着迭代的进行，4 种模型的对数似然概率也在不断增加，在25 步内达到收敛误差，收敛快速。

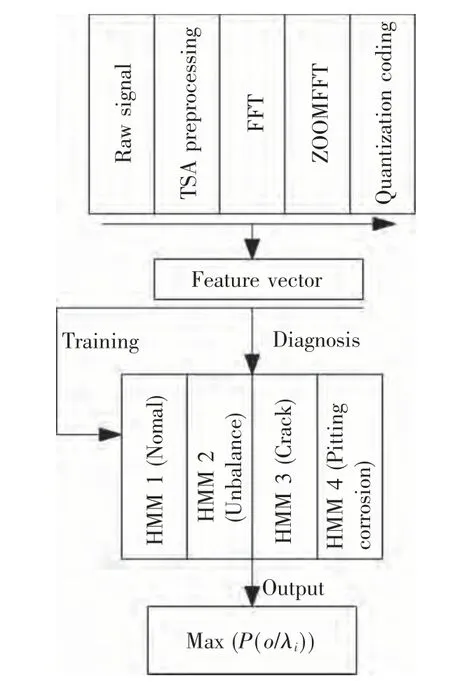
图5 特征提取和HMM 诊断模型Fig.5 Feature Extraction and HMM based on diagnostic model

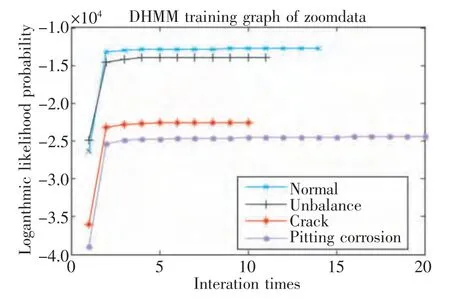
图6 HMM 训练图Fig.6 Training graph of HMM

各种状态的模型建立以后，用各组数据的另一半来诊断故障，验证模型的准确性。4 组数据的另一半提取特征向量后分别输入到建立好的4种模型中，模拟实验测试的统计结果见表1。从表中可知，在有限次的实验中，出现了极少数的不成功诊断，例如在正常的61 次实验中，有58 次作了正确的诊断，2 次误诊断为裂纹，1 次误诊断为点蚀，成功率为95.08%，分类结果较为理想。在其他故障的诊断中，也只出现了极少次的诊断错误，平均成功率达到了95.56%，在实际的诊断中通过多次采集数据和诊断，基本可以确定故障类型，诊断精度较高。

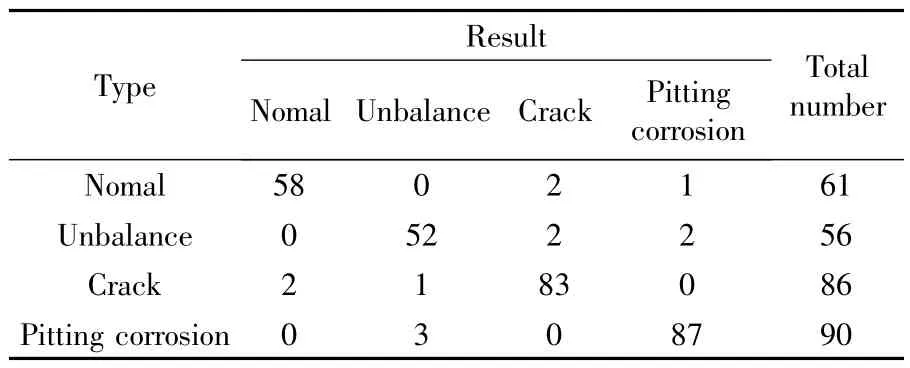
表1 故障诊断实验结果Table 1 Result of experiment

4 结论

1)以齿轮的振动信号作为研究对象，利用时域同步平均法准确地抽取目标齿轮的特征信号。

2)引入了基于细化谱的特征提取方法，对感兴趣的频带进行细化处理，能更准确地反应频谱的微小变化。

3)应用HMM 进行了齿轮的故障种类识别，采用交叉验证获取最优状态数，并通过齿轮箱试验系统验证了该方法的有效性。

［1］Hoyer E A，Stork R F.The zoom FFT using complex modulation［C］.Acoustics，Speech，and Signal Processing，IEEE International Conference on ICASSP '77，1977，2:78-81.

［2］谢明，丁康.基于复解析带通滤波器的复调制细化谱分析的算法研究［J］.振动工程学报，2002，15(4):479-483.

［3］Ma H Z，Xu Q，Song J G，et al.The application of zoom FFT technique to the extraction of fault character of induction motor［C］.Condition Monitoring and Diagnosis，2008.CMD 2008.International Conference on，2008:221-225.

［4］段礼祥，张来斌，王朝晖，等.往复泵泵阀故障的细化谱诊断法［J］.仪器仪表学报，2004，25(4 增刊):568-570.

［5］孙伟，王细洋，徐英帅.基于复解析带通滤波器的ZOOMFFT法应用于齿轮故障诊断［J］.组合机床与自动化加工技术，2011(10):57-59.

［6］Rabiner L.A tutorial on hidden Markov models and selected application in speech recognition［J］.Proceedings of the IEEE，1989，77(2);257-286.

［7］Baruah P，Chinnam R B.HMMs for diagnostics and prognostics in machining processes［J］.International Journal of Production Research，2005，43(6):1275-1293.

［8］Boutros T，Liang M.Detection and diagnosis of bearing and cutting tool faults using hidden Markov models［J］.Mechanical Systems and Signal Processing，25(6):2102-2124.

［9］Zhu K P，Wong Y S，Hong G S.Multi-category micro-milling tool wear monitoring with continuous hidden Markov models［J］.Mechanical Systems and Signal Processing，2009，23(2):547-560.