螺旋桨建模方法及敞水性能研究❋
2014-11-28黄璐陈立
黄 璐 陈 立
(中国舰船研究设计中心 武汉 430064)
1 引言
船舶螺旋桨作为在现代船舶上应用最为广泛的推进器,其性能的优劣在整个船舶设计过程中具有举足轻重的地位。在螺旋桨的设计和制造过程中,预报水动力性能、强度校核以及数控加工都是基于高精度的几何体建模。螺旋桨曲面形状复杂,故探究合理的螺旋桨建模方法可以为后续工作打下坚实的基础。
本文以DTMB4119桨为模型,讨论了螺旋桨的两种建模方法,分别是坐标转换法和缠绕法。坐标转换法通常是已知螺旋桨桨叶切面形式以及叶切面六个参数:螺距、纵斜、侧斜、弦长、拱度、最大厚度。通过相应的坐标转换公式,将以型值表形式表达的螺旋桨叶切面的局部坐标转换为全局坐标,采用点—线—面—体的顺序依次完成建模。缠绕法通过建立螺旋线的展开图,确定每个螺旋桨叶切面在展开图中的正确位置,根据位置的对应关系将其缠绕到圆柱面上,从而获得真实空间的叶切面。其关键在于正确确定螺旋桨叶切面展开图的位置。为了验证和比较两种建模方法的精度,基于计算流体力学基本理论,借助商业软件Fluent,分别对两个模型进行了水动力性能预报。
2 坐标转换法螺旋桨建模
2.1 坐标转换法原理
坐标转换法螺旋桨建模主要在于将桨叶型值点从平面坐标转换到空间坐标。通过已知的螺旋桨叶切面型值点和相关几何参数,选择恰当的数学模型,将二维的型值坐标转换成三维的型值点。坐标转换通常是通过高级语言程序的编写来实现。
选取DTMB P4119桨[1]进行建模,其几何参数如表1所示。

表1 DTMB P4119螺旋桨的几何参数
2.2 坐标转换
用半径为r的圆柱去截取螺旋桨后的展开图[2],如图1所示。
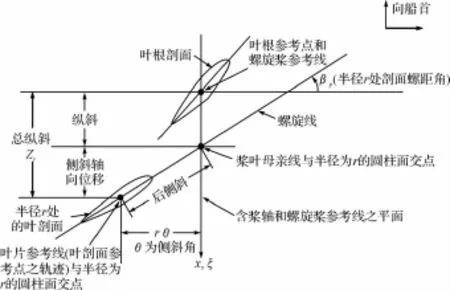
图1 半径为r的圆柱面展开后的平面
根据图1所示几何关系可以推导出桨叶表面的参数化方程。桨叶拱弧面三维坐标表达式为

式中:r为叶剖面半径,XR(r)为初始纵倾;θs(r)为侧斜角;φ(r)为叶剖面螺距角;C(r)为叶剖面弦长;s为无量纲的弦长,导边处为0,随边处在1;剖面s处拱弧线纵坐标,厚度为t。
参考NACA切面半厚度及拱弧线分布表,结合坐标转换公式,通过Fortran编程进行坐标转换,换算出螺旋桨曲面型值点的三维空间坐标[3~4]。
2.3 螺旋桨几何模型生成
1)三维型值点输入,将各叶切面型值点空间坐标导入到三维绘图软件中。
2)通过点创建曲线功能生成叶切面空间曲线。
3)将曲线放样成螺旋桨的叶面和叶背。
4)将放样曲面和底面缝合成一个实体。
5)通过桨毂型值点,建立桨毂的模型,圆周阵列,以X轴为旋转轴复制,得到桨叶实体。

图2 螺旋桨桨叶建模

图3 坐标转换法螺旋桨模型一
3 缠绕法螺旋桨建模
3.1 缠绕法原理
缠绕法[5~8]的原理是将螺旋桨叶切面缠绕到相应半径相应位置的圆柱面上。通过螺旋桨叶切面曲线展开的二维图来生成三维曲线,如图4所示。
3.2 螺旋桨几何模型生成
1)螺旋桨叶切面尺寸检查及叶切面曲线创建,如图5所示。

图4 螺旋桨叶切面螺旋线缠绕后的空间曲线

图5 叶切面伸张曲线图
2)各半径叶切面曲线旋转及包络,如图6所示。
3)构造螺旋桨叶面及实体生成,如图7所示。

图6 旋转相应螺距角后叶切面曲线

图7 缠绕法螺旋桨建模二
4 螺旋桨水动力验证
为了进一步验证和比较两种建模方法的正确性和精确性,通过CFD商业软件对螺旋桨模型的水动力性能进行数值模拟[9]。
4.1 流体网格划分
对整个计算域进行分区网格划分,可以精确地获取螺旋周围流场的信息,避免流场变化平缓区域的计算资源浪费。取计算域为直径5D,长度12D的圆柱体,此为静流域。同时,建立直径2D,长度1.5D的小圆柱体作为动流域。对于动流域,采用适应性良好的三角形网格对桨叶与桨毂连接处以及叶梢进行局部加密,以便捕捉到重要的流场信息。对于静流域,采用结构网格适当降低密度[10]。

图8 桨叶叶面网格划分图

图9 螺旋桨及整个流域网格划分图
4.2 边界条件设置
进口边界条件设置为速度进口,给定相应进速系数下的速度。出口边界条件设置为压力出口。圆柱体的侧面设置为壁面边界条件,壁面为无滑移固壁条件。由于静流域和动流域的表面网格不一致,在fluent中无法传递计算,将交界面设置成interface边界条件,从而两边不同的网格通过此面进行信息传递。动流域的运动形式为MRF,绕X轴旋转。静流域与螺旋桨静止水中相同,仍为静止流体。
4.3 敞水性能曲线计算结果与实验对比
螺旋桨旋转速度设置为10rad/s,在设计进速系数J=0.833左右两边分别取J=0.5,J=0.7,J=0.9,J=1.1,选取SST湍流模型进行模拟,求得不同进速系数下的推力和扭矩,进而求得推力系数KT、转矩系数KQ及敞水效率。将模型一和模型二的计算值与实验值绘制成图,如图10所示。
由敞水性能曲线可以看出,计算值与实验值吻合较好,说明了两种方法有较好的建模精度。根据数值模拟结果还可以看出,同一网格划分方案以及同一求解设置下,缠绕法的计算精度较坐标转换法略高,其原因可能是因为各叶切面曲线建立时对数据进行了检查,修改了不准确的数据,而且,缠绕的方式完全符合螺旋桨叶面的成型特点。模型一和模型二计算所得的推力系数、转矩系数、敞水效率的平均相对误差除了J=1.1处均在2%以内。关于J=1.1时的误差原因是,因为螺旋桨在相同转速和直径下,进速系数越大,来流速度越大,但相应的推力和扭矩越小,所以小干扰就会导致试验值和计算值之间很大的误差。

图10 螺旋桨敞水性征曲线
4.4 螺旋桨表面压力分布
根据模型的计算结果作出螺旋桨表面压力分布云图,图11为敞水计算结果更为精确的缠绕法计算出的压力分布云图。由图可知,螺旋桨压力从随边到导边逐渐增大,并在导边处达到最大值。在设计进速系数下,叶面的压力从叶根到叶梢,不断增加,达到一定值后,然后逐渐减小,在叶梢处达到最小值,叶背总压由负值向正值变化[11]。

图11 桨叶表面压力分布云图
5 结语
1)基于坐标转换法的螺旋桨三维建模,通过桨叶叶切面局部坐标到全局坐标的转换,实现了螺旋桨的三维实体建模。基于缠绕法的螺旋桨三维建模,通过桨叶切面展开图的缠绕包络,利用二维图生成三维曲面,还原了真实的桨叶截面。由于缠绕法符合螺旋桨叶面成型的原理且建立叶切面曲线时进行了数据检查,建模精度高于坐标转换法。
2)基于计算流体动力理论,对两种方法建模得到的螺旋桨模型分别进行了水动力性能预报。通过计算值与实验值对比,验证并比较了两种建模方法的精确性。同时,也验证了螺旋桨水动力性能的数值预报已具有较高的精度。
[1]KO YAMA K.Comparative calculations of propeller by surface panel method—workshop organized by 20th ITTC propulsion committee[J].Papers of Ship Research Institute,1993,15(Supplement):57-66.
[2]王国强,董世汤.船舶螺旋桨理论与应用[M].哈尔滨:哈尔滨工程大学,2009.
[3]肖冰,石爱国,王骁.基于GAMBIT的舰船全附体几何建模[J].船舶工程,2012,2(32):33-35.
[4]高富东,潘存云.复杂曲面螺旋桨实体模型参数化设计与分析[J].机械科学与技术,2011,1(30):1-5.
[5]孙娜.船用螺旋桨的曲面造型及加工仿真研究[D].大连:大连理工大学,2010:26-39.
[6]陈艳锋,吴新跃.螺旋桨桨叶计算机实体造型方法研究[J].海军工程大学学报,2005,17(4):104-107.
[7]王军.三叶螺旋桨的CAD建模与数据验证[J].制造业自动化,2012,7(34):52-59.
[8]申毅莉.船用螺旋桨桨叶建模分析研究[J].组合机床与自动化加工技术,2013,4(4):113-117.
[9]姚震球,高慧,杨春蕾.螺旋桨三维建模与水动力数值分析[J].船舶工程,2008,30(6):23-26.
[10]钱卫东,吴成才,冷文浩.螺旋桨自动化几何建模和网格划分技术[J].舰船科学技术,2011,3(61):39-43.
[11]YOUNG Y L.A BEM for prediction of unsteady midchord face and/or back propeller cavitation[J].Journal of Fluids Engineering,2001,6(123):311-319.
