基于局部线性重构的全景高光谱影像低维可视化

❋

何 军1 李滋刚2

（1.南京信息工程大学电子与信息工程学院 南京 210044）（2.东南大学仪器科学与工程学院 南京 210096）

1 引言

近年来，随着传感器技术和计算机技术的飞速发展，人们对于空间数据分析逐渐由全色波段、多光谱的栅格数据转向更高维的高光谱影像。然而，光谱数据维度的提高却给空间数据的分析带来了极大的困难，这就是数据分析领域的维度灾难问题（Curse of Dimensionality）［1］——即在保持一定取样密度所需样本的个数随着数据空间维度的增加成指数级增加，而且散布在外围的样本数也随着空间维数的增加成指数级增加，并且还表现为模型的复杂程度或模型的表示长度随维数成指数级增加。为了克服维度灾难给空间数据处理带来的困难，我们希望能够用低维的坐标以近似等价的方式去刻画原来的高维空间中的数据。PCA（Principle components analysis）［2］和 MDS（Multi－dimensional scaling）［3］等线性算法能够有效发现线性子空间，且在数据内插、外推、压缩、去噪以及可视化等方面的应用已经被证明是非常有效的。由于PCA方法假设数据的固有结构是线性的，即PCA的本质是建立在全局线性假设之上，而高光谱数据中含有较多的非线性［4～6］，数据的分布呈现明显的弯曲，不能再近似地认为高光谱数据取自线性子空间。因此，若要对高维空间数据进行更为准确的分析，需要研究发现非线性结构的方法。

近年来美国海军研究实验室的Bachmann博士等学者，首先基于非线性低维流形思想对于高光谱数据进 行 建 模［7～9］，并 取 得 了 非 常 显 著 的 成果［10］。在Bachmann的工作启发下，从扩散过程的角度出发，利用扩散映射思想［11～12］对高光谱数据的低维表示也展开了研究工作［13～14］。相对于传统的线性表示技术，非线性的数据表示技术带来的问题是较高的计算复杂性，难以处理的海量的数据。目前较为流行的一种方法是首先将大尺度的高光谱影像进行分片，对每个分片分别进行非线性降维，从而得到各自在流形上的内蕴坐标表示，然后选择一个分片作为基准，并基于坐标系对准的思想，将其它分片的流形坐标映射到这个基准坐标系统中［9，13］。本文提出一种新的基于局部线性重构的扩散坐标系延拓算法，即对于海量的外采样点（Out－of－sample），直接通过局部线性重构算法找到它们在扩散坐标系的坐标表示，这种新的方法相对于基于坐标系配准的延拓方法，高光谱影像数据在扩散坐标系下的表示更为一致。

2 扩散映射与局部线性重构算法

2.1 扩散映射

通过研究图或流形上的扩散过程，进而发现蕴含在高维数据集中的信息，是Yale大学扩散几何小组近年来发展起来的对于高维数据分析的理论［11］。扩散映射（Diffusion Maps）［12］算法简单描述如下：

把数据集视为由数据作为顶点做构成的邻接图，数据与数据之间的边的权重k（x，y）满足如下的对称半正定性质：

·k是对称的：k（x，y）＝k（y，x）；

·k是正保持的：对于数据集X中所有的x和y，都有k（x，y）≥0；

·k是半正定的：即对于定义在X上所有的实有界函数f，均有：

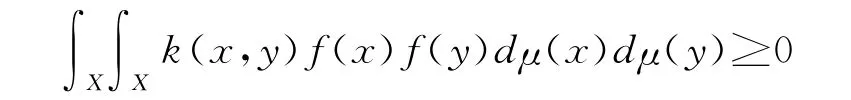
这里μ是X上的概率测度。

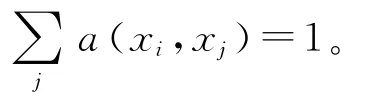
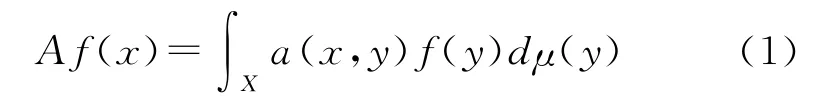
对于对称化后的扩散算子˜A和扩散核˜a（x，y），有如下的谱分解：

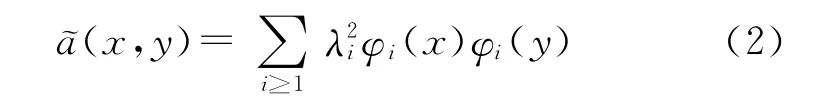
其中特征值满足λ1＝1≥λ2≥λ3≥…。对于第m次扩散时刻的扩散算子˜Am及对应的扩散核˜a（m）（x，y），则有

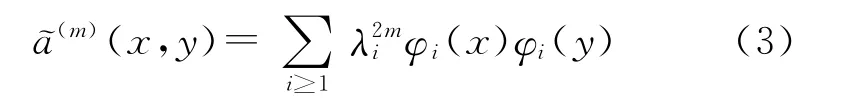
因此，可以引入如下的一族扩散映射｛Φm｝：

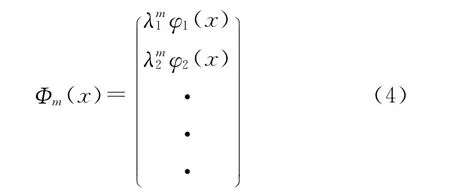
对于高光谱影像在扩散几何坐标下的可视化表示而言，该族扩散映射能够将高光谱数据集Γ中任一x嵌入至低维的扩散空间：

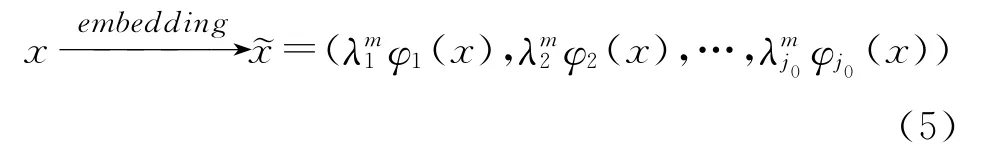
其中j0是在不引入明显误差情况下，所嵌入扩散空间的维度。由扩散映射理论可知，扩散空间把握了特征空间内蕴几何结构，因此我们将此低维坐标表示称之为高光谱数据的扩散几何坐标［13］。

2.2 局部线性重构算法

对于规模诸如O（106）的全景高光谱影像构造扩散映射，直接计算无论是运行内存还是运算时间均不可行。因此一种有效的解决方法是首先在少量采样（In－Sample）的高光谱数据集上构造扩散映射，然后建立起由外采样点（Out－of－Sample）到扩散几何坐标的映射关系，利用该映射能够近似得到外采样点的扩散坐标。这里我们引入局部线性重构算法（Local Linear Reconstruction）能够建立起外采样点和已经构造好的扩散坐标系之间的映射。局部线性重构算法的示意图如图1所示。

对于高维数据集合Γ⊂RD，假定Γ分布在RD中的低维流形M 之上或附近，将Γ分为两个子集合Γ1和Γ2，其中Γ1＝｛x1，x2，…，xn｝，Γ2＝｛xn＋1，xn＋2，…，xN｝∈RD，由Γ1构造出扩散映射Φ：RD→Rd，其中d≤D，使得yi＝Φ（xi），i＝1，2，…，n，这里yi对应于xi在扩散空间中的扩散坐标。相对于x1，x2，…，xn，xn＋1，xn＋2，…，xN称之为外采样点。对于Γ2的数据点xj，j＝n＋1，…，N，无法直接套用Φ得到对应的yj，因为Φ并没有显示的表达式，它蕴含在特征值求解过程。由于Γ1和Γ2分布在相同的低维流形M之上或附近，因此借助于局部线性假设，我们可以把Γ2中任一数据点xj放入Γ1中，并找到xj在Γ1中的局部邻域｛xj1，xj2，…，xjk｝，在该局部邻域内xj可由｛xj1，xj2，…，xjk｝线性表示，而线性表示的系数｛Wj1，Wj2，…，Wjk｝在嵌入空间保持不变，于是yj能够利用此重构系数计算得出。具体算法描述见算法1。

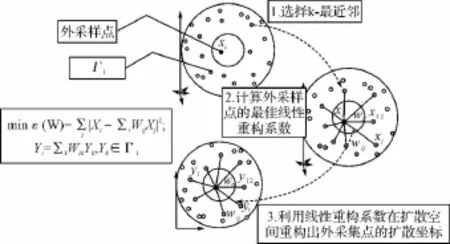
图1 局部线性重构算法

算法1 局部线性重构算法

Step 1.对集合Γ1构造扩散映射Φ：RD→Rd，得到Γ1在Φ 作用下的像｛y1，y2，…，yn｝；

Step 2.将Γ2中每一数据点xj在Γ1中进行最近邻居搜索，如kNN搜索，得到Γ1中与xj在欧式距离意义下的若干最近邻居｛xj1，xj2，…，xjk｝；

Step 3.根据xj在Γ1中的近邻｛xj1，xj2，…，xjk｝，计算线性重构的权值Wjk，使得

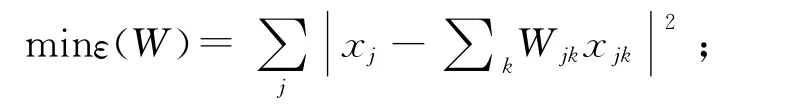
Step 4.由计算所得的重构权值Wjk和邻域对应的扩散坐标｛yj1，yj2，…，yjk｝，重构出yj，即：

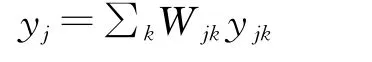
3 基于局部线性重构的扩散坐标系延拓算法

在以往的工作中［13］，利用局部线性重构方法可以得到分片中的部分点在骨干（Backbone）的扩散坐标系下的近似坐标表示，进而构造了分片扩散坐标系与Backbone扩散坐标系之间的坐标变换矩阵，但是由于局部线性重构方法构造的两个坐标系之间的近似对应关系，因此坐标变换的方法并不能保证把各个分片精确地统一到Backbone的扩散坐标系，所以在最终拟合的全景高光谱扩散坐标中分片与分片之间存在不连续性。

在我们最近的研究工作中，发现只要构造了Backbone并计算出Backbone的扩散坐标系，那么对于全景高光谱影像中的任何数据点，均能用局部线性重构的方法在Backbone的扩散坐标系下重构出该点对应的扩散几何坐标，所以如果对Backbone之外所有的数据点做同样的计算，不仅能够成功地得到全景高光谱影像的扩散几何坐标表示，而且解决了不连续性的问题。因此，本节提出了基于局部线性重构的扩散坐标系延拓算法，该算法的关键之处在于两点，第一是Backbone的构造，第二则是把除了Backbone之外的数据点，即外采样点，“插入”至Backbone的扩散坐标系下，“插入”的方法就是“局部线性重构算法”。

3.1 骨干坐标系（Backbone）的构造

在本扩散坐标延拓算法中，仅需直接计算出Backbone的扩散几何坐标，外采样点的扩散几何坐标不需直接算出，这些外采样点将由局部线性重构算法被“插入”至Backbone的扩散坐标系。因此Backbone的选择非常重要。

从局部线性重构算法知道Backbone的选择取决于两个因素，即Backbone对高光谱特征空间的覆盖性和计算可行性。这里引入一个假设，即全景高光谱影像的特征空间相对样本空间的稀疏性假设。我们知道，全景高光谱影像是遥感设备对一个地区地表物质光谱吸收和反射情况的测量。样本空间的大小size（S）对应于遥感设备的空间分辨率，而特征空间的大小size（F）取决于观测地区地表成分的复杂程度。很显然，对于O（106）分辨率而言，样本空间的大小size（S）＝O（106），而绝不会出现该地区的地表任何一处都是不同的成分，即size（F）≪size（S）。

为了使得采样S′能够较好的覆盖S，我们引入ε－net的概念，即定义在S中的子集S′，所有点均满足ε－net要求，也就是说S′中的任何两个点xi、xj之间的距离均大于ε，而对于S中的其它的点y，在S′中存在至少一个点x到y的距离小于ε。ε－net的概念在图2做了直观的解释。基于ε－net可以设计出更为有效的随机采样算法，即算法2随机εnet采样方法。

图2 ε－net示意图

算法2 随机ε－net采样方法

采样算法执行的过程就是构造ε－net的过程。随机选择x0∈S；由归纳法，对于k≥1，假设已经选择了x0，x1，…，xk∈S，使得所选择的任何两个点之间的距离均不小于ε。令

表示采样k个点后，在S中挖去k个ε－球后的剩余空间。如果Rk为空集，则算法停止，否则继续从Rk中选择点xk＋1。

由Rk的定义可知，xk＋1与x0，x1，…，xk之间的距离必然不小于ε。因此当构造ε－net的过程结束时，也就是说当第k＊个点被选中后，那么对于任意的y∈S我们都能在S′中找到一个点x，使得这两个点之间的距离不超过ε，否则的话则有y∈Rk，上述构造过程不会停止。因此，算法2保证了随机采样很好地覆盖了原样本空间。

3.2 外采样点在骨干坐标系上的局部线性重构

基于局部线性重构算法，依据高维数据集中嵌入低维流形结构的假设和局部线性思想，能够得到外采样点在低维流形上的参数化表示。另外，由于我们采用ε－net随机采样所构成的Backbone能够较好地逼近全景高光谱影像的特征空间，因此Backbone同样能够较好逼近全景高光谱影像的低维流形，计算得出的Backbone扩散几何坐标则是对该低维流形结构的参数化表示。于是对于Backbone之外的外采样点，每一个点均可以利用局部线性重构算法得到该点在Backbone扩散坐标系下的坐标表示，算法的示意图见图3，具体算法步骤见算法3。

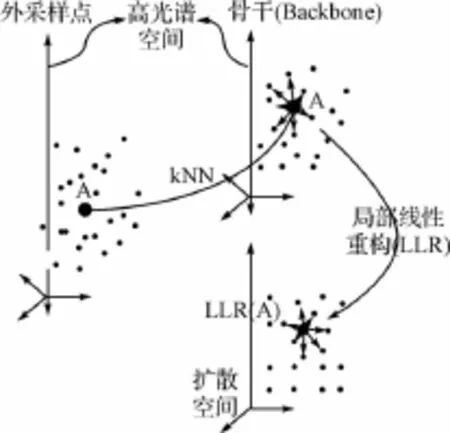
图3 外采样点在Backbone上的局部线性重构

算法3 基于局部线性重构的扩散坐标系延拓算法

Step 1.使用算法2介绍的ε－net随机采样方法对规模为｜S｜的全景高光谱影像S进行采样，构造出S的Backbone S′，并使用二维数组B记下S′在S 中的标号（i，j）；

Step 2.对Backbone S′构造扩散映射ΦS′，并由此得到Backbone的扩散坐标系｛φ1，φ2，…，φd｝S′；

Step 3.对于外采样点SO∶＝S＼S′中每一个点x，执行如下子过程，并同时将SO在S中的标号记入二维数据B；

Step 3.1 利用近似最近邻居搜索算法在S′中搜索x的k个最近邻居x1，x2，…，xk，求解如下方程

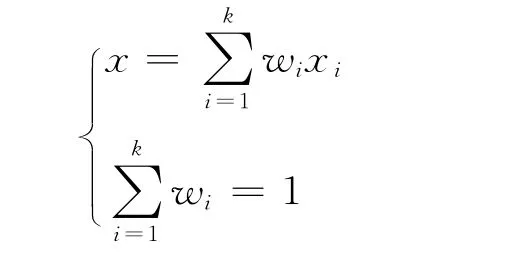
从而得到在k－邻域内x的局部线性表示；

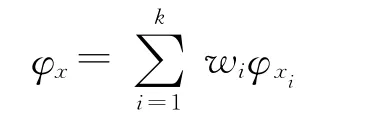
Step 4.将重构出的SO的扩散几何坐标与Backbone S′的扩散几何坐标按照其在全景高光谱影像S中的标号顺序进行排列，即完成该算法。

4 实验效果

针对NASA所公开的AVIRIS系统所采集的高光谱影像进行实验。这里选择AVIRIS系统在1997年在Moffet地区采集的高光谱影像的第二景（Scene）数据。该景影像的分辨率是614×512，含有224个近似连续的波段，波段范围从0.369μm～2.506μm，根据AVIRIS的说明，在这224个波段中存在大约30个完全吸收和噪声波段，在此实验中将此30个波段排除。实验平台是Intel Core i5CPU 2.3G，8G内存，Mac OSX 10.6操作系统，基于 Matlab2010b所实现的算法。

4.1 骨干（Backbone）坐标系的实验确定

图4 AVIRIS高光谱影像ε－net随机采样ε选择与采样比率的曲线

图5 ε设置为0.48时Backbone在波段1和波段60的投影

首先需要确定的是Backbone。这里采用ε－net随机采样方法，因为ε－net在较小的采样率情况下，能够很好地覆盖原样本空间，所以对AVIRIS高光谱影像进行ε－net随机采样实验，确定合适的ε。对于该高光谱影像，ε取值与所采样数据点的规模曲线如图4所示，可以看到当我们将ε减小到0.6时，采样规模迅速上升，对应于采样的密度越来越大。这里我们将ε设置为0.48，图5展示了采样所得Backbone在波段1和波段60的分布情况，能够很好地逼近原高光谱特征空间在这两个波段的投影。

4.2 AVIRIS高光谱影像的全景可视化

当ε设置为0.48时我们采样所得Backbone由6827个点组成，由扩散映射算法［12］，计算Backbone的扩散坐标系。由于一次性读入全景高光谱影像会造成庞大的内存开销，因此将高光谱影像划分为7×7个分片，分别逐次地应用局部线性重构算法，求出所有外采样点在Backbone扩散坐标系下的坐标表示，这里同样设置最近邻居搜索的参数k＝10，扩散空间的维度为15。基于算法XX将Backbone扩散坐标系延拓至全部的外采样点，得到全景高光谱影像的扩散几何坐标表示，其中进行ε－net随机采样的耗时为10.5s，计算Backbone的扩散几何坐标的耗时为3.1s，通过局部线性重构算法将外采样点延拓至Backbone扩散坐标系的耗时为57.6s。由以上参数设置计算得出在扩散坐标系下高光谱影像的表示如图6和图7所示，其中图6是由扩散几何坐标（φ2，φ3，φ4）所构成的RGB彩色影像，图7由扩散几何坐标（φ5，φ6，φ7）所构成的RGB彩色影像。

图6 由扩散几何坐标（φ2，φ3，φ4）所构成的RGB彩色影像

实验表明，基于局部线性重构的扩散坐标延拓算法能快速地计算出全景高光谱影像的扩散几何坐标，解决了扩散几何坐标难以处理海量规模的全景高光谱影像问题。然而，与我们之前基于坐标系配准的方法对比［13］，发现同样是由扩散几何坐标（φ5，φ6，φ7）构成的 RGB彩色影像，表示效果却大相径庭，造成这样结果的原因是扩散几何坐标的计算本质上是数据驱动（Data－driven）的，在构造扩散映射时选择不同的数据点就会产生不同的扩散几何坐标。因此，从实际应用角度而言，更倾向于本文所提出的基于局部线性重构的扩散坐标系延拓算法。因为算法3构造的基础是经过精心选择的Backbone，一旦Backbone确定，那么所延拓的扩散坐标系也能够保持一致，在实际应用中就可以依据Backbone的扩散坐标系对原有的基于线性的高光谱分析方法做相应的改进。同时，算法3本质上是流形半监督学习的一个特例，随着机器学习领域流形半监督学习方法的不断完善，对于海量高光谱影像能够得出更为精确的扩散几何坐标。

图7 由扩散几何坐标（φ5，φ6，φ7）所构成的RGB彩色影像

5 结语

直接用扩散几何坐标表示全景高光谱影像存在计算不可行的困难，由于全景高光谱影像通常达到计算机系统难以直接处理的庞大规模，使得构造扩散映射的几个关键步骤难以进行。本文通过借鉴局部线性嵌入LLE算法［15］的思想，设计了局部线性重构算法，并将该算法应用于全景高光谱影像扩散坐标表示算法。

从应用价值而言，全景高光谱影像利用扩散几何坐标进行表示，能够有效地发现某一地区环境的物种分布情况，对于实施大范围的环境监测具有重要的意义。如果能够得到某一地区充分多的高光谱影像，利用ε－net随机采样就能够得到该地区准确的Backbone，进而就可以将此Backbone的扩散几何坐标作为该地区各个物种的“指纹”特征，将对日后的应用带来极大的便利。

［1］Bellman R E.Dynamic Programming［M］.New Jersey：Princeton University Press，1957.

［2］Jolliffe T.Principal Components Analysis［M］.Berlin：Springer，1986.

［3］Cox T F，Cox M A A.Multidimensional Scaling［M］.London：Chapman and Hall，2001.

［4］Goodin D G，Gao J C，Henebry G M.The effect of solar illumination angle and sensor view angle on observed patterns of spatial structure in tallgrass prairie［J］.IEEE Transactions on Geoscience and Remote Sensing，2004，42（1）：154－65.

［5］Sandmeier S R，Middleton E M，Deering D W，et al.The potential of hyperspectral bidirectional reflectance distribution function data for grass canopy characterization［J］.Journal of Geophysical Research－Atmospheres，1999，104（D8）：9547－9560.

［6］Keshava N，Mustard J F.Spectral unmixing［J］.IEEE Signal Processing Magazine，2002，19（1）：44－57.

［7］Bachmann C M，Ainsworth T L，Fusina R A.Modeling data manifold geometry in hyperspectral imagery［C］／／IGARSS 2004：IEEE International Geoscience and Remote Sensing Symposium Proceedings，Vols 1－7－Science for Society：Exploring and Managing a Changing Planet，2004：3203－3206.

［8］Bachmann C M，Ainsworth T L，Fusina R A.Exploiting manifold geometry in hyperspectral imagery［J］.IEEE Transactions on Geoscience and Remote Sensing，2005，43（3）：441－454.

［9］Bachmann C M，Ainsworth T L，Fusina R A.Im－proved manifold coordinate representations of hyperspectral imagery［C］／／Proceedings of the IGARSS 2005：IEEE International Geoscience and Remote Sensing Symposium，Vols 1－8，Proceedings，2005：4307－4310.

［10］Bachmann C M，Ainsworth T L，Fusina R A，et al.Bathymetric Retrieval From Hyperspectral Imagery Using Manifold Coordinate Representations［J］.IEEE Transactions on Geoscience and Remote Sensing，2009，47（3）：884－897.

［11］Coifmfman R R，Lafon S，Lee A B，et al.Geometric diffusions as a tool for harmonic analysis and structure definition of data：Diffusion maps［J］.Proceedings of the National Academy of Sciences of the United States of America，2005，102（21）：7426－7431.

［12］Coifman R R，Lafon S.Diffusion maps［J］.Applied and Computational Harmonic Analysis，2006，21（1）：5－30.

［13］HE J，Zhang L，WANG Q，et al.Using Diffusion Geometric Coordinates for Hyperspectral Imagery Representation［J］.IEEE Geoscience and Remote Sensing Letters，2009，6（4）：767－771.

［14］何军.空间数据低维几何表示及其应用研究［D］.南京：东南大学仪器科学与工程学院，2009.

［15］Roweis S T，Saul L K.Nonlinear dimensionality reduction by locally linear embedding［J］.Science，2000，290（5500）：2323－2325.