基于知识表征的数学综合题教学实践与思考

刘海涛

众所周知，数学教学离不开解题教学，在安德森对知识的分类中，解题属程序性知识。综合题主要考查学生初中阶段所学的核心基本知识、基本技能以及综合运用所学知识分析问题和解决问题的能力。题目灵活多变，对学生的数学能力要求比较高，学生要综合运用所学的知识，还要运用数形结合思想、转化思想、函数思想、方程思想、分类讨论思想等常用的数学思想方法。综合题因解法多维，故属复杂性操作技能，因此，学生对综合题的表征不可能达到自动化的程度，是教学中的难点。如何表征，才能形成对综合题比较科学合理的数学认知结构，从而提高学生解答综合性问题的能力，本文就此谈谈笔者的实践与思考。

一、 “图形”基本化

图形基本化是指在复杂图形中分离出解题所需要的基本图形，利用基本图形的性质分析问题解决问题。数学是研究现实世界空间形式与数量关系的科学，空间形式具有复杂性，但很多复杂的图形是由基本图形组合而成，运用基本图形去研究复杂图形，把复杂图形的问题转化为基本图形的问题解决，是人类智慧的结晶。因此，基本图形的性质以及如何从复杂图形中分离出基本图形，是学生心须进行重点表征的。初中几何知识中，有很多基本图形，如相似形中的A型图、8型图、一线三等角、子母三角形等，这些基本图形的识别与依据其性质灵活运用是学生解决复杂问题思维载体。学生对这此基本图形的运用要达到自动化程度，也就是要形成简单操作性技能 （达到自动化），在解答问题时，把复杂图形转化为基本图形来解决，从而提高解答问题的能力。

例1：如图1，⊙O的半径为6，线段AB与⊙O相交于点C、D，AC=4，∠BOD=∠A，OB与⊙O相交于点E，设OA=x， CD=y．

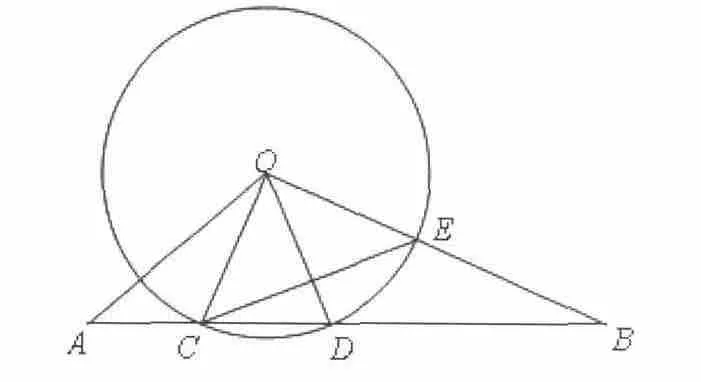
图1

（1） 求BD长；

（2）求y关于x的函数解析式，并写出定义域；

（3）当CE⊥OD时，求AO的长．

分析；此题由已知条件图形化之后，不难发现第 （1）问运用△ACO∽△ODB从而求出BD长。第 （2）问以第 （1）问为线索，从图形中分离出来子母三角形△ACO∽△AOB（如图2），可顺利解答此问。第 （3）问显然要把问题转化为方程问题。

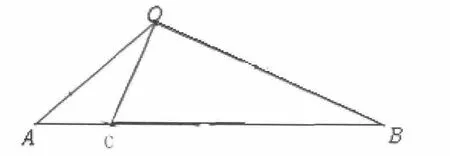
图2

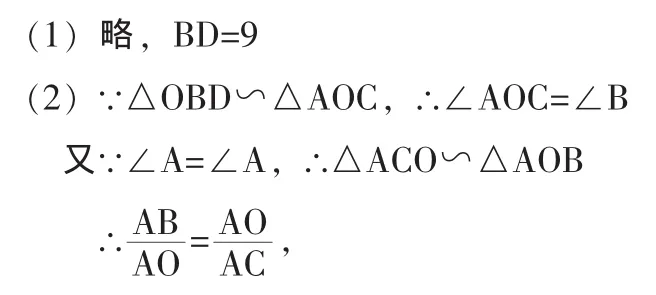
思考：基本图形的形状性质是教学中的重中之重，学生的数学认知结构中必须有基本图形清晰的表象，才能够与新的图形剌激产生联结，从而激活已经有的知识链，分离出基本图形。解题时，一是通过已知条件获得解题线索。此例中把已知条件图形化后，很快会发现相似的图形。二是通过敏锐的观察能力与表征的基本图形联结获得解题线索。此例中有几对子母三角形，那么在解题中运用哪一对呢？通过分析已知与未知所要的关系式，不难发现是运用△ACO∽△AOB这个线索。

二、 “动态”静态化

动态静态化是指把动态问题通过动态不变性法转化为静态问题来解决。动态问题是近几年的热点问题，动态问题反映的是现实世界的空间形式与数量关系的变化规律，此类题目往往以动点问题出现，动点问题是指以几何图形为背景的图形中存在一个或多个动点，它们在线段、射线、直线或弧线上运动，与其他定点构成特殊图形的一类开放性题目。此类题目灵活多变，动中有静，静中有动，动静结合，惟妙惟肖，动点运动的图形中存在动态不变性，学生只有发现问题中的这个规律，巧妙利用这个规律，综合运用初中阶段所学习的主要知识，才能解决问题。图形的动态不变性，是初中几何学重点研究的问题，例如：不论什么类型的三角形，内角和为180°，这就是一个动态不变的性质。但是对不同的题目其动态不变性是不同的，因此学生在表征此类题目时，可把动态不变性进行分类表征，如：角度不变性，相似不变性等。

例2：如图2，已知扇形AOB中，∠AOB=90°，OA=OB=2，C为弧AB上的动点，且不与A、B重合，OE⊥AC于E，OD⊥BC于D。

①若BC=1，求OD的长；

②在△DOE中，是否存在长度保持不变的边，若存在，求出该边的长；若不存在，请说明理由；

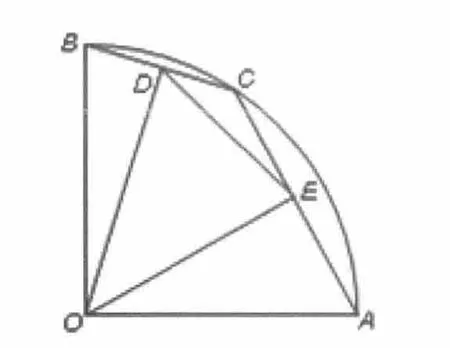
图3

③设BD=x，△DOE的面积为y，求y与x的函数关系式及定义域.

分析：如图4，本题第①问学生可顺利解答。第②问对部分学生来说有一定困难，原因是学生观察图形的能力以及对图形的感悟不理想，从中分析不出来点C在运动变化过程中，点D与点E始终分别是弦BC与AC的中点这个动态不变性，因此未能获得解题线索，不能顺利解答此问。事实上，如果分析出这个动态不变性，联结AB即可得线段DE的长度是不变的，始终是线段AB的一半。第③问要求△DOE的面积为y，依据三角形面积公式，必须知道一边及这边上的高，从已知不难发现OD是可用含x代数式来表示出来的，就是在△DOE中，知道了一条边，根据解三角形知识，可知还少一个角，如果再知道一个角，问题即可解决，通过观察图形不难发现联结OC可得∠DOE在点C的运动过程中，其度数是不变的，始终是45°，抓住这个动态不变性，通过添加辅助线DF⊥OE，利用解直角三角形知识，可顺利解答此题。

（2） 略， DE=2

（3）如图4，连结OC，作DF⊥OE交OE于点F

因为OD⊥BC，OE⊥AC，所以∠1=∠2，∠3=∠4又因为∠AOB=90°，所以

即∠DOE=45°又因为DF⊥OE，所以∠OFD=90°

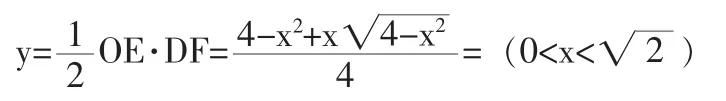
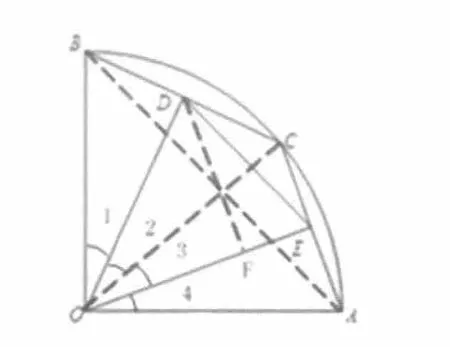
图4

思考：在解答此类试题时，一定要详细观察图形，分析出在动点变化过程中的图形不变性质，以此为线索运用所学的基本知识；另外，在教学中，要培学生对图形的观察能力，使学生善于从动态变化的图形中通过分类、比较、辨析、探索出图形的动态不变性质；最后，要使学生所学的知识能够形成一个稳定的认识结构，提高学生发散思维的变通性。

三、 “典型”对象化

典形对象化是指对非常典型的问题，以对象的形式进行表征。对象的三大特性是封装、继承、多态，一个对象解决一类问题。布鲁纳认为： “学习就是类目及其编码系统的形成。一个类目指一组有关的对象或事件，它可以是一个概念，也可以是一条规则。”〔1〕对象由问题及问题的解决方法组成，封装是指把问题与解决问题的方法表征放在一起，组成一个关联的整体，也即类目。继承是指把问题的已知条件进行等价变形，形成问题域，继承原问题的解决方法。多态是指进行一题多解、一题多变、一题多联。

首先，数学教学中有很多非常典型的例题，是一类题目的突出代表，学生解答此类题能用典型题这一把 “钥匙”开一类 “锁”，以达到 “做一题，通一类，会一片”的效果。

其次，问题与解决方法封装在一起有利于知识的提取。学生解题时，需从长时记忆中提取信息，当检索到所需要的知识信息时，因为问题与解决问题的方法进行了封装，因此可形成组块被提取到工作记忆中，有利于运用此知识信息进行新的信息加工。而对问题的的条件进行等价变式，有利于扩大问题的类比入口，从而在类比运用时容易被检索到。在解新题中，运用类比迁移进行解题，是解题教学中的重要思想方法。当对题目条件进行充分变式后，就能够扩大题目的类比范围，从而提高典型问题的类比率。还有，对问题进行一题多解、一题多变、一题多联有利于培养学生的发散性思维能力。发散性思维能力是创新思维能力的核心，一题多解可打开学生的解决问题的思路，使学生从多角度、多背景、多侧面去理解问题。一题多变可扩大问题本身的作用范围，同时培养学生的应变能力，深化解题思维，总结解题规律，培养创新思维能力，达到举一反三、触类旁通的目的。一题多联可形成问题系，丰富问题的CPFS结构。

例3：如图5，在直角坐标系中，O为原点．点A在x轴的正半轴上，点B在y轴的正半轴上，tan∠OAB=2，二次函数y=x2+mx+2的图象经过点A，B，顶点为D。

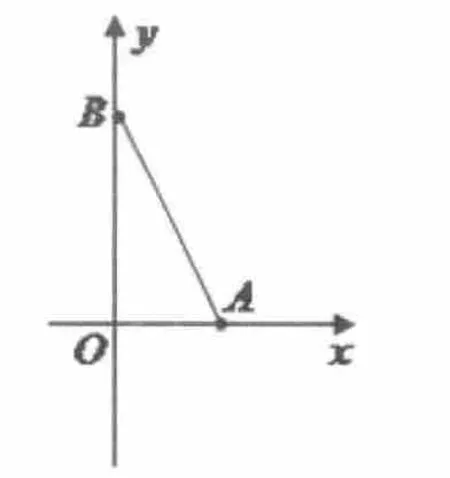
图5

（1）求这个二次函数的解析式；

（2）将△OAB绕点A顺时针旋转90°后，点B落到点C的位置．将上述二次函数图象沿y轴向上或向下平移后经过点C．请直接写出点C的坐标和平移后所得图象的函数解析式；

（3）设 （2）中平移后所得二次函数图象与y轴的交点为B1，顶点为D1．点P在平移后的二次函数图象上，且满足△PBB1的面积是△PDD1面积的倍，求点P的坐标．

分析： （1）二次函数y=x2+mx+2的图象经过点B，易得B点坐标为 （0，2）， 再由tan∠OAB=2求出A点坐标， 将二点坐标代入解析式即可求得函数解析式。

（2）易得C点坐标，由于沿y轴平移图象，故图象开口大小、对称轴均不变，设出解析式，代入C点作标即可求解。

（3）由于P点位置不固定，由图6可知要分①当点P在对称轴的右侧时，②当点P在对称轴的左侧，同时在y轴的右侧时，③当点P在y轴的左侧时，三种情况讨论。

解：略。

此题是比较典型的二次函数与几何图形面积相结合的综合性问题，第一，对问题可寻求多种解法。第二，对求二次函数解析式问题，可对条件进行充分的变式，例如：可给出AB=5，OB=2等。第三，可将此题与其它二次函数问题进行联系，形成问题系，如例4等。

例4：已知：如图，抛物线y=-x2+bx+c与x轴的负半轴相交于点A，与y轴相交于点B （0，3），且∠OAB的余切值为

（1）求该抛物线的表达式，并写出顶点D的坐标；

（2）设该抛物线的对称轴为直线l，点B关于直线l的对称点为C，BC与直线l相交于点E．点P在直线l上，如果点D是△PBC的重心，求点P的坐标；

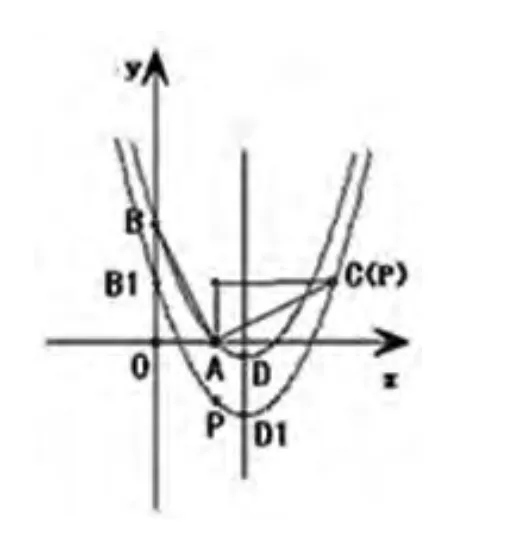
图6

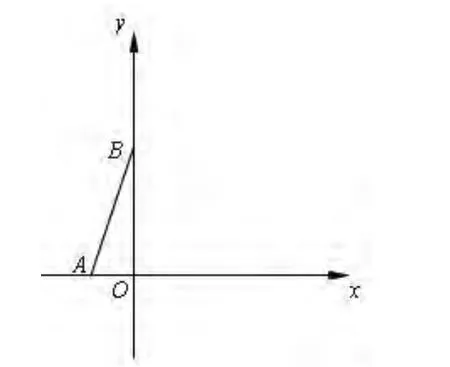
图7

（3） 在 （2） 的条件下， 将 （1） 所求得的抛物线沿y轴向上或向下平移后顶点为点P，写出平移后抛物线的表达式.点M在平移后的抛物线上，且△MPD的面积等于△BPD的面积的2倍，求点M的坐标.

思考：此题是典型的数形结合问题，学生在解答此题时，顺利画出图形是获取解题思路的重要步骤。函数问题是数形结合的精典范例，在解题过程中，运用数形结合思想，从图形中，才能获得解题线索。教学实践表明，如果题目本身有图，学生解答起来比较容易解答，如果题目没有图形，需学生自己画图，就增加了题目的难度，因此教学中要注重培养学生的画图能力，从而运用几何直观理解数学，使综合数学问题变得简明、形象，使抽象的数学问题形象化，才能提高学生解题的能力。学生对这类问题对象化后，会在长时记忆中形成此对象的清晰表征，便于需要时提取，同时对此类问题经变式训练可达到自动化程度。

四、 “局部”过程化

局部过程化是指对综合题的局部解题方法进行过程化，使学生对这些过程的表征形成简单操作技能。综合题虽然复杂多变，但在解题的过程中，还是由很多的逻辑段组成的，而这些逻辑段在很多题目中是出现过的，简言之综合题也是由简单的问题组合而成的。因此把这些动态不变的逻辑段程序化，形成简单操作技能供解题需要时提取，从而提高学生解题的能力。

例5：如图8，在平面直角坐标系XOY中，顶点为M的抛物线y=ax2+bx(a＞0)经过点A和x轴正半轴上的点B，AO=BO=2， ∠AOM=120°。

（1）求这条抛物线的表达式；

（2）联结OM，求∠AOM的大小；

（3）如果点C在x轴上，且△ABC与△AOM相似，求点C的坐标.

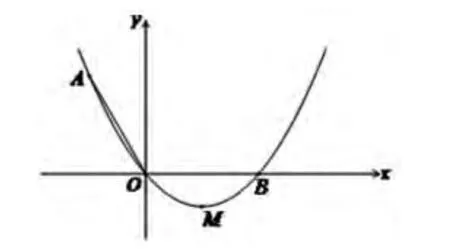
图8

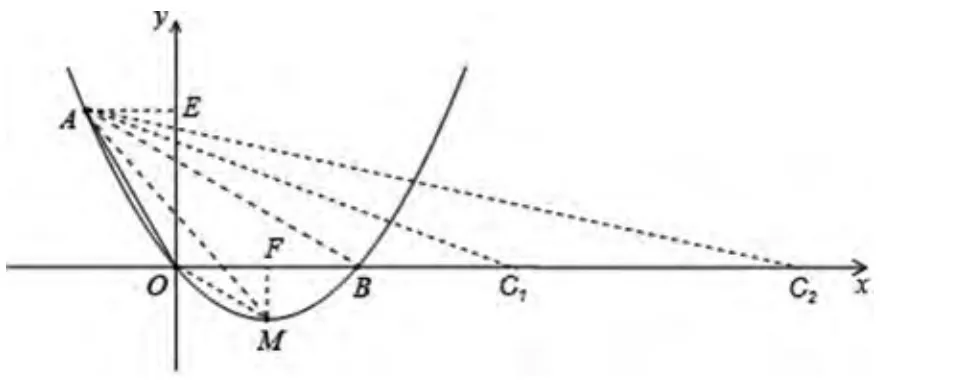
图9

分析：如图9，此题的第 （3）问，点C是X轴上动点，且△ABC与△AOM相似，此类问题是初三数学教学中的一个非常常见的一个问题，二个三角形相似分类讨论问题。此题二个三角形相似需两个条件，而题目中，隐含给一个角相等，∠ABX=∠AOM，而且题目分步引导学生先找到这对角相等，夹角两边对应成比例，然后分类讨论解答此题。

解： （1） 过程略

综上所述，△ABC与△AOM相似时，点C的坐标为：（4， 0） 或 （8， 0） ．

思考：综合题灵活多变，解题不能形成一个自动化的程序，但是，初中数学中的一些基本问题，其变化是有一定的规律性，且在综合题中经常出现，因此，这些问题虽属程序性知识，但因解题的思维过程比较固定，因此表征时可形成一个简单的操作技能，待需要时可快速提取运用于解决问题的过程中。

总之，综合题的解答对学生来说是一个难点，虽然每个学生用自己的习惯表征不同的数学知识信息，但教学中，教师可通过显现知识不同方式及教学策略，改变学生的知识表征策略，指导学生科学合理的对综合题的教学进行合理表征，这样才能优化学生的数学认知结构；才能提高学生的思维品质；才能提高学生的综合分析问题、解决问题的能力。

①孔凡哲，曾峥著.数学学习心理学 〔M〕.北京：北京大学出版社， 2009 （3）： 43.

②张学民.实验心理学 〔M〕.北京：北京师范大学出版社2009（8）： 583.