环境约束下长江流域主要城市全要素生产率研究

张建升

（重庆三峡学院 经济与管理学院，重庆 404120）

一、引言

长江流域地处整个中国版图的腰腹地带，涵盖了川、湘、鄂、赣、皖、苏、沪等10 省市，流域面积占全国18%、人口占全国36%、GDP 占全国37%。自20 世纪90年代开始，长江流域先后开发并形成了以重庆和成都为中心的长江上游城市群经济连绵带、以武汉为中心的中游城市群经济连绵带、以上海和南京为中心的长江下游城市群经济连绵带，这三大城市群经济带已成为全国工业生产和服务业最为密集的地区之一，长江流域经济带被誉为继中国沿海经济带之后最有活力的经济带。然而，在经济社会快速发展的同时，长江流域也同样面临环境污染严重、水质不断下降的困扰，入河污染物逐年增加，长江流域废污水排放量在20 世纪70年代末为95 亿t/a，80年代末尾150t/a，90年代末超过200t/a，到2011年已达到342.1t/a，年均递增速度约为3%。长江流域工业废水排放量2001年为138.3亿吨，到2011年激增为227.3亿吨[1]。长江流域经济的快速发展同样面临着环境的刚性约束。

如何在实现经济快速发展的同时减少环境污染成为长江流域可持续发展的关键问题。而实证考察环境与经济之间关系的一种重要思路是探讨考虑环境污染时的全要素生产率的变化。全要素生产率是在生产过程中利用全部投入要素获得产出的能力水平的重要度量指标，最早由索洛（1957）提出，也称为“索洛余值”，目前已经在农业、制造业、服务业以及区域经济比较等领域广泛应用（刘秉镰，李清彬，2009[2]；李希义，2013[3]；辛玉红、李星星，2014[4]），是经济增长问题最为流行的研究领域之一。但长期以来对传统全要素生产率的测算仅仅考虑了合意产出（GDP），并没有考虑非合意产出（例如碳排放量、工业废水等）对环境的影响，实际上是忽略了经济增长对社会福利的负面影响，无法反映出经济增长的真实绩效。传统全要素生产率的测度主要通过Malmquist 指数，但该指数无法解决非合意产出问题，Chung et al（1999）[5]在测度瑞典纸浆厂的全要素生产率时，引入方向性距离函数（Directional Distance Function）， 并对Malmquist 指数进行修正，修正后的Malmquist 指数也被称为Malmquist-Luenberger 指数（以下简称ML 指数），这个指数可以测度存在环境约束时的全要素生产率。近年来，国内一些学者已经采用ML 指数对考虑环境因素的全要素生产率进行实证研究（王兵、吴延瑞等，2010[6]；田银华、贺胜兵等，2011[7]；李静、陈武，2013[8]）。

在对城市全要素生产率的研究方面，也产生了一些比较有代表性的成果：戴永安（2010）从人口、经济和社会角度研究了中国的城市化效率，考察了其时空演变和影响因素，并对中国城市化的全要素生产率做了动态分析和区域比较，结果表明城市化效率缓慢增长，城市间效率差异显著，但效率差距是逐渐缩小的，在影响因素方面，城市的初始状态、区位、空间集聚水平、产业结构效益与基础设施水平对各城市化效率存在显著的正向作用，人口因素和政府的作用却限制了城市化效率的提高[9]。邵军、徐康宁（2010）基于Malmquist指数分析方法，测度了我国城市的生产率增长、效率改进与技术进步。研究表明自20 世纪90年代末期以来，我国城市生产率的增长率持续下降，并连续多年出现负值，导致生产率水平下降，而这主要是由技术水平下降所致，但城市效率水平同期却有了较为明显的改进[10]。管驰明、李春（2013）运用索洛残差法对上海市1979-2011年的全要素生产率进行了估算，并对其增长源泉进行定量分析，结论表明全要素生产率对上海经济增长发挥着日益重要的作用[11]。

从以上文献可以看出，虽然关于我国城市全要素生产率的研究已经较为丰富，但都没有考虑环境因素的影响，基于此，本课题试图在考虑环境因素的前提下，基于“绿色生产率”的视角，以我国长江流域沿线主要城市的投入产出数据为基础，测算并比较在考虑环境因素和未考虑环境因素两种情形下的全要素生产率，进而合理评价长江流域主要城市的经济发展绩效。

二、模型与方法

（一）环境生产技术的数学表达

区域经济发展过程中，在实现“好”产出增加的同时，不可避免地要产生一些副产品，比如废水、废气等，称之为“坏”产出或者“非合意”产出。为实现资源、环境与经济的协调发展，需要将资源与环境等要素纳入生产函数中，构建既包括诸如GDP等“好”产出又包括环境污染等“坏”产出的生产可能性集，即环境技术。假设一个城市为一个决策单元，各个城市使用N中投入X=(x1,x2,…,xN）∈RN+，生产了M种“好”产出Y=(y1,y2,…,yN）∈RM+，同时也生产了I 种“坏”产出U=(u1,u2,…,uN）∈RI+，则环境技术的生产可能性集为：

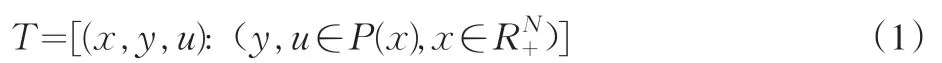
生产可能性集p(x)是一个有界的闭集，具有以下特性：

（1）“好”产出与“坏”产出的联合弱可处置性（Jointly Weak Disposability）。如 果(y,u)∈p(x) ，且0 ≤θ≤1 ，则(θy,θu)∈p(x)，表明在既定投入水平下，当“坏”产出减少时，“好”产出也要相应的减少。

（2）投入与“好”产出的强可处置性（Strong or Free Disposability）。如果x′≤x，则p(x′)⊆p(x) ；如果(y,u)∈p(x) 且y′≤y，则(y′,u)∈p(x)。意味着“好”产出可以自由支配，但“坏”产出却保持不变

（3）“好”产出与“坏”产出的零结合性（Null-Jointness）。如果(y,u)∈p(x)，且b=0，那么y=0。表明在产生“好”产出的同时，不可避免的产生“坏”产出。根据Fare et al等学者的研究，p(x)满足零结合性，还需满足以下两个条件：

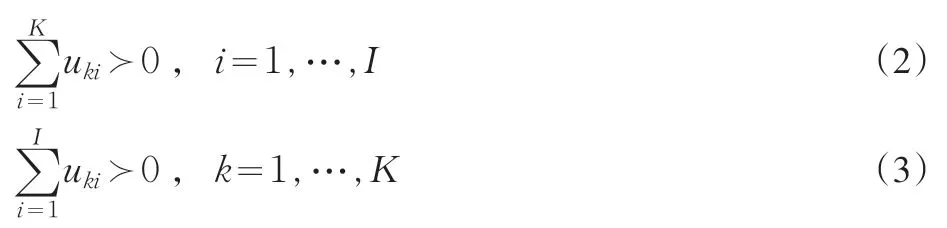
式（2）表示至少一个生产单位在生产一种“坏”产出；式（3）表示每一个生产单位至少生产一种“坏”产出。

（二）方向性距离函数

为实现区域经济增长过程中，“好”产出增加“坏”产出减少的目的，本文引入方向性距离函数来表示[12]。方向性距离函数表示既定方向g=(gy,-gb)、投入x和生产可能性集p(x)下，“好”产出保持一定比例增加的同时，“坏”产出同比例减少的可能性。定义为：

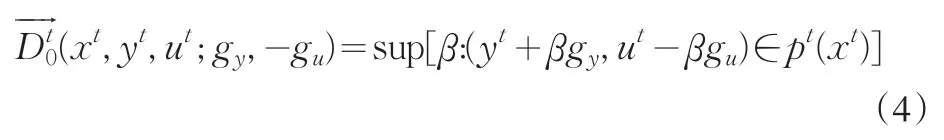
（4）式是t时期内的方向距离函数，比较的是(yt,ut)和t期的生产前沿，即每一产出在当期的方向距离函数，g=(gy,-gu)为方向向量。而事实上，Shephard的产出距离函数是方向距离函数的一种特殊情况，两种距离函数的关系可以表示为：

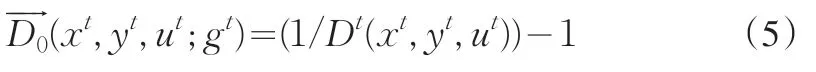
如果将“好”产出与“坏”产出同等对待，要求两者按相同比例增加或减少，此时的方向向量是中性的g=(y,-u)。生产单位在t时期的方向性距离函数可通过数据包络分析转化为线性规划求解：

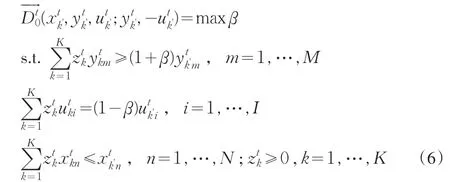
（三）Malmquist-Luenberger（ML）生产率指数

在方向性距离函数基础上，根据Chung et al.的研究，基于产出的从t 时期到t+1 时期的ML 生产率指数可通过四个方向性距离函数的求解得出：

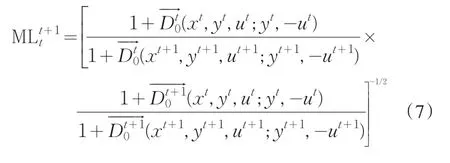
如果ML指数大于1，表明从t时期到t+1时期的生产率是增长的，反之则下降。

进一步将ML指数分解为效率变化指数（MLEFFCH）和技术进步指数（MLTECH）:

如果效率变化指数MLEFFCH大于1，表明决策单元在向生产前沿面靠近，效率得到提升，反之则说明决策单元在远离生产前沿面。技术进步指数MLTECH大于1 说明决策单元生产技术进步，反之则表明技术退步。

三、变量选取与数据说明

（一）数据说明

由于工业废水统计口径的限制，本文采用2003-2012年中国长江流域沿岸24个地级市的投入产出数据。为便于比较分析，本文根据地理位置将以上各个地级市划分为长江上游、中游和下游三大地区，长江上游地区包括重庆市和四川省内的地级市；长江中游地区包括了湖北、湖南、江西、安徽所辖长江沿岸城市；江苏省内城市及上海市划归到长江下游地区。相关数据均来源于《中国城市统计年鉴》、《中国统计年鉴》。样本观测值的统计描述如表1所示。

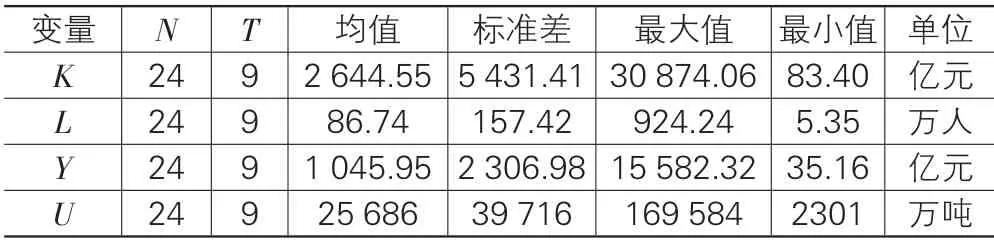
表1 变量的描述性统计

（二）投入产出指标选择

投入指标：选择资本存量和劳动力作为投入指标。劳动力（万人）是以各城市“年末单位从业人员数”和“城镇私营和个体从业人员”数据加总而得。资本存量（万元）采用“永续盘存法”进行计算，计算公式为：Kit=Kit-1(1-δ)+Iit/Pit，δ为折旧率，采用张军等（2004）[13]学者的研究结果，取值为9.6%。基年资本存量借鉴Young(2000)[14]的方法，以2000年固定资产投资总额除以10%作为初始资本存量。由于现行统计中没有关于各城市固定资产投资价格指数的数据，因此，为剔除价格因素的影响，计算结果采用各城市所属省份的固定资产投资价格指数折算为2000年不变价。

产出指标：包括“好”产出和“坏”产出。“好”产出为各城市GDP，以其所在省份GDP 平减指数折算为2000年不变价。对于“坏”产出，目前常用的指标包括二氧化碳、二氧化硫、化学需氧量、废水排放量等，考虑到废水对长江污染的危害更为严重，同时囿于数据的可获取性，本文采用“废水排放量”作为“坏”产出。对于废水排放总量的计算，以市辖区工业废水排放量和城镇居民生活污水排放总量加总表示。其中，对于工业废水排放量由于目前仅统计了全市口径的工业废水排放量，未统计市辖区工业废水排放量，故本文采用市辖区限额以上工业总产值占比乘以全市工业废水排放量来近似市辖区工业废水排放量。城镇居民生活污水排放总量的计算根据环境科学部华南环境科学研究所的方法，计算公式为：G=365×NcF×10，其中G表示城镇生活源水污染物年产生量（吨/年），Nc表示市辖区城镇常住人口（万人），在计算中以年末总人口数代替，F 表示城镇居民生活污水产生系数（升/人·天），各城市居民生活污水产生系数值同样采用环境科学部华南环境科学研究所的计算结果。

四、结果分析

（一）考虑非期望产出的生产前沿与投入产出效率

表2 显示了在考虑非期望产出的情况下，长江流域主要城市2003-2012年投入产出效率的平均值及变动情况。

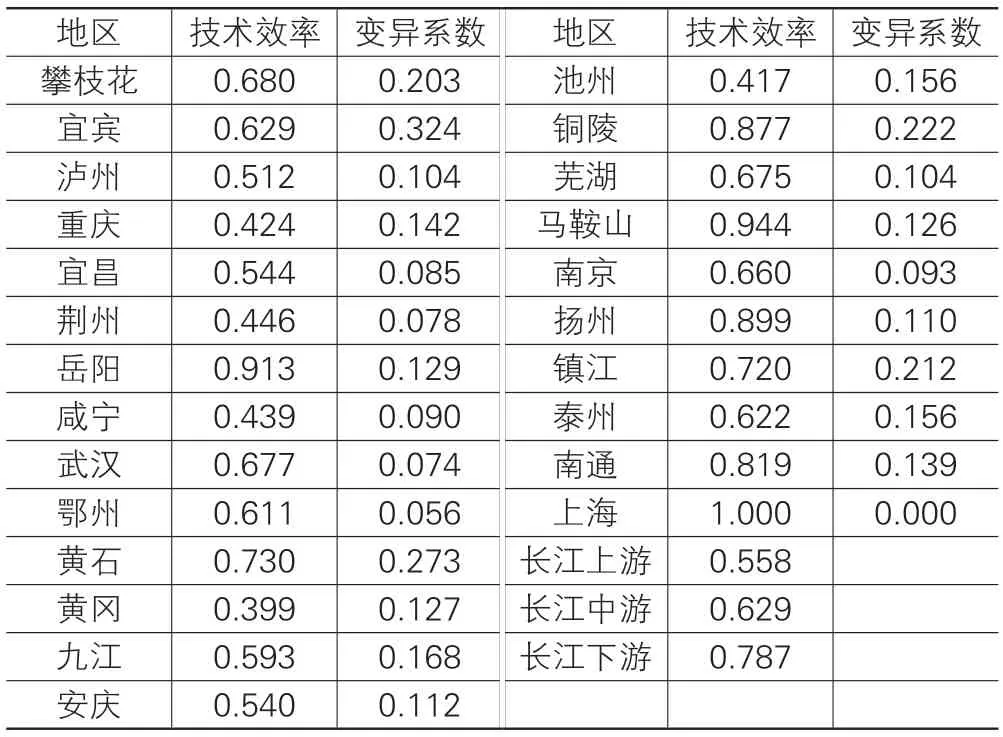
表2 各城市考虑非期望产出的技术效率值及变异系数

（1）长江流域各城市投入产出效率差异较大，但差异在逐渐缩小。样本期间，位于生产前沿上的城市数量最多的年份为2012年，有6 个城市；其次，在2003年和2009年分别有5 个位于生产前沿。总体数量占样本数量的比例仅为20%多，反映了技术无效率是长江流域主要城市的普遍现象。从10年的平均值来看，始终处于生产前沿面上的城市只有上海市，效率值最低的5 个城市分别为：黄冈（0.399）、池州（0.417）、重庆（0.424）、咸宁（0.439）、荆州（0.446），均为长江中上游城市；从各年份的变异系数值来看，各城市在2003年的变异系数值为0.322，而到2011年和2012年分别为0.293 和0.307，说明环境约束下的各城市技术效率值虽然差异较大，但这种差异在逐渐缩小。

（2）分区段来看，长江上、中、下游城市投入产出效率呈现从低到高的阶梯式分布。长江上游城市投入产出效率平均值为0.558，中游城市为0.629，下游城市均值为0.787，这一分布特征与中国东、中、西部地区的经济发展特征较为相似。

（3）长江流域各城市投入产出效率变化差异较大。为分析各城市在不同年份投入产出效率的变化情况，进一步计算了其变异系数，从结果来看，宜宾、黄石、铜陵、镇江和攀枝花5个城市变异系数最大，以宜宾市为例，在2011和2012年技术效率值均为1，处于生产前沿面上，而在其他年份中，最低的技术效率值仅为0.469，说明部分城市技术效率不稳定，变化差异大。

（二）两种情形下的全要素生产率及其分解

表3、表4分别显示了在不考虑环境因素和考虑环境因素两种情形下，长江流域主要城市全要素生产率随时间的动态演进趋势及各城市之间的差异。

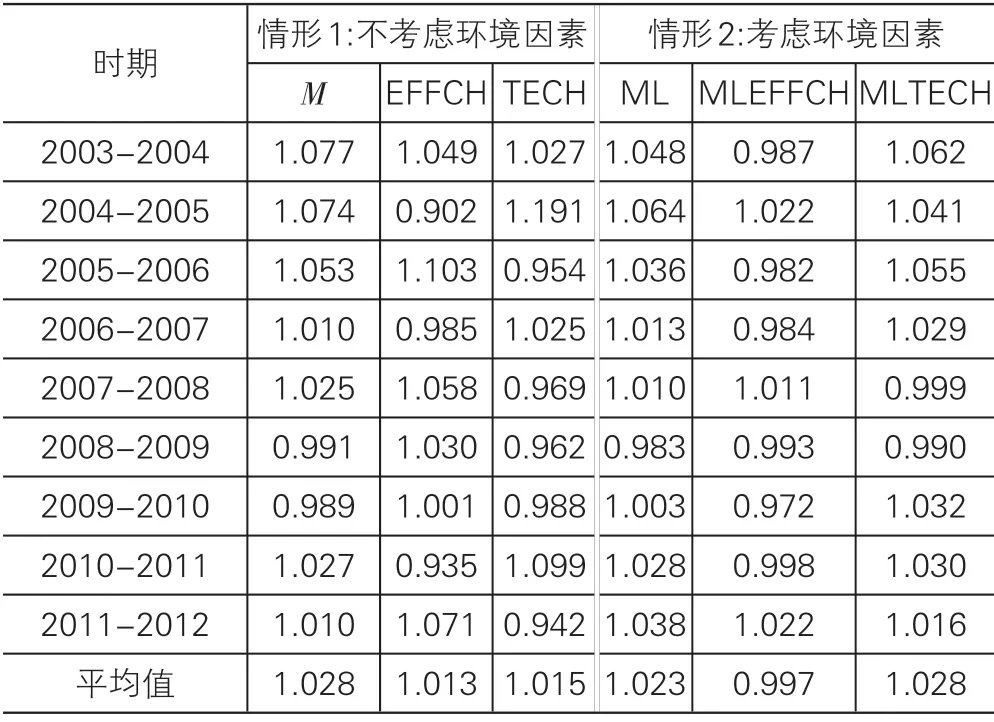
表3 两种情形下的全要素生产率及其分解：时间趋势

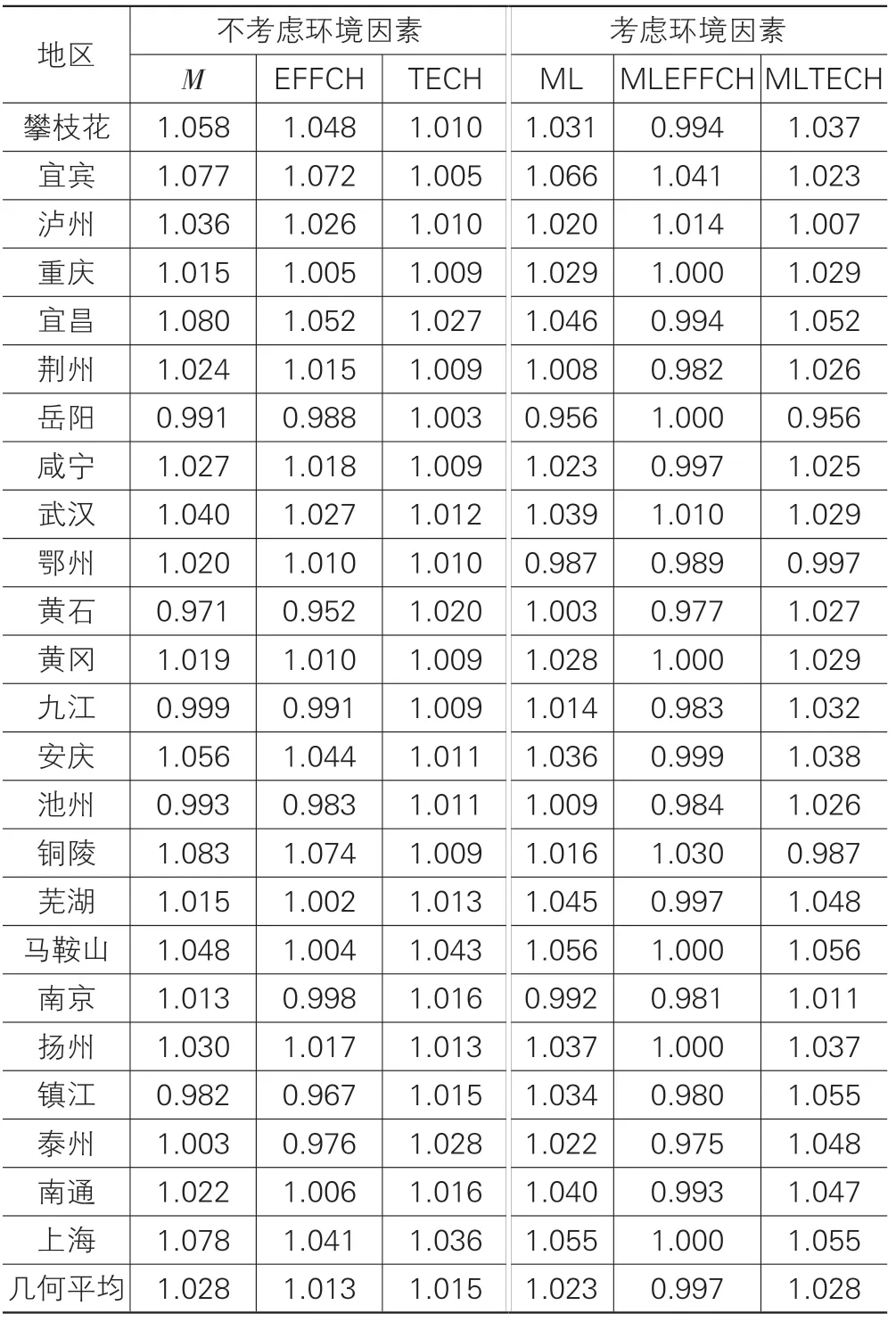
表4 两种情形下的全要素生产率及其分解:区域差异

从表3可以看出：

（1）当考虑环境因素时，长江流域城市全要素生产率出现明显下降。在不考虑环境因素的情况下，2003-2012年，长江流域城市全要素生产率年均增长2.8%，而当考虑环境因素时，全要素生产率年均增长率降低为2.3%，年均下降0.5个百分点，说明不考虑环境因素的TFP被高估。

（2）长江流域城市全要素生产率不断增长，技术进步是其增长的主要源泉。对不考虑环境因素的全要素生产率分解表明，技术进步率年均增长1.5%，效率改善值年均为1.3%，两者差距并不大；但当考虑环境因素时，技术进步率为2.8%，技术效率则出现了轻微的恶化，年均下降0.3%，这一结果表明，环境约束下长江流域城市全要素生产率的增长主要是技术进步的贡献，技术效率贡献值较小甚至为负影响。

（3）长江流域城市全要素生产率增长率整体呈现“V”字型演变。从图1 可以清晰地看出，从2003年开始，城市TFP整体呈现不断下降态势，ML指数2009年最低，TFP增长率为-1.7%；M指数2010年最低，TFP增长率为-0.9%；分析认为这可能是由于全球金融危机的影响所致，在金融危机过后，经济开始逐步恢复，到2011年全要素生产率增长分别为2.7%和2.8%，2012年分别为1.0%和3.8%。

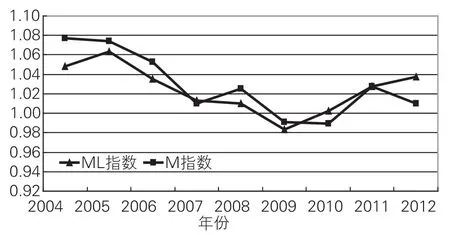
图1 不同年份两种情形下TFP值的变动情况

从表4可以看出，在样本期间：

（1）长江流域城市全要素生产率增长差异较大。从环境约束下的城市全要素生产率增长情况来看，长江流域24个城市中，只有鄂州、南京和岳阳3 个城市出现了全要素生产率的倒退，年均下降幅度分别为1.3%、0.8%和4.4%。年均增长排名前5 位的城市分别为：宜宾（6.6%）、马鞍山（5.6%）、上海（5.5%）、宜昌（4.6%）、芜湖（4.5%）。

（2）多数城市在技术进步快速提高的同时，技术效率明显恶化。在24个城市中，只有宜宾、泸州等4个城市技术效率得到改善，重庆、岳阳等6 个城市技术效率不变，其他城市技术效率都出现恶化，进一步说明了技术效率恶化是阻碍长江流域城市绿色全要素生产率提高的主要原因。

（3）环境约束对不同城市全要素生产率的影响差异较大。当考虑环境因素时，多数城市全要素生产率增幅出现明显下降，但下降幅度并不相同，增幅下降最大的城市为铜陵市，下降6.7%，其他下降较多的城市及下降幅度为：宜昌（3.4%）、岳阳（3.5%）、鄂州（3.3%）和攀枝花（2.7%）。

（4）分区段来看，不考虑环境因素时，长江上中下游城市全要素生产率年均增长分别为：4.6%、2.6%和2.1%；而考虑环境因素时，上中下游城市全要素生产率年均增长分别为3.6%、1.9%和3.0%。两种情形下长江上游城市全要素生产率都明显高于中下游城市，中下游城市TFP总体接近，说明近年来随着中西部地区经济的快速发展，长江上、中游城市经济也明显提速，东中西差异不断缩小。但两种情形下的比较可以看出，当考虑环境因素时，长江上游中游城市TFP增长幅度分别降低了1.0%和0.7%，说明这两个区段的城市在经济快速发展的同时，也产生了大量的污染。而长江下游城市的全要素生产率在考虑环境因素时，则由原来的2.1%提升为3.0%，说明了长江下游城市在城市的快速发展过程中，更加注重环境污染的治理和保护，将环境友好提升到了与经济发展同等重要的地位，实现环境与经济的良性互动发展。

（5）对两种情形下长江上中下游城市全要素生产率的分解结果对比表明，当忽略环境因素的影响时，均高估了技术效率改善对全要素生产率的贡献而低估了技术进步的贡献。当考虑环境因素时，长江中游地区城市技术效率由原来的年均增幅1.2%下降为衰退0.4%，技术进步则由1.4%提高到2.3%；长江下游地区城市技术效率由原来的年均增长0.1%下降为衰退1.2%，技术进步则由1.1%提高到4.2%；变动最明显的为长江上游地区，技术效率由年均增幅3.7%下降为1.2%，技术进步则由0.8%增长为2.4%。

五、结束语

本文采用方向性距离函数和ML 生产率指数对考虑非期望产出下的生产前沿与技术效率、以及考虑环境因素和不考虑环境因素两种情形下我国长江流域2003-2012年24个城市的全要素生产率进行了测度。主要得出以下几点结论：

（1）当考虑非期望产出时，只有上海市始终处于生产前沿面；技术无效率是长江流域主要城市的普遍现象，各城市之间投入产出效率差异大且不稳定；各城市变异系数值由2003年的0.322下降为2012年的0.307，说明环境约束下的各城市技术效率值虽然差异较大，但这种差异在逐渐缩小；分区段来看，长江上、中、下游城市技术效率呈现从低到高的阶梯式分布。

（2）从长江流域城市全要素生产率随时间的演变趋势来看，全要素生产率增长率从2003年开始整体为下降趋势，金融危机之后又开始不断提升；当考虑环境因素时，长江流域城市全要素生产率出现明显下降，说明不考虑环境因素的TFP被高估；长江流域城市全要素生产率不断增长，技术进步是其增长的主要源泉。

（3）从长江流域各城市全要素生产率之间的差异来看，多数城市在技术进步快速提高的同时，技术效率明显恶化，进一步说明了技术效率恶化是阻碍长江流域城市绿色全要素生产率提高的主要原因；环境约束下的城市全要素生产率增长差异大，只有鄂州、南京和岳阳3 个城市出现了全要素生产率的倒退，其他城市全要素生产率都不断增长；两种情形下长江上游城市全要素生产率都明显高于中下游城市，但当考虑环境因素时，长江上游、中游城市TFP增长幅度分别降低了1.0%和0.7%，说明这两个区段的城市在经济快速发展的同时，也产生了大量的污染；进一步的分解结果说明，忽略环境因素时技术效率改善值被明显高估，而技术进步对全要素生产率的贡献则被低估。

［1］周少林，饶和平，张兰.长江流域分行政区入河污染物总量监督管理探析［J］. 人民长江，2013，44（24）：1-5.

［2］刘秉镰，李清彬. 中国城市全要素生产率的动态实证分析：1990-2006［J］. 南开经济研究，2009（3）：139-152.

［3］李希义. 我国商业银行业的全要素生产率测算和增长因素分析［J］. 中央财经大学学报，2013（9）：19-25.

［4］辛玉红，李星星. 中国新能源上市公司全要素生产率动态变化实证研究［J］. 华东经济管理，2014，28（2）：49-52.

［5］Chung Y H，Fare R，Grosskopf S. Productivity and Undesirable Outputs：A Directional Distance Function Approach［J］.Journal of Environmental Management，1997，51：229-240.

［6］王兵，吴延瑞，颜鹏飞. 中国区域环境效率与环境全要素生产率增长［J］. 经济研究，2010（5）：95-109.

［7］田银华，贺胜兵，胡石其. 环境约束下地区全要素生产率增长的再估算：1998-2008［J］. 中国工业经济，2011（1）：47-57.

［8］李静，陈武. 中国工业的环境绩效与治理投资的规模报酬研究［J］. 华东经济管理，2013，27（3）：44-50.

［9］戴永安. 中国城市化效率及其影响因素［J］. 数量经济技术经济研究，2010（12）：103-118.

［10］邵军，徐康宁. 我国城市的生产率增长、效率改进与技术进步［J］. 数量经济技术经济研究，2010（1）：58-67.

［11］管驰明，李春. 全要素生产率对上海市经济增长贡献的实证研究［J］. 华东经济管理，2013，27（10）：7-10.

［12］李谷成，陈宁陆，闵锐. 环境规制条件下中国农业全要素生产率增长与分解［J］. 中国人口·资源与环境，2011，21（11）：153-159.

［13］张军，吴桂英，张吉鹏. 中国省际物质资本存量估算：1952-2000［J］. 经济研究，2004（10）：35-43.

［14］Young A. Gold into Base Metals: Productivity Growth in the People’s Republic of China during the Reform Period［R］. NBRE working paper，No. 7856，2000.