基于三次hermite插值lmd方法的往复压缩机故障诊断技术
2014-11-27陈桂娟邹龙庆贾春雨付海龙
陈桂娟,邹龙庆,贾春雨,付海龙
(1.东北石油大学机械科学与工程学院,黑龙江大庆163318;2.大庆石化公司,黑龙江 大庆163714)
1 引言
往复压缩机是石油化工企业广泛使用的增压设备,其具有激励源众多,部件运动形式多样等特点,其传动机构轴承常因加工装配误差或磨损出现间隙故障,致使整机状态劣化而停机。振动信号富含设备状态信息,是故障诊断技术实施的有效途径。往复压缩机振动信号具有如下特征:(1) 振动信号呈现强非平稳特性;(2) 因激励源众多,振动信号为多分量耦合信号。以傅立叶变换为基础的频域分析方法,难以对其振动信号进行准确的故障诊断[1]。
英国学者Smith,于2005年提出了一种全新的信号分解方法——局部均值分解(local mean de-composition,lmd)[2]。lmd方法对存在非线性、非平稳性的机械设备振动信号具有良好的分析能力,且避免了Hilbert变换产生的边缘效应及无物理意义的负频率等问题,现已在轴承等机械设备故障诊断领域得到广泛应用[3-4]。鉴于往复压缩机振动信号具有的非平稳性和多分量耦合特性,lmd是其振动信号的理想分析方法。
然而,lmd方法是以滑动平均法获得局部均值和包络估计的,该方法多次平滑后会产生相位差,导致分解结果失真[5]。三次hermite插值法是一种较为常用的插值曲线构造方法,以其构造局部均值与包络估计不仅能够避免滑动平均法存在问题,而且该方法仅要求节点一阶导数连续,具有优良的保形特性,尤其适合于具有强非平稳特性信号的分析。
本文针对往复压缩机振动信号的强烈非平稳特性,结合三次hermite插值法具有的优良保形特性,提出基于三次hermite插值的lmd方法,提高局部均值函数和包络估计函数的拟合精度,并以PF分量的包络幅值频谱作为依据,实现往复压缩机传动机构轴承间隙故障的准确诊断。
2 基于三次hermite插值的lmd方法
2.1 lmd方法原理
lmd分析方法实质是将时间序列分解为多个PF分量与残余分量之和,其中PF的瞬时幅值就是所对应的包络信号。对于任意时间序列x(t),其算法步骤如下:
(1)找出时间序列x(t)的全部极值点ni,利用公式(1)计算任意两相邻点的均值mi和包络值ai,再对二者分别以滑动平均法得到平滑的局部均值函数m11(t)和包络估计函数a11(t)。

(2)将局部均值函数m11(t)从原始时间序列x(t)中减去,即得h11(t)

(3)以包络估计函数a11(t)除h11(t),既得到s11(t)

再按照以上步骤求出s11(t)所对应的a12(t),若a12(t)与1之差值小于误差,则s11(t)为纯调频函数,若a12(t)与1之差值大于误差,则循环上述过程n次,直至s1n(t)所对应的a1(n+1)(t)与1之差值小于误差为止,也即s1n(t)为一个纯调频信号。
(4) 将循环过程中产生的所有包络估计函数相乘即得到第一个PF分量所对应的包络信号a1(t)
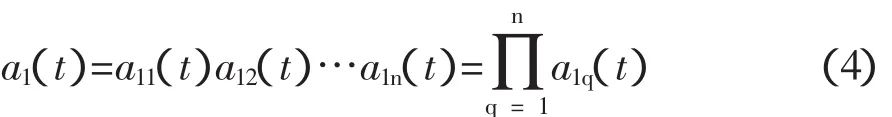
(5)将纯调频信号s1n(t)与包络信号a1(t)相乘即可得到第一个PF分量

(6)从原始时间序列x(t)中减去第一个分量PF1(t),便得到一个新的时间序列u1(t),将其作为原始序列重复以上过程,循环k次,直到uk单调为止。
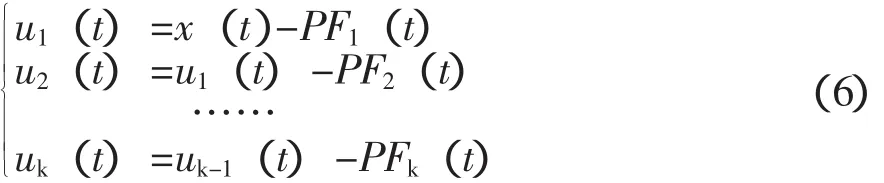
这样即将原始时间序列x(t)分解为k个乘积函数和一个残余分量,即

2.2 三次hermite插值
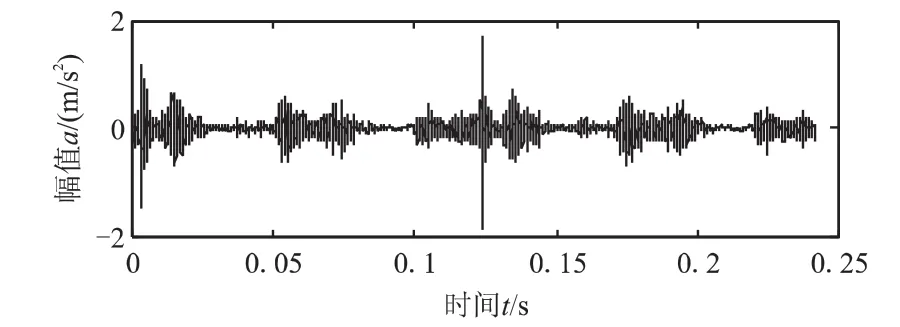
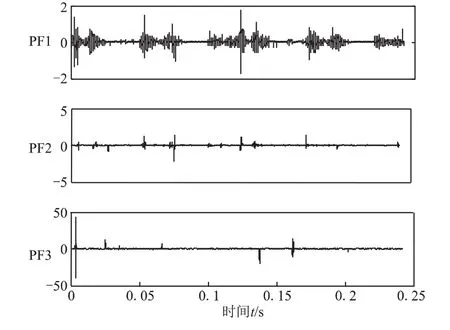
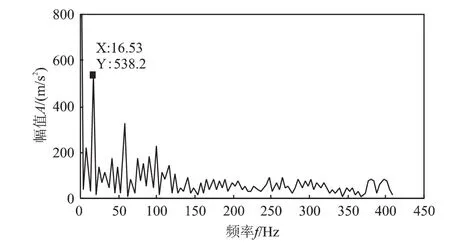
一般对于给定的节点a=x0 其中标准三次hermite的基函数具有如下形式 它们满足 且有Fi(t)+Fi+1(t)=1,Gi(t)=-Gi+1(1-t) 采用滑动平均方法存在多次平滑后误差较大的缺点,且往复压缩机振动信号具有强烈的非平稳性,结合三次hermite插值法的优良保形特性,本文提出以三次hermite插值方法替代滑动平均方法计算局部均值函数和局部包络函数过程,利用三次hermite插值分别对极大值点和极小值点插值求得上下包络线,再以其计算得出局部均值函数和局部包络函数的方法。具体步骤如下: (1)计算得出原始信号x(t)的极值点序列nk,对其进行端点延拓,得到新的极值点序列Xk; (2) 利用三次hermite插值法对极大值点进行插值,形成上包络函数Emax,同样利用三次hermite插值法对极小值点进行插值,形成下包络线Emin; (3) 利用下式即可计算得出局部均值函数m11(t)和局部包络函数a11(t) 得到局部均值函数和包络估计函数后,继续执行lmd的后续步骤即可以实现基于三次hermite插值的lmd分解方法。 以2D12型往复压缩机为研究对象,其主要参数为:轴功率500 kW、排气量70 m3/min、活塞行程240 mm、电机转速496 r/min。生产过程中,其常因连杆轴瓦间隙过大引起振动超标而停机,该故障的准确诊断可提高生产效率,降低维护成本。该压缩机传动机构的一级连杆上大头轴承正常径向间隙为0.1~0.22 mm。试验过程中,利用已磨损的轴瓦,在压缩机传动机构的一级连杆上模拟了大头轴承间隙大故障,其径向间隙为0.35 mm。根据压缩机结构特点,在一级十字头滑道下端利用加速度传感器测得振动信号,该测点振动信号时域波形与频谱分别如图1和图2所示。由图1可知,由于间隙过大,在时域波形中出现了明显的冲击信号,具有强非平稳特性。频谱中,峰值主要位于中高频,基频倍频处无明显峰值。 根据动力学理论可知,往复压缩机振动信号是以振动传递部件的固有频率为载波频率,以部件运动频率对其进行调制的调幅信号。由于运动形式多样、激励源众多,实测信号可以认为是由多个调幅信号耦合而成。因此,往复压缩机振动信号适合于应用lmd方法进行分解。 为验证本文方法的优越性,以传统lmd方法和本文提出的改进方法对往复压缩机故障信号进行分解。分解过程中以镜像延拓法降低端点效应,迭代终止条件的误差设置为10-3。由于分解结果中的前几个分量包含了设备状态的主要信息,所以仅给出了2种方法分解结果的前3个PF分量,分别如图3和图4所示。 如此前分析,往复压缩机振动信号是以内部部件运动频率作为振动信号调幅频率,因此,进一步对PF分量的瞬时幅值a(t)进行频谱分析,可得出内部运动部件的激励频率,判定设备运行状态。分别对传统lmd方法和本文lmd方法的第一个PF分量进行幅值频谱分析,频谱图如图5和图6所示。可以看出,2种方法的频谱均在2倍频处出现了最大峰值,这与轴承间隙过大故障中一次往复运动出现2次冲击的故障机理是一致的。因此,lmd方法可以有效诊断出往复压缩机轴承间隙过大的故障。而且,本文方法比原有lmd方法的2倍频以及其它倍频的峰值更加显著。由此,验证了本文方法对往复压缩机强非平稳振动信号故障诊断的优越性。 图1 往复压缩机故障信号时域波形图 图2 往复压缩机故障信号频谱图 图3 传统l md方法的分解结果 图4 三次h e r mi t e插值l md法的分解结果 图5 传统l md方法P F 1分量的幅值频谱 图6 三次h e r mi t e插值l md方法P F 1分量的幅值频谱 针对往复压缩机振动信号的强烈非平稳特性,以及原有lmd方法中滑动平均法多次平滑的不足,结合三次hermite插值法的优良保形特性,提出了基于hermite插值的lmd方法。该方法以三次hermite插值对信号极值点进行包络,提高局部均值函数和包络估计函数的拟合精度。以往复压缩机传动机构为对象,通过与传统lmd方法的对比,验证了本文方法的优越性,实现了轴承间隙故障的准确诊断。 [1] 陈桂娟,王金东,刘耀芳,等.基于多重分形与奇异值分解的往复压缩机智能故障诊断技术 [J].压缩机技术,2013,(3):19-22. [2] Jonathan S Smith.The Local Mean Decomposition and Its Application to EEG Perception Data[J].Journal of the Royal Society Interface,2005,2(5):443-454. [3] 李志农,刘卫兵,易小兵.基于局域均值分解的机械故障欠定盲源分离方法研究[J].机械工程学报,2011,47(7):97-102. [4] CHENG Junsheng,ZHANG Kang,YANG Yu.An Order TraRcking Technique for the Gear Fault Diagnosis Using Local Mean Decomposition Method [J].Mechanism and Machine Theory,2012,55:67-76. [5] 张亢,程军圣,杨宇.基于有理样条函数的局部均值分解方法及其应用[J].振动工程学报,2011,24(1):97-103.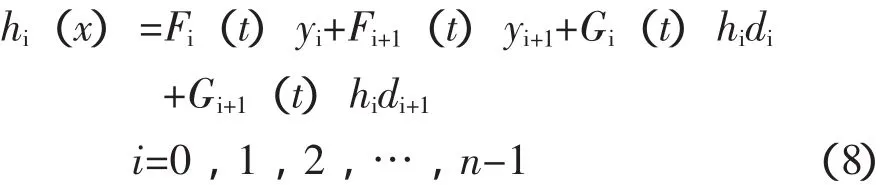

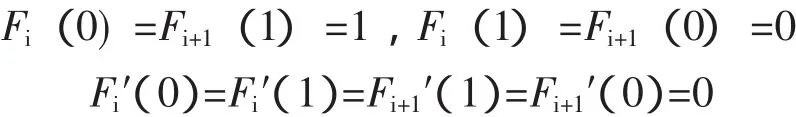

2.3 基于三次hermite插值的lmd算法

3 往复压缩机故障诊断技术



4 结论
