海洋钻采平台管子移运机械手运动学仿真

□ 王 勇 □ 刘树林 □ 杜 伟

上海大学 机电工程与自动化学院 上海 200072

在海洋石油钻井以及开采过程中，钻杆、油管及套管的搬运是最为繁重的工作任务之一，为此各种管子移运装置应运而生，最为典型的有大范围三维空间移运机械手。该机械手涉及到力学、机械学、电器液压技术、自动控制技术、传感器技术和计算机技术等科学领域［1］，能够实现管子的定点移运及随机移运，拥有自动控制及手动控制等多种方式。虽然该类型机械手已投入使用，但由于缺乏运动学理论研究，管子定点移运及自动控制模式未能得到很好地应用。

笔者分析了一种自动控制机械手，能够实现管子从堆放处至动力猫道或者从动力猫道至堆放处的智能搬运。讨论了机械手正运动学、逆运动学的求解方法，在MATLAB中建立其运动学仿真模型，验证了机械手结构设计的合理性，并利用蒙特卡洛法求出机械手的工作空间，为后续研究奠定了理论基础。

1 管子移运机械手结构分析

通常情况下，机械手的主要技术参数包括自由度、最大工作速度、承载能力、定位精度和重复定位精度等［2］。针对不同任务机械手的技术参数，结构设计应该各有侧重。

1.1 机械手总体结构

根据海洋钻井平台现场工作空间大，管子重量不一，直径粗细不均、长度也不相等的特征，移运机械手采取位置与姿态分开操作的结构。位置控制部分参照液压挖掘机等液压工程机械，采用液压缸驱动各机械臂来完成末端的定位。姿态部分（称之为叉臂）具有5个自由度，可灵活抓取方向放置不同的管子。管子移运机械手总体结构见图1，叉臂结构见图2。

1.2 机械手结构分析

参照图1、图2，机械手共有9个自由度，分析如下。

（1）整个机械手外部包括旋转平台，控制室绕固定基座转动，安装的位置传感器能实时精确地反馈旋转位置。

（2）内部臂绕旋转平台上下摆动；中间臂绕内部臂上下摆动；外部臂绕中间臂上下摆动；各摆动均通过液压缸实现，安装的位置传感器能实时精确地反馈各个液压缸伸出长度。

（3）外部臂与叉臂之间的转动，此自由度利用旋转脉冲编码器保持叉臂始终处于竖直状态。

（4）轭绕竖直方向的旋转运动，此运动通过液压马达实现，安装的位置传感器能实时精确地反馈旋转位置。

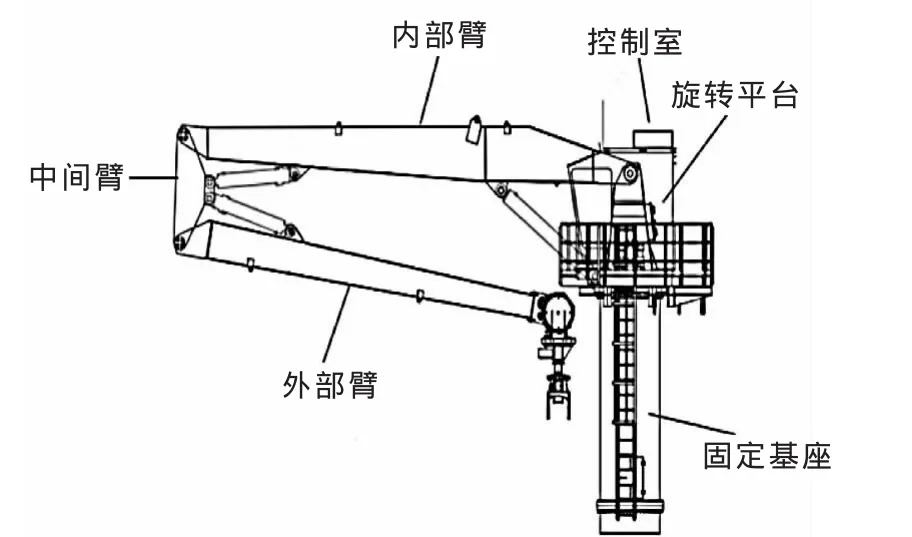
▲图1 管子移运机械手总体结构简图

▲图2 管子移运机械手叉臂结构简图

（5）轭沿竖直方向的上下运动，运动通过缓冲液压缸实现，可以缓冲机械臂对手爪的冲击力，安装的位置传感器、重力传感器能实时精确地反馈液压缸伸出长度、下面负载的重量。

（6）轭的两侧摆动，通过摆动液压缸实现，安装的位置传感器能实时精确地反馈液压缸伸出长度。

（7）抓手的张开闭合，此运动用于抓取管子，抓手有3种规格可以方便更换，轭的下面装有传感器，用于探测管子。

综上所述，管子移运机械手具有9个自由度，能够方便、快捷地完成管子在动力猫道与存放处之间的运输。9个自由度中，前4个自由度控制机械手终端的位置，后5个自由度控制机械手终端的姿态。液压动力单元集中安装于基座中，电控操作单元以及终端人机界面安装于控制室中，各传感器分布在执行零部件上。

2 管子移运机械手的运动学分析与仿真

机械手运动学研究是分析路径轨迹规划及运动控制的基础［3］，包括了正运动学分析和逆运动学分析。已知连杆参数和各个关节变量来求解指尖末端相对于给定坐标系的位置和姿态称之为正运动学，已知机械手连杆参数和指尖末端相对于固定坐标系的位置和姿态，来求解机械手各个关节变量的大小称之为运动学逆问题［4］。通过上节对机械手的结构分析，其末端抓手姿态主要靠传感器得到的实时反馈信息进行调整，不需要事先进行规划，所以对管子移运机械手的运动学分析及工作空间求解可以集中于前4个自由度，即从基座到外臂末端机械臂的运动学分析和外臂末端的工作空间求解。

2.1 机械手运动学方程建立及正运动学求解

建立机械手运动学方程常用的方法主要是标准的D-H方法和改进的D-H方法，两种方法基本原理相同，连杆分析思想一致，但坐标系表示方法不同，前者建立的连杆坐标系位于连杆末端，后者建立的连杆坐标系位于连杆前端［5］。本文中采用标准的D-H方法，建立管子移运机械手的连杆坐标系如图3。

根据所建立的连杆坐标系，按照标准D-H方法，确定各杆件结构参数和关节变量，见表1，表中：θ为关节角，是唯一变量；α为连杆转角；a为连杆长度；d为连杆偏距。

表1 机械手连杆参数和关节变量

▲图3 机械手连杆坐标系

基于表1中各参数，参照标准的D-H坐标转换公式，得出连杆坐标变换矩阵通式为：

式中：cθn+1=cosθn+1=cn+1；sθn+1=sinθn+1=sn+1。 另 c（θ2+θ3）=cos（θ2+θ3）=c23，s（θ2+θ3）=sin（θ2+θ3）=s23，以下各式简写类似。

各连杆的变换矩阵相乘，得出末端坐标系相对于基坐标系的齐次变换矩阵，即正运动学方程为：

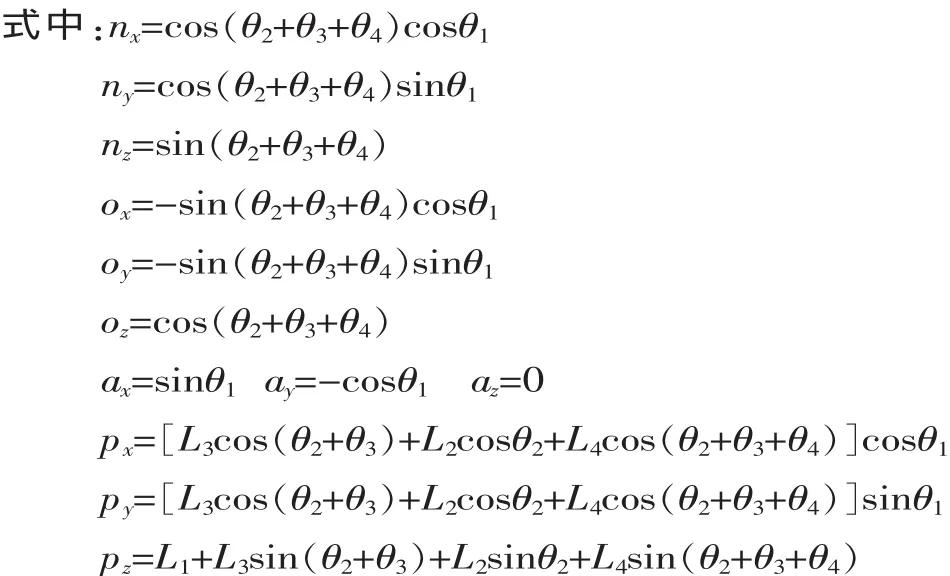
2.2 机械手逆运动学求解

机械手逆运动学求解方法主要分为数值方法和封闭解法［6］，对于简单的机械手一般用封闭解法，封闭解法又有反变换法、几何法等。本文采用反变换法求解如下。

将式（2）两边同时乘A1的逆，代入az=0可得：

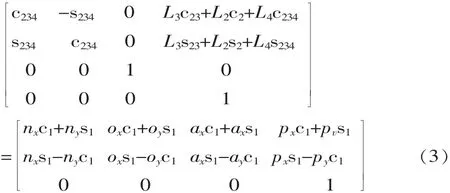
式（3）两边等式中第3行第4列元素相等，可得:

式（3）两边等式第2行第1列元素及第2行第2列元素分别相等，可得：

式（3）两边等式第1行第4列元素以及第2行第4列元素分别相等，可得：

整理、变换、化简上面两个方程，可得：

最后可得θ4:

2.3 机械手运动学MATLAB仿真验证

对正运动学仿真，给出结构设计参数：L1=8 m，L2=8 m，L3=2 m，L4=8 m，θ1＝0°，θ2＝0°，θ3＝-45°，θ4＝-45°。 在MATLAB程序中，为编程方便，用q表示关节角度。

（2）在MATLAB中建立机械手仿真图，如图4所示。

通过正运动学编程求解，得机械手末端X、Y、Z坐标 （仿真图 4 （b） 中 x、y、z 值） 分别为：9.4142，0，-1.414 2，与几何关系得出的结果相符，验证了正运动学的正确性。

逆运动学仿真，重新对关节角度赋值为：

在MATLAB/ROBOTICS工具箱下，编写逆运动学验证程序：

q= ［-pi/6 pi/6-pi/3-pi/3］;

drivebot（r,q）;

T=fkine（r,q）//%对关节值q求正解（末端位置）

q0=ikine（r,T）//%对末端位置求逆解（关节值）

MATLAB求解末端位置的逆解结果为：

▲图4机械手正运动学仿真图

▲图5 机械手逆运动学仿真图

q0=-0.523 6 0.523 6 -1.047 2 -1.047 2

可见，逆解结果q0与关节角度q所赋初值相等，验证了逆运动学的正确性。仿真图见图5。

3 管子移运机械手末端工作空间的求解

机械手工作空间指手臂末端所能达到的空间目标的集合，代表了机械手的活动范围，是衡量机械手工作能力一个重要的运动学指标［7］。通过对油管移运机械手的分析，关节角度θ1是作回转运动，所以本机械手工作空间可以只求解XOZ平面，之后关节角度θ1旋转相应角度范围即可得到整个工作空间。

本文采用蒙特卡洛法［8］求解管子移运机械手的工作空间。蒙特卡洛法是一种借助于随机抽样来解决数学问题的数值方法，广泛应用于描述某些随机的物理现象，其具体步骤如下。

（1）求解机械手运动学正解，得到机械手末端在参考坐标系中的位置向量。

（2）在MATLAB环境下，利用 Rand（）函数产生随机数形成各关节变量的随机值为：

▲图6 蒙特卡洛法末端工作空间图

式 中 ：θimin为 变量 θi转动范围的 最 小 值 ；θimax为变量 θi转动范围的最大值。

（3） 编写算法程序，使 式 （9） 循环N次 （此处N取80 000）， 得到每个关节变量的N个随机值。

（4） 将得到的随机值代入正运动学方程中，在MATLAB中调用绘图命令求解末端坐标点集，结果如图6所示。

4 结论

基于海洋平台管子移运的特殊性，针对具有9个自由度的移运机械手结构，分析了机构的正运动学解法、逆运动学解法，并在MATLAB中仿真验证了机构模型和解法的正确性；利用蒙特卡洛法求解了机械手末端在XOZ平面中的工作空间。一方面为进一步的轨迹规划和控制理论打下基础，更为重要的是对同性质机械手的设计和研究提供参照。

［1］ 熊有伦.机器人学［M］．北京：机械工业出版社，1993．

［2］ 马江.六自由度机械臂控制系统设计与运动学仿真［D］.北京：北京工业大学,2009.

［3］ 赵亮亮,马振书,穆喜辉，等.危险作业机器人机械臂设计及其运动学分析［J］.机械设计与制造,2011（8）:155-157.

［4］ 罗家佳,胡国清.基于 MATLAB的机器人运动仿真研究［J］.厦门大学学报（自然科学版）,2005,44（5）:640-644.

［5］ Corke P I.A Robotics Toolbox for MATLAB［J］.Robotics&Automation,IEEE,1996,3（1）:24-32.

［6］ 刘萍，陈莹.五自由度关节式机械手运动学分析及仿真［J］.制造业自动化,2011,33（19）:9-11.

［7］ Rastegar J,Fardanesh B.Manipulation Workspace Analysis Using the Monte Carlo Method［J］.Mechanism and Machine Theory,1990,25（2）:233-239.

［8］ 田海波,马宏伟.井下排爆机器人机械臂运动学及工作空间的分析［J］.矿山机械，2012,40（9）:105-108.