桩端约束力对钢管桩自由站立稳定性的影响

王景贵

(中海石油深海开发有限公司，广东深圳 518052)

近年来，随着海洋石油及天然气资源的开发，海洋结构物逐渐向深海发展，在海洋工程中应用广泛的钢管桩基础呈现出大直径、超长的特点。由于钢管桩桩径增大及承载力的提高，在打桩过程中选用的打桩锤能量增大，在设计时应对桩的自由站立稳定性进行校核，保障打桩系统的稳定性。针对钢管桩的自由站立稳定性问题，国内外学者开展了众多研究。陈波等［1］对某工程中桩基发生自由站立失稳的事故进行了分析，为工程技术人员提供了设计参考。刘润等［2-5］采用有限元方法模拟了桩的自由站立稳定性问题，对自由站立稳定性的影响因素进行了分析。董伟［6］研究了API规范与Timoshenko弹性稳定理论在分析钢管桩自由站立稳定性时的差异。赵亮［7］采用有限元方法与Timoshenko弹性稳定理论对比分析了钢管桩的自由站立稳定性。周龙等［8］考虑了波流荷载的动力联合作用，采用动力数值模拟方法分析了大直径钢管桩的自由站立稳定性。目前的研究中，对不同桩端约束条件的分析较少，本文采用数值模拟方法分析不同桩端约束及地基土体参数对钢管桩自由站立稳定性的影响，并与Timoshenko弹性稳定理论进行对比，提出了对工程设计有参考价值的建议。

1 数值分析方法

1.1 数值分析模型

采用有限元软件ABAQUS分析钢管桩的自由站立稳定性。建立直径D=2.8 m钢管桩模型，桩长L=70 m，壁厚δ=70 mm，自由站立段高度60 m，入土桩长10 m，密度ρ=7.85×103kg/m3，弹性模量E=210 GPa，泊松比μ=0.26，采用弹塑性本构模型。工程现场平均海水深度为70 m，最大波高为2.78 m，周期为7.0 s，海流顶层流速为0.65 m/s，底层流速为0.3 m/s。由于钢管桩自由站立高度为60 m，打桩作业为水下施工，仅考虑波浪和海流荷载，通过计算可得作用于桩顶的水平荷载为89.0 kN，弯矩荷载为－1 168.9 kN·m。桩端约束采用考虑固定端约束和考虑桩土相互作用两种情况。桩端为固定端约束时，钢管桩模型下端固定，上端自由，悬臂段高度为60 m。考虑桩土相互作用时，钢管桩悬臂段高度为60 m，入土10 m。土体模型尺寸采用高度为100 m，直径为100 m的圆柱形，本构模型采用Mohr-Coulomb弹塑性模型，容重 γ=17 kN/m3，侧限压缩模量 Es=20 MPa，粘聚力 c=30 kPa，内摩擦角φ=20°，泊松比μ=0.3。桩土之间的摩擦系数取0.5，数值分析模型如图1所示。

1.2 数值分析结果

在ABAQUS中采用Riks法分析不同桩端约束条件模型的自由站立稳定性，桩顶竖向荷载随桩顶水平位移的变化曲线如图2所示。由图2可知，采用固定端约束时桩顶竖向荷载为73.9 MN时桩顶水平位移发散，说明屈曲荷载为73.9 MN，而考虑桩土相互作用时屈曲荷载为33.3 MN。由于固定端对钢管桩约束作用较强，在实际工程中假设桩底为固定端约束分析钢管桩的自由站立稳定性时，计算的屈曲荷载偏大，因此在数值分析中应充分考虑桩土相互作用的影响。

图1 数值分析模型

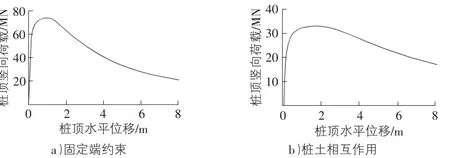
图2 桩顶竖向荷载随桩顶水平位移的变化曲线

1.3 数值分析方法与Timoshenko法对比

董伟［6］，赵亮［7］应用Timoshenko弹性稳定理论分析了钢管桩的自由站立稳定性。对于杆件底端固定，顶端为自由端，考虑杆件自重作用以及桩顶端受到外荷载作用时的屈曲荷载Pcr可按下式计算:其中，E为钢管桩的弹性模量;I为钢管桩截面对形心轴的最小惯性矩;l为自由站立段高度;q为桩身自重均布荷载。采用Timoshenko法计算数值分析中钢管桩模型的屈曲荷载，并与数值分析中的计算值进行对比，结果如表1所示。

表1 屈曲荷载计算值对比

由表1可知，Timoshenko法与采用固定端约束的数值分析结果较为相符，两种方法在计算中均假设桩端为固定端约束。而Timoshenko法计算的桩身屈曲荷载约为考虑桩土相互作用的数值分析结果的2.4倍，计算的结果偏于危险。

2 土体强度参数对自由站立稳定性的影响

2.1 粘聚力的影响

为研究粘聚力c对钢管桩自由站立稳定性的影响，在数值分析中 c分别取 20 kPa，25 kPa，30 kPa，35 kPa 和 40 kPa，采用 Riks法计算临界屈曲荷载，计算结果如图3所示。由图3可知，钢管桩的桩身屈曲荷载随地基土体粘聚力的改变而变化，当粘聚力增大时，桩身的屈曲荷载增大，桩身的自由站立稳定性提高。

2.2 内摩擦角的影响

为研究内摩擦角φ对钢管桩自由站立稳定性的影响，在数值分析中 φ 分别取10°，15°，20°，25°和30°，采用 Riks法计算临界屈曲荷载，计算结果如图4所示。由图4可知，钢管桩的桩身屈曲荷载随地基土体内摩擦角的改变而变化，当内摩擦角增大时，桩身的屈曲荷载增大，桩身的自由站立稳定性提高。

图3 粘聚力对屈曲荷载的影响

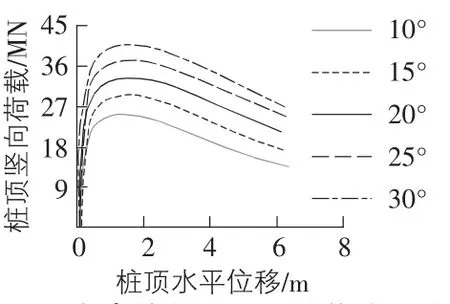
图4 内摩擦角对屈曲荷载的影响

3 结语

基于数值方法分析了不同桩端约束条件及地基土体参数对钢管桩自由站立稳定性的影响，并与Timoshenko弹性稳定理论进行了对比，具体结论如下:

1)进行自由站立稳定性分析时，假设桩端为固定端约束与实际约束情况不符。由于固定端对钢管桩约束作用较强，假设桩底为固定端约束时计算的屈曲荷载偏大。2)Timoshenko法计算的屈曲荷载与采用固定端约束时数值分析的结果较为相符，而与考虑桩土相互作用的数值分析结果相比为其2.4倍。3)钢管桩的自由站立稳定性与地基土体的性质有关，桩身屈曲荷载随粘聚力及内摩擦角的改变而变化，当土体粘聚力或内摩擦角增大时，桩身的屈曲荷载均随之增大，桩身的自由站立稳定性提高。

［1］陈 波，闫澍旺，樊之夏.桩基平台桩的可打入性和自由站立强度分析［J］.中国海上油气(工程)，2001，13(6):1-5.

［2］刘 润，禚瑞花，闫澍旺，等.超长桩施工中桩身稳定性的三维非线性有限元分析［J］.天津大学学报，2006，39(3):257-263.

［3］刘 润，闫澍旺，毛永华，等.海洋工程中桩身自由站立稳定性影响因素分析［J］.海洋工程，2006，24(3):6-13.

［4］高喜峰，刘 润，谭振东，等.基于桩土相互作用的桩体自沉及屈曲稳定性研究［J］.中国造船，2012，53(2):113-121.

［5］Liu Run，Yan Shu-wang，Li Zhi-hua.Soil Plug Effect Prediction and Pile Driveability Analysis for Large-diameter Steel Piles in Ocean Engineering［J］.China Ocean Engineering，2009，23(1):107-118.

［6］董 伟.海洋采用平台大直径超长桩动力沉桩分析方法研究［D］.天津:天津大学博士论文，2009.

［7］赵 亮.海洋石油平台大直径超长桩贯入特性及原位测试研究［D］.天津:天津大学博士论文，2012.

［8］周 龙，刘 润，张金凤，等.考虑波流联合作用的大直径钢管桩自由站立稳定性分析［J］.岩土工程学报，2014(3):2-3.