分数槽集中绕组嵌入式永磁同步电机设计

王玉彬 孙建鑫

（中国石油大学（华东）机电工程学院 青岛 266580）

1 引言

随着稀土永磁材料钕铁硼（NdFeB）性价比的不断提高，永磁电机（PM）以其高效率、高功率密度、动态响应特性好等显著优点在工业驱动和伺服控制系统等领域得到了快速发展[1,2]。通常，径向磁场永磁同步电机可以分为表面贴装式永磁同步电机（SPM）和嵌入式永磁同步电机（IPM）两大类。其中，SPM 电机为隐极式电机，直轴电感与交轴电感近似相等，凸极比为1，因此，其磁阻转矩为零，输出转矩中仅包含永磁转矩。此外，由于永磁体置于转子铁心表面，且永磁体的磁导率接近气隙的磁导率，致使气隙磁场调节困难，恒功率运行范围较窄[3,4]。与之比较而言，IPM 电机为凸极式电机，它秉承了SPM 电机所具有的高效率、高功率密度等优点，同时输出转矩又包含了凸极效应所产生的磁阻转矩，而且气隙磁场易调节，具有较为宽广的恒功率运行范围，在混合动力汽车驱动领域得到了广泛的应用[5-8]。

IPM 电机的绕组配置通常采用分布绕组和集中绕组两种形式。其中，分数槽集中绕组嵌入式永磁同步电机（FCW—IPM）具有端部短、铜耗低、效率高、槽利用率高、定位力矩小、可实现自动绕线等显著优点，已成为近年来国内外专家学者关注的热点之一[9-14]。对于混合动力汽车用驱动电机而言，由于汽车空间的限制，多采用扁平结构，因此，FCW—IPM 电机短端部的特点使其更加适合混合动力汽车运行工况。鉴于此，本文基于“V”形永磁体结构能够有效聚磁的特点，设计并分析了一类混合动力汽车驱动用极槽数相近的FCW—IPM 电机。该类电机不仅具有IPM 电机的固有优点，而且由于其端部较短，能够有效地降低驱动电机所占的物理空间。

本文首先分析了FCW—IPM 电机的极槽数配合选择依据，然后基于所得分析结果，对一台12 槽/10极FCW—IPM 电机的磁场分布、气隙磁通密度、相绕组反电动势、稳态输出转矩以及定位力矩等静态电磁特性进行了有限元分析。为分析FCW—IPM 电机的电感特性，提出了一种交直轴电流全解耦与“冻结磁导率法”相结合的方法，详细分析了交叉饱和以及转子位置对交直轴电感的影响。最后，设计并制造了一台额定功率为10kW 的样机，样机实验验证了理论分析的正确性。

2 极槽数配合的选择

对于 FCW—IPM 电机而言，其每极每相槽数（SPP）为分数。设电机定子槽数为Q，极对数为p，则对于极槽数相近的IPM 电机有

通常，只有满足下式的极槽数配合才能够实现分数槽配置[15]，即

式中 m——电枢绕组的相数；

t——Q 和p 的最大公约数（GCD）。

体现在槽电动势星形图上时，即为每槽电动势向量的重复次数，也即单元机数目。

由于绕组系数kw正比于IPM 电机输出转矩中的永磁转矩分量，因此在确定极槽数配合时，应尽量获得较大的绕组系数。为此，表1 给出了几种常见极槽数相近的IPM 电机极槽配合，且均为绕组系数大于0.9 的极槽数组合。

表1 绕组系数Tab.1Windings factors

表1 给出的几种常见极槽数配合中[16]，9 槽/8极组合受单边磁拉力影响较大[17]，18 槽/16 极和24槽/22 极组合虽然具有较高的绕组系数，但对混合动力汽车驱动电机的运行工况而言，由于电机转速较高，使得供电逆变器频率增高，电力电子功率器件的开关损耗也会随之增加。因此，综合考虑，选取12 槽/10 极组合较为适宜。图1 所示为12 槽/10极FCW—IPM 电机结构及其绕组分布。可以发现，采用集中绕组后，无论单层绕组还是双层绕组，各相绕组的磁动势分布在空间都是分离的，从而使得该类电机同时具备较强的容错运行能力，能有效提高驱动系统的可靠性[18]。

图1 FCW—IPM 电机结构Fig.1 Configuration of FCW—IPM machine

3 电磁特性分析

3.1 气隙磁场分布

基于二维有限元法对一台12 槽/10 极的FCW—IPM 样机进行分析，得到电机的空载磁场分布如图2 所示。为分析FCW—IPM 电机的弱磁特性，在电枢绕组中施加纯去磁电流Id（即Iq=0），可以得到不同去磁电流Id时电机的气隙磁通密度分布如图3 所示，可以发现，随着去磁电流Id的增大，气隙磁通密度显著减小，因此能够有效降低电机高速运行时的反电动势，说明该类电机具有较好的弱磁性能。

图2 空载磁场分布Fig.2 Magnetic field distribution at no load

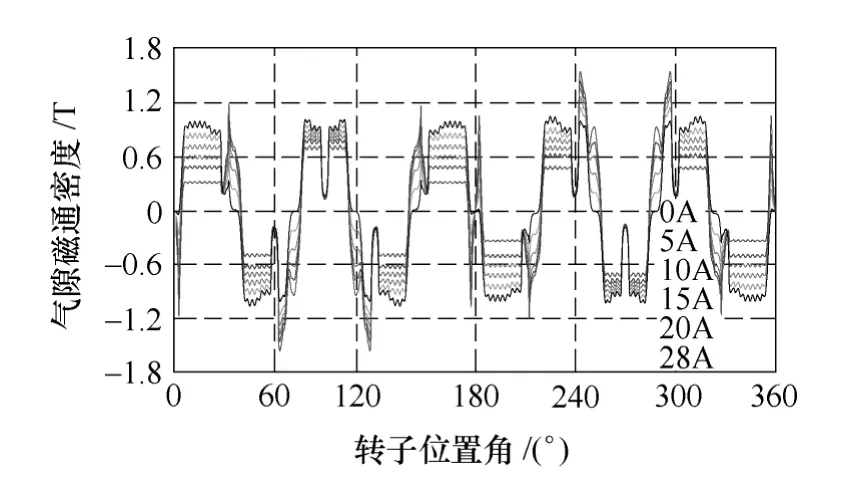
图3 不同弱磁电流时的气隙磁通密度分布Fig.3 Distribution of magnetic flux density of the airgap under various flux-weakening currents

3.2 反电动势

计算FCW—IPM 电机的空载反电动势时，根据有限元计算得到的结果，首先计算出每个定子齿中的磁通量，然后根据相绕组的分布情况，计算出每相绕组匝链的永磁磁链，由式计算可得反电动势

式中 e——反电动势的瞬时值；

ψPm——相绕组匝链的永磁磁链；

θr——转子位置角的机械角度；

n——电机转速。

取单层绕组与双层绕组的槽满率及绕组线径均相同，于是可以得到单层与双层绕组的空载反电动势分布如图4 所示。由图4 可见，双层绕组配置的空载反电动势波形具有较高的正弦度，单层绕组的空载反电动势则近似为梯形波。

图4 空载反电动势Fig.4 Back EMF at no load

为考察两种绕组配置的谐波分布及含量，分别对其进行傅里叶分解，得到单层绕组与双层绕组的谐波含量及其分布情况如图 5 所示。额定转速下（nN=1 000r/min），双层绕组配置的反电动势基波有效值为135.79V，谐波含量为4.74%；单层绕组反电动势的基波有效值略高于双层绕组，为138.12V，这是因为单层绕组的绕组系数为0.966，高于双层绕组的绕组系数0.933，但是其谐波含量高达6.75%。无论单层还是双层绕组，其高次谐波主要包含齿槽效应以及永磁体极间导磁桥局部饱和引起的3 次、5次、7 次和11 次谐波。

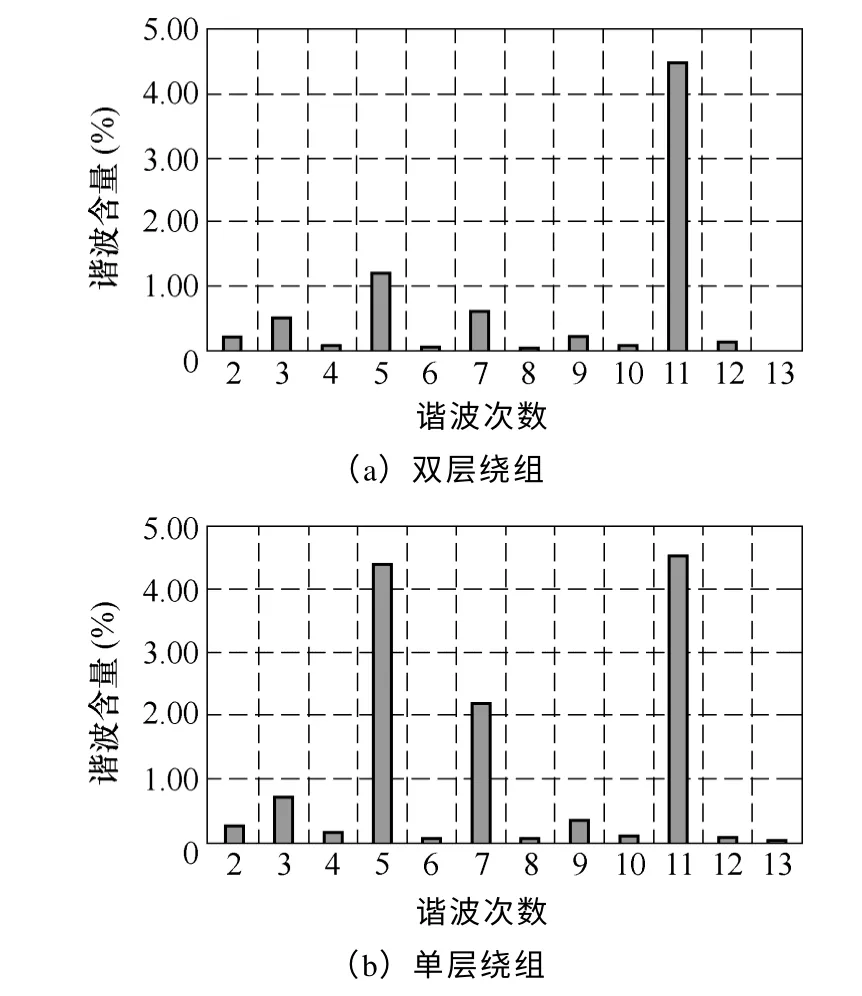
图5 空载反电动势谐波含量Fig.5 Harmonic content of the back EMF at no load

3.3 稳态转矩

稳态转矩是衡量FCW—IPM 电机性能的一个重要指标，图6 所示为采用有限元法计算得到的FCW—IPM 样机的稳态转矩波形。若定义电机的转矩脉动为转矩最大值与最小值之差除以平均转矩，则由图 6 可以得到，FCW—IPM 电机的转矩脉动为16.5%，这主要是因为采用集中绕组后，相绕组的磁动势为矩形波，与分布式绕组的梯形波磁动势相比，谐波含量较大，致使FCW—IPM 电机的转矩脉动相对较大，若采用谐波电流注入法等控制策略，可以获得较好的动态性能。

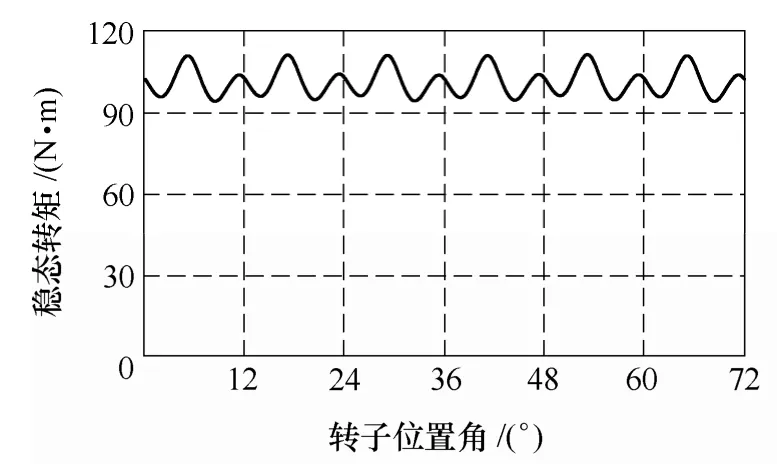
图6 稳态转矩Fig.6 Distribution of the steady torque

3.4 定位力矩

由于FCW—IPM 电机采用分数槽结构，因此，无需采用转子斜槽等附加措施，即可有效地抑制其定位力矩。图7 给出了采用麦克斯韦张量法及虚功法计算得到的定位力矩波形，可以发现，其定位力矩的峰峰值为2.15N·m 左右，仅为额定转矩的2.3%。

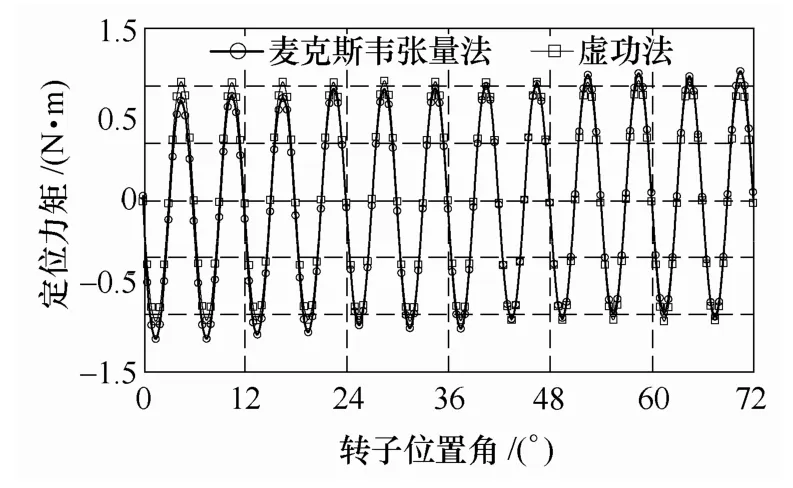
图7 定位力矩Fig.7 Distribution of the cogging torque

3.5 电感特性

准确计算IPM 电机的直轴电感Ld和交轴电感Lq是获得良好的稳态及动态控制性能的基础。通常，采用有限元法计算永磁电机的电感时，首先计算某一相绕组所匝链的永磁磁链和电枢电流所产生的磁链之和，然后再减去电枢电流为零时相绕组匝链的永磁磁链，将所得相绕组磁链数据代入式（4）进行帕克变换[19]，得到电机的直轴及交轴磁链，分别除以相应的直轴电流Id和交轴电流Iq，即可得电机的直轴及交轴电感。

式中 ψd，ψq——直轴磁链和交轴磁链；

ψa，ψb，ψc——相绕组磁链；

θ ——A 相绕组轴线与直轴的电角度。

上述方法的前提是假定电枢反应前后的永磁磁链不变，也即忽略了定转子铁心磁导率变化对永磁磁链的影响，而且也没有考虑D 轴和Q 轴之间交叉耦合的影响，导致电感参数计算不准确，为此，文献[19,20]提出一种改进的“冻结磁导率法”来计算绕组的电感。采用“冻结磁导率法”计算绕组电感时，首先计算永磁体和电枢电流共同作用时的总磁链，存储记忆此时各个单元的磁导率，然后将永磁体区域设为气隙，计算电枢电流单独作用时绕组所匝链的磁链，经式（4）进行帕克变换，得到电机的直轴及交轴磁链，进而计算获得直轴和交轴电感。“冻结磁导率法”既考虑了电枢反应前后永磁磁链的变化，又计及了交直轴电流交叉耦合的影响，能够准确的描述某一转子位置下交、直轴电感随电枢电流的变化情况。

图8 定转子相对位置Fig.8 Relative position between the stator and rotor

图9 计及交叉饱和的Ld和LqFig.9 Distribution of both Ldand Lqconsidering the cross saturation

图8 所示为有限元计算时转子的初始位置，为方便施加直轴电流Id，将转子顺时针旋转15°，使得A 相绕组轴线与D 轴的电角度θ 为零。在该位置采用“冻结磁导率法”计算电机的交直轴电感，得到其变化规律如图9 所示。当直轴电流Id和交轴电流Iq都很小时，直轴磁路的饱和程度主要取决于永磁磁动势，且直轴磁路饱和程度较低，交轴电流Iq对直轴磁链的影响很小，因此电感Ld较大，如图9a中的区域A 所示。随着交轴电流Iq的增大，对直轴磁链的影响增强，Ld的变化规律是先减小后增大，如图9a 中的区域B 所示。图9b 中，当Id和Iq都比较小时，交轴磁路不饱和，且直轴电流Id对交轴电感Lq的影响很小，此时的交轴电感Lq较大，如区域C 所示。随着Iq的增大，交轴磁路趋于饱和，Lq逐渐减小。当Iq和Id较大时，此时交轴磁路受到交轴磁场和直轴磁场的共同作用，饱和程度加强，因此Lq较小，如图9b 中的区域D 所示。

由图9 可见，“冻结磁导率法”准确反映了某一转子位置下的交直轴电感变化及其相互耦合影响，但是该方法没有计及定转子相对位置对绕组电感的影响。若采用该方法分别计算不同定转子相对位置下的交直轴电感，则计算量庞大，不易实现。为此，本文提出一种交直轴全解耦与冻结磁导率相结合的方法，较为全面的描述了交叉耦合和定转子相对位置变化对电机交直轴电感的影响规律。

当一台IPM 电机的设计参数确定后，影响其电感参数的主要因素是定转子的相对位置和直轴、交轴磁路中各个计算单元的相对磁导率μr的变化。因此，分析直轴电感Ld随转子位置的变化规律时，主要研究对象是直轴磁路中各个计算单元的相对磁导率μr。而且，无论是直轴电流Id对直轴磁路中各个计算单元的影响，还是交轴电流Iq对直轴磁路交叉耦合的影响，都可归结为直轴磁路中各个计算单元磁导率μr的变化。因此，可以假定交轴电流Iq为0，从而消除交轴电流的交叉耦合影响，采用改变直轴电流Id的大小来模拟直轴电流和交轴电流共同作用对直轴磁路计算单元磁导率μr的影响，从而使得交直轴电流的完全解耦[19,20]。同理，分析交轴电感Lq随转子位置的变化规律时，可假定直轴电流为0，以研究交轴电感Lq随转子位置的变化规律。因此，将“冻结磁导率法”与交直轴全解耦计算方法相结合，不仅可以研究某一转子位置下的交直轴电感变化及其相互耦合影响，而且也能够分析定转子相对位置变化对交直轴电感的影响。

根据图4 所示的空载反电动势波形可知，其A相绕组的相位角为75°电角度。对于三相绕组而言，当某相电流达到最大值时，定子电流形成的基波旋转磁场方向与该相绕组轴线重合。因此，当A 相去磁电流施加最大值时，将转子顺时针旋转15°（电角度75°）后，可使定子基波旋转磁场方向与A 相绕组轴线重合，此时的基波电枢磁场方向与永磁磁场方向完全相反，起到纯去磁作用，也即Iq为0，可得到直轴电感Ld随转子位置的变化规律如图10a 所示。可以发现，当退磁电流Id较小时，直轴电感受定转子相对位置的影响较大，随着直轴去磁电流的增大，直轴磁路饱和程度增强，直轴电感Ld的波动幅度减小，同时其幅值也逐渐降低。图10b 给出了交轴电感Lq随转子位置的变化规律。当Iq较小时，直轴磁路不饱和，Lq较大，其波动幅度也较大。随着Iq的增大，交轴磁路的饱和程度增强，Lq随之减小，波动幅值也逐渐降低。

图10 Ld和Lq随转子位置的变化规律Fig.10 Variation of both the Ldand the Lqwith change of rotor position

4 样机实验

为验证上述分析的正确性，设计并制造了一台额定功率为10kW 的样机（主要尺寸参数见表2），图11 为样机的定转子冲片及组装样机照片。样机在额定转速 1 000r/min 运行时的实测空载反电动势波形如图12 所示，对比图4 与图12 可以发现，仿真波形与实测波形吻合。样机实测反电动势幅值为180.1V，与反电动势仿真波形幅值192.02V 相比较，实测值降低了6.25%。由于有限元计算时设定的叠片系数与样机制造时的实际叠片系数不一致以及忽略端部漏磁的影响，故实测波形幅值略低于仿真波形。

表2 FCW—IPM 样机尺寸参数Tab.2 Technical data of FCW—IPM prototype

图11 样机图片Fig.11 FCW—IPM prototype

图12 实测空载反电动势波形Fig.12 Measured back EMF waveform at no load

5 结论

本文设计了一种极槽数相近的 FCW—IPM 电机，给出了其槽极数选择依据，分析了其磁场分布、气隙磁通密度、相绕组反电动势、稳态输出转矩以及定位力矩等静态电磁特性，采用交直轴电流全解耦与“冻结磁导率法”相结合的方法，重点分析了交叉饱和以及转子位置对交直轴电感的影响，获得了交叉饱和以及转子相对位置对交直轴电感的影响变化规律，为实现高性能控制奠定了基础。最后，设计并制造了一台额定功率为10kW 的样机，样机实验验证了理论分析的正确性。

[1]Zhu Z Q,Howe D.Electrical machines and drives for electric,hybrid,and fuel cell vehicles[J].IEEE Proceedings,2007,95(4):746-765.

[2]Chau K T,Chan C C,Liu C.Overview of permanentmagnet brushless drives for electric and hybrid electric vehicles[J].IEEE Transactions on Industrial Electronics,2008,55(6):2246-2257.

[3]唐任远.现代永磁电机理论与设计[M].北京：机械工业出版社,1997.

[4]Chong L,Rahman M F.Saliency ratio derivation and optimisation for an interior permanent magnet machine with concentrated windings using finiteelement analysis[J].IET Electric Power Applications,2010,4(4):249-258.

[5]Dutta R,Rahman M F.Design and analysis of an interior permanent magnet(IPM) machine with very wide constant power operation range[J].IEEE Transactions on Energy Conversion,2008,23(1):25-33.

[6]Stumberger B,Stumberger G,Hadziselimovic M,et al.Design and finite-element analysis of interior permanent magnet synchronous motor with flux barriers[J].IEEE Transactions on Magnetics,2008,44(11):4389-4392.

[7]Barcaro M,Bianchi N,Magnussen F.Design considerations to maximize performance of an IPM motor for a wide flux–weakening region[C].International Conference on Electrical Machines,2010:1-7.

[8]Barcaro M,Alberti L,Faggion A,et al.IPM machine drive design and tests for an integrated starteralternator application integrated starter-alternator application[C].IEEE International Conference on Industry Applications Society Annual Meeting,2008:1-8.

[9]杨浩东,陈阳生.分数槽永磁同步电机电磁振动的分析与抑制[J].中国电机工程学报,2011,31(24):83-89.Yang Haodong,Chen Yangsheng.Electromagnetic vibration analysis and suppression of permanent magnet synchronous motor with fractional slot combination[J].Proceedings of the CSEE,2011,31(24):83-89.

[10]陈益广,潘玉玲,贺鑫.永磁同步电机分数槽集中绕组磁动势[J].电工技术学报,2010,25(10):30-36.Chen Yiguang,Pan Yuling,He Xin.Magnetomotive force in permanent magnet synchronous machine with concentrated fractional-slot winding[J].Transactions of China Electrotechnical Society,2010,25(10):30-36.

[11]Ayman M,Refaie E L.Fractional-slot concentratedwindings synchronous permanent magnet machines:opportunities and challenges[J].IEEE Transactions on Industrial Electronics,2010,57(1):107-120.

[12]Tangudu J K,Jahns T M,Refaie El A.Unsaturated and saturated saliency trends in fractional-slot concentrated-winding interior permanent magnet machines[C].IEEE International Conference on Energy Conversion Congress and Exposition,2010:1082-1089.

[13]Chong L,Dutta R,Rahman M F.Design of an interior permanent magnet machine with concentrated winding for field weakening applications[C].IEEE International Conference on Electric Machines &Drives,2009:1985-1992.

[14]Lindh P M,Jussila H K,Niemela M,et al.Comparison of concentrated winding permanent magnet motors with embedded and surface-mounted rotor magnets[J].IEEE Transactions on Magnetics,2009,45(5):2085-2089.

[15]叶金虎.无刷直流电动机的分数槽电枢绕组和霍尔元件的空间配置[J].微特电机,2001,4:8-11,14.Ye Jinhu.Fractional-slot armature windings and hall elements placement for brushless DC motor[J].Small&Special Machines,2001,4:8-11,14.

[16]Fornasiero E,Alberti L,Bianchi N,et al.Considerations on selecting fractional–slot windings[C].IEEE International Conference on Energy Conversion Congress and Exposition,2010:1376-1383.

[17]高宏伟,松本健二,陈宝.无刷直流电动机的径向不平衡电磁力对振动噪声的影响及其削弱方法[J].微特电机,2007,4:1-3,7.Gao Hongwei,Song Benjianer,Chen Bao.Influence and reduction of radial electromagnetic force on vibration and noise in brushless DC motors[J].Small&Special Machines,2007,4:1-3,7.

[18]Bianchi N,Pré M D,Grezzani G,et al.Design considerations on fractional-slot fault-tolerant synchronous motors[C].IEEE International Conference on Electric Machines &Drives,2005:902-909.

[19]李和明,张健,罗应立,等.考虑交叉饱和影响的永磁同步电机稳态参数有限元分析[J].中国电机工程学报,2012,32(12):104-110.Li Heming,Zhang Jian,Luo Yingli,et al.Finite element analysis of PMSM steady state parameters considering cross-saturation effect[J].Proceedings of the CSEE,2012,32(12):104-110.

[20]李景灿,廖勇.饱和对埋入式永磁同步电机电感特性的影响[J].重庆大学学报,2009,32(11):1285-1290.Li Jingcan,Liao Yong.Impact of saturation on the characteristic of inductance of permanent magnet synchronous motors[J].Journal of Chongqing University,2009,32(11):1285-1290.