直流偏磁下不同磁化曲线对变压器铁心损耗仿真的影响

张艳丽 彭志华 谢德馨 白保东

（沈阳工业大学电气工程学院 沈阳 110870）

1 引言

直流偏磁条件下变压器铁心损耗计算是目前备受关注的热点和难点问题之一[1-4]。对于同一变压器算例，若采用铁心材料磁化特性的不同表述，其相应的损耗计算结果将产生明显差别。因此，正确选择变压器铁心材料磁化特性的描述方法对其磁场、损耗等仿真结果有重要影响。特别是在能源需求不断增长、变压器单台容量不断提升的今天，考察不同磁化特性描述方法之间的区别更具有特殊意义。磁化曲线是表征物质磁通密度与磁场强度依赖关系的曲线。按测量方法与测量外部环境的不同，磁性材料的磁化曲线可分为平均磁化曲线、交流磁化曲线、直流磁化曲线、交流偏磁磁化曲线和交直流共同作用下的磁化曲线等类型。目前在变压器直流偏磁问题的仿真计算中，关于铁心材料选取何种磁化曲线的研究尚未引起足够重视。尽管已开展了一些专题研究[5-7]，但由于问题的复杂性和测试条件的限制，有些文献在进行直流偏磁情况下的仿真计算时，直接采用标准条件下测得的交流磁化曲线。这种简化处理将对计算结果的精度产生影响。

本文利用从德国进口的一套具有直流偏磁测试功能的爱泼斯坦方圈系统，测量了有、无偏磁条件下硅钢片材料的磁化特性，阐述了不同磁化曲线的定义方式及提取方法。针对变压器制造企业提供的实际变压器模型，在直流偏磁下对铁心材料赋予不同的磁化曲线，分别进行了有限元仿真计算。自行设计了实验测试电路，在直流偏磁条件下对实际变压器模型进行了空载损耗测量。最后，将仿真结果与实验结果进行了对比，分析了不同磁化曲线对铁心损耗计算结果的影响，为提高直流偏磁下电力变压器电磁仿真与损耗计算精度提供参考依据。

2 硅钢片磁化曲线的不同表述及提取

众所周知，铁磁材料在交变磁化过程中磁场强度H 与磁通密度B 变化一周期所构成的曲线称为磁滞回环。磁场计算中所用的磁化曲线是基于磁滞回环按不同方式得出的。本文以30ZH120 取向电工钢片的爱泼斯坦（Epstein）方圈试验数据为依据，详细阐述不同磁化曲线的定义方式及适用情况。

2.1 无偏磁电流的磁化曲线

无偏磁电流的磁化曲线指在Epstein 方圈试验中励磁电流只含有交流成分时测得的特性曲线。

（1）交流磁化曲线。交流磁化曲线定义为不同磁化强度下由磁场强度波形的峰值Hm与磁通密度峰值Bm构成的一组数据生成的曲线，即Bm-Hm曲线[8]。交流磁化曲线有时不能直接在交流磁滞回环上直接找到对应的Bm-Hm点。例如：磁特性饱和前，如图1 所示，在磁滞回环上当B 达到最大值Bm时，H 并未达到最大值Hm，即Bm和Hm未出现在交流磁滞回环的同一点。交流磁化曲线广泛用于交流电压激励下的磁性材料磁场仿真计算中。

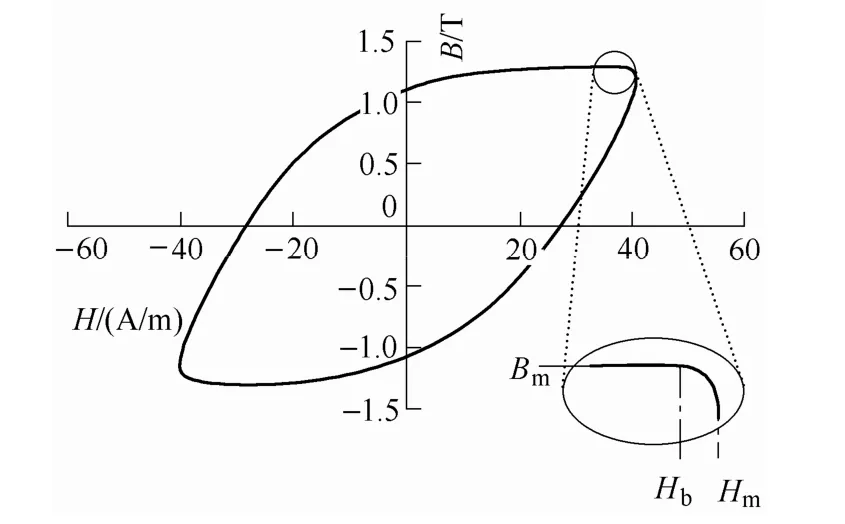
图1 Bm、Hm和Hb的说明Fig.1 Illustration of Bm,Hmand Hb

（2）直流磁化曲线。在直流激励下，缓慢改变励磁电流的大小，将得到直流磁滞回环。直流磁滞回环不包含涡流效应。但完全直流条件下测量B-H曲线有困难，因此直流磁化曲线通常是在较低频率下将交流磁滞回环族上一系列Bm-Hb点连线近似为直流磁化曲线[4]。其中，Hb为磁通密度达到最大值Bm时对应的磁场强度，如图1 所示。这样近似的合理性在于：一是测量频率较低，涡流效应不明显；二是磁滞回环Bm附近B 值变化不大，该点B 随时间的变化率可近似为零，感应涡流也为零，所以Bm-Hb连线就只表征不含有涡流效应的直流磁化特性。

图2 对比了由不同频率的交流磁滞回环近似得到的直流磁化曲线。由该图可知，在3Hz 频率下测得的直流磁化曲线与25Hz 和50Hz 的并不是完全重合，可见频率对直流磁化曲线的提取是有影响的。本文建议当近似直流磁化曲线时，在测量设备允许的条件下应该尽可能地使用低频的交流磁滞回环。

图2 由不同频率的交流磁滞回环近似的直流磁化曲线Fig.2 DC magnetization curves obtained from different AC magnetic hysteresis loops under different frequencies

直流磁化曲线主要用于涡流场数值计算中。因为涡流场求解方程已包括涡流项，在描述硅钢片材料磁性能时应采用不含涡流效应的直流磁化曲线。

（3）平均磁化曲线。交流磁滞回环顶点的连线称为平均磁化曲线（或基本磁化曲线）。在生成某一磁滞回环的顶点数据时，本文将极径最长的点作为顶点，也就是磁滞回环上（i=1,2,…,N）值最大的点，其中N 为一个时间周期波形的采样次数。

图3 给出了50Hz 时的交流磁滞回环族及相应的交流磁化曲线和平均磁化曲线。

图3 交流磁滞回环及交流磁化曲线和平均磁化曲线（50Hz）Fig.3 AC magnetic hysteresis loops,AC and average magnetization curves (50Hz)

2.2 含偏磁电流的磁化曲线

利用Epstein 方圈进行直流偏磁特性测量时，直流成分是通过在交流励磁电流信号中叠加一个直流偏置电流实现的[9-12]。测量结果中磁场强度波形是通过将交直流合成的电流波形除以等效的平均磁路长度得到的，是直流和交流共同作用下的磁场强度（以下称为交直流磁场强度）。而磁通密度波形则根据电磁感应定律计算得到，但由于直流电流产生的磁通密度（称为直流偏置磁通密度ΔB）对时间的微分为零，所以测得的磁通密度波形为未考虑直流偏置磁通密度的仅含有交流成分的磁通密度。

（1）交流偏磁磁化曲线。交流偏磁磁化曲线为偏磁电流一定时由交直流磁场强度波形的峰值与不含直流偏置磁密的磁通密度峰值生成的一组数据连接的曲线[4]。图4 给出了偏置磁场Hdc=178A/m 时交流偏磁磁滞回环族和交流偏磁磁化曲线。由于该磁化曲线未能考虑偏置磁通密度的影响，所以不能直接应用到直流偏磁设备的数值计算中。

图4 交流偏磁磁滞回环族和交流偏磁磁化曲线Fig.4 AC bias magnetic hysteresis loops and AC bias magnetization curve

（2）交直流共同作用下的磁化曲线。考虑了直流偏置磁通密度的磁化曲线就叫交直流共同作用下的磁化曲线[4,13]。文献[7]给出了生成该磁化曲线的具体方法：首先，以低频下的直流磁化曲线为基准曲线；然后，将图4 中交流偏磁磁滞回环中某个回环所有点整体向上平移一个直流偏置磁通密度ΔB，使得该回环正顶点落在基准直流磁化曲线上。同理，将所有交流偏磁磁滞回环做同样处理就可以形成新的磁滞回环族，如图5 所示；最后，提取该磁滞回环族中顶点值并连线就得到交直流共同作用下的磁化曲线。交直流共同作用下的磁化曲线可以用于直流偏磁变压器的仿真计算中。

图5 交直流共同作用下的磁滞回环族Fig.5 Magnetic hysteresis loops with AC and DC applied

利用上述方法，本文测量并生成了偏置磁场依次为178A/m、350A/m 和490A/m 的交直流共同作用下的磁化曲线，如图6 所示。由此图可以看出，这3 条磁化曲线完全重合，而且，它们也与第2.1节描述的直流磁化曲线重合。究其原因，生成直流偏磁磁化曲线的过程是以直流磁化曲线为基准曲线来平移交流偏磁磁滞回环，使其磁场强度最大值等于直流磁化曲线上对应的磁场强度，最终该回环顶点落在了直流磁化曲线上。因此，从原理上分析该方法得到的交直流共同作用下的磁化曲线在数值上和直流磁化曲线是同一条曲线。

图6 交直流共同作用下的磁化曲线与直流磁化曲线Fig.6 Magnetization curves with DC and AC applied and DC bias magnetization curve

因此，本文认为直流磁化曲线就是交直流共同作用下的磁化曲线。当仿真计算直流偏磁设备时，可以用直流磁化曲线描述硅钢片材料的直流偏磁性能，无需计算出交直流共同作用下的磁化曲线，这样既无需直流偏磁下的磁特性测量设备，也减少了计算的工作量。

鉴于目前在变压器直流偏磁问题的仿真计算中，标准条件下的交流磁化曲线和平均磁化曲线仍被广泛使用的实际情况，本文以变压器制造企业提供的容量为160/80kV·A 干式变压器为研究对象，讨论直流磁化曲线、交流磁化曲线和平均磁化曲线对磁场仿真结果的影响。

3 直流偏磁变压器模型仿真计算与实验验证

3.1 模型结构

图7 给出了两台D-160/2 型变压器，实验时利用自行设计的外电路使该变压器工作在直流偏磁条件下。该变压器铁心采用步进搭接的叠片方式，叠片系数为0.96，铁心材料为30ZH120。变压器线圈参数见表。

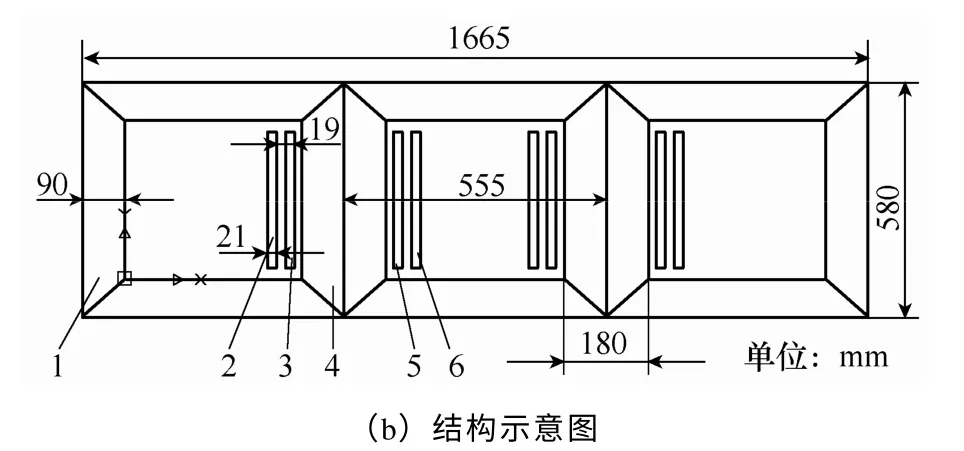
图7 干式变压器模型1—旁轭 2—高压绕组 3—低压绕组 4—铁心柱5—低压绕组 6—高压绕组Fig.7 Dry-type transformer model

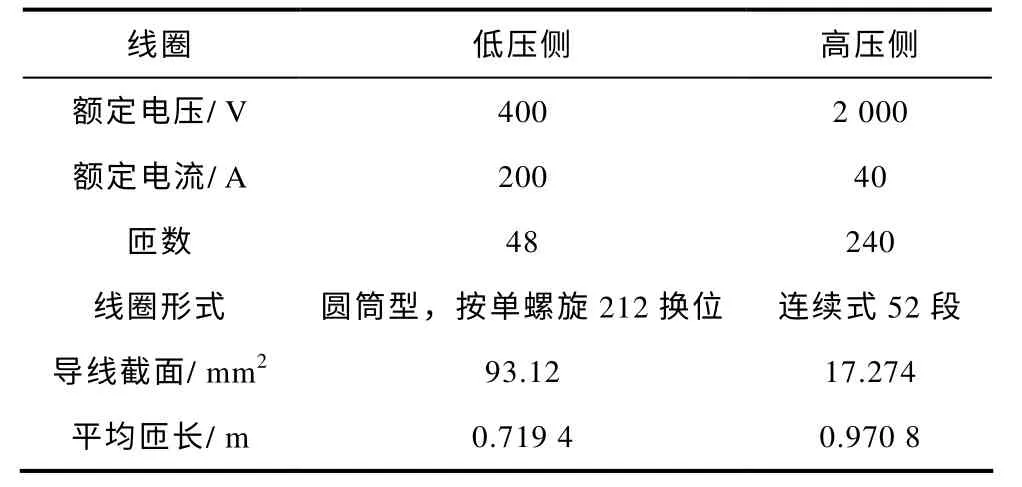
表 变压器线圈参数Tab. Transformer coil parameters

3.2 实验测试

试验时外接电路如图8 所示，采用的设备有单相交流电源、单相调压器、隔离变压器、直流电压源和功率分析仪等。其中两台干式变压器一次侧并联，二次侧反向串联并加入扼流圈，作用是消除一次交流电压对二次电路的影响。

图8 实验电路Fig.8 The electrical circuit for test

试验时，变压器工作在空载状态，一次侧通过调压器输入400V 的额定电压；二次侧相当于直流绕组，直流电流的大小通过滑动变阻器调节。空载损耗由功率分析仪测得。本文测定了直流电流依次为0.37A、1.02A、1.6A 时的空载损耗。

3.3 三维仿真计算及与实验结果对比分析

下面将对第3.2 节描述的变压器工况进行仿真计算。采用加拿大Infolytica 公司的Magnet 磁场仿真软件进行三维场路耦合瞬态有限元分析[4,13]。考虑到空载运行时漏磁场很小，因此三维建型时忽略变压器拉板、夹件等结构件。

仿真计算时，一次电压和二次直流电流通过场路耦合的外电路分别加到一次、二次绕组的场计算单元，电路连接如图9 所示。计算了铁心材料选取不同磁化曲线时，在直流偏磁电流依次为0.37A、1.02A、1.6A 时的铁心磁场分布及损耗。图10 给出了偏磁电流为0.37A、铁心磁特性用交流磁化曲线描述时磁通密度的分布云图。

图9 电路连接图Fig.9 Circuit connection diagram

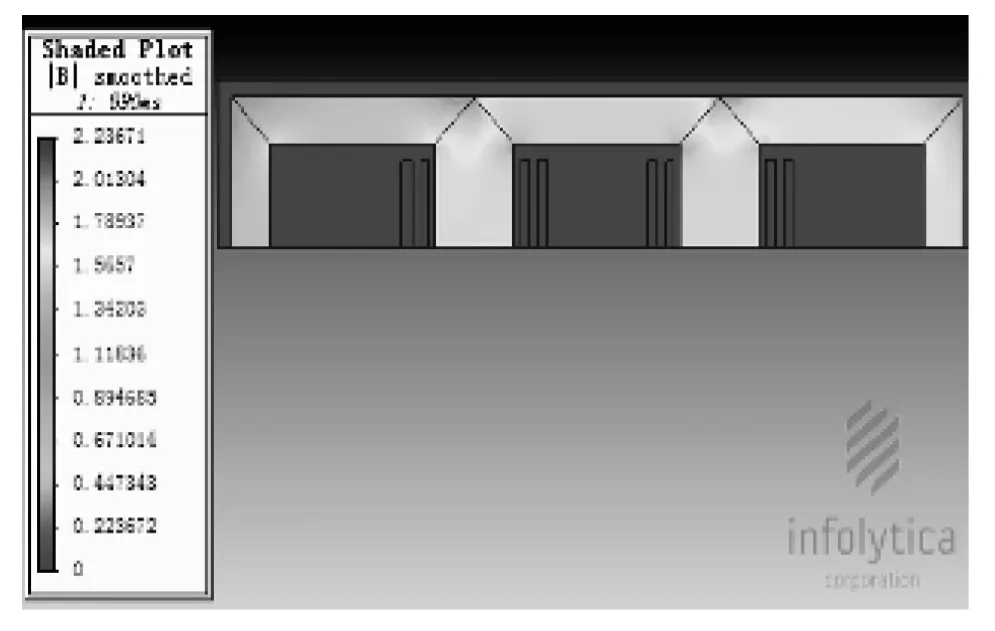
图10 偏磁电流为0.37A 时变压器磁密分布图Fig.10 Magnetic flux density distribution with DC bias current of 0.37A

图11 给出了仿真结果与实验测试结果的对比情况。从对比数据可以看出，随着偏磁电流的增加，3 种磁化曲线的仿真损耗与实测损耗的偏差逐渐加大。相对而言，直流磁化曲线的计算结果最接近于实测值，相对误差在2%左右，而交流磁化曲线和平均磁化曲线计算的损耗误差较大，最大相对误差达到10%。这也验证了上面第2 节的结论，即仿真计算直流偏磁电工设备时，可以用直流磁化曲线描述硅钢片材料的磁性能。

图11 损耗仿真结果与实测结果的对比Fig.11 Comparison of loss simulation results with experimental ones

4 结论

本文利用爱泼斯坦方圈法测量了有、无偏磁条件下硅钢片材料的磁化特性，阐述了三种不同磁化曲线的定义方式及提取方法。对变压器制造公司提供的两台完全一样的实际变压器进行了直流偏磁空载实验，并利用Magnet 商用软件对该模型进行了场路耦合瞬态场仿真的对比研究。研究表明，交直流共同作用下的磁化曲线在数值上实际与直流磁化曲线属于同一条磁化曲线，这样既无需直流偏磁下的磁特性测量设备，也减少了计算的工作量；在直流偏磁设备的电磁场数值计算中，采用直流磁化曲线描述材料偏磁特性的损耗计算结果相对于交流磁化曲线和平均磁化曲线更接近实测值。

[1]Yao Yingying,Chang Seop Koh,Ni Guangzheng,et al.3-D nonlinear transient eddy current calculation of online power transformer under DC bias[J].IEEE Transactions on Magnetics,2005,41(5):1840-1843.

[2]赵志刚.电力变压器直流偏磁问题的工程模拟[D].天津:河北工业大学,2010.

[3]赵小军.基于谐波平衡有限元法的变压器直流偏磁特性研究[D].北京:华北电力大学,2011.

[4]程志光,高桥则雄,博扎德·弗甘尼.电气工程电磁热场模拟和应用[M].北京:科学出版社,2008.

[5]郭满生,梅桂华,张喜乐,等.直流偏磁条件下单相三柱电力变压器损耗计算[J].电工技术学报,2010,25(7):67-71.Guo Mansheng,Mei Guihua,Zhang Xile,et al.calculation of losses in single phase three limb transformer under DC-biasing[J].Transactions of China Electrotechnical Society,2010,25(7):67-71.

[6]赵志刚,刘福贵,程志光,等.HVDC 中直流偏磁电力变压器叠片铁心损耗及磁通分布[J].高电压技术,2010,36(9):2346-2351.Zhao Zhigang,Liu Fugui,Cheng Zhiguang,et al.Loss and flux distribution of power transformers laminated core under DC-biased magnetization condition in HVDC[J].High Voltage Engineering,2010,36(9):2346-2351.

[7]郭满生,梅桂华,刘东升,等.直流偏磁条件下电力变压器铁心B-H 曲线及非对称励磁电流[J].电工技术学报,2009,24(5):46-51,59.Guo Mansheng,Mei Guihua,Liu Dongsheng,et al.B-H curve based on core and asymmetric magnetizing current in DC-biased transformer[J].Transactions of China Electrotechnical Society,2009,24(5):46-51,59.

[8]梅文余.动态磁性测量[M].北京:机械工业出版社,1985.

[9]Kaimori H,kameari A,Fujiwara K,et al.FEM computation of magnetic field and iron loss in laminated iron core using homogenization method[J].IEEE Transactions on Magnetics,2007,43(4):1405-1408.

[10]刘硕.磁场数值计算中材料特性模型的研究[D].天津:河北工业大学,2000.

[11]曹华贵.爱泼斯坦方圈测电工钢片直流偏磁性能方法研究[J].中国制造业信息化,2009,38(11):40-43.Cao Huagui.Research on the magnetic properties of electric steel sheet with DC magnetic field based on epstein frame[J].Manufacture Information Engineering of China,2009,38(11):40-43.

[12]Takaki Yamamoto,Yoshihiro Ohya.Single sheet tester for measuring core losses and permeabilities in a silicon steel sheet[J].IEEE Transactions on Magnetics,1974,MAG-10(2):157-159.

[13]谢德馨,杨仕友.工程电磁场数值分析与综合[M].北京:机械工业出版社,2009.