非磁饱和偏置下自传感主动电磁轴承的转子位移协同估计

唐 明 祝长生 于 洁

（1.浙江大学电气工程学院 杭州 310027 2.国网四川省电力公司电力科学研究院 成都 610072）

1 引言

主动电磁轴承（以下简称电磁轴承）系统采用可控电磁力来支承转子，由于没有机械接触而使其具有无机械磨损、无需润滑、低损耗等优良特性，这些特性使得电磁轴承具有在真空、低温等极端环境和高速旋转机械、航空航天等领域广泛应用的潜力，是融多学科复杂的机电一体化系统[1,2]。电磁轴承系统通常由控制器、功率放大器、电磁轴承本体、位移传感器等部件组成。位移传感器作为系统唯一的反馈部件却由于体积不够小而无法安装到轴承内部，因此引起测得位移与转子位移不同位等问题。对于刚性转子，不同位问题可以通过三角换算来近似估计转子位移；对于柔性转子，不同位问题所引起的位移测算则要复杂很多。而且，位移传感器通常价格较为昂贵，阻碍了电磁轴承的推广和产业化。因此，对于电磁轴承无位移传感器运行（又称自传感运行）的研究迫在眉睫。

实现电磁轴承自传感运行的方法通常有两种[3]：一种是基于现代控制理论的状态观测法；另一种是基于电感测量的参数估计法。状态观测法将电磁轴承系统视为一个双口网络，以电磁轴承的系统参数为依据设计相应的状态观测器，通过测量电压、电流来观测转子的位移从而实现反馈控制。Vischer和Bleuler 等[4]详细分析了此类方法的原理以及可行性，并使用该方法实现了系统的稳定悬浮，该方法原理清晰实现简单，不足之处在于容易受到电磁轴承系统参数变动的影响，鲁棒性较差。对于参数估计法[5-7]，原理是利用电磁轴承绕组的电感属性，因为绕组的等效电感是定转子之间气隙的函数（成近似的反比关系），因此可以通过测量对应方向上绕组的等效电感来估测该方向上的气隙长度，或者直接以检测到的电磁轴承各线圈的电感值为反馈量，进行反馈控制[8]，从而实现电磁轴承系统的无传感器运行。对于采用线性功率放大器的电磁轴承系统，通常使用高频小信号注入法来检测电磁轴承各线圈的等效电感值[9-11]；对于采用高频开关功率放大器的电磁轴承系统，PWM 开关信号本身就是一种高频信号源，电磁轴承各线圈的电感可以采用信号解调的方法从各线圈的电压、电流信号解调出[12,13]，Noh[14]，Dominick[15]分别在各自的博士论文中详细阐述并成功使用电感估计法实现自传感电磁轴承系统的稳定悬浮。

无论何种自传感检测位移的方法，其本质都是对线圈绕组的等效电感进行测量和估计。而电感本身只有在磁场没有饱和的情况下，才与气隙成近似的反比关系。一旦磁场进入饱和区，绕组线圈的等效电感将急剧减小。因此，当电磁轴承工作于磁场饱和区域时，即使是瞬时性的，也有可能由于气隙估计的反向性导致错误的位移估计，从而引发正反馈，造成整个系统的失稳、甚至崩溃。Lyons 等[16]在定子上设计了更多的磁极，采用马蹄形六对极结构。基于该结构，在所选择的磁极对上瞬间减小磁通密度以保证离开饱和点一个固定值。然后，在这对磁极中加入电流摄动去估测气隙大小。该方法的主要缺点是要求功放电压快速地为这对磁极去饱和，这已经超出了系统的通常要求。Skricka 等[17]则详细分析了饱和与耦合等效应对位移估计带来的干扰，从补偿的角度出发，对估测得到的位移进行了修正。该方法的主要缺点在于要求对实物各项参数甚至磁饱和曲线的精确获取。

通常，电磁轴承系统较多的采用恒定偏置加差动控制策略，即在一定的偏置磁通密度下，相对磁极的控制电流、电压此消彼长。在气隙变换频率远低于电流变换频率这一大前提下，可以认为相对磁极的磁通密度也是此消彼长的。只要偏置磁通密度不选在饱和点附近，即非饱和偏置，则相对磁极必定不会同时处在饱和情况下，这就为气隙长度的正确估计提供了可能性。在此非饱和偏置的情况下，一对相对磁极中必有磁通密度未饱和的绕组，其等效电感和气隙的对应关系依然遵循近似的反比关系，可以利用该未饱和绕组进行气隙估测。另外，在两个相对磁极均未饱和的情况下，两端绕组对气隙的估测也可以用来进一步提高位移估计的精度和信噪比。

本文从自传感电磁轴承的电感模型出发，推导出绕组等效电感与对应定转子气隙的函数关系式，在此基础上讨论了磁场饱和对电感和气隙估测的不利影响。针对这一问题，首次提出了相对磁极协同位移估计策略，并在四自由度径向电磁轴承系统平台上对该策略进行了测试与验证。实验结果表明：本文提出的相对磁极协同位移估计策略，能够有效地拓宽自传感电磁轴承运行的电磁条件，间接的为系统刚度的增大提供了基础，增强了系统的鲁棒性。

2 电磁轴承的电感模型与位移估计方法

8 极电磁轴承的定子实物图和绕线图分别如图1 所示。从电路的角度上讲，电磁轴承的绕组线圈也与电机一样，相当于感性负载。研究绕组的等效电感与该绕组对应的定转子气隙间的函数关系式是进行无位移传感器控制的基础。

图1 8 极电磁轴承定子实物图Fig.1 8-pole stator of magnetic bearing

取垂直正方向的绕组为研究对象进行建模分析，定转子电磁回路示意图如图2 所示。图2 中，V为绕组两端的电压，I为绕组线圈中的电流，x为定转子之间的气隙长度，lc为定转子内部的磁场回路的平均长度，N为绕组匝数（每个极靴上各绕N/2匝）。由于该示意图为平面图，故未能将极靴面积A绘于其中。

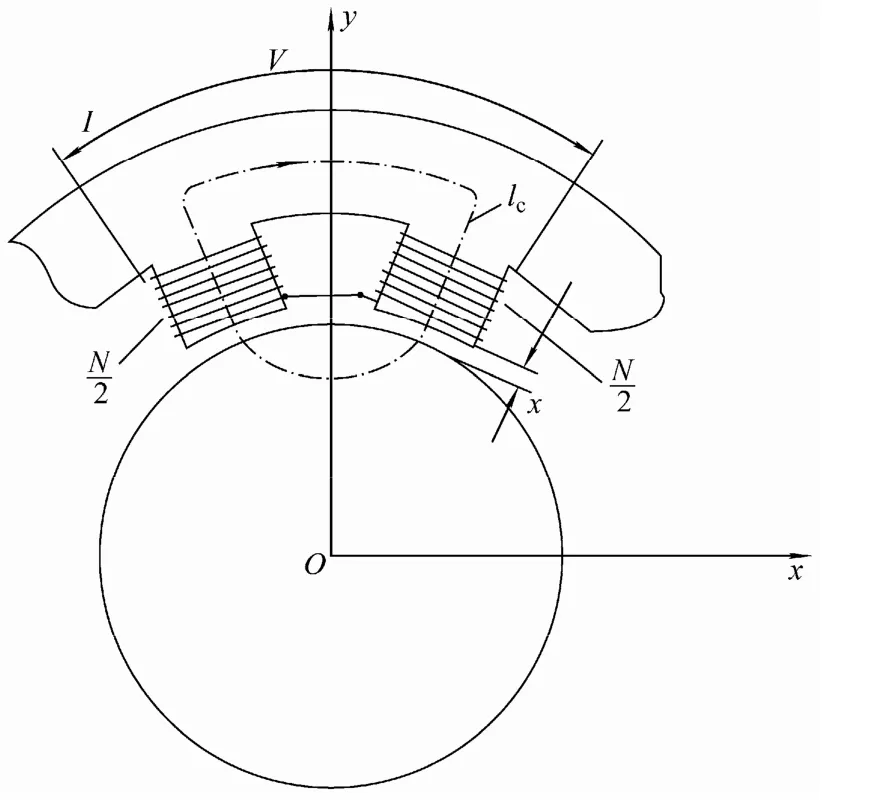
图2 定转子电磁回路示意图Fig.2 Demonstration of electromagnetic loop of stator and rotor

电磁轴承一相绕组的电压方程为

式中Φ——忽略漏磁通条件下的主磁路中的磁通量；

R——线圈电阻。

主磁通可以由下式表示

式中Rm——磁场回路的总磁阻，可由下式计算其中

μ0——空气的磁导率；

μr——铁磁材料的相对磁导率。

线圈中的主磁链为

由式（2）～式（4）可得，线圈绕组的等效电感L为

式中，lc/μr可以理解为将定、转子磁路等效为一段气隙，在定转子铁磁材料内部磁场没有进入饱和区时，μr通常很大，等效气隙项lc/μr与2x相比要小至少一个数量级，可以忽略[18,19]。忽略之后，绕组等效电感与其对应气隙长度可以看做成近似的反比函数关系，这也就是电感法测量气隙长度的理论依据。

电感测量的一般方法是对待测线圈通入恒频恒幅的激励信号源，通过提取线圈两端对应频率下电压和电流信号的幅值来计算其感抗，进而获得其电感量。在采用开关功率放大器作为驱动的电磁轴承系统中，则主要利用PWM 信号的高频特性进行电感的测量。测量方法不同于一般的小信号注入法，以电流型恒频开关功率放大器为例：电磁轴承线圈两端的电压V(t)的时域表达式为

式中Ts——开关周期，Ts=1/fs；

fs——开关频率；

αk——第k个开关周期的占空比。

将上式展成傅里叶级数的形式为

对于纯感性负载，电流信号的表达式为

式（8）中的无穷级数项即为由PWM 开关信号所引起的电流纹波，且其各阶谐波的幅值随阶次的增加而迅速衰减。为了提高信噪比，实验中只提取电流纹波信号的基频分量i1(t)，即n=1。由式（8）可得

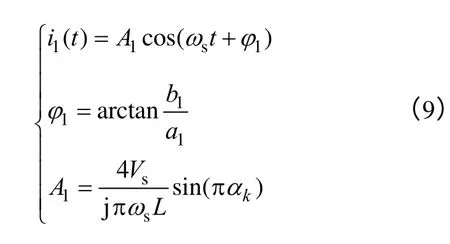
从频域的角度，式（9）中A1可以看做电流信号纹波基频分量i1(t)的幅值。实验中，将电流信号通过高通滤波器、绝对值电路、低通滤波等一系列信号调理的环节可以提取i1(t)的幅值A1。将PWM信号经过电平匹配送入DSP28335 的eCAP 口可以捕获实时的占空比信号αk，式（9）可以获得此时绕组的等效电感L。

将电感表达式（5）代入式（9）可以进一步得到

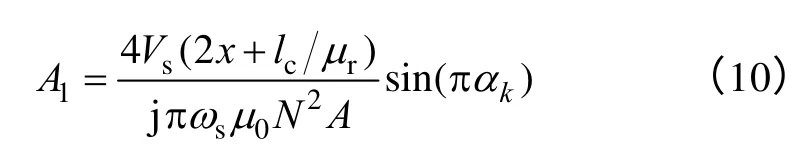
将式（10）写成如下形式

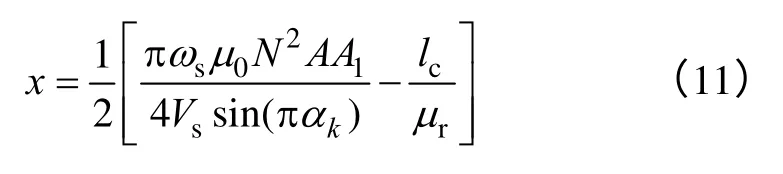
在定转子铁磁材料未饱和的情况下，等效气隙lc/μr小到可以忽略，气隙长度x可以通过测得的A1与αk经由式（11）直接算出。但是当定转子铁磁材料内的磁场进入饱和区之后，lc/μr数值急剧增大，不可忽略，由上式计算得到的位移不能作为系统反馈。

3 磁饱和对电感、位移估计的影响

电磁轴承系统一对磁极所能产生的电磁力F为

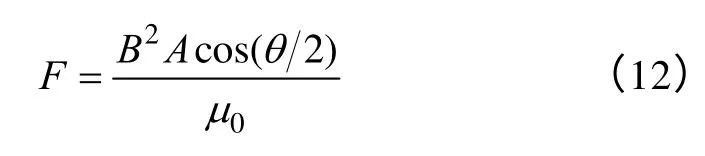
式中θ——该对磁极的中心线夹角；

B——磁极处气隙中的磁感应强度，可以写为

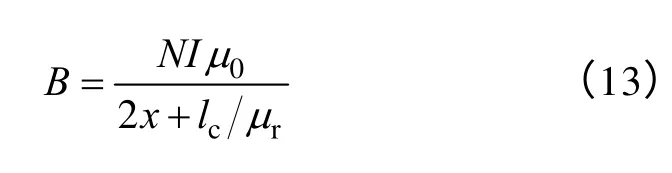
由式（12）、式（13）可知，要提高电磁轴承的电磁力只能通过增大磁极线圈中的电流I来增大气隙中的磁感应强度B。在电磁轴承系统遇到幅值较大或者频率较高的外力扰动时，控制器会响应出较大的瞬时电流，因此容易在某些磁极中产生短时间的磁场饱和现象。磁饱和后，相对磁导率μr急剧减小，等效气隙lc/μr的数值甚至可以淹没原本气隙长度x的变化。由式（5），饱和情况下的绕组等效电感也将因lc/μr的增大而减小，电感值的变化也不再单调的反应气隙长度x的变化，此时通过电压电流信号所测得的绕组等效电感已经毫无意义。

使用Ansoft-Maxwell 软件对定转子进行建模。通入不同的励磁电流，给定不同的定转子气隙，有限元法对等效电感计算的结果如图3 所示，据此电感所估计的气隙长度如图4 所示。

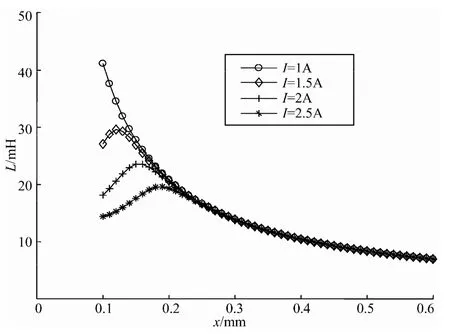
图3 不同绕组电流下等效电感随气隙长度的变化Fig.3 Variation of equivalent inductance with air gap under different coil currents

图4 不同绕组电流下的位移估计值Fig.4 Position estimation under different coil currents

由图3和图4 可见，在磁场未进入饱和区时，电感的大小主要取决于气隙长度，与电流无关，是气隙长度的单调函数。饱和之后，尤其是在气隙较小的深度饱和区，同一个测得的电感，可能对应着两个不同的转子位置。这种情况下，极易造成系统的失稳甚至崩溃。

4 相对磁极协同位移估计策略

4.1 相对磁极协同位移估计策略结构

图5 所示为自传感电磁轴承系统单自由度的差动控制框图及双绕组协同位移估计策略的结构。控制器以位移估计值xest为位置反馈，通过计算输出控制电流ic。再与偏置电流ib进行运算，得到相对绕组各自的电流给定：i1=ib+ic；i2=ib-ic；i1，i2经过电流型功率放大器，驱动相应的电磁轴承线圈，产生电磁力对转子位置进行主动控制。

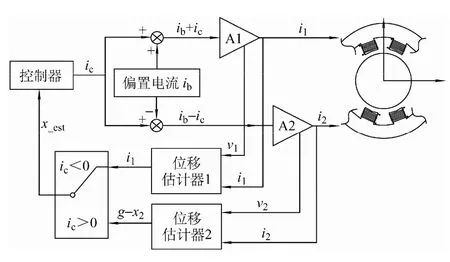
图5 双绕组协同位移估计策略Fig.5 Position estimation strategy using both pole pairs

相对磁极线圈绕组各自的电压、电流信号v1、v2、i1、i2分别通过两路相同的位移估计器，解调出对应的气隙值x1、x2。在两个相对磁极都未饱和的情况下有：x1+x2=g，其中g为气隙的总长度。决策器的作用主要是选择未饱和绕组。决策逻辑为：当控制电流ic＜0 时，选择x1作为反馈量；当控制电流ic＞0 时，选择x2，由g-x2作为反馈量。决策器的控制逻辑就是选相对磁极中电流较小的绕组线圈所估计的位移进入控制器。当偏置电流ib选为无饱和偏置电流时，则可以确保相对磁极中电流较小的一端远离磁饱和区。

4.2 无饱和最大偏置电流的论证

偏置电流的作用主要用来产生一定的偏置磁通，由于电磁轴承本身的非线性特质，建模时在其工作点附近进行了线性化，必要的偏置磁通，可以降低模型的非线性度、增大系统的等效刚度、提高电磁力的响应速度[20]，进而增强系统的稳定性。

但是对于无传感器电磁轴承来说，偏置电流的选取则需要考虑可能发生的磁饱和现象。在差动控制的大前提下，为了达到总有一端磁极处于非磁饱和态，必须考虑到可能发生的一些极易造成磁饱和的工况，例如脉冲或阶跃式外力扰动。

由式（13）易知，磁饱和现象最容易发生在小气隙和大电流的场合，因此对磁饱和现象的规避也应该从这两方面进行考虑。本文设计决策器初衷即是从电流方面对磁饱和现象进行规避，但电流较小的绕组还是可能会因为气隙太小而出现磁饱和现象。电磁轴承系统中，保护轴承的存在限制了定转子之间的气隙，本实验平台中气隙范围是：0.1～0.6mm。也就是说，在电流较小的那一绕组方面，只要能确保当气隙在0.1mm 时不发生饱和现象，也就保证了其他所有情况下都不会发生磁饱和现象。

在最小气隙的情况下，逐渐增大绕组电流直到临近磁化曲线的拐点附近，此时的电流即为无饱和偏置电流的最大值ibmax。磁通密度的测量可以通过在定转子之间的微小气隙内埋置纤薄型的磁通传感器来测量磁场是否饱和，但更简易更合理的办法是观测电流信号的高频纹波。

4.3 无饱和偏置电流最大值的实验测定方法

在恒频电流型开关功率放大器的驱动下，线圈绕组电流的纹波波形为高频三角波，该三角波的峰峰值直接反应了感性负载的电感值，从而间接反应了气隙的大小。在磁场没有饱和的时候，如果气隙恒定，则三角波的峰峰值是不会改变的。基于此种特性，无饱和偏置电流的最大值ibmax可以通过如下实验方法进行测定：对相对磁极的某一端通入一恒定直流电流，转子受到电磁力的吸引作用，必定紧紧的靠在保护轴承上（选择重力方向最方便）。此时，该通电磁极下定转子间的气隙长度即为气隙取值范围中的最小值xmin，改变恒定直流电流的大小，同时通过示波器观察电流纹波的峰峰值，如前所述，在磁场未达到饱和的时候该峰峰值不会改变。不断增大通电磁极的电流，直到电流纹波的峰峰值不再维持恒定反而开始增大。此时的电流值即为实验测定的无饱和偏置电流最大值ibmax。实验平台中测得的无饱和偏置电流最大值约为ibmax=1.2A。

5 实验结果

5.1 四自由度径向电磁轴承实验平台

四自由度径向电磁轴承实验平台（见图6）主要包括：电流型恒频功率放大器、TMS320F28335控制核心板、DL1620 数字示波器、A02—7112 型异步电机、木槌、四自由度径向电磁轴承、PC 上位机。系统平台的主要参数见下表。

表 四自由度径向电磁轴承系统平台主要参数Tab.Main parameters of 4-DOF experimental platform

图6 四自由度电磁轴承实验平台Fig.6 4-DOF experimental platform of AMBs

5.2 单自由度静态磁饱和实验

将三相异步电机与AMB 转子的连接暂时脱开，启动系统，进行无传感器的静态悬浮。在转子稳定悬浮后，使用木槌在垂直方向向下用力敲击转子，则上线圈的电流必定陡然增大，以此来制造上线圈中短暂的磁场饱和现象。

图7 所示为左侧电磁轴承起动过程与敲击前后上下线圈的电流信号。电磁轴承的启动过渡过程约在0.03s 之后完成。木槌向下敲击之后，上线圈电流陡然增大，最大值约在4.5A 附近。下线圈电流受限最小自传感电流（实验中设定为0.5A），一直维持0.5A 的电流。经过约0.03s 的调整后各自重新步入稳态。图8 所示为上下线圈各自位移估计器输出的位移信号。

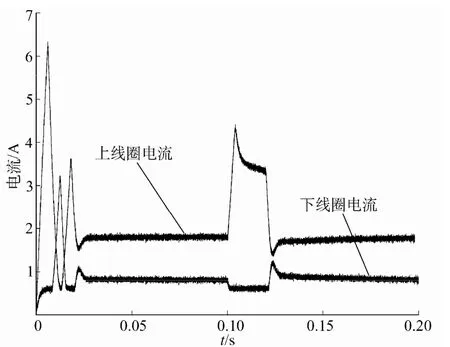
图7 左侧电磁轴承上下线圈敲击后的电流响应Fig.7 Current waveforms in the opposing coils of left AMB after being tapped by the mallet

图8 上下线圈各自位移估计器的输出对比Fig.8 Estimator output of the opposing coils

将定转子几何中心线重合的位置定义为坐标零点，受限于保护轴承，转子的位移范围应为：[-0.25mm,0.25mm]，气隙的取值范围为：[0.1mm，0.6mm]。实验为了用尽量小的电流制造出磁场饱和现象，将转子垂直方向的位移给定从零点上调至0.1mm。图8 中上下线圈位移估计的输出在整个0.2s的过程中几乎完全一致，只有在木槌敲击后的短暂时刻里（图中画圈的部分）产生了差异，这也正是饱和所致。但此时ic＞0，决策器将忽略上线圈的位移估计，采用下线圈的位移估计值进行反馈，成功的避免了由磁饱和带来的位移估计误差，系统依旧能稳定运行。

5.3 四自由度全系统旋转实验

为了进一步验证所提出的相对磁极协同位移估计策略的有效性和优越性，在四自由度电磁轴承系统平台上进行了不同转速下的悬浮对比实验。实验中，左侧AMB 每个自由度只采用单个线圈绕组进行位移估计，右侧AMB 采用相对磁极线圈绕组进行协同位移估计，将两个轴承中转子的位移轨迹在不同转速下进行对比，如图9 所示（单位mm）。

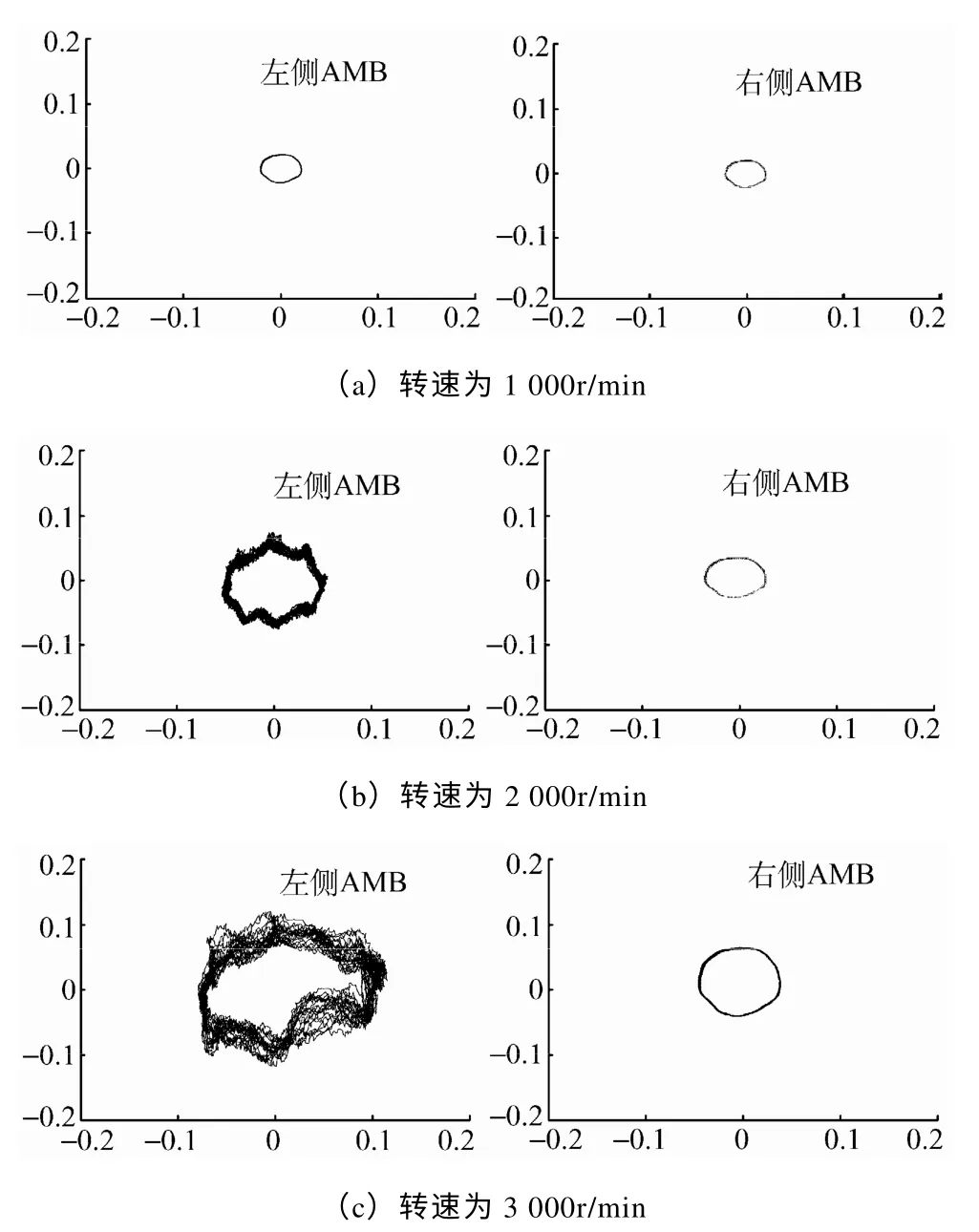
图9 不同转速下左右AMB 内转子的轨迹Fig.9 Rotor trajectory in both AMBs under different speeds

由于转子自身的质量不平衡特性，使得其与转速同频的振动量的幅值随转速的增大而增大。控制器为了维持系统的稳定，控制电流的变化幅度也将随转速的增大而增大。因此，当转速较低时，同频振动幅值不大，绕组电流较小，几乎没有饱和出现；当转速较高的时，同频振幅变大，绕组电流随之增大，容易出现饱和现象。实验中，可以通过调整配重盘的参数，来改变转子的不平衡量。图9 中，转速为1 000r/min 时，左右AMB 中转子轨迹无明显差别。当转速为2 000r/min 时，左右AMB 已经有明显差异，左侧转子轨迹较杂乱，但轨迹整体幅度与右侧AMB 中转子轨迹相当。此时属略微饱和，系统尚能保持稳定。当转速达到3 000r/min 时，左侧AMB 中转子位移轨迹已经趋于失稳，而采用协同位移估计策略的右侧AMB 中转子轨迹幅度只是略有增大。

将左右AMB 均配置成协同位移估计策略，整个系统由1 500r/min 加速至3 000r/min 过程中的转子轨迹（左右基本一致）如图10 所示。在加速过程中，受扰于异步电机的切向电磁力，转子轨迹略微杂乱。

图10 转子由1 500r/min 至3 000r/min 加速轨迹Fig.10 Rotor acceleration trajectory from 1 500 r/min to 3 000 r/min

旋转实验证明，采用非饱和偏置下的相对磁极协同位移估计策略能够有效的避免某一磁极的短暂饱和给位移提取带来的误差，从而提高系统的抗干扰能力及稳定性。

6 结论

针对电磁轴承运行中可能出现的磁饱和现象，建立了电磁轴承的电感模型，讨论了磁饱和现象对电磁轴承绕组的等效电感和位移估计的影响，及其对整个电磁轴承系统可能带来的致命危害。利用在非饱和偏置磁通的条件下必有一端绕组处在非饱和状态的原理，提出一种利用相对磁极的线圈绕组进行协同估计的双绕组位移提取策略，拓展了无传感器条件下电磁轴承系统运行的条件，提高了系统的静态承载力范围，从而间接提高了系统的鲁棒性。静态饱和测试与四自由度电磁轴承系统 0～3 000r/min的实验充分验证了所提策略的正确性和可行性。

[1]Bleuler H.Survey of magnetic levitation and magnetic bearing types[J].JSME International Journal,Series 3:Vibration,Control Engineering,Engineering for Industry,1992,35(3):335-342.

[2]Vischer D.Sensorlose und spannugsgesteuerte magnetlager[M].Zurich,Switzerland:Swiss Federal Institution Technology,1988.

[3]Maslen E H.Self-sensing for active magnetic bearings:overview and status[C].Proceedings of the 10th Internation Symposium on Magnetic Bearings,2006:10-15.

[4]Vischer D,Bleuler H.A new approach to sensorless and voltage controlled AMBs based on network theory concepts[C].Proceedings of the 2nd Internation Symposium on Magnetic Bearings,1990:301-306.

[5]Sivadasan K K.Analysis of self-sensing active magnetic bearings working on inductance measurement principle[J].IEEE Transactions on Magnetics,1996,32(2):329-334.

[6]Maslen E H,Iwasaki T,Mahmoodian R.Formal parameter estimation for self-sensing[C].Proceedings of the 10th International Symposium on Magnetic Bearings,2006:529-536.

[7]Hanson B,Levesley M.Self-sensing applications for electromagnetic actuators[J].Sensors and Actuators,A:Physical,2004,116(2):345-351.

[8]Hanson B M,Brown M D,Fisher J.Self sensing:closed-loop estimation for a linear electromagnetic actuator[C].Proceedings of the American Control Conference,2001:1650-1655.

[9]王军.无传感器磁悬浮轴承的研究[D].南京:南京航空航天大学,2005.

[10]Garcia P,Guerrero J M,EI Sayed I,et al.Carrier signal injection alternatives for sensorless control of active magnetic bearings[C].1st Symposium on Sensorless Control for Electrical Drives,2010:78-85.

[11]叶建民.自检测电磁轴承转子的位移检测研究[J].科技创业,2008(12):196-197.

[12]Mizuno T,Hirasawa Y.Self-sensing magnetic suspension using an H-bridge type hysteresis amplifier operating in two quadrants[C].IECON Proceedings on Industrial Electronics Conference,2002:1818-1823.

[13]Schammass A,Herzog R,Buhler P,et al.New results for self-sensing active magnetic bearings using modulation approach [J].IEEE Transactions on Control Systems Technology,2005,13(4):509-516.

[14]Noh D.Self-sensing magnetic bearings driven by a switching power amplifier[D].Virginia USA:University of Virginia,1997.

[15]Montie D T.Performance limitations and self-sensing magnetic bearings[D].Virginia USA :University of Virginia,2003.

[16]Lyons J P,MacMinn S R,Preston M A.Flux/current methods for SRM rotor position estimation[C].Proceedings of IEEE Industry Application Society Annual Meeting,1991:482-487.

[17]Skricka N,Markert R.Compensation of disturbances on self-sensing magnetic bearings caused by saturation and coordinate coupling[C].Proceedings of the 7th International Symposium on Magnetic Bearings,2000:165-170.

[18]Ranft E O,Gvan Schoor,du Rand C P.Self-sensing for electromagnetic actuators.part I:a coupled reluctance network model approach[J].Sensors and Actuators A:Physical,2011:400-409.

[19]Ranft E O,Schoor G van,Rand C P du.Self-sensing for electromagnetic actuators.part II:position estimation[J].Sensors and Actuators A:Physical,2011:410-419.

[20]张德魁,赵雷,赵鸿宾.电流响应速度及力响应速度对磁轴承系统性能的影响[J].清华大学学报(自然科学版),2001,41,(6):23-26.Zhang Dekui,Zhao Lei,Zhao Hongbin.Effect of current response rate and force response rate on performance of magnetic bearing systems[J].Journal of Tsinghua University,2001,41(6):23-26.