考虑开槽的分数槽集中绕组永磁同步电机电枢反应磁场解析计算

林 福 左曙光 马琮淦 谭钦文

（同济大学新能源汽车工程中心 上海 201804）

1 引言

分数槽集中绕组的每个线圈镶嵌在一个定子齿上，它有如下优点[1]：提高槽满率，增加功率密度；削弱谐波分量，改善反电动势波形的正弦性；减少线圈端部长度，各个线圈组端部没有重叠，不必设相同绝缘；便于使用专用绕线机，取代传统嵌线工艺，提高工效。总之，分数槽集中绕组有利于提高永磁同步电机的效率和功率密度，节约成本。然而，不同于整数槽集中绕组，分数槽集中绕组的排列方式比较复杂，不同极槽配合的电机绕组排列的规律不同，从而增加了其电枢反应磁场解析计算的难度。

为了得到较大的电动势和减少齿槽转矩，对于分数槽集中绕组单元电机的槽数Z0和极对数p0应尽量满足 Z0≈2p0，常见的三种极槽配合方式为Z0=2p0±1，Z0=2p0±2，Z0=2p0±4[2,3]。目前在国内，关于分数槽集中绕组产生的磁场的解析计算研究较少，文献[2]对三种不同极槽配合的单元电机的绕组系数进行计算，分析了各谐波成分所占的比例，但是它将单个线圈产生的磁场假设成为脉振矩形磁场，而且忽略了磁场在径向上的变化；文献[4]只对8 极9 槽的单元电机的绕组磁动势进行了计算，并没有提出统一的电枢反应磁场的解析表达式，而且文献[2,4]都未将开槽因素考虑在内，并且缺乏相应的验证。在国外，文献[5-7]通过求解二维极坐标下的拉普拉斯方程，并将开槽因素考虑在内，得到了考虑开槽的电枢反应磁场，解析计算的结果与有限元计算结果得到了很好的吻合，然而，它们也并没有针对分数槽集中绕组的分布规律提出统一的解析表达式。综上所述，由于分数槽集中绕组的分布方式复杂，鲜有文献对其产生的磁场提出一般的解析表达式，而且都未讨论开槽对电枢反应磁场的谐波成分和幅值的影响，因此，对于分数槽集中绕组永磁同步电机，有必要对电枢反应磁场的一般分布规律进行研究。

本文从单个线圈产生的磁场出发，针对三种常见的极槽配合方式，根据其磁场的空间分布矢量图，得到了电枢反应磁场的解析表达式，并通过复数气隙比磁导将开槽对电枢反应磁场的影响考虑在内，并且分析了考虑开槽的磁场的谐波成分，最后将解析计算的结果同有限元计算的结果进行对比。

2 单元电机电枢反应磁场

2.1 单个线圈产生的磁场

设原电机的相数为m，定子槽数为Z，永磁体极对数为p。若满足Z 和p 之间有最大公约数N0，且Z0=Z/N0为m 的整数倍，则原电机有N0个槽数为Z0极对数为p0的单元电机组成，原电机的电枢反应磁场可以看成单元电机磁场在空间上重复N0次。

为方便分析，作如下假设：

（1）铁心的磁导率为无穷大。

（2）忽略电机端部的影响。

（3）永磁材料磁导率与空气的相等。

分数槽集中绕组一个匝数为Ns的线圈，绕组的节距y=1，通入角频率为ω、最大值为I 的余弦交流电i(t)=Icos(ωt)。设α=0 处与线圈的中心重合，单个线圈的绕组磁场分布为[8]

式中，Bmμ是μ 次磁场分量的幅值，且

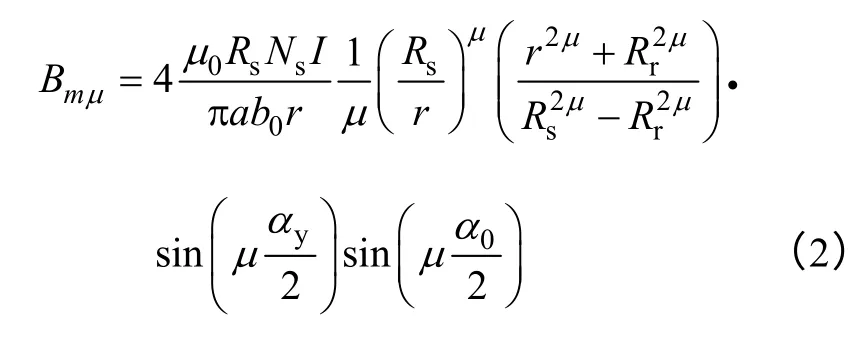
式中 μ0——真空磁导率；

Rs——定子半径；

a——并联支路数；

b0——槽口宽度；

r——所要求解处的半径；

Rr——转子半径；

αy——单元电机绕组节距，αy=2π/Z0；

α0=b0/Rs。

图1 所示为单个线圈产生的磁场分布，有些文献将单个线圈产生的磁场假设为脉振矩形磁场，显然这忽略了图中所示的突起部分和磁场沿径向上的差异，这对于感应电机等气隙较小的电机而言误差较小，而对于表贴式永磁电机，由于其有效气隙长度较大，需考虑磁场沿径向上的变化[9]。

图1 单个线圈产生的磁场Fig.1 The field produced by single coil

2.2 单元电机A 相绕组产生的磁场

单元电机的每极每相槽数q 为

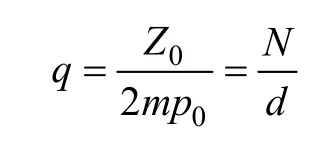
式中，N/d 是不可约的真分数。

电机通常按照60°相带划分相带，采用双层绕组时，N 是能够串联在一起组成1 个线圈组的线圈数。本文只对双层绕组进行分析。

由于不同极槽配合的的分数槽集中绕组，其排列形式不同[2,10]，下面分别对常见的 Z0=2p0±1，Z0=2p0±2，Z0=2p0±4 三种极槽配合的单元电机的电枢反应磁场进行分析。

2.2.1 Z0=2p0±1

N 为奇数，Z0为奇数，定子圆周被均分为3 个区间，每一个区间占2π/3 空间机械角度，三相各占据1 个区间。例如Z0=9，p0=4 或5 和Z0=15，p0=7或8，单元电机的线圈排列方式为AaABbBCcC 和AaAaABbBbBCcCcC，A 相绕组产生的磁场分布图如图2a 和图2b 所示。

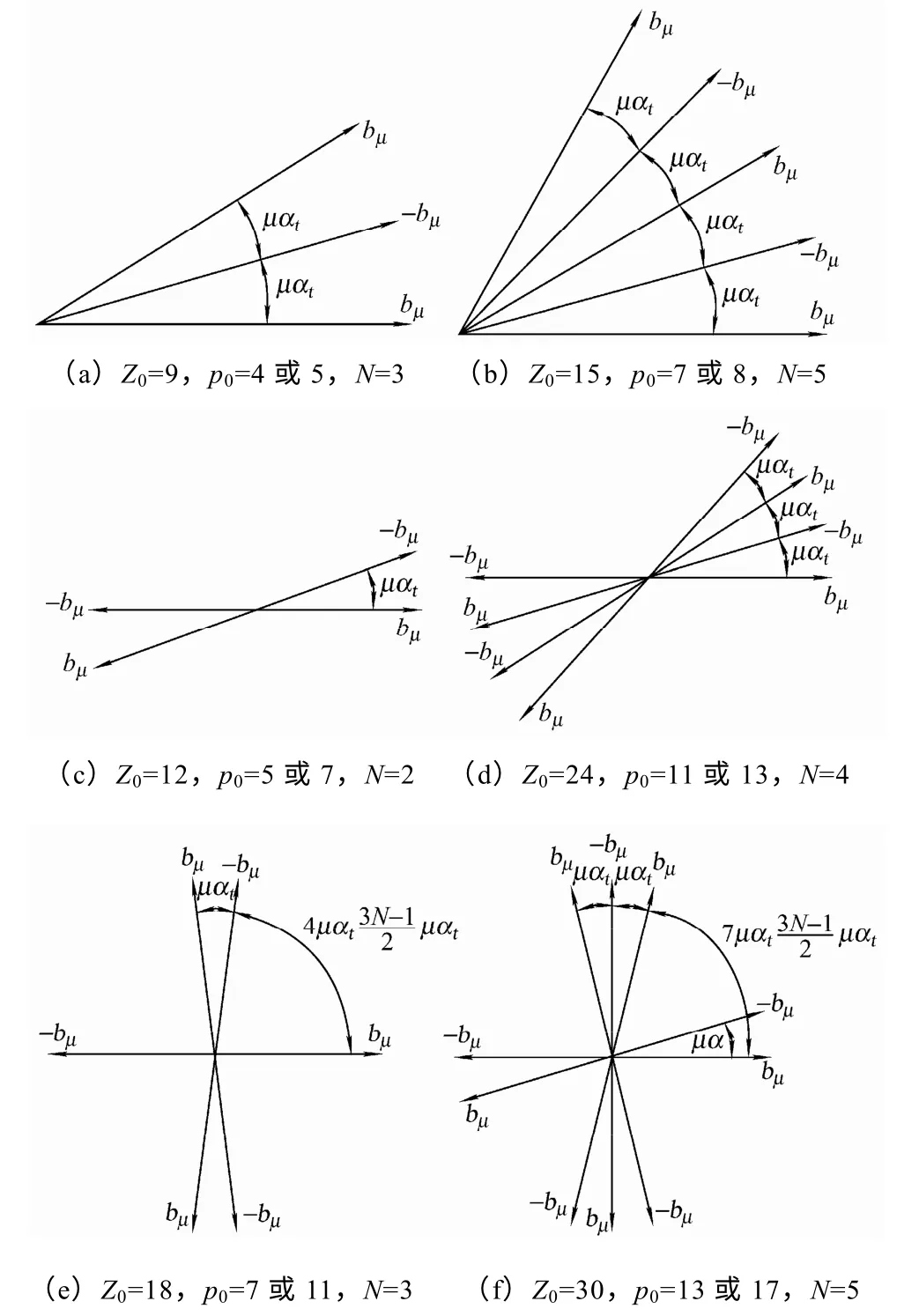
图2 A 相绕组磁场分布图Fig.2 Diagram of field produced by phase A winding

由图2 可得到单元电机A 相绕组产生的磁场为

式中，αt为单元电机相邻两个线圈的空间夹角，对于双层绕组，显然αt=αy=2π/Z0。

2.2.2 Z0=2p0±2

N 为偶数，Z0为偶数，定子圆周被均分为6 个区间，1 个区间占π/3。例如Z0=12，p0=5 或7 和Z0=24，p0=11或13的单元电机的线圈排列方式为AabBcCaABbcC和AaAabBbBCcCcaAaABbBbcCcC，A 相绕组产生的磁场分布矢量图如图2c 和图2d 所示。

从图2 得知，在一个圆周上，空间相差180°的两个线圈产生的磁场大小相等，方向相反，因而可认为单元电机A 相绕组产生的磁场认为由[0,π]和[π,2π]两部分磁场组成，且这两部分磁场大小相反，在空间上相差π。

[0,π]上的磁场为

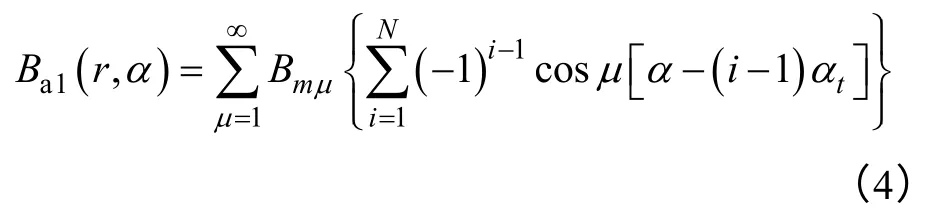
[π,2π]上的磁场为

因此单元电机A 相绕组产生的磁场为

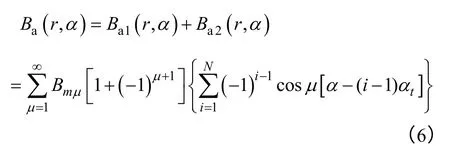
2.2.3 Z0=2p0±4

N 为奇数，Z0为偶数，N 个线圈不再连续分配同一个区间，被分为两部分，一部分有(N-1)/2 个线圈，一部分有(N+1)/2 个线圈。例如Z0=18，p0=7 或11 和Z0=30，p0=13 或17，单元电机的线圈排列方式为ABbcaABCcabBCAabc 和AabBbcCAaABbcCca-ABbBCcaAabBCcC，A 相绕组产生的磁场分布图如图2e 和图2f 所示。

同Z0=2p0±2 极槽配合下的绕组分布相同，该单元电机 A 相绕组产生的磁场也可以认为由[0,π]和[π,2π]两部分磁场组成，同样这两部分磁场大小相反，在空间上相差π。

[0,π]上的磁场为

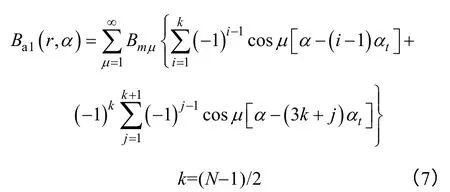
[π,2π]上的磁场为

因此单元电机A 相绕组产生的磁场为

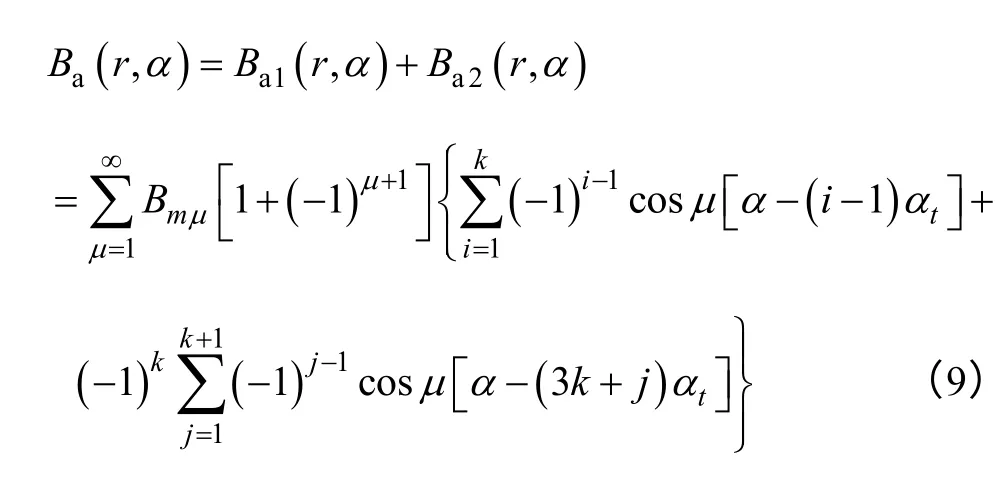
2.3 单元电机三相绕组的合成磁场

单元电机定子三相绕组等效轴线空间上彼此相差2π/3 机械角度。当对称的三相绕组通入时间上彼此相差2π/3 的对称三相交流电时，单元电机A、B、C 三相绕组合成磁场为

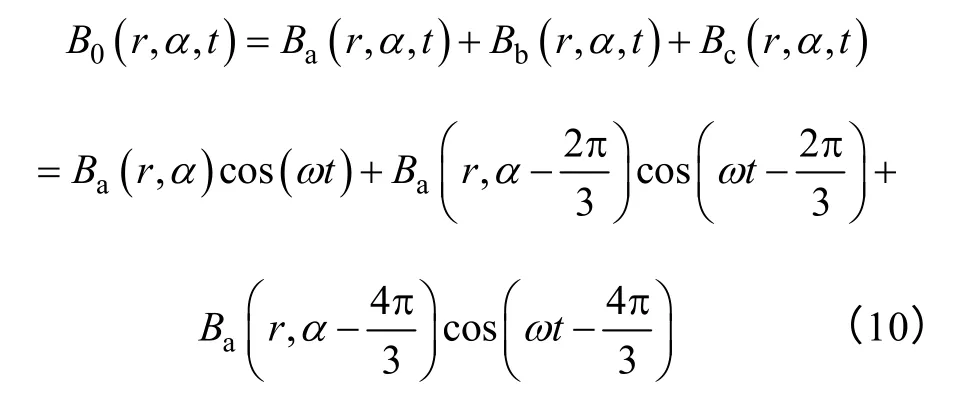
由式（3）、式（6）和式（9）可知单元电机的三相绕组产生的μ 次谐波磁场可表达成一般形式

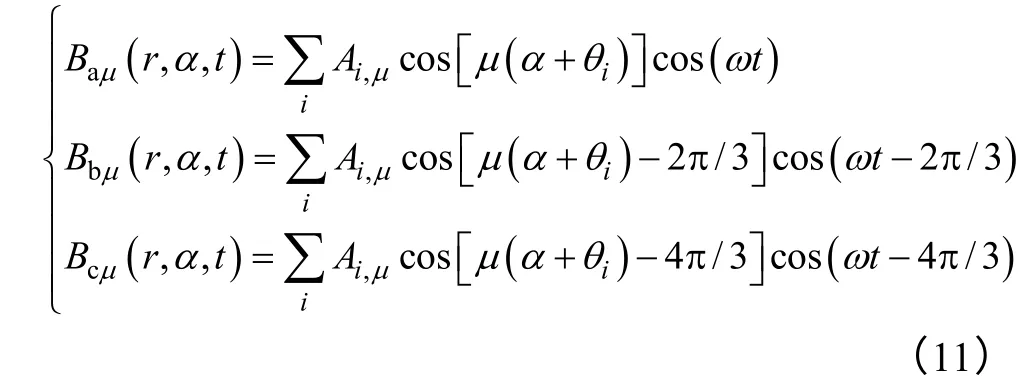
当μ 为3 的整数倍数时，单元电机的μ 次电枢反应磁场分量为

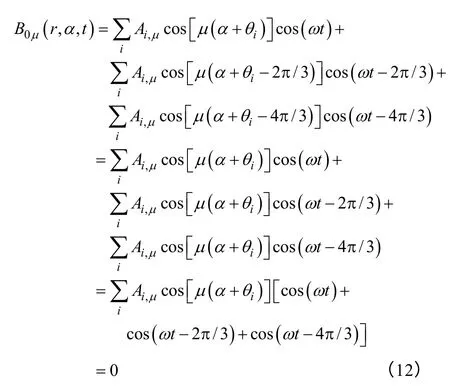
所以单元电机的电枢反应磁场不包含次数为3的整数倍的谐波成分。从式（6）和式（9）可以看出对于Z0=2p0±2 和Z0=2p0±4 的极槽配合的单元电机还不包含偶数次的谐波成分。

3 复数气隙比磁导

进入定子槽的磁场基本集中在槽口附近，所以可将实际的半开口槽用一无限深的径向开口槽代替，如图3 所示。图中，α1为定子槽下沿角度；α2为定子槽上沿角度；αs为定子槽距角。

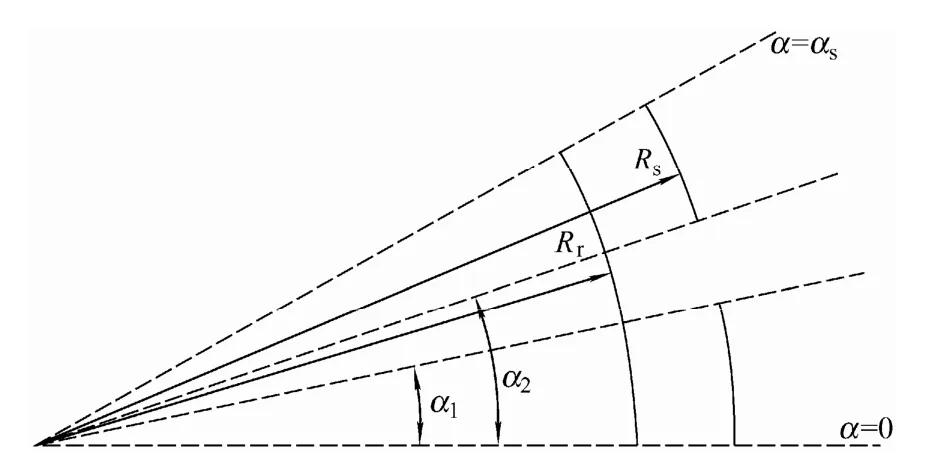
图3 S 平面的槽模型Fig.3 Slot model in the S plane

如图4 所示，通过4 组保角映射，把实际定子有齿槽变换为无齿槽进行分析，从而得到复数气隙比磁导。S 为变换前的实际有齿槽的坐标系；Z、W、T 为中间坐标系；K 为变换后的无齿槽的坐标系。坐标系之间按式（13）变换[11,12]。

图4 保角映射的基本步骤Fig.4 Basic steps of conformal mapping

由以上四组保角映射可得到复数气隙比磁导

由于切向磁场相对于径向而言较小，因此本文不考虑复数气隙比磁导的虚部，而只考虑其实部。可将比磁导实部表示成傅里叶级数形式

对于具有表1 参数的半闭口槽电机，其在永磁体表面处的一个槽距内的复数气隙比磁导的实部如图5 所示。

表1 电机主要结构参数Tab.1 Main parameters of PMSM

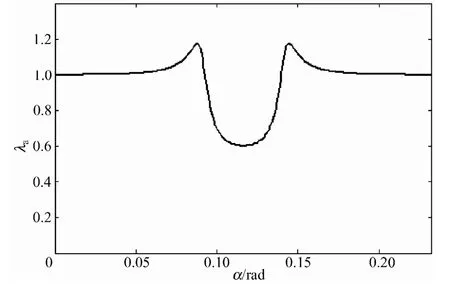
图5 一个槽距内的复数气隙比磁导的实部Fig.5 Real part of complex relative airgap permeance in one slot pitch

4 原电机的电枢反应磁场

由式（10）和式（15）可得到考虑开槽的原电机的电枢反应磁场为

原电机的电枢反应磁场在空间上表现为单元电机电枢反应磁场的重复，重复次数为单元电机个数N0。因此，原电机的电枢反应磁场不包含次数为N0μ(μ=3,6,9,…)的谐波成分；而且对于Z0=2p0±2 和Z0=2p0±4 的极槽配合的原电机还不包含次数为N0μ(μ=2,4,6,…)的谐波成分。

由式（15）和式（16）可知，开槽会引起次数为N0(μ±nZ0)的谐波成分。然而由前面的分析可知，电枢反应磁场的谐波次数μ 不为3 的整数倍，而Z0为3 的整数倍，所以(μ±nZ0)不为3 的整数倍，而且对于Z0=2p0±2 和Z0=2p0±4 极槽配合的原电机，Z0为偶数，由于μ 不为2 的整数倍，所以(μ±nZ0)不为2 的整数倍。因此，对于原电机而言，开槽并不会引起额外的谐波成分，而主要引起次数为N0(μ±nZ0)的谐波成分的幅值发生变化。

5 与有限元结果对比

本文借助有限元软件对表2 所示的12 对极27槽、14 对极24 槽、14 对极36 槽三种不同极槽配合方式的永磁同步电机的气隙中间处的电枢反应磁场分布进行计算，所取的线圈匝数为13，电流幅值为50A，将解析法计算的结果与有限元法计算的结果进行对比，如图6 所示。由图6 可以看出，解析法计算的结果与有限元法计算的结果能够很好地吻合。

表2 三种不同极槽配合的电机Tab.2 Three kinds of PMSM with different pole and slot combinations

图6 解析法和有限元法的电枢反应磁场对比Fig.6 Comparison of armature reaction field calculated by analytical method and FE method

6 谐波分析

图7 为三种电机的电枢反应磁场谐波分析图，由图7a 可知，对于12 对极27 槽电机，电枢反应磁场主要包括次数为N0μ(N0=3,μ=1,2,4,5,7,8,10,…)的谐波成分，由图7b 和图7c 可知，对于14 对极24槽和14 对极36 槽电机，电枢反应磁场主要包括次数为N0μ(N0=2,μ=1,5,7,11,13,…)的谐波成分，这与前面的分析一致。

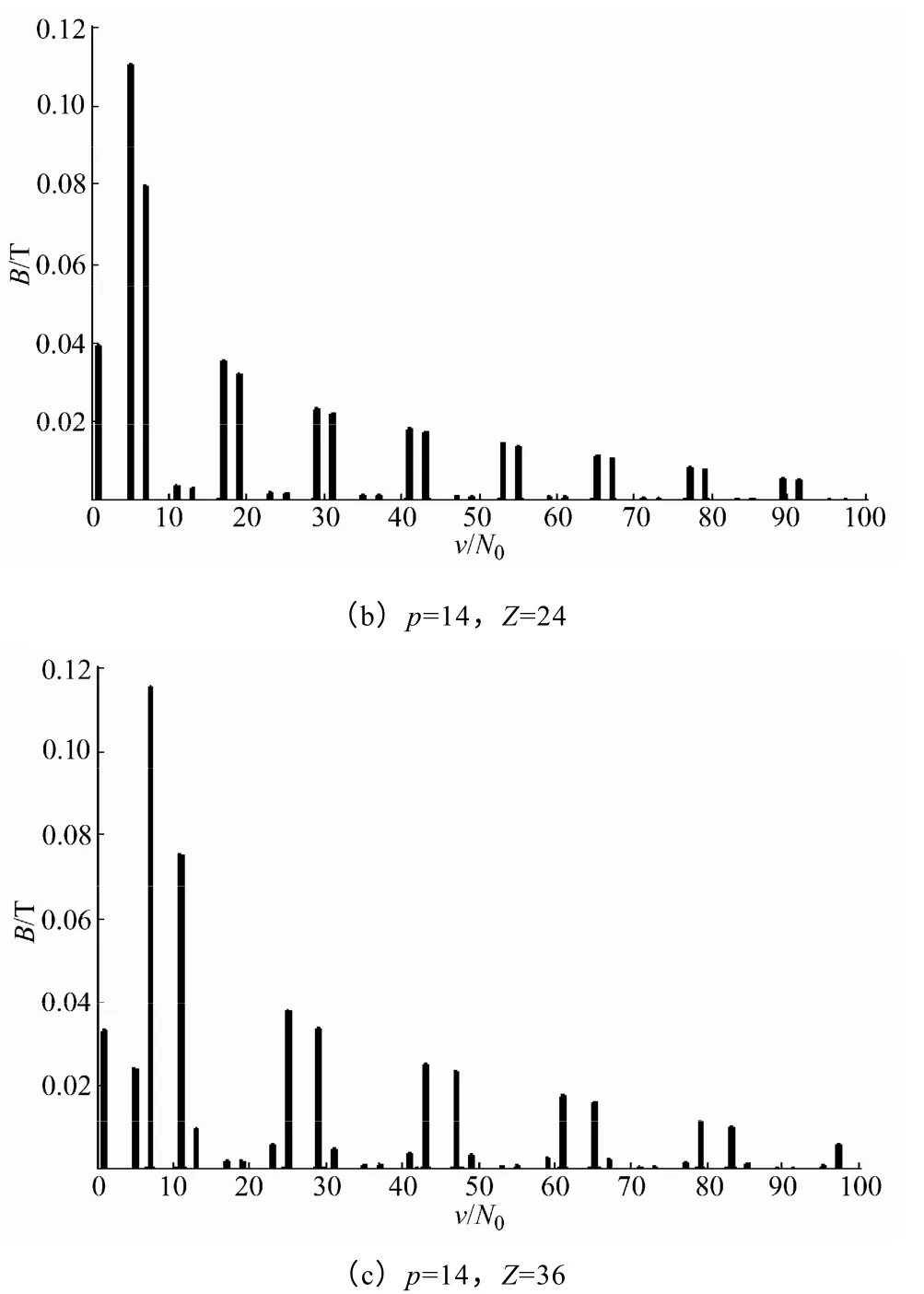
图7 电枢反应磁场的谐波分析Fig.7 Harmonic analysis of armature reaction field

图8 为14 对极24 槽永磁同步电机开槽和不开槽时电枢反应磁场谐波分析对比图，从图中可以看出，开槽并没有引起额外的谐波分量，而主要改变了次数为N0(μ±nZ0)的谐波成分的幅值。

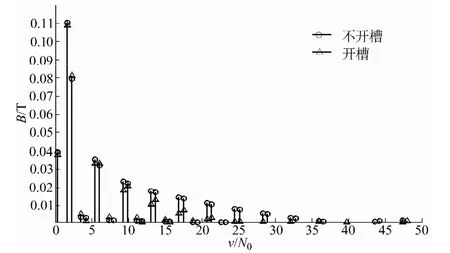
图8 不开槽和开槽时的谐波分析对比Fig.8 Comparison of harmonic analysis without and with slotting effects

7 结论

本文通过不同极槽配合的分数槽集中绕组永磁同步电机绕组排列方式的分析，得到了电枢反应磁场的解析表达式，并通过复数气隙比磁导，考虑开槽对磁场的影响，解析计算的结果与有限元计算的结果的得到了很好的吻合，并且得到如下几个结论：

（1）对于分数槽集中绕组电机，原电机可以认为由N0个单元电机构成，原电机电枢反应磁场所存在的谐波次数是单元电机电枢反应磁场所存在的谐波次数的N0倍。

（2）对于Z0=2p0±1 极槽配合的电机，电枢反应磁场包含次数为 N0μ(μ=1,2,4,5,7,8,10,…)的谐波分量。对于Z0=2p0±2 和Z0=2p0±4 极槽配合的电机，电枢反应磁场包含次数为N0μ(μ=1,5,7,11,13,…)的谐波分量。

（3）定子开槽并不会引入额外的谐波分量，而主要引起次数为 N0(μ±nZ0)的谐波成分的幅值发生变化。

[1]谭建成.三相无刷直流电动机分数槽集中绕组槽极数组合规律研究[J].微电机,2007,40(12):72-77,86.Tan Jiancheng.Investigation on slot/pole number combinations for 3-phase BLDCM with concentrated windings[J].Micromotors,2007,40(12):72-77,86.

[2]陈益广,潘玉玲,贺鑫.永磁同步电机分数槽集中绕组磁动势[J].电工技术学报,2010,25(10):30-36.Chen Yiguang,Pan Yuling,He Xin.Magnetomotive force in permanent magnet synchronous machine with concentrated fractional-slot winding[J].Transactions of China Electrotechnical Society,2010,25(10):30-36.

[3]陈益广.永磁同步电机分数槽集中绕组的槽极数配合及磁动势[C].第十一届全国永磁电机学术交流会,2011:51-60.

[4]田园园,莫会成.分数槽集中绕组永磁交流伺服电机定子磁动势及绕组系数分析[J].微电机,2012,45(4):1-7.Tian Yuanyuan,Mo Huicheng.Stator magneto-motive force and winding coefficient analysis of permanent magnet servo motor with fractional-slot concentrated windings[J].Micromotors,2012,45(4):1-7.

[5]Gaussens B,Hoang E,de la Barriere O,et al.Analytical armature reaction field prediction in field-excited flux-switching machines using an exact relative permeance function[J].IEEE Transactions on Magnetics,2013,49(1):628-641.

[6]Tessarolo A,Mezzarobba M,Degano M.Analytical calculation of air-gap armature reaction field including slotting effects in fractional-slot concentrated-coil SPM multiphase machines[C].2011 International Conference on Power Engineering,Energy and Electrical Drives (POWERENG),2011:1-6.

[7]Wu L J,Zhu Z Q,Staton D,et al.Subdomain model for predicting armature reaction field of surfacemounted permanent-magnet machines accounting for tooth-tips[J].IEEE Transactions on Magnetics,2011,47(4):812-822.

[8]王秀和等.永磁电机[M].北京:中国电力出版社,2011.

[9]Zhu Z Q,Howe D.Instantaneous magnetic field distribution in brushless permanent magnet DC motors,part II:armature-reaction field[J].IEEE Transactions on Magnetics,1993,29(1):136-142.

[10]许实章.交流电机的绕组理论[M].北京:机械工业出版社,1985.

[11]范坚坚,吴建华.计及齿槽极间隔断 Halbach 型磁钢的PMSM 气隙磁场解析分析[J].中国电机工程学报,2010,30(12):98-105.Fan Jianjian,Wu Jianhua.Analytical solution and analysis of airgap magnetic field of PMSM with partition-between-poles halbach magnet considering effect of slotting[J].Proceedings of the CSEE,2010,30(12):98-105.

[12]Zarko D,Ban D,Lipo T A.Analytical calculation of magnetic field distribution in the slotted air gap of a surface permanent-magnet motor using complex relative air-gap permeance[J].IEEE Transactions on Magnetics,2006,42(7):1828-1837.