肿瘤细胞的生长模型与预测治疗

张鹏鸽，朱佑彬，高淑萍

(西安电子科技大学数学与统计学院，西安 710071)

癌症是一大类恶性肿瘤的统称。癌细胞具有无限制、无止境增生的特点，而且肿瘤细胞的生长会大量消耗患者体内的营养物质，同时，还会局部浸入周围正常组织甚至经由体内循环系统或淋巴系统转移到身体其他部分，对人类的生命具有极大威胁。因此，针对这一问题，本文恰当地建立肿瘤细胞增长的数学模型，制定合理的措施以利于及早发现病症并及早治疗，提高存活率，这也是攻克癌症的关键，更是现代医学的重要课题。

首先，我们建立肿瘤细胞的增长模型。在此，先考虑癌症细胞的生长模型，根据模型的生长函数得出肿瘤细胞的倍增次数，再根据倍增次数推出肿瘤细胞的增长函数，并作出图像，求出肿瘤细胞的增长模型;其次，在求解出来模型的基础上，制定出合理的措施，使得病人尽可能早地发现癌症，或者使癌症患者尽可能地延长寿命，此时，则建立优化模型，目标函数是费用少，发现早。

1 资料与方法

由细胞增长的研究可知肿瘤细胞增长的规律特点:①按照现有手段，肿瘤细胞数目超过一定数量时，或肿瘤体积达到一定大小时，临床才能观察到;②在肿瘤生长初期，每经过一定的时间，肿瘤细胞的数目就增加一倍;③在肿瘤生长后期，由于各种生理条件的限制，肿瘤细胞数目逐渐趋向某个稳定值。

基于以上肿瘤细胞的增长特点，利用下面两种模型预测肿瘤数目或体积变化。

1.1 Malthus模型

设肿瘤时刻的体积为V(t)，初始时刻t0的体积为V0，单位时间内肿瘤的增长率为r(r为常数)，并且肿瘤的增长率与当时的体积成正比，则可以得到如下方程:

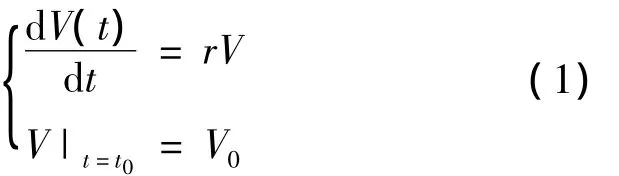
该方程的解为:

在临床应用方面，肿瘤体积增大一倍所需要的时间是刻画肿瘤生长的一个重要参数，记为σ，不难得到:

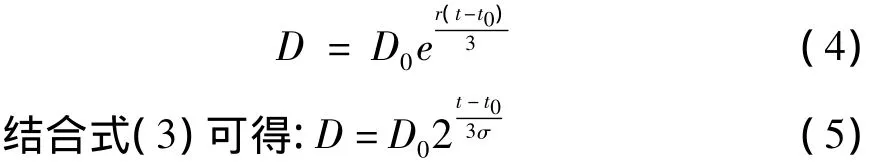
式(4)，(5)即为直径的倍增公式。

令T=t－t0=kσ，k为倍增次数，取对数可得:

转化为体积可得:

根据式(6)，可得一个直径为10μm的癌细胞到临床上能检测出来直径为1 cm的肿瘤细胞时需要分裂约30次，即k约为30。另外根据k的表达式，可以推导出此时的肿瘤细胞数量的函数表达式，假设初始时刻的肿瘤细胞的数量为N0，那么t时刻肿瘤细胞的数量就为:

可以检测出来，细胞倍增30次的时候细胞数量大约是1011，代入式(8)可得N0=93。所以假定初始肿瘤细胞数为93，根据胃癌肿瘤细胞的倍增时间为90 d［6］，结合式(3)可知 r≈0.007 7。

1.2 Logistic模型

在Malthus模型的基础上，我们考虑在肿瘤的增长过程中，由于营养供应有限，将会阻滞肿瘤细胞的增长速度，此时将模型修改为:

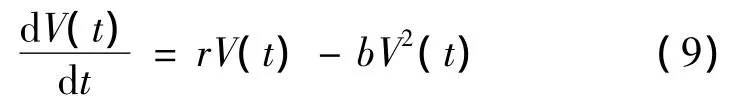
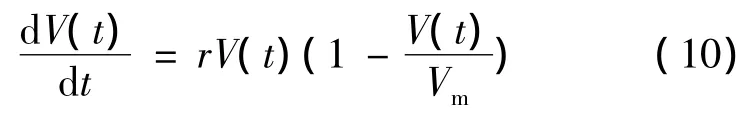
求解可得:

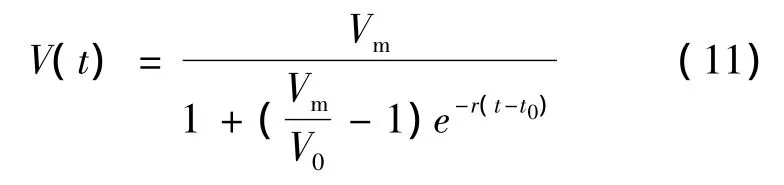
同理可推出:

其中，Dm为肿瘤细胞的最大直径。此时可以得到肿瘤细胞的数量函数表达式是N=N0·2k。

2 结果

根据Malthus和Logistic模型，我们通过MATLAB编程，分别求出Malthus和Logistic模型的肿瘤细胞的生长模型和增长模型结果(见图1－4)。

图1 Malthus模型中直径与时间的关系Figure 1 The diameter-time curve in Malthus model

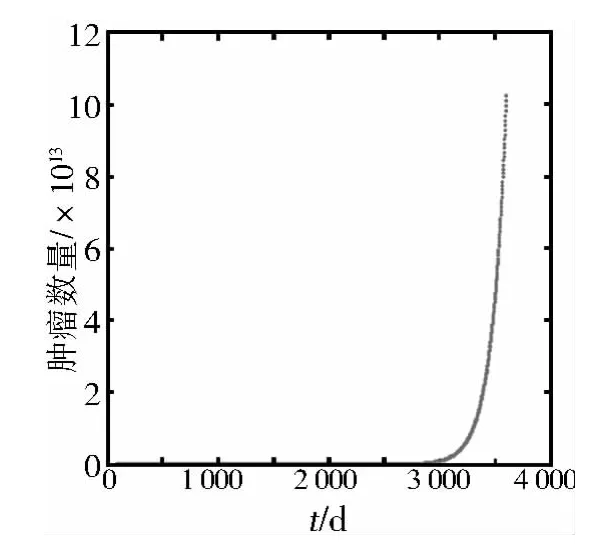
图2 Malthus模型中数量与时间的关系Figure 2 The population-time curve in Malthus model

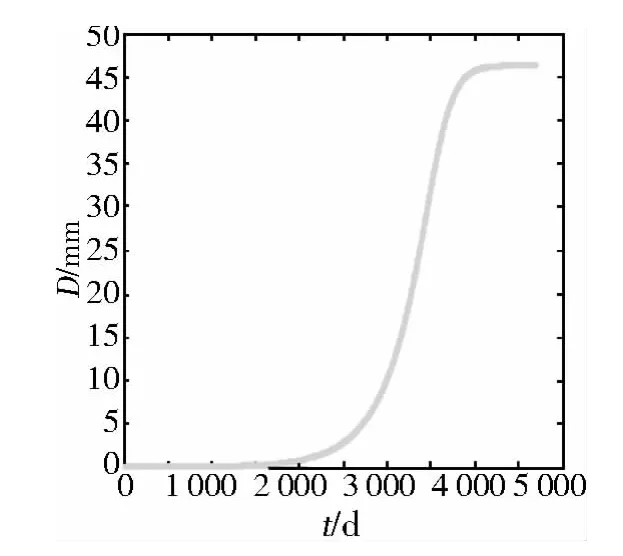
图3 Logistic模型中直径与时间的关系Figure 3 The diameter-time curve in Logistic model

对上面图形进行分析，可以看出Malthus模型比Logistic模型的增长趋势更大，在4 000 d后，Logistic模型趋于稳定，其趋于稳定的最大值 Vm，Nm，即肿瘤体积和数量的最大值，在Malthus模型没有加入限制条件，假定环境无限，肿瘤细胞自由增长，所以曲线一直处于增长状态，在Logistic模型中，加入环境限制，所以肿瘤数量只能趋于一个最大值，不可能无限制增长，直径在1 700 d后就出现明显上升趋势，而数量却在3 000 d后才出现显著增长。从模型得出的数据可以看出在第30次倍增时，肿瘤细胞直径为10.24 mm，数量为1011，此时的结果与实际相吻合，并且发现近期预测时，Malthus模型更适合;在中长期预测中Logistic模型更加合适。

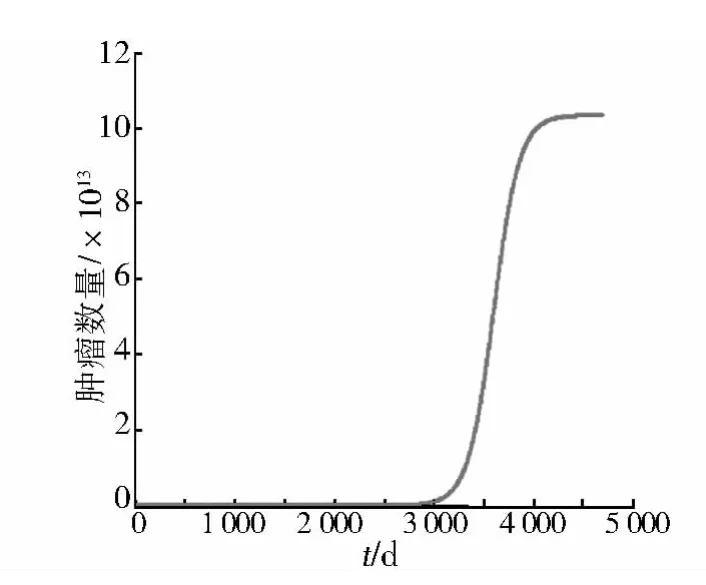
图4 Logistic模型中数量与时间的关系Figure 4 The population-time curve in Logistic model

3 讨论

由于癌症患者只能在倍增30次后才能检测出患有癌症，那就需要制定合理有效的方案使得病人尽早查出癌症并花费最少。

由于肿瘤细胞在倍增到30次后才能被发现，并且在倍增到40次时就一定死亡，针对我们研究的胃癌，假设细胞倍增35次之后就是晚期，那么就需要在倍增35次之前就检测出患有癌症，胃癌的倍增时间是90 d，设每次检查需要p元，要尽量使时间短和费用少，设肿瘤细胞从患者开始检查的时候开始倍增，每次检查间隔时间为d天，截止查出肿瘤细胞一共检查了m次，在肿瘤细胞倍增30次后只要一次检查就可以检查出来是否患有癌症，忽略仪器等的影响，这是双目标问题，则可建立如下模型:

双目标问题不好解决，此时加入权重，考虑到生命比金钱重要，取时间比例和费用分别为和，则模型可以简化为:

若取p=3 000，通过Lingo编程，求解(14)式得出，即需要检查4次，每次检查间隔676d。

这一结果并不理想，只要检查4次，每次检查间隔676 d，接近于2年，这与实际不是很符合，于是，修改假设，将癌症晚期设定为倍增33次，得m=6，d=451，将癌症晚期设定为32次，得m=8，d=338，此时比较符合实际，建议癌症患者每338d检查一次，另外还可以修改权重比例。

综上，本文针对肿瘤细胞的增长建立了Malthus模型和Logistic模型，对肿瘤的直径生长和数量生长进行了建模，得出较为理想的结论。不过模型忽略了很多外界条件，有待于修正。针对检查机制，我们建立了优化模型，将双目标问题改为加权的单目标问题，对模型最后的加权比重和晚期癌症时限进行取值讨论，得出较为理想的结论，这也为临床检查提供了依据。

［1］姜启源，谢金星，叶俊.数学模型［M］.3版.北京:高等教育出版社，2003:135－144.

［2］张学良.Malthus和Logistic模型及其医学应用［J］.数理医药学杂志，2008，21(5):516－518.

［3］Domingues JS.Gompertz model:Resolution and analysis for tumors［J］.JMath Model Appl，2012，1(7):70－77.

［4］Norton L.A Gompertzian model of human breast cancer growth［J］.Cancer Res，1988，48:7067－7071.

［5］Mackenzie D.Mathematical modeling and cancer［J］.SIAM News，2004，37(1):1－3.

［6］Wu CW，Lo SS，Shen KH，etal.Incidence and factors associated with recurrence patterns after intended curative surgery for gastric cancer［J］.World JSurg，2003，27:153－158.