高桩承台桩基波浪受力分析

刘逸敏，姚文娟，张效忠，2，张 峻

（1.上海大学 土木工程系，上海 200072；2.衢州学院 建筑工程学院，浙江 衢州 324000）

跨海大桥作为联系陆路和水上交通的纽带发挥着重要作用，这类海工建筑物多数支撑在桩基结构物上。相比陆上桩基础，水下同类基础面临着更复杂的工作环境。桩基承台组合结构在波浪水流作用下的局部冲刷问题［1－3］、整体受力问题［4］以及波浪、地震下桩基结构的动力响应问题［5］一直是学者们关注的焦点。而在工程设计和施工中，合理确定波浪作用在桩基结构上的作用力和合力作用点通常是设计的控制参数［6］，对工程的造价、安全起着重要作用。高桩承台结构中，圆形承台应用广泛，它是由大尺度圆截面承台和小尺度桩组合而成的复合受力结构。相关研究［7］表明，在一定的入射波浪条件下，由于大尺度结构的存在而产生的波浪绕射对小尺度杆件所受波浪荷载的影响不可忽略。

中国一些学者对东海大桥桥梁桩基承台波浪受力问题进行过一定的研究［8］。基于线性势流理论，Garrett得到了水面处固定截断柱体对波浪散射问题的解析表达，并由姚文伟等［9］推广应用到圆形承台桩基的分析中。Geng等［10］利用高阶边界元法在时域内求解了大尺寸截断圆柱的水波绕射势，结合Morison公式算得了杆件上的波浪受力。通过模型试验，Yuan等［11］研究了规则波下截断圆柱惯性力系数和拽力系数（Cd和Cm）随截断长度的关系。Venugopal等［12－13］实验分析了纯波及波流共同作用时，Cd和Cm的变化规律。利用分离变量法和特征函数展开法，张海燕等［14］、姜胜超等［15］建立了波浪对截断浮式圆柱和淹没圆柱的绕射问题的解析解，并得到了波浪作用在结构上的波浪荷载。采用相同的方法，赖伟［16］、Zheng等［17］推导了水下截断圆柱和无限长矩形结构对水波的绕射和辐射问题及其水动力特性。王均杰等［18］将深水高桩基础的承台部分理想化为浸入水中的截断圆柱体，建立了地震作用下截断圆柱体动水压等效附加质量和等效附加阻尼的计算方法，并提出了矩形截面主体等效为圆柱体的近似计算方法。目前，对于承台浸入水下的高桩承台基础桩柱波浪力研究较少，这影响到了对水下桩基础的全面认识。因此，有必要开展水下承台桩基结构受力的进一步研究。

本文引入浸没承台绕射模型和Morison公式计算了大尺度水下高桩圆形承台的桩柱波浪受力，重点分析了承台相对尺度、淹没水深等因素对桩柱波浪作用力的影响，并在时域内分析了承台下不同位置处桩柱波浪受力的时间序列，旨在为工程设计提供一定的参考。

1 基本原理

1.1 淹没水下承台速度势的求解

基于线性势流理论，参照文献［16］给出的求解方法可得到水下淹没圆柱对入射水波的绕射作用的解析表达。入射条件、结构参数和坐标系统见图1。

图1 水下承台桩柱结构示意图

假定流体是无旋无黏且不可压缩的，则速度势函数在流体域内满足极坐标中的Laplace方程：

式中：Φ为流体速度势；Re［］表示取复函数的实部，φ（r，θ，z）为流体区域内波浪速度势的空间因子，i2＝－1，ω为入射波角频率，t为时间，（r，θ，z）为柱坐标。

将整个流体区域划分为3个区域，分别为外部区域Ω1、承台上部区域Ω2和下部区域Ω3。采用分离变量法，波浪场内3个子空间的绕射速度势ΦD（j）（j＝1，2，3）以及外部区域Ω1内的散射波浪速度势Φs

（1）的形式解［19］可表示为

式中：A为入射波浪波幅，ε0＝1，εm＝2（m≥1），ΦI为入射波速度势。

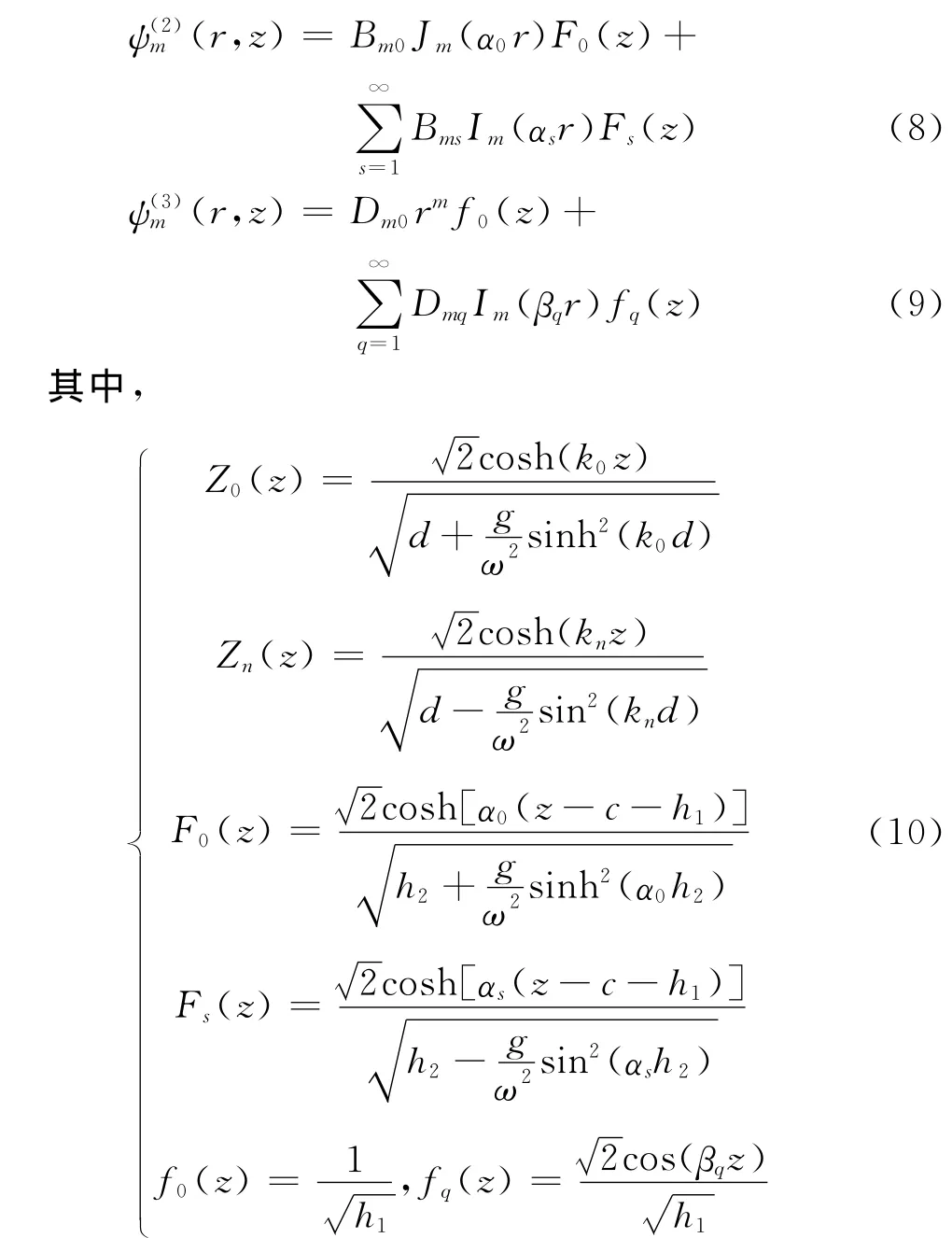
根据边界条件可得式中：Jm（·）为第一类m阶Bessel函数；Hm（1）（·）为第一类m 阶 Hankel函数；Im（·）、Km（·）为修正第一、二类m 阶Bessel函数。k0，km，α0，αs，βq为实数（m，s，q＝1，2…）且满足：

待定系数Amn、Bms、Dmq可通过区域之间连接处的压力和速度连续条件匹配来确定，连接条件的表达为

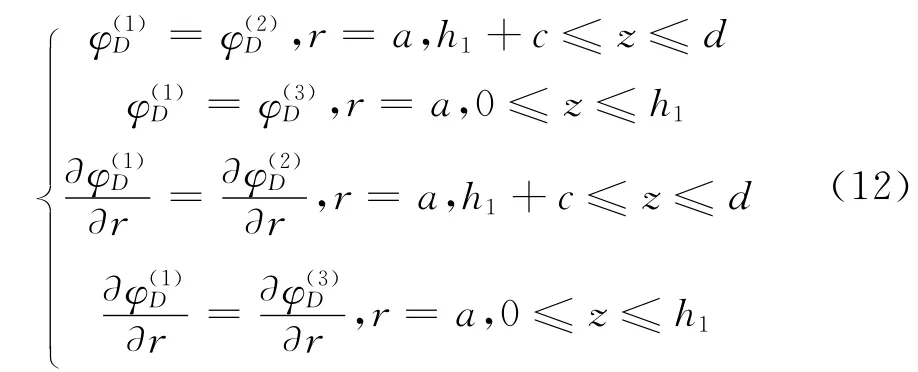
1.2 桩柱波浪力的计算方法

桩柱上的波浪作用力采用线性化的Morison公式计算，该公式是一种半经验半理论的公式，包含惯性力和速度力，即

其中：fi表示惯性力；fd表示速度力；Cm、Cd为质量系数和拖拽力系数，根据《海港水文规范》（JTJ 213－98）的规定各自取为2.0和1.2，ρ为水的密度，D为杆件直径，u、du／dt分别为水质点的速度和加速度。桩柱所在流体区域内由入射波浪产生的速度和加速度的表达式为

2 计算实现及程序编制

根据上述理论用Maple自编了计算程序，流程简图见图2。为了研究不失一般性，考虑典型桩基布置方式如图3，桩柱均为直立桩形式，θD为桩心角（即桩柱中心连线与x轴正向的夹角），rD为桩心距（即边桩距结构几何中心的距离），对不同位置桩体受力进行了分析。

图2 程序流程图

图3 桩基布置

3 计算结果分析与讨论

3.1 理论计算模型的验证

为了验证所提计算方法及程序编译的正确性，通过与流体计算流体软件Fluent模拟结果进行对比验证。基于动量源造波原理，在Fluent中使用UDF自定义函数模拟了承台桩基模型在给定入射条件下中心处直桩受力，计算参数为：水深d＝10m，承台厚度c＝3m，承台半径a＝3m，浸没深度h2＝1m，波长L＝20m，波幅A＝1m，入射波频率ω＝1.752s。图4为数值波浪水槽示意图，工作区域内截取的桩基承台模型见图5，图6为t＝12s时的波面分布。从图7给出了解析值与数值模拟值的对比，从计算结果可以看出，两者吻合较好。上述所提方法和编写的程序是准确可靠的。

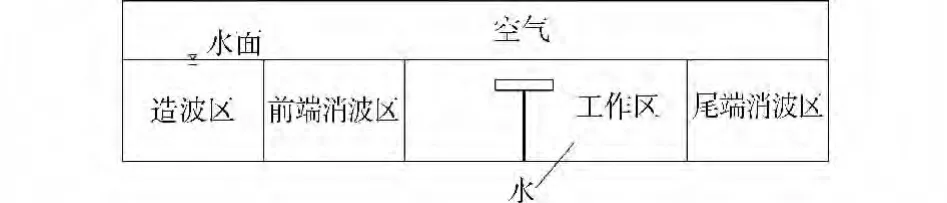
图4 波浪水槽示意图

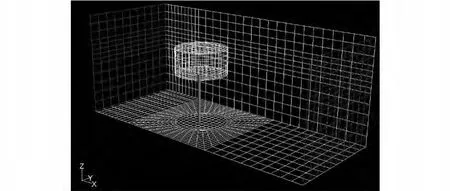
图5 高桩承台数值模型图

图6 波面高度分布（t＝12s）

3.2 中心桩波浪受力分析

为了便于分析承台的存在对单桩受力变化的影响，这里先定义几个承台效应系数Kf、Km和Ke，即

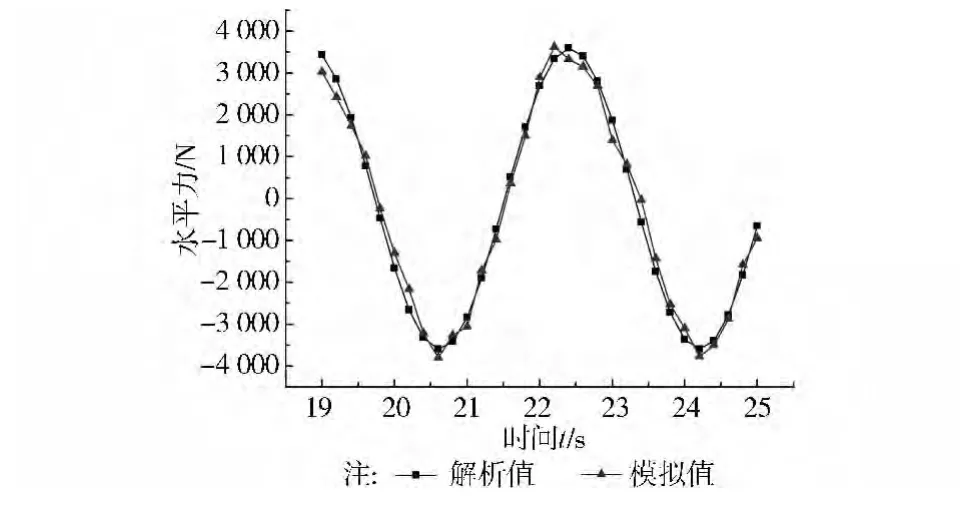
图7 数值模拟与解析方法的对比

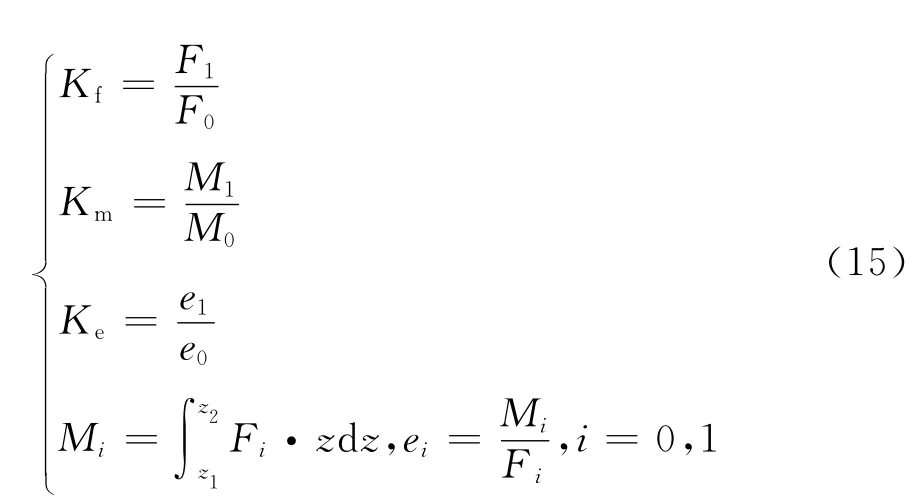
其中：下标1表示考虑承台效应时中心桩柱受到波浪作用力；下标0表示一般情形下的单桩柱受力；Fi为水平总波力；Mi为水平总波力距；ei为合力作用点。

考虑水深d＝20m，入射波浪波长L＝40m，波幅A＝1m的规则波入射时，两种不同尺寸的承台在不同浸入深度h2时，Kf、Km和Ke的计算结果见表1。

表1 承台效应系数随淹没深度的变化

从表1看出，在给定入射条件下，随淹没深度的增加承台效应越来越明显；其中，Km，Ke随着h2／d的增大而减小，而Kf因承台尺寸的改变将有不同的变化规律，即当承台尺寸较大时，Kf将随h2／d的增大而增大，承台尺寸较小时，Kf的变化规律正好相反。

考虑2种承台的尺寸为a／d＝0.3，c／d＝0.10和a／d＝0.4，c／d＝0.15，相对浸入深度h2／d＝0.10，图8（a）～（c）给出了 Kf、Km、Ke随无量纲入射波数ka的变化规律。计算结果表明，Kf、Km随着波数ka的增加而减小且两者变化趋势相同，区别在于Km的改变略缓于Kf，Ke随着波数ka的增加而先增大后减小；当承台尺寸较大时，将明显的减小桩柱上的波力和波力矩，起到很好的“遮蔽保护”作用，Ke的变化曲线的拐点将在特定的波浪尺度时出现。

图8 承台效应系数随无量纲波数ka的变化规律

3.3 边桩波浪受力分析

上一节讨论的中心桩只是rd＝0的特例，对于工程中普遍采用的群桩结构，布置在不同位置的边桩柱由于其桩心角θD和桩心距rD的不同，往往使得群桩中各组成桩的波浪受力与单桩有较大差别。

这里取c＝3m，a＝7m，d＝20m，入射波波幅A＝1m，波浪周期T＝5.07s，rD／a＝4／7，桩柱直径D＝1m。图9给出了桩基承台结构中直桩波浪力幅值与桩心角θD的关系，其中Fmax、Fmax0分别为考虑承台时及无承台时相同波浪要素下的桩柱波浪力幅值。结果表明，承台下部桩柱上的波浪力幅值在中心距固定的情形下，当相对浸入深度h2／d＝0.15、0.20、0.25时，桩柱波浪力幅值随着桩心角的变大而先增加后减小并在θD＝π／3～π／2附近达到最大值；当相对浸入深度h2／d＝0.05、0.10时，桩柱波浪力幅值随着桩心角的变大而减小；几种情形下，波浪力幅值都在θD＝π时达到最小值，且关于θD＝π对称。由计算结果可以知道，一般情况下群桩系数可以取在0.70～0.75之间。

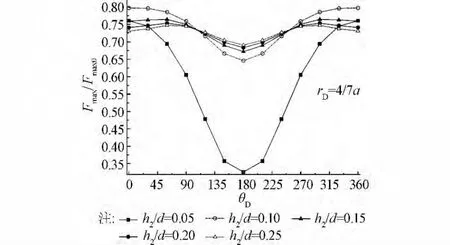
图9 直桩柱波浪力幅值与桩心角θD的关系

图10（a）～（g）给出了不同位置处桩柱波浪受力的时间变化过程曲线，横坐标为无量纲的时间序列t／T，纵坐标为无量纲的波浪力幅值Fx／F0，Fy／F0，其中，Fx、Fy与F0分别表示考虑承台时桩柱x方向和y方向的波浪力与不考虑承台时相同位置的桩柱受力。从图中我们可以看出，沿波浪传播方向的力Fx都小于不考虑承台时的波向力，垂直于波浪传播方向的力Fy最多大约能占达到波向力Fx的40%左右；迎浪侧波向力Fx小于背浪侧Fx，而迎浪侧Fy大于背浪侧Fy；Fx与Fy之间的相位差最大约为T／4。在波向线过结构中心之外的桩柱，将受承台存在的影响而引起波向力的偏转，如果对桩柱进行动力分析时应额外考虑这个因素的贡献。

4 结论

通过引入浸没承台绕射模型和Morison公式计算了水下高桩承台的桩基波浪受力，并将其与数值模拟的结果进行了对比，验证表明该方法是可行的。得到的主要结论如下：

1）承台效应对桩柱的影响将随淹没深度的增加越来越明显，不同的承台与波浪比尺将产生相反的变化规律；承台效应系数随入射波数的增加而减小，合力作用点将在波数ka＝0.8～1.2之间出现拐点；承台的存在将对桩柱受力起到很好的“遮蔽保护”作用。

2）当承台淹没深度较浅时，桩柱波浪力幅值随着桩心角的变大而先增加后减小并在θD＝π／3～π／2附近达到最大值，淹没深度较深时桩柱波浪力幅值随着桩心角的变大而减小；波浪力幅值都在θD＝π时达到最小值，群桩系数一般情况下可取为0.70，留有余地情况下可取0.75。

图10 rD／a＝4／7时不同中心角桩柱受力时间序列

3）迎浪侧波向力Fx小于背浪侧Fx，而迎浪侧Fy大于背浪侧Fy；Fx与Fy之间的相位差大约为T／4，承台的存在将引起波向力的偏转。

［1］Ataia－Ashtiani B，Baratian－Ghorghi Z，Beheshti A A.Experimental investigation of clear－water local scour of compound piers［J］.Journal of Hydraulic Engineering，2010，136（6）：343－351.

［2］Amini A，Melville B W，Ali T M，et al.Clear－water local scour around pile groups in shallow－water flow［J］.Journal of Hydraulic Engineering，2012，138（2）：177－185.

［3］Liang D F，Gotoh H，Scott N，et al.Experimental study of local scour around twin piles in oscillatory flows［J］.Journal of Waterway，Port，Coastal and Qcean Engineering，2013，139（5）：404－412.

［4］Guo C S，Zhang N C，Pei Y G.Numerical study of wave loads on a caisson－pile－deck composite structure over permeability seabed ［J］.Journal of Shanghai Jiaotong University：Science，2012，17（1）：82－90.

［5］武崇福，刘贝贝.波浪和地震作用下高桩承台－土－结构动力响应［J］.土木建筑与环境工程，2011，33（6）：7－12.Wu C F，Liu B B.Dynamic response analysis of highrise pile cap－soil－structure under the wave and earthquake action［J］.Journal of Civil，Architectural ＆Environmental Engineering，2011，33（6）：7－12.

［6］徐伯勤.对作用桩基上的波流力计算中若干值得注意的问题的探讨［J］.水运工程，2008（10）：41－45.Xu B Q.Matters of attention in computation of wave current force applied on pile foundation［J］.Journal of Port ＆ Waterway Engineering，2008（10）：41－45.

［7］耿宝磊，腾斌，宁德志，等.畸形波作用下海洋平台小尺度杆件波浪荷载分析［J］.大连海事大学学报，2010，36（1）：39－43.Geng B L，Teng B，Ning D Z，et al.A time－domain analysis of wave force on small－scale cylinders of platform under freak waves ［J］.Journal of Dalian Maritime University，2010，36（1）：39－43.

［8］Liu S X，Li Y C，Li G W.Wave current forces on the pile group of base Foundation for the East Sea Bridge，China［J］.Journal of Hydrodynamics，2007，19（6）：661－670.

［9］姚文伟，刘桦.规则波中圆形承台对桩基波浪力的影响［J］.力学季刊，2009，30（3）：357－362.Yao W W，Liu H.Effect of circular slab fo wave loads on piles in regular waves ［J］.Journal of Chinese Quarterly of Mechanics，2009，30（3）：357－362.

［10］Geng B L，Teng B，Ning D Z.A time－domain analysis of wave force on small－scale cylinders of offshore structures ［J］.Journal of Marine Science and Technology，2010，18（6）：875－882.

［11］Yuan Z D，Huang Z H.An experimental study of inertia and drag coefficients for a truncated circular cylinder in regular waves ［J］. Journal of Hydrodynamics，2010，22（Sup1）：318－323.

［12］Venugopal V，Varyani K S，Barltrop N D P.Wave force coefficients for horizontally submerged rectangular cylinders［J］.Ocean Engineering，2006，33：1669－1704.

［13］Venugopal V，Varyani K S，Westlake P C.Drag and inertia coefficients for horizontally submerged rectangular cylinders in waves and currents［J］.Journal of Engineering for the Maritime Environment，2009，223（1）：121－136.

［14］张海燕，赵文斌，唐友刚.深水Spar平台主体波浪载荷计算［J］.中国海洋大学学报：自然科学版，2008，38（3）：508－512.Zhang H Y，Zhao W B，Tang Y G.Calculation of wave loads acting on a Spar hull in deep water［J］.Periodical of Ocean University of China：Natural Science Edition，2008，38（3）：508－512.

［15］姜胜超，腾斌，宁德志，等.波浪对淹没垂直圆柱绕射解析解［J］.海洋工程，2010，28（3）：68－75.Jiang S C，Teng B，Ning D Z，et al.An analytical solution of wave diffraction by a submerged vertical cylinder［J］.Journal of the Ocean Engineering，2010，28（3）：68－75.

［16］赖伟.地震和波浪作用下深水桥梁的动力响应研究［D］.上海：同济大学，2004.

［17］Zheng Y H，Liu P F，Shen Y M，et al.On the radiation and diffraction of linear water waves by an infinitely long rectangular structure submerged in oblique seas［J］.Ocean Engineering，2007，34：436－450.

［18］王君杰，赖伟，胡世德.深水高桩基础桥梁地震水动力效应分析［J］.同济大学学报：自然科学版，2011，39（5）：650－655.Wang J J，Lai W，Hu S D.Seismic hydrodynamics effects on group－pile foundations with caps merged in water ［J］.Journal of Tongji University：Natural Science，2011，39（5）：650－655.

［19］李玉成，滕斌.波浪对海上建筑物的作用［M］.2版.北京：海洋出版社，2002：50－60.