柱下端局部采用FRC材料钢筋混凝土柱的承载力分析

徐 洁，梁兴文，王 海，康 力

（1.西安建筑科技大学 土木工程学院，西安 710055；2.陕西工业职业技术学院 土木工程学院，陕西 咸阳 712000；3.中石油华东勘查设计研究院，山东 青岛 266071）

为了改善钢筋混凝土柱的抗震性能，学者们进行了大量的试验研究和理论分析，提出了一些较为有效的措施，如对柱端的箍筋进行加密、改善箍筋形式等［1－5］。 中国规范［6－7］也对柱端箍筋加密区的长度、箍筋间距和直径给出了明确的规定。但震害表明，在强震作用下，柱端箍筋加密区附近保护层混凝土严重剥落，影响震后恢复重建。文献［8］的研究结果表明：当配箍率增大到一定程度后，柱的地震位移反应趋于稳定，柱的屈服荷载和初始水平刚度受配箍率影响不大。因此，需寻求其他措施以改进钢筋者［9－13］及本课题组［14－15］前期的研究结果表明：FRC有超高的受拉应变硬化性能，可用于以受剪为主的构件和高剪应力作用下的受弯构件；有很大的受压应变能力，可减少或取消抗震构件的约束钢筋数量；FRC增大了受弯和受剪构件的受剪强度、变形能力和损伤容限，即使在无横向钢筋或横向钢筋很少的情况下，构件仍具有很高的受剪强度、变形能力和损伤容限。特别是FRC已走上了绿色化的道路，经纤维与活性掺合料有效复合，不仅节约了大量的资源和能源，保护了生态环境，而且经过界面结构的优化和强化、界面效应和界面粘结的发挥与提高，又进一步强化了混凝土材料各项关键性能，大幅度地提升了结构的耐久性，延长了材料和结构的服役寿命。

为了充分发挥FRC的上述优点，将FRC用于钢筋混凝土柱潜在的塑性铰区，柱的其余部分仍采用普通混凝土，以便改善钢筋混凝土柱的抗震性能和抗剪性能，从而减轻地震引发的结构破坏。通过对5根塑性铰区采用FRC柱以及1根钢筋混凝土柱的拟静力对比试验，研究其破坏机理，并建立其承载力计算方法。混凝土柱的抗震性能。

纤维增强混凝土（Fiber Reinforced Concrete，简称FRC）是一种高韧性的混凝土。一些研究

1 试验概况

1.1 试件设计

设计制作了5根FRC柱及1根钢筋混凝土柱，以混凝土强度等级、轴压比和FRC区高度为变化参数。原型柱为净高3m、截面边长为500mm的正方形框架柱，缩尺比例为1∶2.5。模型柱边长均为200mm×200mm，剪跨比均取3.0，各柱的纵向钢筋均为412，箍筋按非抗震构造要求配置（从底梁顶面起算，200mm以内，为（φ6＠100；200mm 以上为（φ6＠150），详见图1。

试件编号、基体强度等级、FRC区高度、FRC的水胶比、实际轴压比、设计轴压比以及各试件所加轴向力见表1。各试件的尺寸及配筋详图见图1。

1.2 材性试验

试验所用普通混凝土和FRC的配合比及相应的立方体抗压强度平均值见表2。纵向受力钢筋采用HRB400级热轧带肋钢筋，箍筋采用HPB235级热轧光圆钢筋，其力学性能指标见表3，其中fy、fu分别表示钢筋屈服强度、极限强度的试验平均值。

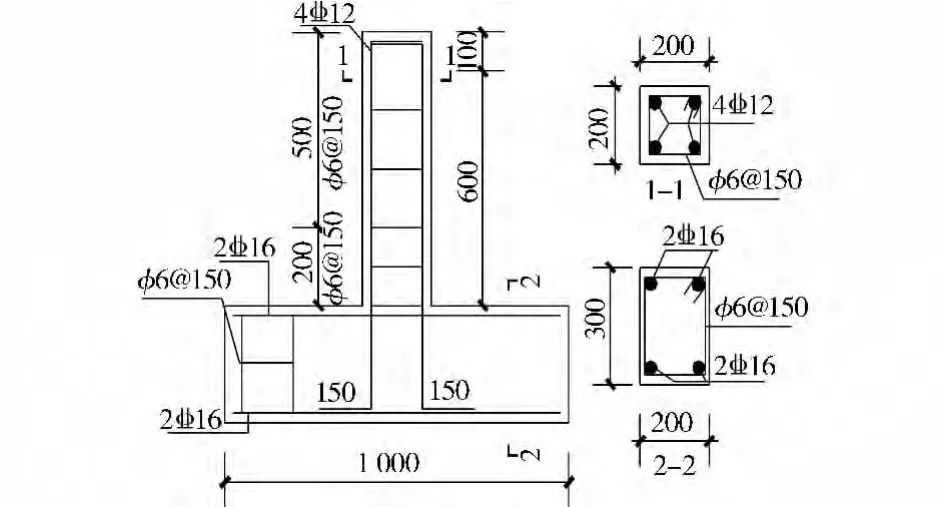
图1 试件尺寸及配筋图

表1 试件基本参数

表2 混凝土的配合比及其强度

表3 钢筋的力学性能

1.3 试验装置和加载制度

试验时，首先用竖向油压千斤顶施加轴向荷载并在试验过程中保持不变，然后施加反复水平荷载。水平荷载采用荷载－位移混合控制方法，试件屈服前按荷载控制，正、反向加载、卸载各1次，直至试件屈服。随后进入位移控制循环，控制位移取为屈服位移的倍数，每一控制位移下循环3次，直至水平荷载显著降低（小于峰值荷载的85%）或试件不能稳定地承受轴向荷载时，停止试验。试件加载简图如图2所示，加载装置如图3所示。

图2 试验简图

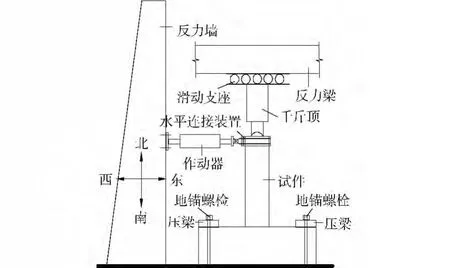
图3 加载装置简图

2 试验结果分析

在纵向受力钢筋屈服前，塑性铰区出现少量细微水平裂缝和斜裂缝，其加载与卸载曲线基本重合为一条直线，试件基本处于弹性受力阶段。卸载时可观测到裂缝闭合现象，卸载后残余变形很小。在水平荷载达到屈服荷载（70～80kN）时，荷载－位移滞回曲线出现拐点，受力钢筋屈服，6个试件柱顶侧移角平均值为1／64。此后改为按屈服位移Δy的整倍数控制加载循环。随着水平位移的增加，柱脚原有水平裂缝的宽度增大，形成一条裂缝宽度相对较大的水平裂缝；随着水平位移的逐渐增加，荷载略有上升，达到峰值荷载（86～110kN）时，FRC柱的顶点侧移角平均值为1／19.7，钢筋混凝土柱（试件RC6）的柱顶侧移角为1／30，各试件的裂缝分布情况如图4所示。

当水平位移达到2倍的屈服位移时，试件RC6的主要斜裂缝不断延伸、扩展，柱脚部位保护层混凝土不断被压碎、脱落，主筋及箍筋外露，构件承载力下降，表现为突然的剪切破坏。当达到极限承载力时，试件FRC1～FRC5破坏以腹剪斜裂缝向两端发展，逐渐贯通、变宽，形成临界斜裂缝，同时受压区混凝土向三个面外鼓，以压坏为特征达到破坏。破坏时，5个FRC柱的顶点侧移角平均值为1／15.7（其中试件 FRC5为1／13.6），钢筋混凝土柱（试件RC6）的顶点侧移角为1／30，各试件的最终破坏形态如图5所示。

图4 峰值荷载时的裂缝分布

图5 试件的破坏形态

由于6个试件的箍筋配置均较少，所以均表现为纵向钢筋屈服后的剪切破坏。钢筋混凝土柱（试件RC6）在达到峰值荷载后突然破坏，斜裂缝较徒，具有明显的脆性。试件FRC1～FRC5下端局部使用FRC，由于裂缝界面上纤维的桥联作用，混凝土抗剪能力增强，推迟了剪切破坏的发生。破坏时，临界斜裂缝由细密的平行斜裂缝逐渐贯通形成，出现的位置也被控制在FRC区域，避免RC区发生突然的脆性破坏，最终产生具有一定延性特征的弯剪型破坏。

另外，现行抗震规范［6］规定，钢筋混凝土框架结构的弹塑性层间侧移角限值为1／50，与其相应的层间侧移角实际值约为1／30～1／20。由上述破坏过程可见，在FRC柱达到峰值荷载时，其相应的侧移角平均值为1／19.7，且相应的破坏程度（图4）较轻，稍加修复即可继续使用。这表明，FRC柱比RC柱具有更好的变形能力和损伤容限。

3 压弯承载力分析

3.1 基本假定

对FRC柱进行压弯承载力分析时，采用下列假定：

1）FRC材料在单轴受拉时存在应变硬化现象（图6（a）），为简化计算，假定其应力 应变曲线为双直线形式［16］（图6（a）），则单轴受拉应力应变关系为

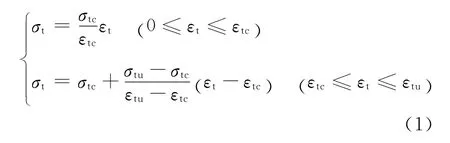
单轴受压情况下，应力 应变曲线的上升段采用二次抛物线［16］，下降段采用水平直线，如图6（b）所示，应力应变关系为

式中：σtc为FRC受拉初裂强度；εtc为FRC受拉初裂应变；σtu为FRC极限抗拉强度；εtu为FRC极限拉应变；ε0为FRC峰值压应变；σcu为FRC极限抗压强度；εcu为FRC极限压应变。

式中：fy、εy、Es分别为钢筋的屈服强度、屈服应变和弹性模量；εs，h为钢筋强化起点应变。

3）FRC柱受力变形后，截面各点应变符合平截面假定。

4）柱截面受拉区，在拉应变小于εtu的区域，考虑截面上FRC的受拉作用。

3.2 柱截面受弯承载力及相应的水平剪力

3.2.1 不考虑柱截面受拉区FRC的作用 在柱达到承载能力极限状态时，裂缝截面受拉区混凝土退出工作，截面受拉区的拉力主要由受拉钢筋承受。对于试验中受拉钢筋首先屈服的对称配筋矩形截面压弯柱，其截面受弯承载力可按式（4）计算［17］。

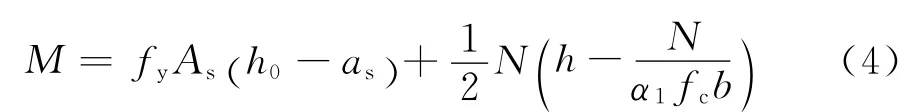
式中符号意义同文献［17］。

相应的柱水平承载力为

式中，a表示柱加载点至固定端的距离，试验柱取a＝600mm。

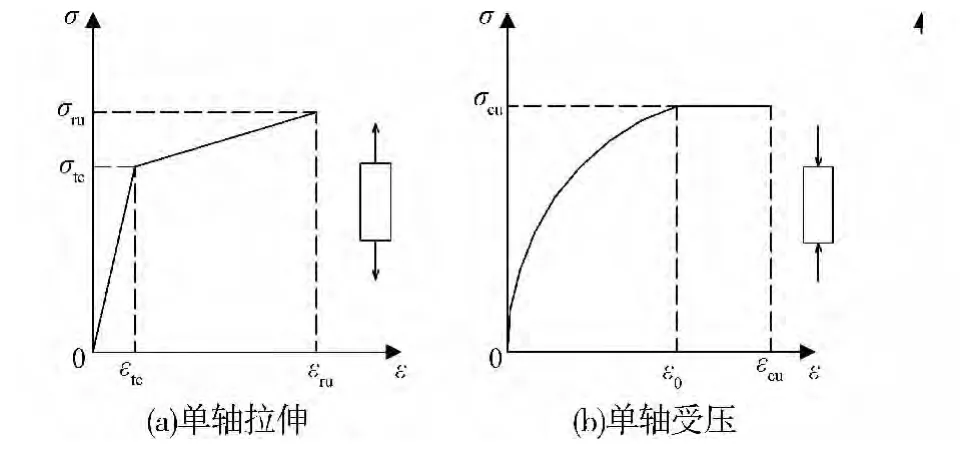
图6 FRC的应力应变曲线

3.2.2 考虑柱截面受拉区FRC的作用 考虑FRC材料在单轴受拉状态时的应变硬化特点，在截面受拉区，在拉应变小于εtu的区域，可考虑截面上FRC的受拉作用。根据假定3）和4），可得图7所示的截面应变和应力图。

为简化计算，受拉区FRC应力分布图形等效为梯形和三角形。受拉区三角形应力分布高度为xtc；受拉区梯形应力分布高度为xtu；受拉区梯形形心至梯形长底边距离为t；拉应变大于εtu的截面高度为xt；FRC受压区高度为x；受压区合力至中和轴距离为y。

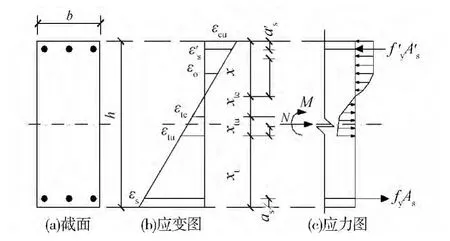
图7 柱控制截面的计算简图

对于受拉钢筋首先屈服的对称配筋矩形截面压弯柱，由力的平衡条件可得

式中

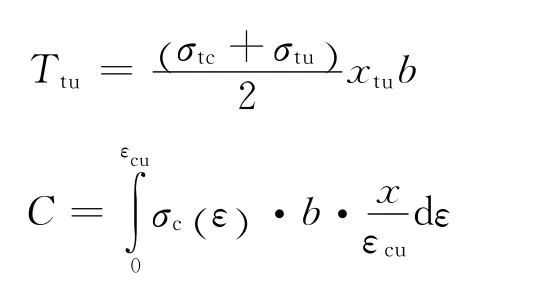
由截面应变图可得

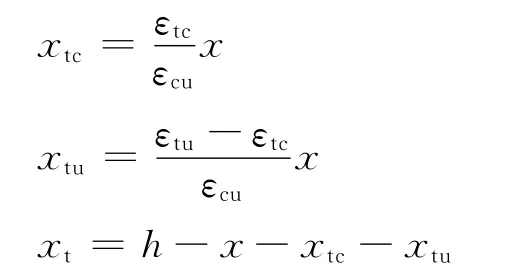
将上述各式代入（6）式可求得x。

受压区合力至中和轴距离为

梯形形心坐标由组合图形求形心坐标公式得。

对受拉钢筋合力点取矩，得截面的受弯承载力

相应的柱水平承载力仍按式（5）计算。

分别按式（4）和式（7）计算弯矩，并按式（5）计算柱的水平承载力，其计算值与试验值及其比较结果见表4。

表4 按正截面破坏所得试件水平承载力计算值与试验值比较

由表4可见：1）考虑与不考虑FRC作用所得的水平承载力相差在10%左右，故设计时可考虑截面受拉区FRC的作用；2）如假定柱为压弯破坏，则所得水平承载力计算值与试验值相差较多，表明柱是弯曲屈服后的剪切破坏。

4 受剪承载力分析

由前述试验结果可知，试验的6根柱均为弯曲屈服后的剪切破坏，故应分析其受剪承载力。对于承受水平荷载和轴向荷载的钢筋混凝土柱，其斜截面受剪承载力主要由两部分组成：混凝土所负担的剪力和箍筋所负担的剪力。箍筋所负担的剪力，可采用桁架模型计算［7］，即

式中符号意义同文献［7］。

假定柱弯剪区段内的混凝土在压、弯、剪共同作用下，其主拉应力达到混凝土抗拉强度时，该区段发生剪切破坏。由材料力学可得

对于图2所示柱，如设定水平轴为x轴，竖轴为y轴，则式（10）中的σx＝0，σy＝－N／A，其中N 为轴向压力；A为柱的横截面面积。将σx＝0、σy＝－N／A以及σ1＝ft代入式（10），可得

则混凝土所负担的剪力Vc为

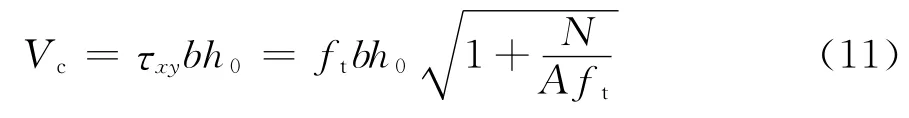
由于随剪跨比增加，混凝土的受剪承载力将降低，故考虑剪跨比λ后，式（11）变为

式中：n为轴压比，n＝N／（fcA）。

综上所述，钢筋混凝土柱的受剪承载力可表示为

按式（13）计算6个柱试件的受剪承载力，并与试验值进行比较，结果见表5。可见，柱受剪承载力的计算值与试验值比较吻合，表明6根柱均是弯曲屈服后的剪切破坏，与试验现象比较符合。

表5 最大荷载的剪力计算值与试验值对比

另外，由表5可见，5个下端局部使用FRC的柱，其水平承载力试验值均高于钢筋混凝土柱，表明FRC材料能提高柱的水平承载力，相应地也提高了峰值荷载对应的水平位移。这是由于FRC材料具有良好的抗剪性能，所以提高了其受剪承载力。

5 结论

1）试验结果表明，下端局部使用FRC、且配置较少箍筋的钢筋混凝土柱，其临界斜裂缝由细密的平行斜裂缝逐渐贯通形成，避免了FRC区发生突然的脆性破坏，表现为在试件达到峰值荷载后，承载力缓慢下降，最终产生具有一定延性特征的弯剪型破坏。

2）计算结果表明，对于承受水平和竖向荷载、局部使用FRC的柱，计算其压弯承载力时可考虑控制截面受拉区FRC材料的受拉作用，其对柱承载力计算值的影响在10%左右。

3）试验及计算结果均表明，下端局部采用FRC且箍筋配置较少的钢筋混凝土柱为弯曲屈服后的剪切破坏。FRC材料能延缓柱发生剪切破坏，具有较好的抗剪性能。

4）建立的局部使用FRC柱受剪承载力计算公式（13），是试验结果的平均值，仅用于对试验结果进行分析。

［1］Bechtoula H，Mehani Y，Kibboua A，et al.Seismic behavior of high strength reinforced concrete columns under reversed cyclic loading ［C］／／15th World Conference on Earthquake Engineering，2012：24－28.

［2］吕西林，郭子雄，王亚勇.RC框架梁柱组合件抗震性能试验研究［J］.建筑结构学报，2001，22（1）：1－7.Lu X L，Guo Z X，Wang Y Y.Experimental study on seismic behavior of beam－column subassemblages in RC frame［J］.Journal of Building Structures，2001，22（1）：2－7.

［3］王全风，沈章春，杨新勇，等.HRB400级钢筋混凝土短柱抗震性能试验研究［J］.建筑结构学报，2008，29（2）：114－117.Wang Q F，Shen Z C，Yang Y X，et al.Seismic behavior of HRB400reinforcement concrete columns［J］.Journal of Building Structures，2008，29（2）：114－117.

［4］Essawy A，elHawary M.Strength and ductility of spirally reinforced rectangular concrete columns ［J］.Construction and Building Materials，1998，12（1）：31－37.

［5］Li B，Park R.Confining reinforcement for high－strength concrete columns［J］.ACI Structural Journal，2004，101（3）：314－324.

［6］GB 50011—2010建筑抗震设计规范［S］.北京：中国建筑工业出版社，2010.

［7］GB 50010—2010混凝土结构设计规范［S］.北京：中国建筑工业出版社，2010.

［8］张勤，贡金鑫，姜凤娇，等.钢筋混凝土柱非线性特性的分析方法［J］.土木建筑与环境工程，2011，33（6）：51－58.Zhang Q，Gong J X，Jiang F J，et al.Analysis method for nonlinear properties of reinforced concrete columns［J］.Journal of Civil，Architectural and Environmental Engineering，2011，33（6）：51－58.

［9］姜睿，徐世烺，贾金青.高轴压比PVA纤维超高强混凝土短柱延性的试验研究［J］.土木工程学报，2007，40（8）：54－60.Jiang R，Xu S L，Jia J Q.An experimental study on the seismic ductility of PVA fiber supper－high－strength concrete columns with high axial load ratios［J］.China Civil Engineering Journal，2007，40（8）：54－60.

［10］张君，居贤春，郭自力.PVA纤维直径对水泥基复合材料抗拉性能的影响［J］.建筑材料学报，2009，12（6）：706－710.Zhang J，Ju X C，Guo Z L.Tensile properties of fiber reinforced cement composite with different PVA fibers［J］.Journal of Building Materials，2009，12（6）：706－710.

［11］王晓刚，Wittmann F H，赵铁军.优化设计水泥基复合材料应变硬化性能研究［J］.混凝土与水泥制品，2006，149（3）：46－49.Wang X G，Wittmann F H，Zhao T J.Optimize the design of engineered cementitious composites strain hardening properties ［J］.China Concrete and Cement Products，2006，149（3）：46－49.

［12］Gustavo J，Parra M.High－performance fiber－reinforced cement composites：An alternative for seismic design of structures［J］.ACI Structural Journal，2005，102（5）：668－675.

［13］Fischer G，Li V C.Deformation behavior of fiberreinforced polymer reinforced engineered cementitious composite （ECC）flexural members under reversed cyclic loading conditions［J］.ACI Structural Journal，2003，100（1）：25－35.

［14］李艳，梁兴文，刘泽军.高性能生态建筑材料PVA－ECC的试验研究［J］.工业建筑，2011，41（4）：97－102.Li Y，Liang X W，Liu Z J.Experimental research on preparation of ecological cementitious composites PVAECC［J］.Industrial Construction，2011，41（4）：97－102.

［15］Li Y，Liang X W，Liu Z J.Behavior of high performance PVA fiber reinforced cement coomposites in triaxial compression ［J］. Journal of Wuhan University of Technology，2010，32（17）：179－185.

［16］Chung C H.Computational and hybrid simulation of high performance fiber reinforced concrete coupled wall systems［D］.America：Univisity of Michigan，2010.

［17］梁兴文，史庆轩.混凝土结构设计原理［M］.北京：中国建筑工业出版社，2011：151－152.