语音识别中基于低秩约束的本征音子说话人自适应方法

张文林张连海 陈 琦 李弼程

(解放军信息工程大学信息系统工程学院 郑州 450002)

1 引言

在现代连续语音识别系统中，说话人自适应是一个必不可少的关键模块。对于传统的基于隐马尔可夫模型(Hidden Markov Model, HMM)-高斯混合模型(Gaussian Mixture Model, GMM)的语音识别系统，说话人自适应技术就是在给定少量说话人相关语料的条件下，根据最大似然(Maximum Likelihood, ML)或最大后验(Maximum A Posteriori, MAP)准则，对说话人无关(Speaker Independent, SI)系统中每一个GMM的高斯均值矢量进行调整，得到说话人相关(Speaker Dependent,SD)系统。

经典的说话人自适应方法可以分为3大类[1]：基于最大后验概率的方法、基于最大似然线性变换的方法和基于说话人聚类的方法，其典型代表分别是最大后验(Maximum A Posteriori, MAP)[1]自适应方法，最大似然线性回归(Maximum Likelihood Linear Regression, MLLR)[2]及本征音(EigenVoice, EV)[3]说话人自适应方法。文献[1]和文献[4]提出了一种基于本征音子(EigenPhone, EP)的说话人自适应方法。与EV方法不同，该方法认为对于每一个说话人，其SD模型中不同高斯分量均值的变化(相对于SI模型)位于一个子空间中，称该子空间为“音子变化子空间(phone variation subspace)”，其基矢量称为“本征音子”，反映了说话人的个体特征，是说话人相关的；而不同高斯分量对应的坐标反映了不同音子之间的相关性信息，是说话人无关的。在训练阶段，可以根据训练数据得到各高斯分量的坐标矢量，在自适应阶段估计未知说话人的本征音子矩阵，即可达到说话人自适应的目的。本征音子自适应方法具有直观的物理意义，在自适应数据充分的情况下，能够得到比MLLR方法和EV方法更好的结果。然而，其缺点是在自适应数据较少的情况下，极易出现严重的过拟合现象。

在语音信号处理与语音识别领域，正则化方法近年来被越来越多地应用于解决数据稀疏问题和降低模型的复杂度。例如，利用L1正则化方法可以得到噪声语音信号的稀疏表达，从而提高噪声条件下的语音识别系统识别率[5]；在子空间 GMM 声学模型中，采用L1和L2正则化方法[6]可以得到具有稀疏性的模型参数，进一步提高少量数据下的声学建模能力；在基于深层神经网络的语音识别系统[7]中，采用 L1正则化方法减少神经网络中的非零权值个数，从而在不牺牲系统识别率的情况下大大降低模型复杂度。

实验证明，在本征音子说话人自适应方法中，本征音子个数应随着自适应数据量的增加而不断增大。由于它决定了音子变化子空间的维数，与本征音子矩阵的秩密切相关，因此可以考虑将本征音子矩阵的秩作为正则项，引入低秩矩阵约束来提高本征音子说话人自适应方法的性能。直接将矩阵的秩作为正则项是无法求解的，在矩阵优化问题中，通常采用核范数作为矩阵秩的一个凸近似，从而将原问题转化为一个凸优化问题进行求解[8]。目前，基于核范数的正则化方法已被应用于矩阵恢复[8]、稳健性主分量分析[9]、图像处理[10]等领域，并取得了不错的效果。本文章节安排如下：第2节简要介绍了本征音子说话人自适应方法，给出了一种快速实现算法；第3节讨论基于核范数正则化的本征音子自适应及其数学优化算法；第4节给出了实验结果及分析；最后给出了本文的结论。

2 本征音子说话人自适应

假设 SI系统中，共M个高斯混元，特征矢量维数为D，令mμ为第m个高斯混元的均值矢量。在第s个说话人的 SD系统中，第m个高斯混元的均值矢量用表示，定义音子变化矢量为。在本征音子说话人自适应中，假设位于一个说话人相关的维子空间中，称该子空间为“音子变化子空间”。设该子空间的原点为，基矢量为，称为第s个说话人的本征音子 EP。令第m个高斯混元对应的坐标矢量为，则在音子变化子空间中可以分解为

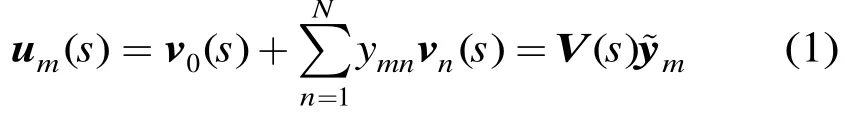
3 基于低秩约束的本征音子说话人自适应

3.1 基于低秩约束的本征音子说话人自适应原理

在文献[4]中，实验表明，在自适应数据量充足时，本征音子自适应方法能够取得很好的自适应效果，随着数据量的增加，本征音子的个数N应逐渐增大；而当数据量不足时，由于无法充分估计本征音子矩阵，会出现严重的过训练现象。为了缓解这一问题，文献[4]引入高斯先验分布，在最大后验准则下得到更为稳健的估计；然而，该方法对识别率的提高有限，只能尽量自适应之后的系统识别率不会下降。本文通过对本征音子矩阵引入低秩约束来解决这一问题。事实上，本征音子的个数N与本征音子矩阵的秩密切相关，引入低秩约束可以有效地限制模型的复杂度，防止过训练问题。

数学上直接将矩阵的秩作为约束条件是无法求解的，通常采用矩阵的核范数(nuclear norm)作为矩阵秩的一个凸近似，从而将原问题转化为一个凸优化问题来求解。对于本征音子矩阵()sV，令为其第i个奇异值，则其核范数为。事实上，用矩阵的核范数来近似矩阵的秩，与压缩感知中常用的以矢量的L1范数来近似其L0范数是类似的：矩阵的秩等于奇异值矢量的L0范数，其核范数就等价于奇异值矢量的L1范数。对目标函数式(4)引入核范数正则项，新的优化问题可以写为

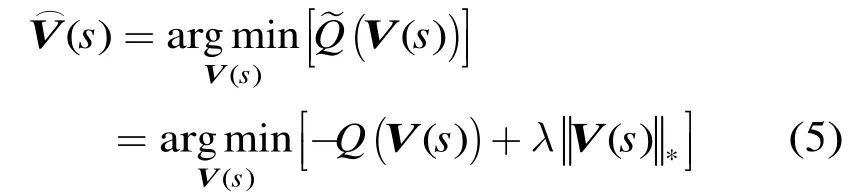
3.2 基于低秩约束的本征音子矩阵优化算法

式(5)是一个凸优化问题，已有多种求解算法，如快速迭代收缩-阈值算法(Fast Iterative Shrinkage-Thresholding Algorithm, FISTA)[12], ADMiRA算法[13]，奇异值阈值法(Singular Value Thresholding,SVT)[14]等。本文采用一种加速近点梯度法(Accelerated Proximal Gradient, APG)[15,16]对其进行求解。

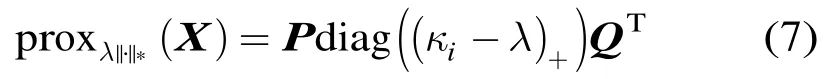
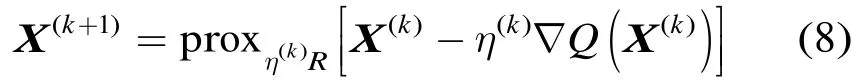
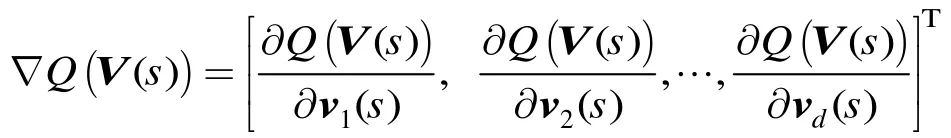
(5)的一个加速近点投影算法流程如下(为了简洁起见，将 ()sV 简记为V)：

(3)计算

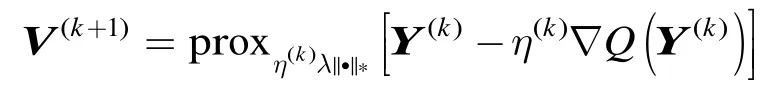
上述算法中，第(2)步采用动量法(momentum method)加快迭代收敛过程。其中，的计算采用了文献[12]中给出的一个经验公式(第(5)步)；在迭代初始时刻(时)，；而在时，。实验证明，这一方法可以明显加快算法的迭代收敛过程。第(3)步即是近点梯度下降法的迭代公式。其中，λ是核范数的权重，是第步的下降步长。这里对采用了一种1维线性搜索的方法：在第(4)步当检测到迭代前后目标函数变大时，按0.8的系数减小步长，重新回到第(3)步进行迭代过程。不难证明，这一步长选择方法满足迭代收敛条件。最后一步，检查迭代前后的相对减少量是否小于，若“是”则停止迭代过程，否则重新回到步骤(2)进行迭代。

4 实验结果及分析

为了验证本文算法的有效性，本节针对一个典型的汉语连续语音识别系统进行了实验。实验数据采用微软语料库[17]，训练集共有 100个说话人，共19688句话，约为 33个小时的数据；测试集共 25个说话人，每人20句话，每句话的平均时长约为5 s。采用典型的 13维美尔频率倒谱系数(Mel-Frequency Cepstrum Coefficients, MFCC)及其一阶和二阶差分系数，总的特征矢量维数为39。基线系统中的说话人无关模型利用 HTK工具包(3.4.1版本)[11]训练得到，采用三音子有调声韵母作为声学建模单元，每个HMM模型含有3个输出状态，每个状态共8个高斯混元，三音子聚类后总的高斯混元数为19136。训练阶段采用基于回归树(32个回归类)的MLLR自适应方法得到100个训练说话人相关模型。识别阶段，以HTK中的HVite工具为解码器进行连续语音识别，采用有调音节全连接的解码网络，不采用语法模型。这种解码网络的系统对声学模型的要求最高，可以更好地测试声学模型自适应的效果。在说话人自适应实验中，对每个测试说话人随机抽取10句话作为自适应数据，用于对SI声学模型进行有监督说话人自适应；将剩下的10句话作为测试数据，在其上统计有调音节的平均正确识别率[18]作为实验结果。在测试数据上，SI模型的平均正确识别率为 53.04%(文献[17]中结果为51.21%)。实验中，本文针对下列说话人自适应算法进行对比实验：

(1)MLLR+MAP：最大似然线性回归(MLLR)后接最大后验估计(MAP)的自适应算法，根据文献[5]中的实验结果，采其最好的实验设置：即对MLLR采用包含 32个回归类的回归树及分块对角变换矩阵，对MAP其先验权重设置为10；

(2)ML-EP：基于最大似然估计的本征音子自适应算法，本征音子个数(N)取50或100；

(4)LR-EP：本文提出的基于低秩约束的本征音子自适应算法，核范数权重(λ)从10调整到200。

其中(1)是目前常用的说话人自适应算法，(2)和(3)是本文作者近期提出的本征音子说话人自适应算法，(4)是本文提出的基于低秩约束的本征音子自适应算法。为了比较各方法在不同自适应数据量下的自适应效果，分别对1句话，2句话，4句话，6句话，8句话和10句话的自适应数据进行了有监督说话人自适应实验。

表1中给出了前3种自适应算法的典型实验结果，每种算法的最好结果在表中以黑体标明。由表1可见，在自适应数据量充足(4≥句话)的情况下，当时，算法的性能优于MAP算法；而当时，其性能下降明显，在句话时均达不到的自适应性能。这是由于对于算法，时要估计的参数数量比时多出一倍，即使数据量为10句话，仍无法得到本征音子矩阵的充分估计，出现过拟合现象。这种现象在数据量少时(2≤句话)尤为明显：无论是还是, ML-EP算法的识别率甚至低于自适应前的SI系统。这一严重的过拟合现象在引入高斯先验分布后得到了一定的缓解。由表1结果可见，MAP-EP算法在1~2句话时通过调整高斯先验分布的方差可以大大提高自适应后的系统正识率：在时，平均正识率分别达到 53.92%和 54.28%；在时，平均正识率也能达到 53.69%和54.28%。这些结果已经接近甚至超出了 MLLR+MAP算法的最好结果(分别为53.32%和54.93%)。然而，在该参数设置下，当自适应数据量充足时(4≥句话)，却制约了 MAP-EP算法的性能；此时，减少的值，可以提高系统的正识率：在时，10句话时平均正识率达到60.70%，其结果略高于MLLR+MAP算法的最好结果。该现象说明，在时，通过引入适当的约束，可以提高系统的自适应性能。

由表2可见，在引入低秩约束后，通过调整核范数的权重，可以使得本征音子自适应算法的效果得到明显提升。当时，在1,2,4,6,8和10句话自适应数据量下，平均正确识别率分别为53.92%, 55.62%, 58.29%, 59.21%,59.95%和60.57%，这些结果均优于ML-EP, MAP-EP及MLLR+MAP的最好结果。当时，在2句话和4句话自适应数据量下，平均正确识别率分别为55.32%和 58.02%，仅略低于时的结果；在1,6,8和10句话自适应数据量下，平均正确识别率分别为54.26%, 59.40%, 60.21%和61.32%，这是相同自适应数据量下所有测试系统中的最好结果。与MAP-EP算法不同，LR-EP算法可以在同一参数设置下(如时，λ取为时，λ取为 120)应对不同的自适应数据量，既不会在数据量少时出现过拟合现象，也不会在数据量充分时出现欠拟合现象。

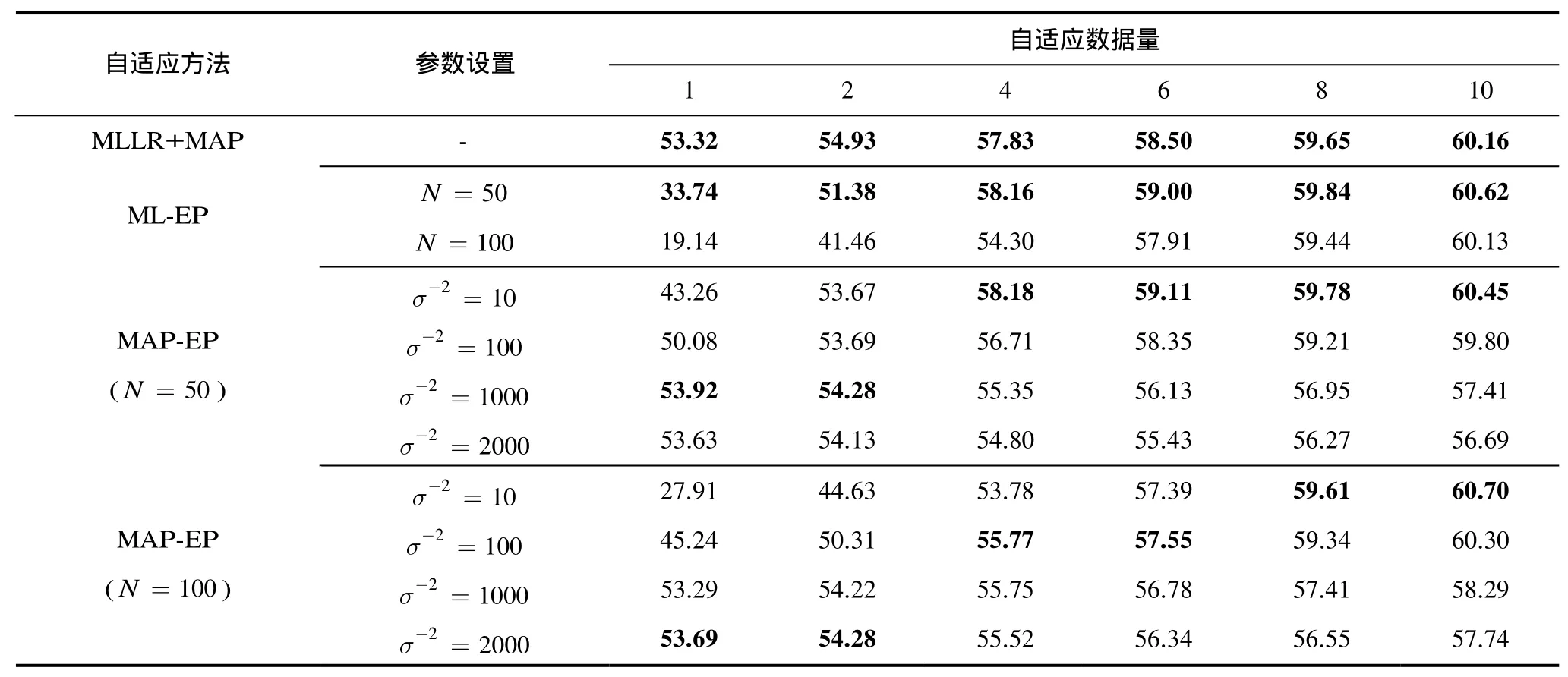
表1 3种已有自适应算法的正确识别率(%)

表2 基于低秩约束的本征音子说话人自适应后平均正确识别率(%)(括号中数字为所有测试说话人本征音子矩阵秩的平均值)

由表2可以看出，本征音子矩阵的秩随着核范数权重λ的变化而不同。在相同的自适应数据量下，随着λ的增大，本征音子矩阵的秩随之增大；而在相同的权重(λ)设置下，随着自适应数据量的增加，本征音子矩阵的秩也随之增大，此结果与理论分析相吻合；随着自适应数据量的增加，更多的参数可以得到稳健的估计，应该增大音子变化子空间的维数，而音子变化子空间的维数与本征音子矩阵的秩是等价的。对比和时的结果可见，两种参数设置下，对于各种自适应数据量所得到的本征音子矩阵的秩几乎是相同的，两种参数设置均找到了各种自适应数据量下的本征音子矩阵秩的最佳值；相比而言，时的结果比时的结果略好，这可能是由于随着N的增大，每个高斯混元的坐标矢量my 的维数增加，对音子变化子空间的描述更为精确，从而使得系统具有更强的自适应能力。

在上述实验中，由于实验语料的限制，本文在测试集上通过调整参数N及λ以得到最佳的识别效果，并将其与其它方法的最佳结果相比较以体现新方法的优越性。在实际应用中，应建立一个独立于训练集数据之外的开发集数据，调整参数N及λ，将开发集上识别率最高时对应的参数作为其最佳取值。

5 结论

本文提出了一种基于低秩约束的本征音说话人自适应方法。新方法在本征音子矩阵估计过程中，引入低秩约束，用矩阵的核范数作为其秩的一个凸近似，对优化的目标函数引入带有核范数的正则项，并采用加速近点梯度算法得到本征音子矩阵的迭代优化算法。引入低秩约束后，可以有效地对自适应模型的复杂度进行控制，在数据量少时得到低维音子变化子空间，在数据量充足时得到高维音子变化子空间。实验证明，新算法在各种自适应数据量下均优于经典的 MLLR+MAP自适应算法及原始的本征音子自适应算法。

[1] Zhang Wen-lin, Zhang Wei-qiang, Li Bi-cheng, et al..Bayesian speaker adaptation based on a new hierarchical probabilistic model[J]. IEEE Transactions on Audio, Speech and Language Processing, 2012, 20(7): 2002-2015.

[2] Zhang Shi-lei and Qin Yong. Model dimensionality selection in bilinear transformation for feature space MLLR rapid speaker adaptation[C]. Proceedings of International Conference on Acoustics, Speech, and Signal Processing,Kyoto, Japan, 2012: 4353-4356.

[3] 张文林, 牛铜, 张连海, 等. 基于最大似然可变子空间的快速说话人自适应方法[J]. 电子与信息学报, 2012, 34(3): 571-575.Zhang Wen-lin, Niu Tong, Zhang Lian-hai, et al.. Rapid speaker adaptation based on maximum-likelihood variable subspace[J]. Journal of Electronics ＆amp; Information Technology, 2012, 34(3): 571-575.

[4] Zhang Wen-lin, Zhang Wei-qiang, and Li Bi-cheng. Speaker adaptation based on speaker-dependent eigenphone estimation[C]. Proceedings of IEEE Automatic Speech Recognition and Understanding Workshop, Hawaii, USA,2011: 48-52.

[5] Gemmeke J and Van hamme H. Advances in noise robust digit recognition using hybrid exemplar-based techniques [C].Proceedings of Interspeech, Oregon, Portland, 2012.

[6] Lu L, Ghoshal A, and Renals S. Regularized subspace Gaussian mixture models for speech recognition[J]. IEEE Signal Processing Letters, 2011, 18(7): 419-422.

[7] Yu D, Seide F, Li G, et al.. Exploiting sparseness in deep neural networks for large vocabulary speech recognition[C].Proceedings of International Conference on Acoustics, Speech,and Signal Processing, Kyoto, Japan, 2012: 4409-4412.

[8] Deledalle C, Vaiter S, Peyre G, et al.. Risk estimation for matrix recovery with spectral regularization[OL]. http://arxiv.org/abs/1205.1482, 2012.

[9] Candes E J, Li X, Ma Y, et al.. Robust principal component analysis?[J]. Journal of ACM, 2011, 58(3): DOI: 10.1145/1970392. 1970395.

[10] Chen Chih-fan, Wei Chia-po, and Wang Y C F. Low-rank matrix recovery with structural incoherence for robust face recognition[C]. Proceedings of Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 2012: 2618-2625.

[11] Young S, Evermann G, Gales M, et al.. The HTK book (for HTK version 3.4)[OL]. http://htk.eng.cam.ac.uk/docs/docs.shtml. 2009.

[12] Beck A and Teboulle M. A fast iterative shrinkagethresholding algorithm for linear inverse problems[J]. SIAM Journal on Imaging Sciences, 2009, 2: 183-202.

[13] Lee K and Bresler Y A. Atomic decomposition for minimum rank approximation[J]. IEEE Transactions on Information Theory, 2010, 56(9): 4402-4416.

[14] Cai J, Candes E, and Shen Z. A singular value thresholding algorithm for matrix completion[J]. SIAM Journal on Optimization, 2010, 20(4): 1956-1982.

[15] Toh K C and Yun S. An accelerated proximal gradient algorithm for nuclear norm regularized linear least squares prolems[J]. Pacific Journal of Optimization, 2010, 6(3):615-640.

[16] Parikh N and Boyd S. Proximal algorithms[J]. Foundations and Trends in Optimization, 2013, 1(3): 123-231.

[17] Chang E, Shi Y, Zhou J, et al.. Speech lab in a box: a Mandarin speech toolbox to jumpstart speech related research[C]. Proceedings of Eurospeech, Scandinavia, 2001:2799-2802.