基于优化概率神经网络和红外多光谱融合的大气层外空间弹道目标识别

张国亮杨春玲王暕来

①(哈尔滨工业大学电气工程及自动化学院 哈尔滨 150001)②(中国运载火箭技术研究院 北京 100076)

1 引言

在自动目标识别(Automatic Target Recognition, ATR)研究领域，大气层外空间弹道目标的自动识别是一个挑战性的难题[1]。这主要是因为空间弹道目标的自动识别具有如下难点：(1)弹道目标存在多样性，包括弹头，导弹碎片以及诱饵(可能又包含重诱饵和轻诱饵)等；(2)弹道目标的辐射特性表现出动态时变性；(3)远距离探测时，获取目标的信息量非常有限。这些难点反应在实际应用中主要就是如何提取用于目标识别的有效特征以及如何设计有效的目标分类算法。针对空间目标识别的这些问题，很多学者进行了此方面的研究[24]-。文献[2-4]中的方法主要是利用雷达的时频域量测特征进行的目标识别，其中主要包括目标的雷达散射截面积(Radar Cross Section, RCS)，目标的运动轨迹，以及目标的多普勒特征等。但当有多个真假目标同时在中段飞行时，弹头并不存在区别其它诱饵的固有频率，而且弹头和诱饵的轨迹相近[5]，这给弹道目标的识别造成很大困难。光谱信息是由物体内在的物理性质决定的，所以通过分析物体光谱信息，可以获得其它方法不能获得的目标固有属性。因此目标的光谱差异信息可以作为识别目标的一种重要手段。另外，由于人工神经网络良好的并行性和自学习能力，近年来被广泛用于空间弹道目标识别。文献[6]设计了三波段的空间弹道目标识别算法，采用反向传播(Back Propagation, BP)神经网络对空间弹道目标进行了识别。文献[7]利用双波段红外辐射特性提出了一种时延回归神经网络(Time-Delay Recurrent Neural Network, TDRNN)用于空间弹道目标识别。文献[8]利用目标的红外特性提出一种时延神经网络(Time-Delay Neural Network, TDNN)弹道目标识别方法。文献[9]提出了一种自适应时延神经网络(Adaptive Time-Delay Neural Network,ATNN)识别大气层外弹道目标。通过分析可知，TDNN在空间目标识别中较为常用，如 ATNN和TDRNN就是TDNN的变种。但TDNN本质上和BP极为相似，属于BP神经网络的“增强版”[8]。BP类神经网络的学习和记忆具有不稳定性，即如果增加学习样本，训练好的网络需要从头重新训练，对以前网络的权值和阈值没有记忆，且易陷入局部极小值。另外上述神经网络学习算法复杂度较高，这可能会限制它们在实际中的应用。

概率神经网络(Probabilistic Neural Network,PNN)近年来已在不同模式识别领域得到应用[10,11]，因为PNN具有学习过程简单，收敛于贝叶斯最优解等优点。另外，近年来多光谱红外数据在ATR领域表现出极大的潜力，主要是它们可同时提供目标的时域特征和光谱特征。因此利用多光谱数据融合目标的时谱特性可能会进一步提高目标识别性能。本文就是从多光谱数据融合的优势出发，通过对大气层外空间弹道目标的多光谱红外辐射序列的仿真和实验研究，提出一种基于粒子群优化PNN的空间弹道目标识别方法。该方法通过融合弹道目标的多光谱红外辐射数据，提高了目标识别的稳健性，利用提出的多比色测温方法提高了动态特征提取的精确度。文中首先介绍了PNN模型及其学习算法。其次采用粒子群优化方法对PNN进行优化。然后提出一种基于比色测温的多色测温方法对空间弹道目标的动态特征进行提取。最后利用仿真实验数据对4类典型空间弹道目标进行了识别研究。

2 概率神经网络模型

PNN是由径向基神经网络发展而来的一种前馈型神经网络，最早由Specht[12]提出。其基本原理为假设有d维输入特征向量，它属于c个分类之一。和分别为类iω的先验概率和类条件概率密度函数(似然函数)。贝叶斯决策理论通过最小化总风险做出相应决策，如果正确分类损失为0，错误分类损失为1，即损失函数为0-1函数，其判决规则为

式(2)的iN是类iω的训练样本个数，为类iω的第j个训练样本，σ为平滑因子。

PNN模型包括输入层、模式层、求和层和输出层4部分。输入层神经元个数与特征矢量x的维数相等，该层负责接收测试集的样本并将该样本的特征矢量传递给网络。模式层含有c组神经元(每组神经元对应一个模式类)，每组神经元的个数与训练集该类别的样本数相同，该层负责计算特征矢量x与训练集各个样本的匹配关系，因而每个神经元都与输入层完全连接，第i组第j个神经元的输出为

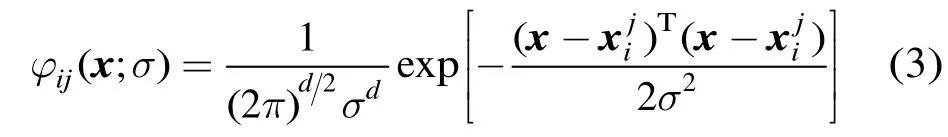
其中是类iω的第j个训练样本，同时也是该神经元的权值向量。求和层含有c个神经元(每个神经元对应一个模式类)，每个神经元只与属于自己类别的模式层神经元相连，将模式层所有该类神经元的输出累积后取均值，得到

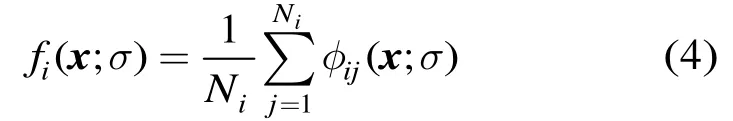
由式(4)可知，求和层各神经元的输出与类条件概率密度函数的Parzen窗估计相等。输出层含有c个神经元(每个神经元对应一个模式类)，该层负责接收求和层输出的各类别条件概率密度函数，每个神经元的输出为

需要指出的是，在仿真实验中平滑因子σ对PNN的性能有一定的影响。平滑因子较小时会造成网络的过拟合，易受噪声干扰。虽σ越大时逼近函数越平滑，但σ过大会造成模式层的神经元个数过多，进而增加计算量。因此应用PNN的关键是如何选取合适的σ值。

3 高斯粒子群优化PNN

粒子群优化算法(Particle Swarm Optimization,PSO)是一种基于种群智能方法的演化计算技术[13]。PSO具有收敛速度快、算法简单等优点，而且它不要求被优化函数具有可导、可微等性质。由于经典的 PSO算法严重依赖加速度常数和惯性权值的设置，本文拟采用一种高斯粒子群优化(Gaussian PSO,GPSO)[14]方法对PNN的σ值进行优化。

设粒子群数目为N，第n个粒子在D维空间中的位置和速度分别为和代表粒子n的历史最好位置(最好拟合值的位置)，是第n个粒子所在邻域的历史最佳位置(通常将邻域选为整个种群，即全局模型)。粒子速度迭代方程为

其中k为种群代数(或迭代次数)。|rand|和|Rand|是正随机数，可由高斯概率密度的绝对值产生，即abs[(0,1)]N ，其中 (0,1)N 表示零均值、单位方差的标准正态分布。

粒子的位置更新方程为

式(8)中粒子速度和位置都是随机矢量。式(7)和式(8)显示GPSO只需要用户设置粒子数N，不需要别的参数。

本文计算每一个网络在训练集上产生的均方误差，并以此作为目标函数。通过目标函数构造相应的适应度函数，用来计算每个粒子的适应度。目标函数为

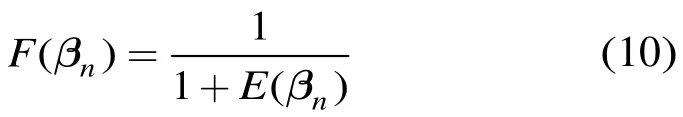
综上所述，本文提出的高斯粒子群优化 PNN(GPSO-PNN)算法流程如下：(1)训练集中的样本都归一化为单位长度，即；(2)将 PNN 的目标函数设置为GPSO的目标函数，进而求得适应度函数，即式(10)；(3)将 PNN 中的待优化参数写为GPSO的粒子位置；(4)初始化GPSO中的主要参数，限定粒子的搜索空间，并确定算法的终止条件；(5)利用归一化训样本训练每个 PNN。运行GPSO算法，按式(7)和式(8)更新，直到满足终止条件；(6)如果终止条件不满足，返回到第(4)步；(7)返回粒子群全局最优值gp作为平滑因子的最优值，并利用此值进行实验得到最终识别结果。

4 大气层外空间弹道目标的动态特征提取

通过大量的仿真实验研究，我们决定将温度变化率和有效辐射面积变化范围作为空间目标识别的有效特征。当前空间目标的温度测量通常采用比色测温法[15]。假设绝对温度为T的空间目标在红外探测系统处产生的辐照度为

式(12)中1c和2c是辐射常数。当时，式(12)可以近似表示为

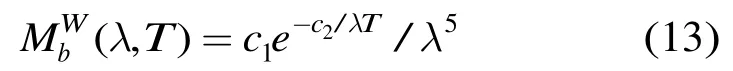
式(13)又称为维恩辐射定律。对于比色测温，结合式(11)和式(13)，在假设的情况下，双波段比色测温法可表示为

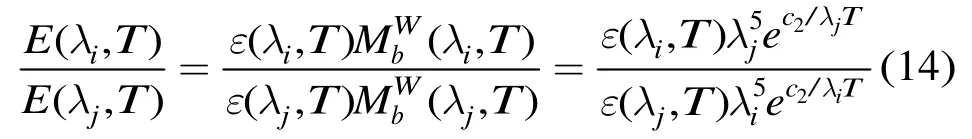
整理式(14)后得到

在传统的多光谱辐射测温方法中，发射率通常用一个含有未知参数的关于波长的平滑函数来描述。为此，本文将式(17)中发射率比的自然对数用一个关于波长的多项式函数来描述，即

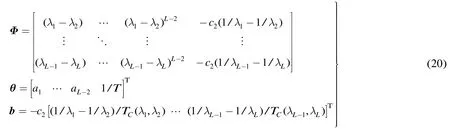
误差函数一般用误差平方和来表示，即

通过减小未知目标发射率的不确定性，上述方法能够进一步提高温度测量的精确度。一旦获取了空间目标的绝对温度，利用空间目标测轨所提供的距离信息，还可以得到另一个识别特征量目标的有效辐射面积，由式(11)可得

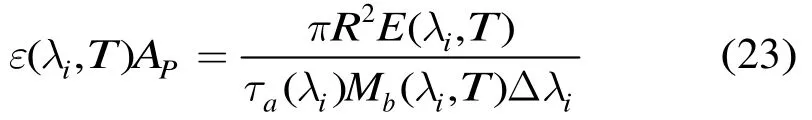
5 仿真实验数据及目标识别结果

红外探测器接收到的目标信号强度受诸多因素的影响(如目标动力学特性，表面温度，有效辐射面积，目标距探测器距离等)，因此很难精确描述目标的红外辐射强度。目标信号时间序列的仿真只能依托于某些特定模型，其中较为常用的是 BODE(Bhattacharyya Optical Decoy Evaluation)模型。利用简化后的二阶BODE模型，则t时刻目标在第l个波段的相对光谱辐照度可以表示为

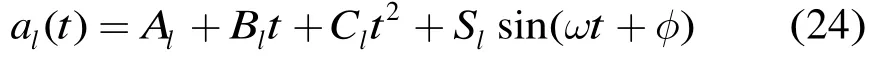
其中lA,lB和lC分别代表目标相对光谱辐照度在该波段随时间零次项，一次项和二次项的变化程度；和φ分别为正弦调制项的幅值，角速度和初相角，以上3个参数用于描述空间目标的进动运动对目标相对光谱辐照度造成的影响，因此对某一特定目标而言，ω和φ在各个波段的值是相同的。认为是均值为0的加性噪声。第i波段的信噪比(单波段信噪比)SNR定义为正弦调制项幅值lS与噪声方差的比值。

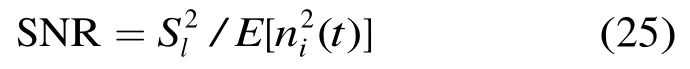
根据BODE模型和表1中的参数，4种典型空间目标某波段的相对光谱辐照度随时间的变化曲线如图1所示，这里的单波段信噪比SNR=1。本文采用12个光谱波段数据做测试，这些波段均匀地分布在4~15μm。

根据上述仿真实验数据，利用本文提出的多比色测温法可以很容易地提取出该目标的动态温度。图2比较了两种不同测温法提取出的目标温度与目标原始温度的差异，其中前者为传统的双色测温法，后者为本文提出的多比色测温法。观察图2可以发现，相比传统的双色测温法，多比色测温法的测量误差更小。因此多比色测温方法进一步提高了温度测量的准确性。

为衡量两个时变特征对弹头、重诱饵、导弹碎片以及气球诱饵4种典型空间目标的识别能力，我们给出了上述4种目标针对每个特征的概率密度函数，如图3(a)和图3(b)所示。这里把目标特征随时间的变化曲线视为该目标特征的概率密度函数，从而可以利用其差异达到识别目标的目的。观察上述两图可以发现，以上4种空间目标的概率密度函数差异明显，因此利用上述两个时变特征可有效对目标进行区分。由于重诱饵和弹头在形状上相似，本文将详细阐述利用上述特征识别弹头和重诱饵的有效性。尽管重诱饵初始释放温度跟弹头相近或者相同，但重诱饵的温度变化率大于弹头，也就是说重诱饵的温度相比弹头下降要快。另外，重诱饵不可能做到和弹头一模一样，且往往由于实际条件的限制其尺寸和重量比弹头小的多，因此重诱饵的有效辐射面积变化范围通常是小于弹头的。因此利用上述特征可对弹头和重诱饵有效区分。

表1 空间目标的基本物理参数

图1 利用BODE模型生成的目标相对光谱辐照度(SNR=1)

图2 原始温度与预测温度的比较

图3 4种典型空间目标特征的概率密度函数

训练数据集共有400个样本数据，其中弹头、重诱饵、导弹碎片和气球诱饵各100个。将提取出的目标时变温度和时变有效辐射面积以0.5 s的时间间隔进行采样，共持续 5 s，即每个动态特征均有11个样本点用于构建其概率密度函数，将22维的特征矢量送入 GPSO-PNN神经网络进行训练，具体训练过程参见本文第3节。由于本文使用了GPSO技术对PNN优化，不需要反复手动调节PNN的平滑因子。

本文比较了不同单波段信噪比条件下采用GPSO-PNN神经网络和BP神经网络进行目标识别的结果，如表2所示。其中W, HD, F和BD分别代表弹头、重诱饵、导弹碎片和气球诱饵，其余参数设置同前。表2的识别结果证明本文提出的方法对4类典型空间目标是有效的。另外观察表2可以发现，在低信噪比条件下，与传统 BP神经网络相比，GPSO-PNN神经网络能够获得更好的分类识别性能。

6 结论

本文提出了一种基于优化概率神经网络和多光谱红外数据融合的方法用于大气层外空间弹道目标的识别。该方法充分融合了多光谱红外数据的时间信息和光谱信息，在此基础上提出了一种基于比色测温的多色测温方法用于提取目标的动态特征，提高了温度测量的精确度，进而提高了目标识别的准确率。利用PNN训练得到各模式类的后验概率，优于传统的硬性判决。针对PNN中的平滑因子选取问题，本文采用GPSO优化方法进行了优化，避免了手动操作。利用仿真实验数据进行了测试，并比较了不同单波段信噪比条件下的平均识别成功率。仿真结果显示在低信噪比条件下，本文算法的识别性能优于传统的BP神经网络。

表2 GPSO-PNN和BP两类识别方法的结果比较

[1] 高乾, 周林, 王森, 等. 弹道导弹中段目标特性及识别综述[J].装备指挥技术学院学报, 2011, 22(1): 78-82.Gao Qian, Zhou Lin, Wang Sen, et al.. Summarize of target characteristics and recognition of ballistic missile in trajectory midcourse[J]. Journal of the Academy of Equipment Command ＆amp; Technology, 2011, 22(1): 78-82.

[2] 范成礼, 邢清华, 付强, 等. 基于直觉模糊核聚类的弹道中段目标识别方法[J]. 系统工程与电子技术, 2013, 35(7):1362-1367.Fan Cheng-li, Xing Qing-hua, Fu Qiang, et al.. Technique for target recognition in ballistic midcourse based on intuitionistic fuzzy kernel clustering[J]. Systems Engineering and Electronics, 2013, 35(7): 1362-1367.

[3] 寇鹏, 刘永祥, 朱得糠, 等. 基于轨迹特性的中段目标识别方法[J]. 宇航学报, 2012, 33(1): 91-99.Kou Peng, Liu Yong-xiang, Zhu De-kang, et al..Discrimination strategy for midcourse target based on trajectory characteristics[J]. Journal of Astronautics, 2012,33(1): 91-99.

[4] 田巳睿, 蒋跃红, 郭汝江, 等. 基于时频变换的弹道目标微多普勒特征提取[J]. 现代雷达, 2012, 34(1): 40-43, 48.Tian Si-rui, Jiang Yue-hong, Guo Ru-jiang, et al.. Ballistic target micro-doppler feature extraction method based on the time-frequency analysis[J]. Modern Radar, 2012, 34(1): 40-43,48.

[5] 武春风, 张伟, 李洁, 等. 基于时空信息的红外成像系统在探测识别目标时所面临的问题及分析[J]. 光学技术, 2005, 31(2):231-234.Wu Chun-feng, Zhang Wei, Li Jie, et al.. Problems and its analysis of infrared imaging detection and identification facing[J]. Optical Technique, 2005, 31(2): 231-234.

[6] Haberstroh R and Kadar I. Multispectral data fusion using neural networks[C]. Conference on Signal Processing, Sensor Fusion, and Target Recognition, Orlando, USA, 1993: 65-75.

[7] 刘涛, 吕江北, 王书宏, 等. 基于TDRNN的大气层外弹道式空间红外目标识别[J]. 电子与信息学报, 2010, 32(1): 80-85.Liu Tao, Lü Jiang-bei, Wang Shu-hong, et al.. Exoatmospheric discrimination of infrared ballistic space target based on the time-delay recurrent neural network[J]. Journalof Electronics ＆ Information Technology, 2010, 32(1): 80-85.

[8] Resch C. Exo-atmospheric discrimination of thrust termination debris and missile segments[J]. Johns Hopkins APL Technical Digest, 1998, 19(3): 315-321.

[9] Lin D T. Target components discrimination using adaptive time-delay neural network[J]. Journal of Information Science and Engineering, 2004, 20(5): 959-980.

[10] 李新德, 杨伟东, Dezert Jean. 一种飞机图像目标多特征信息融合识别方法[J]. 自动化学报, 2012, 38(8): 1298-1307.Li Xin-de, Yang Wei-dong, and Dezert Jean. An airplane image target’s multi-feature fusion recognition method[J].Acta Automatica Sinica, 2012, 38(8): 1298-1307.

[11] 高志华, 贲可荣, 章林柯. 一种基于直推置信的遗传优化概率神经网络[J]. 南京大学学报(自然科学), 2012, 48(1): 48-54.Gao Zhi-hua, Ben Ke-rong, and Zhang Lin-ke. An optimized probabilistic neural network based on transductive confidence[J]. Journal of Nanjing University (Natural Sciences), 2012, 48(1): 48-54.

[12] Specht D F. Probabilistic neural networks[J]. Neural Networks, 1990, 3(1): 109-118.

[13] Kennedy J and Eberhart R. Particle swarm optimization[C].Proceedings of the IEEE International Conference on Neural Networks, Piscataway, USA, 1995, 4: 1942-1948.

[14] Krohling R A. Gaussian swarm: a novel particle swarm optimization algorithm[C]. Proceedings of the IEEE Conference on Cybernetics and Intelligent Systems,Singapore, 2004: 372-376.

[15] 李云红, 王瑞华, 李禹萱. 双波段比色测温技术及实验测试[J].激光与红外, 2013, 43(1): 71-75.Li Yun-hong, Wang Rui-hua, and Li Yu-xuan. Dual waveband colorimetric temperature measurement technology and experiment[J]. Laser ＆amp; Infrared, 2013, 43(1): 71-75.