低复杂度迭代干扰消除的OFDMA初始测距算法

夏玉杰任光亮

①(西安电子科技大学综合业务网理论及关键技术国家重点实验室 西安 710071)②(洛阳师范学院 洛阳 471022)

1 引言

正交频分多址(Orthogonal Frequency Division Multiple Access, OFDMA)将正交频分复用和多址技术相结合，允许多个用户同时共享有限的频谱资源，已成为第4代移动通信系统的物理层核心技术之一。在IEEE802.16m标准[1]中，将用户无线接入中所涉及的多用户检测和多参数估计等处理定义为初始测距，利用初始测距实现接入用户检测、上行链路同步和发送功率调整等功能。

按照IEEE802.16标准[1]的初始测距定义，在一个测距时隙允许多个测距用户(Ranging Subcribe Station, RSS)占用相同的测距子信道同时接入网络，不同用户的测距子信道具有不同的频率选择性，而信道的频率选择性使多用户干扰进一步增大，因此测距子信道的频率选择性和多用户接入干扰(Multiuser Access Interference, MAI)严重影响OFDMA系统初始测距性能。时域/频域相关初始测距算法[26]-把信道频率选择性增大的MAI当做噪声处理，导致测距性能严重恶化。为了减小信道频率选择性对测距性能的影响，文献[7-10]将测距信道分为若干个测距子信道，每个测距子信道由若干个测距子载波构成；这样大大地减小了频率选择性对测距子信道的影响，但测距子信道中测距子载波数目较少，其多用户检测和参数估计要求的工作信噪比高，无法满足小区边缘用户接入需求，且该测距信道分配方案不符合IEEE802.16标准。针对IEEE802.16标准中测距信道分配方案，文献[11-15]提出了基于连续干扰消除的初始测距算法。文献[11]利用串行干扰消除(Serial Interference Cancellation,SIC)方法针对频域检测算法进行改进，该算法在一定程度上提高了多用户检测概率，但由于没有信道估计，干扰消除导致的差错传播和残留的MAI使检测性能明显恶化。文献[12]提出了性能优良的连续多用户检测(Successive MultiUser Detection, SMUD)干扰消除算法，利用最大功率准则搜索测距信号的有效路径，估计该有效径的信道系数，通过信号重构和连续干扰消除，较好地克服了信道频率选择性影响，但该算法复杂度很高，不能满足实时检测要求。文献[13]提出基于测距信号预编码的SMUD算法，该方案能够提高测距检测性能和增加测距用户容量，但计算复杂度仍然很高。为降低SMUD算法的复杂度，文献[14]在迭代过程中按活动测距用户进行干扰消除，但累积的残留MAI极大地限制初始测距性能提升。为提高文献[14]的参数估计精度，文献[15]提出了基于似然比准则的两阶段干扰消除算法，在第1阶段利用测距用户干扰消除[14]获得测距参数，在第2阶段对检测到的测距码集结合并行干扰消除(Parallel Interference Cancellation, PIC)重新检测。由于采用两阶段干扰消除，该算法计算复杂度很高，且检测性能受限于第 1 阶段检测，随着测距用户数增加性能急剧下降。

针对现有算法检测性能不佳以及复杂度过高的问题，本文提出一种低复杂度的迭代并行干扰消除(Iterative PIC, IPIC)初始测距算法。在接收端首先利用自适应门限并行检测活动测距用户的强功率有效径，估计有效径初始参数，利用这些初始估计参数，减小有效径信道系数在估计中的相互干扰，提高有效径参数估计的精度，然后重构和迭代并行消除有效径信号。所提算法在迭代过程中并行检测活动用户的有效径，利用有效径初始参数估计减小信道估计中的互干扰，提高了多用户初始测距性能；通过重构和并行消除有效径测距信号，有效地降低了计算复杂度。

2 初始测距信号模型

假设OFDMA上行链路有N个子载波，按照IEEE 802.16m标准[1]的测距信道分配方案，初始测距时隙由1个测距信道和2个OFDMA符号组成。测距信道在频域上占用6个测距子信道，每个测距子信道包含24个非连续子载波，则测距信道由个子载波组成，分配给测距用户的初始测距子载波集合为。当测距用户完成下行同步以后, 在测距时隙集合中随机选择一个测距时中随机选择一个测距码, 在测距信道上传输。设第u个隙， 从cN 个初始测距码集测距用户选取测距码，则在频域上测距码与子载波间的映射关系为

经N点逆离散傅里叶变换(Inverse Discrete Fourier Transform, IDFT)和插入循环前缀/后缀(Cyclic Prefix, CP)后，将测距码信号调制到两个具有相位连续的OFDMA符号上，则用户u发送的时域测距信号为

其中gN为CP长度。

在初始测距过程中，由于每个测距用户在小区中位置的随机性，基站(Base Station, BS)接收到的初始测距信号将受电磁波往返时延(定时偏差)的影响。最大传输时延对应于测距用户位于小区边缘，则测距用户的最大定时偏差为，其中R为已知的小区半径，c为光速，sT为采样间隔。假定测距用户的信道冲激响应在测距时隙内不变，第u个测距用户的定时偏差为ud。当一个测距时隙内有RK 个测距用户同时接入时，BS接收到的第n个采样信号为

在 BS端，去除 CP和经过离散傅里叶变换(Discrete Fourier Transform, DFT)后，第个测距子载波上输出为

其中。

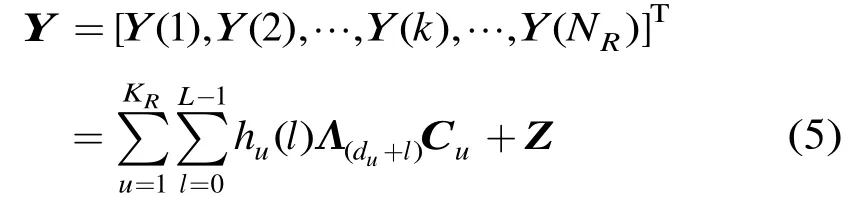
3 低复杂度的迭代干扰消除测距算法

SMUD算法[12]按照最大功率准则，遍历搜索测距用户的最强有效径信号，导致复杂度随测距用户数指数增加；在SIC迭代过程中，由于有效径信道系数估计受到MAI干扰，造成SIC过程中发生误差传播，导致检测性能下降。针对SMUD算法存在的问题，本文提出了迭代并行干扰消除多用户初始测距新算法。该算法在迭代过程中，利用自适应门限并行检测活动测距用户的强功率径，估计有效径初始参数，并利用这些参数减小信道系数估计中有效径之间的相互干扰，然后重构和并行消除有效径信号，从而提高多用户检测性能和降低计算复杂度。

3.1 迭代PIC的多用户检测

为了确定该强径是否为有效路径，取自适应门限[12]为，其中fap 为系统所能接受的虚警概率。

第i次迭代的并行检测结束，获得dN 个有效径的时偏和初始信道系数估计，其中表示第q个有效径的测距码索引。利用有效径初始估计参数，减小有效径信道系数在估计中的相互干扰，更新有效径信道系数估计，详细描述见3.2节。

(3)信号重构和并行干扰消除：重构检测到的有效径信号，然后从接收信号中减去该信号，则用于第i+1次迭代的测距信号为

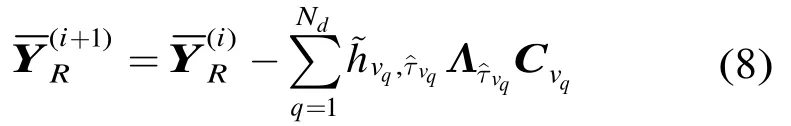
转到步骤(2)继续下一次迭代处理。

第i次IPIC的多用户检测算法是整个算法的核心，其流程如图1所示。在并行检测过程中，按照最大功率准则，对所有个初始测距码与第i次观测信号进行频域相关检测。当所有个相关峰值均小于门限时，表明没有检测到活动的测距用户，迭代结束；当某个相关峰值大于等于门限时，则该测距码的强功率径信号为有效径信号，估计有效径的时偏和初始信道系数。当第i次迭代的并行检测结束，获得个有效径的初始参数估计,。利用有效径初始估计参数，减小有效径信道系数在估计中的相互干扰，然后重构检测到的有效径信号，并从接收信号中并行减去有效径信号。

3.2 有效径间互干扰抵消的信道估计

图1 第i次IPIC多用户检测算法流程

则第r个参考测距码的相关输出为

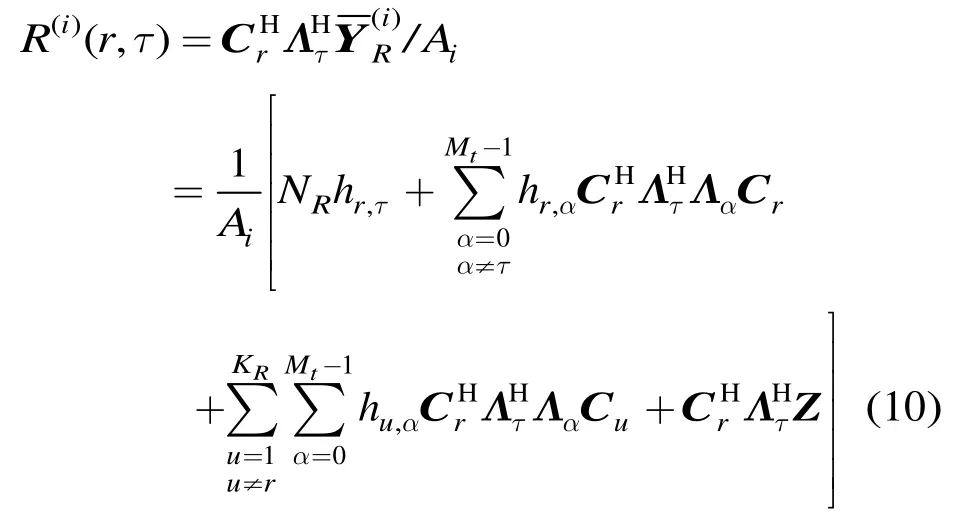
其中，第1项为期望的最强功率径信号，第2项为期望用户的多个时延信号导致的自干扰，第3项为多用户干扰(MAI)，第4项为噪声干扰。

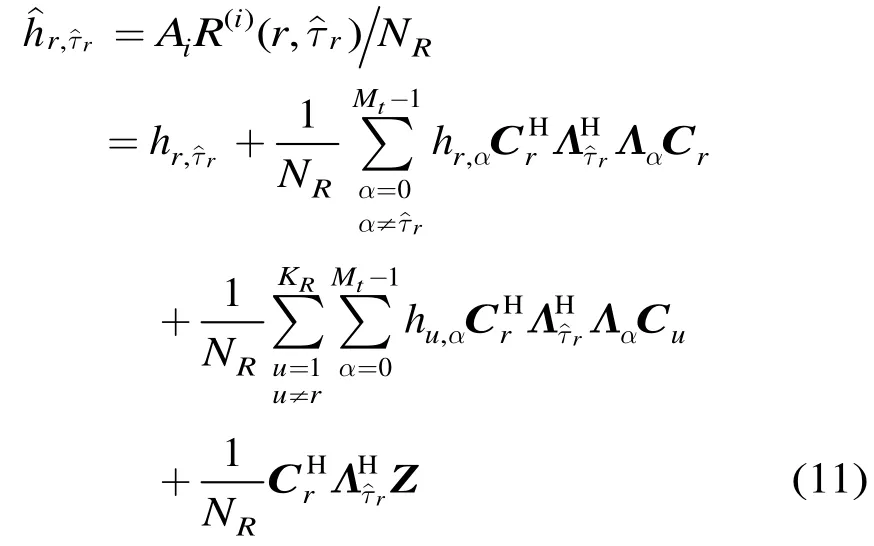
第i次迭代的并行检测过程结束，对所有cN个参考测距码，检测到dN个活动测距用户，其个有效径的初始参数估计集合为。由式(11)看出，各测距用户的初始信道系数估计受到其它用户的MAI干扰。式(11)可以重新表示为

利用dN个有效径参数估计，假定为第i次迭代的第1q-次干扰消除后的有效径信道系数估计，构造已估计有效径对第q次有效径信道估计系数的干扰，再从第q次有效径的信道估计系数中消除干扰，得到该有效径的新估计为

4 性能分析

4.1 信道系数估计分析

根据式(13)，第i次迭代的第q个有效径信道系数估计误差为

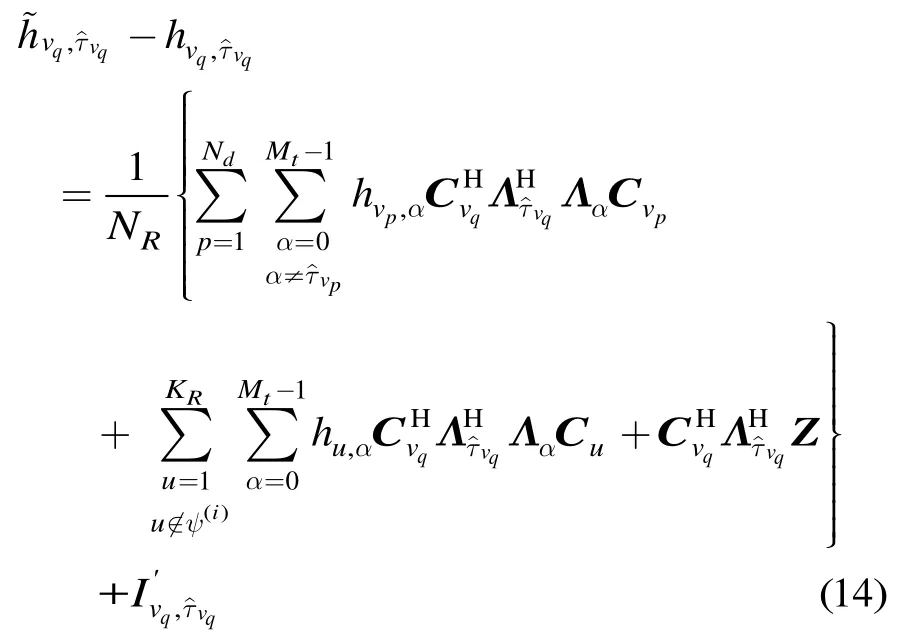
对SMUD，第i次迭代的第q个有效径信道系数估计误差为

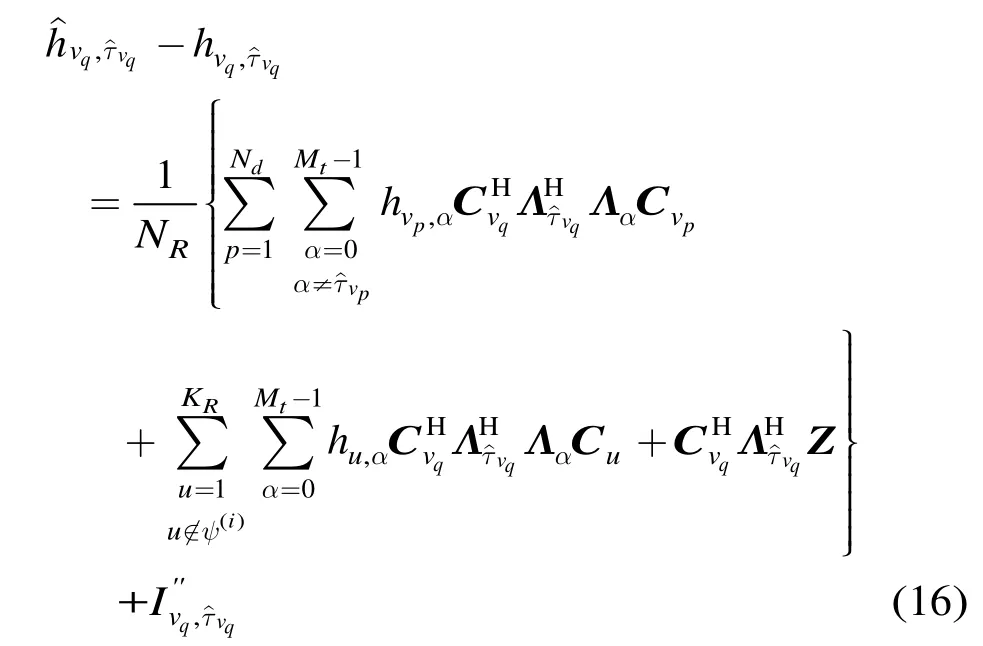
道系数估计的MSE为

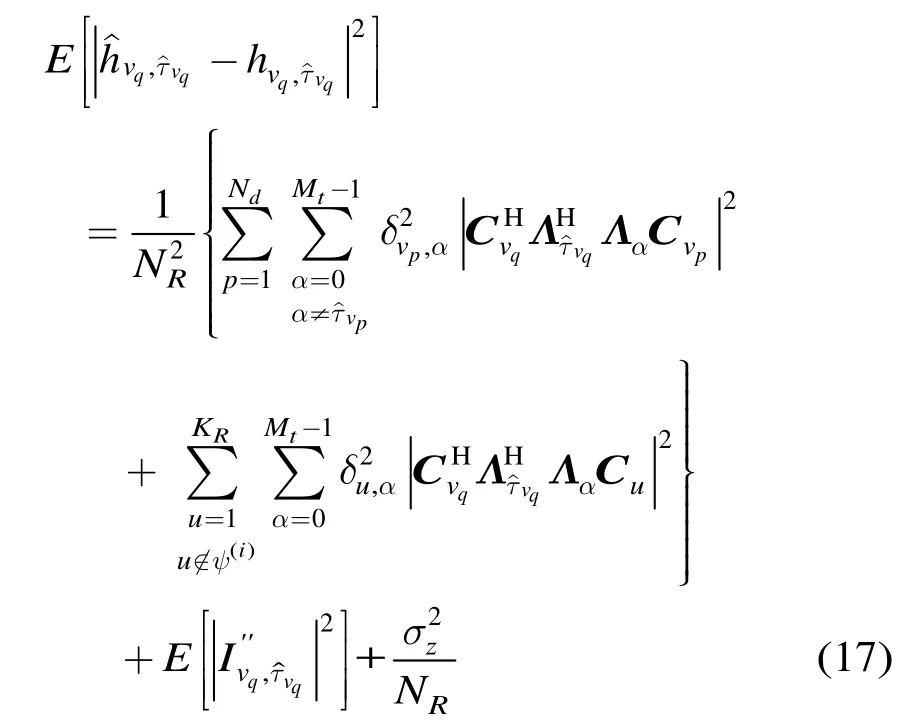
由式(15)，式(17)和式(18)知，本文提出的IPIC算法有效径信道系数估计的MSE精度比SMUD高。因此利用有效径初始估计参数减小有效径信道系数在估计中的相互干扰，能够更好地减小差错传播和残留MAI，提高测距检测性能。

4.2 迭代次数与测距性能分析

本文提出的 IPIC算法的检测性能与迭代次数有关。迭代终止的条件有两个，第1个是测距信号所有可能径的相关值都小于自适应门限时，迭代终止；第2个条件是迭代抵消后信号的功率大于抵消前信号的功率，迭代终止。两个条件确保迭代过程是收敛的，按照所要求虚警率检测出活动测距用户的有效径。在迭代过程中，干扰抵消的效果受到活动用户有效径系数估计精度的影响，精度越高，抵消效果越好，精度越差，抵消效果越差。随着迭代次数的增加，可以检测到的有效径的信干比越来越小，其干扰抵消的效果收益也越来越小。本文提出的IPIC方法在迭代过程中性能优于SMUD迭代中的性能。由式(14)和式(16)，IPIC算法的第 i次迭代和干扰消除后残留干扰信号为

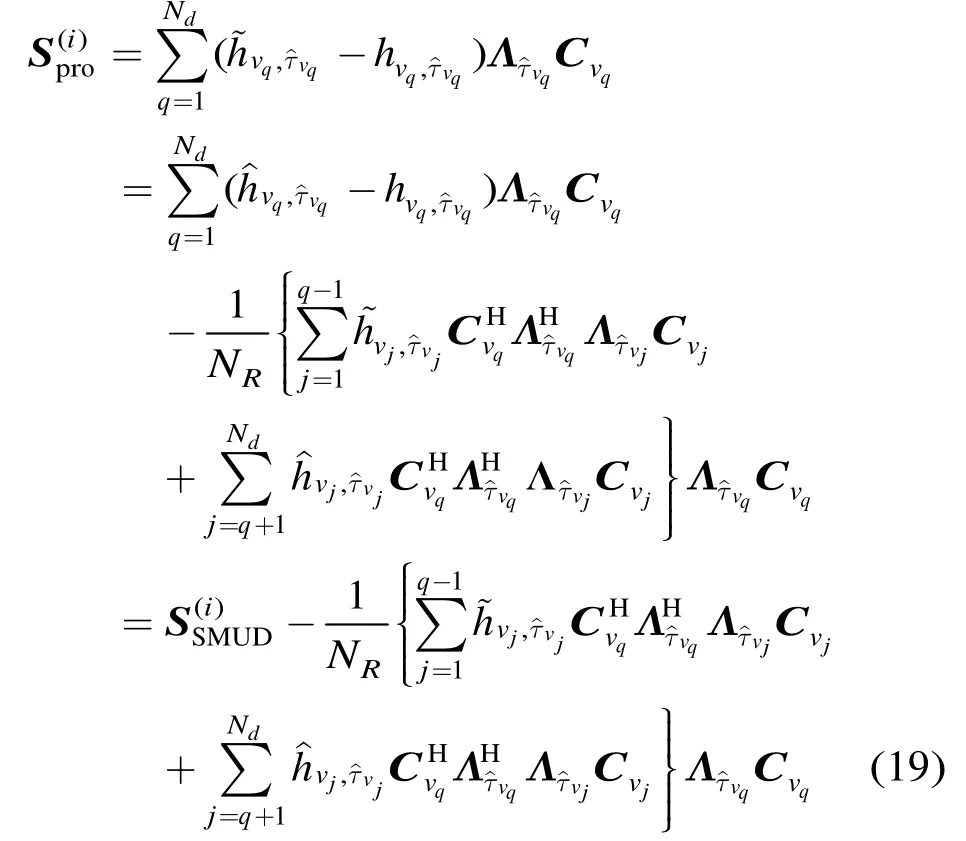
由式(20)可以看出，随着迭代次数增加，残留干扰信号将逐渐减少并趋于稳定，检测性能升高并趋于恒定；IPIC算法干扰消除后的残留信号与SMUD相比更少，因此能在较少的迭代次数下获得更好的检测性能。

4.3 复杂度分析

OFDMA上行链路有N个子载波，所提 IPIC算法和SMUD算法均利用N点IFFT变换完成频域相关运算。当存在RK 个测距用户同时接入时，SMUD算法需要次复数乘法及复数加法，而IPIC算法需要次复数乘法及复数加法。

5 仿真结果

为验证本文算法的有效性，在ITU规定的Vehicular Test A (VA)信道模型下，将IPIC算法与文献[12]中的SMUD算法对比。系统参数的选取遵循IEEE 802.16m标准[1]，OFDMA系统上行链路带宽为10 MHz，子载波个数为，采样率为11.2 MHz，载波频率为2.5 GHz, CP长度为个采样点。一个测距时隙由144个非连续子载波和2个OFMDA符号组成。假设小区半径，最大往返时延为个采样点，参考初始测距码个数为。在典型蜂窝移动环境下(速度小于120 km/h)，测距信号持续时间远小于信号相关时间，移动速度对于测距系统性能影响非常小，因此在仿真中考虑各测距用户的典型移动速度为60 km/h，多普勒频移为140 Hz。算法仿真中都用到了自适应门限，自适应门限保证虚警概率维持在左右。

图2给出了IPIC算法与SMUD算法在一个测距时隙内多用户接入的有效径信道系数估计的MSE对比曲线。可以看出，IPIC算法的有效径信道系数估计MSE比SMUD小，这表明IPIC算法的有效径信道系数估计更加接近于真实的有效径信道系数。当一个测距时隙内接入用户数(RSS)为8，且两者的有效径信道系数估计MSE精度相同时，IPIC算法所需信噪比与SMUD算法相比降低了约4 dB。

图3给出了IPIC算法与SMUD算法在一个测距时隙内多用户接入随信噪比的正确检测概率对比曲线。从图3可以看出，在一个测距时隙的活动用户数相同条件下，IPIC算法的检测概率大于SMUD，且随着信噪比增大，两者的检测概率均明显提升；在相同检测概率和相同信噪比条件下，IPIC算法所容纳的测距用户数大于SMUD。随着测距时隙内的活动用户增加，测距信道的MAI明显增大，导致两者检测概率均下降，但IPIC算法通过消除信道系数估计的有效径间互干扰，提高了有效径信道系数估计精度，能够更好地减小差错传播和残留MAI，因此正确检测概率仍高于SMUD。

图4给出了IPIC算法与SMUD算法在一个测距时隙内多用户接入所需复乘次数随信噪比的对比曲线。由图4可知，IPIC算法所需的复乘次数始终小于SMUD。当信噪比为9 dB，且一个测距时隙内接入用户数为6时，IPIC算法复杂度约为SMUD的25%，且能够获得比SMUD更好的检测性能。随着接入用户数的增加(＆gt;6)，SMUD算法的复杂度有所下降。这是由于测距信道的MAI增大，自适应门限有可能大于活动用户强功率径的相关峰值，导致迭代检测停止，同时也造成了检测性能下降。

图5给出了在信噪比为0 dB时，IPIC算法与SMUD算法在一个测距时隙内多用户检测性能随迭代次数的对比曲线。由图5可以看出，两种算法的正确检测性能均与迭代次数有关，当迭代次数较少时，正确检测性能较差，随迭代次数增加，正确检测概率提高并逐渐趋于恒定。在测距时隙中活动测距用户数和迭代次数相同的条件下，IPIC算法的正确检测性能优于SMUD。在测距时隙中活动测距用户数和检测概率保持稳定的条件下，IPIC算法所需的迭代次数远小于SMUD。在一个测距时隙中活动测距用户数为8，迭代次数等于5时，IPIC算法的检测概率达到0.74，而SMUD算法在迭代次数等于9时，其检测概率达到0.69。由于IPIC算法是并行迭代多用户检测，IPIC算法在获得较高的检测性能下所需要的迭代次数远小于SMUD，因此能够有效降低计算复杂度。

图2 IPIC算法与SMUD算法信道估计MSE对比

图3 IPIC算法与SMUD算法检测概率对比

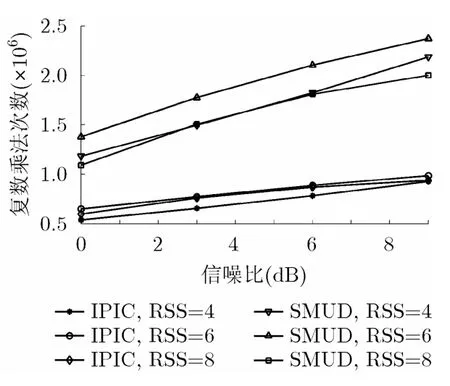
图4 IPIC算法与SMUD算法复杂度对比

图5 IPIC算法与SMUD算法检测概率随迭代次数对比

6 结论

针对 SMUD干扰消除初始测距算法性能不佳及复杂度过高的问题，本文提出了一种低复杂度迭代PIC的多用户初始测距算法。所提算法并行检测活动测距用户的时偏估计和初始信道系数估计，利用有效径参数估计部分消除信道估计干扰，通过重构和并行迭代消除多用户测距信号，有效提高了初始测距检测性能，降低了计算复杂度。本文提出的多用户初始测距算法在复杂度较低的情况下进一步改善了检测性能，便于工程实现，具有较强的工程实践价值，同时对其它OFDMA系统的多用户检测具有借鉴意义。

[1] IEEE Std 802.16m-2011. IEEE Standard for Local and Metropolitan Area Networks, Part 16: Air Interface for Broadband Wireless Access Systems Amendment 3:Advanced Air Interface[S]. 2011.

[2] Fu X and Minn H. Initial uplink synchronization and power control (ranging process) for OFDMA systems[C].Proceedings of the IEEE Global Telecommunications Conference, Dallas Texas, 2004: 3999-4003.

[3] Zhou Yue, Zhang Zhao-yang, and Zhou Xiang-wei. OFDMA initial ranging for IEEE 802.16e based on time-domain and frequency-domain approaches[C]. Proceedings of the IEEE International Conference on Communication Technology(ICCT), Guilin, 2006: 1-5.

[4] Mahmoud H, Arslan H, and Ozdemir M. An efficient initial ranging algorithm for WiMAX (802.16e) OFDMA[J].Computer Communication, 2009, 32(1): 159-168.

[5] Kim J Y, Kim J H, Kim H J, et al.. Performance analysis for simultaneous reception of initial ranging signal and data signal in wireless mesh networks[C]. Proceedings of the IEEE International Conference on Wireless Information Technology and Systems, Hawaii, 2012: 1-5.

[6] Lee K, Hwang W, and Choi H. An enhanced ranging algorithm for fixed wireless communication system[C].Proceedings of the 6th International Conference on Ubiquitous Information Management and Communication,Kuala Lumpur, 2012: 1-5.

[7] Fu X, Li Y, and Minn H. A new ranging method for OFDMA systems[J]. IEEE Transactions on Wireless Communications,2007, 6(2): 659-669.

[8] Morelli M, Sanguinetti L, and Poor H. A robust ranging scheme for OFDMA-based networks[J]. IEEE Transactions on Communications, 2009, 57(8): 2441-2452.

[9] Sanguinetti L, Morelli M, and Poor H. An ESPRIT-based approach for initial ranging in OFDMA systems[J]. IEEE Transactions on Communications, 2009, 57(11): 3225-3229.[10] Sanguinetti L, Morelli M, and Marchetti L. A random access algorithm for LTE systems[J]. Transactions on Emerging Telecommunications Technologies, 2013, 24(1): 49-58.

[11] 王薇, 杨维, 韩东升. IEEE802.16e系统上行链路初始测距算法研究[J]. 电子与信息学报, 2010, 32(4): 805-810.Wang Wei, Yang Wei, and Han Dong-sheng. Study on the initial ranging algorithm in uplink IEEE 802.16e system[J].Journal of Electronics ＆amp; Information Technology, 2010, 32(4):805-810.

[12] Ruan M, Reed M, and Shi Z. Successive multiuser detection and interference cancelation for contention based OFDMA ranging channel[J]. IEEE Transactions on Wireless Communications, 2010, 9(2): 481-487.

[13] Xia Yu-jie and Ren Guang-liang. Precoding-based initial ranging signal for SMUD algorithm in OFDMA systems[J].Electronics Letters, 2012, 48(18): 1167-1168.

[14] Lin C and Su S. A robust ranging detection with MAI cancellation for OFDMA systems[C]. Proceedings of the IEEE International Conference on Advanced Communication Technology (ICACT), Gangwon, 2011: 937-941.

[15] Sanguinetti L and Morelli M. An initial ranging scheme for the IEEE 802.16 OFDMA uplink[J]. IEEE Transactions on Wireless Communications, 2012, 11(9): 3204-3215.