Lai-Massey结构伪随机特性研究

郭 瑞金晨辉

(解放军信息工程大学 郑州 450004)

1 引言

1990年，Lai和Massey利用一类与Feistel模型，广义Feistel模型，SP网络以及其各种变型和组合等都不相同的模型设计了国际数据加密标准算法IDEA[1]。1999年，Vaudenay研究了IDEA算法采用的密码模型的一般化问题，提出了Lai-Massey结构[2]，其轮函数是，这里+表示某个群运算，双射σ是该群上的正形置换(即双射σ使仍是双射)或α几乎正形置换(使至多只有α个元素没有原象)。实现速度快是该结构的主要特点。2004年，文献[3,4]将Lai-Massey结构中的群运算具体为逐位模 2加，将双射变换σ具体为正形置换具体为SPS模型，设计了FOX系列分组密码算法(即 IDEA NXT)，从而给出了以 Lai-Massey结构为密码模型的一个分组密码实例。在对FOX算法的安全性分析方面，文献[5,6]构造了FOX算法的3轮积分区分器，并给出了迄今最优的积分分析的结果，证明了4轮FOX64/64, 5轮FOX64/128, 6轮FOX64/192, 7轮FOX64/256对碰撞-积分攻击不免疫；文献[7,8]先后给出了FOX算法的4轮不可能差分区分器，并给出了相应的不可能差分分析结果；文献[9]等则分析了FOX算法抗差错攻击的能力。此外，文献[10]给出了FOX算法的差分碰撞攻击。上述结果表明，在传统分析方法下，FOX系列算法展现了充分的安全性冗余。由此可得Lai-Massey结构是一类安全性较高的密码模型，值得进一步深入研究。

伪随机特性是设计密码模型需要满足的基本条件。在双射σ为正形置换的条件下，文献[2]和文献[11]使用不同的方法证明了Lai-Massey结构3轮复合可达伪随机条件，4轮复合可达超伪随机条件。针对不是任意群(如2mZ )上都存在正形置换的问题，文献[2]指出可以利用该群上的几乎正形置换设计双射σ，且证明了此时Lai-Massey结构的伪随机特性保持一致，从而推广了Lai-Massey结构的应用范围。然而，本文利用Lai-Massey结构的差分特性，证明了当双射σ为仿射几乎正形置换时，3轮Lai-Massey结构并不具有伪随机特性。

此外，2009年Luo等人[12]将Lai-Massey结构的群运算具体为异或运算，双射变换σ具体为线性正形置换，证明了Lai-Massey结构至少3轮复合达到伪随机性，至少4轮复合达到超伪随机性。但是，并未探讨Lai-Massey结构中不同正形置换和群运算对其伪随机特性的影响。因此，本文从Lai-Massey结构设计的角度出发，分析是否存在特定的群运算和正形置换使得Lai-Massey结构具有更好的伪随机特性。为此，本文利用构造区分器的方法证明了双射σ为任意正形置换时，3轮Lai-Massey结构具有伪随机特性的必要性；证明了双射σ为仿射正形置换时，3轮的Lai-Massey结构一定不具有超伪随机特性。结论表明，基于非线性双射σ设计的Lai-Massey结构可能具有更好的伪随机特性。

2 基础知识

本节首先给出伪随机置换和超伪随机置换的定义，然后介绍Lai-Massey结构及其伪随机特性。

2.1 伪随机和超伪随机置换

定义 1[2]令 :F为以密钥为索引的置换。如果对于任意概率多项式时间的攻击者 A，都存在一个可忽略函数，使得

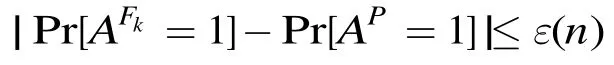
则称F是伪随机置换。其中密钥k在密钥空间中随机均匀选取，置换P从群G到G上构成的所有置换集合中随机选取。

定义 2[2]令 :F为以密钥为索引的置换。如果对于任意概率多项式时间的攻击者 A，都存在一个可忽略函数()nε，使得

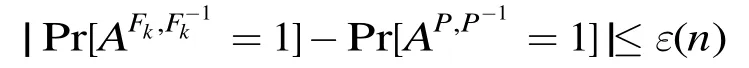
则称F是超伪随机置换。其中密钥k在密钥空间中随机均匀选取，置换P从群G到G上构成的所有置换集合中随机选取。

与定义1中的攻击者只具有选择明文的权利相比，定义2的攻击者A同时具有选择明文和选择密文的权利。

2.2 Lai-Massey结构及其伪随机特性[1317]-

定义 3[2]设kF和σ是群G到自身的映射且σ是双射，为交换群，k是圈密钥，则称以

为圈函数的分组密码为 Lai-Massey结构，并称kF是圈函数kQ的F函数，称σ是圈函数kQ的σ函数。

为保证Lai-Massey结构的加解密的相似性，最后一圈的圈函数一般设置为。

引理1[2]设σ是群G上的α几乎正形置换，如果攻击者A具有选择明文的权利，且询问预言机的能力限定为概率多项式时间，则有

引理2[2]设σ是群G上的α几乎正形置换，如果攻击者A同时具有选择明文和选择密文的权利，且询问预言机的能力限定为概率多项式时间，则有

3 双射σ为仿射几乎正形置换时，3轮Lai-Massey结构的区分器

特别地，在文献[17]中，给出了几乎正形置换的构造方法。

引理 3[17]设双射函数σ是群G上的置换。如果存在2λ≥，对于任意的LG∈，等式()xxL σ - =在群G上最多有λ个解，则此σ置换即为几乎正形置换，特别地，如果σ为仿射变换，则称σ为仿射几乎正形置换。

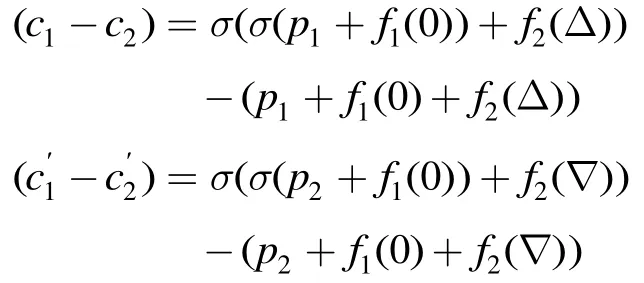
所以，当σ是仿射函数时，有

证毕

利用引理3给出的仿射几乎正形置换的构造方法，再结合引理5，则3轮Lai-Massey结构3LM 与随机置换P的区分器具体构造方法如下：

定理 1 设双射σ是群G上的仿射几乎正形置换。则攻击者A进行2次加密询问，可以的优势区分3轮Lai-Massey结构3LM 与随机置换P。

当攻击者A询问加密预言机O为3LM 时。由引理5可知区分算法输出为1的概率为1。

所以，该区分算法的区分优势为

证毕

文献[2]证明了基于几乎正形置换设计的 3轮Lai-Massey模型具有伪随机特性，而定理1说明当双射σ是群G上的仿射几乎正形置换时，3轮的Lai-Massey模型与随机置换是可区分的，从而给出一个反例。结论表明，基于仿射几乎正形置换设计的Lai-Massey模型并不具有特别好的伪随机性。即对于基于引理3构造的仿射几乎正形置换不适用于Lai-Massey模型的设计。因为存在使得，此时作为选择的消息，可以用于定理1中区分器的构造。

此外，Lai等人将Lai-Massey结构的群运算具体为异或运算，双射变换σ具体为线性正形置换，证明了Lai-Massey结构至少3轮复合达到伪随机性，至少4轮复合达到超伪随机性[11]。但是，并未探讨Lai-Massey结构中不同正形置换和群运算对其伪随机特性的影响。下面进一步研究基于一般的群运算和正形置换设计的 Lai-Massey结构的伪随机特性。

4 双射σ为正形置换时，2轮Lai-Massey结构不具有伪随机特性

引理6 对于2轮Lai-Massey结构(第2轮无σ变换)2LM ，选择两个不同的消息,进行加密，其中，则得到的输出必然满足等式，其中双射, 0表示加法群G中的单位元。

证毕

定理 2 设σ是群G上的任意正形置换。则攻击者A进行 2次加密询问，可以的优势区分2轮Lai-Massey结构2LM 与随机置换P。

证明 攻击者A具有询问加密预言机O的能力，其中O为2LM 或随机置换P，攻击者A构造可区分2轮Lai-Massey置换和均匀随机置换的算法如下：

所以，该区分算法的区分优势为

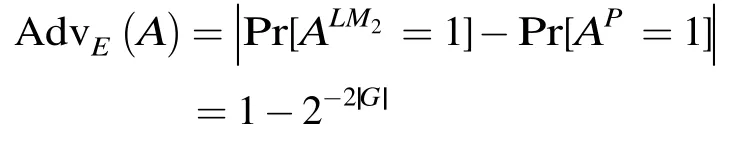
证毕

5 双射σ为仿射正形置换时，3轮 Lai-Massey结构不具有超伪随机特性

下面，利用同时进行选择明文和选择密文的方式，构造3轮Lai-Massey结构与随机置换的区分器。进而说明，当σ为仿射正形置换时，Lai-Massey结构至少4轮复合才具有超伪随机特性。

引理7 对于3轮Lai-Massey结构3LM ，设σ是群G上的仿射正形置换。选择两个不同的消息进行加密，其中，得到输出，再对进行解密，得到消息，其中要求2δ满足等式。则必有等式成立。其中由仿射正形置换决定的唯一常数。

进而得到等式：

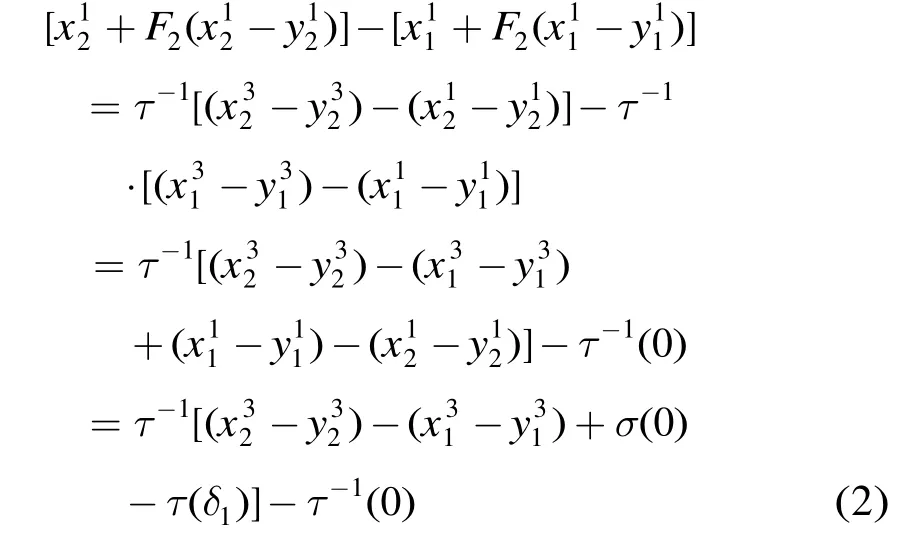
及等式：

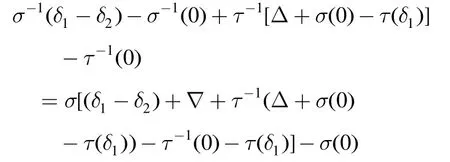
证毕

证毕

6 结束语

本文深入研究了 Lai-Massey结构的伪随机特性。首先，证明了基于仿射几乎正形置换设计的 3轮Lai-Massey模型并不具有伪随机特性，给出了设计者所得结论的一个反例。其次，证明了双射σ为任意正形置换时，至少3轮Lai-Massey结构才具有伪随机特性；证明了双射σ为仿射正形置换时，至少4轮的Lai-Massey结构才具有超伪随机特性。结论表明，构造伪随机特性更好的Lai-Massey结构实例，双射σ最好设计为非线性的正形置换或几乎正形置换。因此，分析是否存在非线性的正形置换σ使得3轮的Lai-Massey结构具有超伪随机特性，或者直接证明Lai-Massey结构是否至少4轮达到超伪随机特性，是值得进一步研究的问题。

[1] Lai X and Massey J. A proposal for a new block encryption standard[J]. LNCS, 1990, 473: 389-404.

[2] Vaudenay S. On the Lai-Massey scheme[J]. LNCS, 1999, 1716:8-19.

[3] Junod P and Vaudenay S. FOX: a new family of block ciphers[J]. LNCS, 2005, 3357: 114-129.

[4] Nakahara J. An analysis of FOX[J]. LNCS, 2009, 2010:236-249.

[5] Wu Wen-ling, Zhang Wen-tao, and Feng Deng-guo. Integral cryptanalysis of reduced FOX block cipher[J]. LNCS, 2005,3935: 229-241.

[6] 吴文玲, 卫宏儒. 低圈FOX分组密码的碰撞-积分攻击[J]. 电子学报, 2005, 33(7): 1307-1310.Wu Wen-ling and Wei Hong-ru. Collision-integral attack of reduced-round FOX[J]. Acta Electronica Sinica, 2005, 33(7):1307-1310.

[7] Wu Zhong-ming, Lai Xue-jia, Zhu Bo, et al.. Impossible differential cryptanalysis of FOX[J]. LNCS, 2010, 6163:236-249.

[8] 魏悦川, 孙兵, 李超. FOX密码的不可能差分分析[J]. 通信学报, 2010, 31(9): 24-29.Wei Yue-chuan, Sun Bing, and Li Chao. Impossible differential attacks on FOX[J]. Journal on Communications,2010, 31(9): 24-29.

[9] Li Rui-lin, You Jian-xiong, Sun Bing, et al.. Fault analysis study of the block cipher FOX64[J]. Multimedia Tools and Applications, 2013, 63(3): 691-708.

[10] Chen Jie, Hu Yu-pu, Zhang Yue-yu, et al.. Differential collision attack on reduced FOX block cipher[J]. China Communications, 2012, 9(7): 71-76.

[11] Yun Aaram, Park Je Hong, and Lee Jooyoung. On Lai-Massey and quasi-Feistel ciphers[J]. Design Codes Cryptography, 2011, 58: 45-72.

[12] Luo Yi-yuan, Lai Xue-jia, and Gong Zheng.Pseudorandomness analysis of the (extended) Lai-Massey scheme[J]. Information Processing Letters, 2010, 111(2):90-96.

[13] Yu Yu. Pseudorandom generators from regular one-way functions: new constructions with improved parameters[OL].http://eprint.iacr.org/2013/270. 2013.

[14] Alexandra Boldyreva and Virendra Kumar. A new pseudorandom generator from Collision-Resistant hash functions[J]. LNCS, 2012, 7178: 187-202.

[15] Andrej Bogdanov, Zeev Dvir, Elad Verbin, et al..Pseudorandomness for width-2 branching programs[J].Theory of Computing, 2013, (9): 283-293.

[16] Luca Trevisan. Pseudorandomness and derandomization[J].Association for Computing Machinery, 2012, 18(3): 27-31.[17] Jacques Patarin. How to construct pseudorandom and super pseudorandom permutations from one single pseudorandom function[J]. LNCS, 1992, 658: 256-266.