多源多中继协作网络上行联合波束成形

刘 琚 王 超 许宏吉 董 郑 Julian Cheng

（1.山东大学信息科学与工程学院，济南，250100；2.东南大学移动通信国家重点实验室，南京，211189；3.麦克马斯特大学电气与计算机工程学院，汉密尔顿，加拿大，L8S4K1；4.英属哥伦比亚大学工程学院，基隆拿，加拿大，V1V1V7）

引 言

由于能够提高无线通信系统的频谱效率和可靠性［1］，天线分集技术在近几十年得到了广泛的关注。这种优势通常被称作多路复用和分集增益［2］。在所有可以实现空间分集增益的方案中，波束形成技术由于其收发端可以形成多个波束因而最受关注［3－4］。

在一个实际的蜂窝网络中，在基站端装配多天线是十分常见的，然而对于移动设备而言，由于受到体积和电池寿命的限制，装配多天线并不可行。协作波束形成技术可以有效的解决上述问题，不同的移动用户共享彼此的天线，通过分布式信号处理和协作通信技术，这些天线就形成了虚拟的天线阵列，研究证明可以有效地替代多天线系统［5－11］。如果在发送端、中继节点和接收端之间的瞬时信道状态信息不能直接获取，最优化的波束形成可以通过分散技术解决［8－9］。如果仅仅是二阶信道状态信息已知，对于每一个中继节点都存在功率约束的情况，其最优化的波束形成设计问题可以通过对优化向量进行半正定松弛，进而转化成半正定规划问题求解［10］。上述优化问题可以扩展到多源多宿的情形［11］。

不同于文献［7－11］中那样所有的节点都是装配着单天线，本文将研究基站端配置有多天线的情形［12］。在这种情形中，用户可以通过分布式的中继节点独立的向配置有多天线的基站端发送信号，这是出于目的节点作为上行链路中的基站端的考虑。这个网络模型与文献［5］具有根本的不同，为减少信号传输的开销，分布式的用户之间以及中继节点之间的通信不被允许。此外，本文模型也不同于文献［11］，用户之间遭受严重的信号干扰。在本文的研究中，不同用户之间的干扰可以被多天线基站有效地估计。在文献［12，13］中的优化问题采用了迭代的方法解决，这种方法容易陷入局部最优。在文献［14］中采用了遗传算法，但是由于遗传算法属于一种启发式搜索的方法，计算复杂度高，难以满足实时性的要求。

本文假设基站端的线性接收器没有反馈从而减少系统的复杂度。为了取得更好的波束形成效果，提出了两种相关但是又不相同的波束形成设计方法：总功率最小化方法（在每个用户对应的信干噪比满足一定约束的前提下使中继节点总功率消耗最小化）、信干噪比最大化方法（在中继节点满足一定功率约束的前提下使最小的信干噪比最大化）。上述方法所面对的都是包含有中继节点波束形成加权向量和基站端线性均衡向量的多变量联合优化问题，直接处理起来非常困难。为了得到最优化的解，通过一定的数学转换将线性均衡向量表示成中继加权向量闭式解的形式，上述多变量问题转化成仅包含中继加权向量的问题。进而两种方法都可以运用内点法有效地求得最优化的解，并且避免了迭代运用凸优化的弊端。

1 系统模型

考虑如图1所示的多源多中继协作网络，K个单天线用户通过M个单天线中继节点采用放大转发策略实现与包含N根天线的基站之间的通信。其中第k个源节点的发送功率为pk，所有噪声都为平稳高斯白噪声，在中继节点处噪声功率为，在基站处噪声功率为。用户与基站之间的通信可以分为两个阶段。在第1个阶段所有的源节点同时向中继节点广播信号，在第m个中继节点的接收信号为

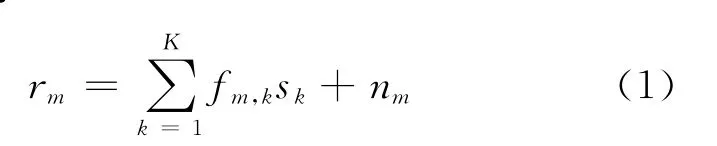
式中：fm，k∈C表示从第k个源节点与第m个中继节点之间的信道参数。每一个源节点都用最大允许功率Pk发送信号，并且sk表示第k个源节点发送的信号符号（k＝1，2，…，K）。nm表示第m个中继节点处的复高斯噪声。式（1）可以改写成向量的形式

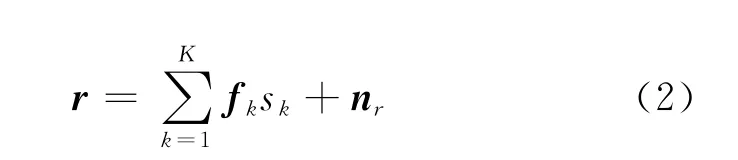
式中：r＝ ［r1，r2，…，rM］T，fk＝ ［f1，k，f2，k，…，fM，k］T，nr＝［n1，n2，…，nM］T。在第二个阶段，通过乘上波束形成加权系数wm，第m个中继节点将接收到的信号放大转发。转发信号可以表示成t＝WHr，其中进而中继节点的总传输功率可以表示成

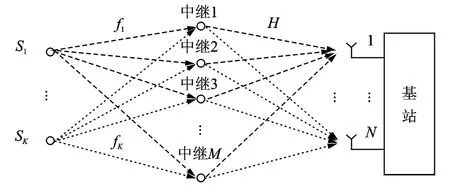
图1 系统模型Fig.1 System model

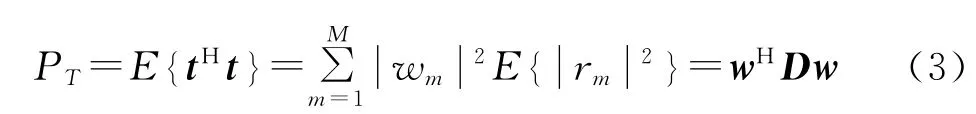
式中：D是对角阵，其第m个对角线元素为

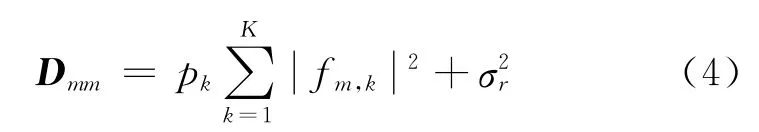
从中继节点到多天线基站之间的信道矩阵为H∈CN×M，则可将基站端的接收信号表示成

式中：nd表示目的节点处的噪声。针对实际情况，在基站端的多天线采用线性均衡。设均衡矩阵为

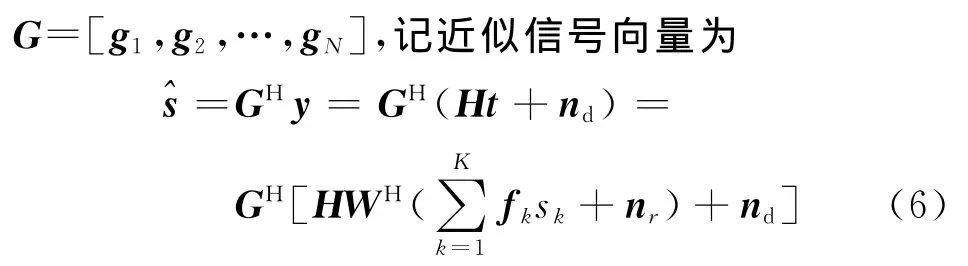
则第k个源节点所对应的基站接收信号可以表示为

2 基站端最优化线性均衡设计

假设基站可以收集信道状态信息（Channel state information，CSI），获得优化波束形成向量。根据式（7）可得第k个源节点所对应的基站端接收信号功率为

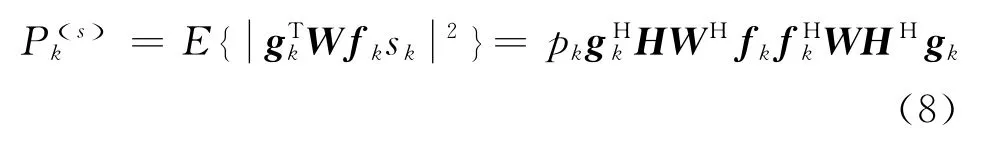
所对应的干扰信号功率为

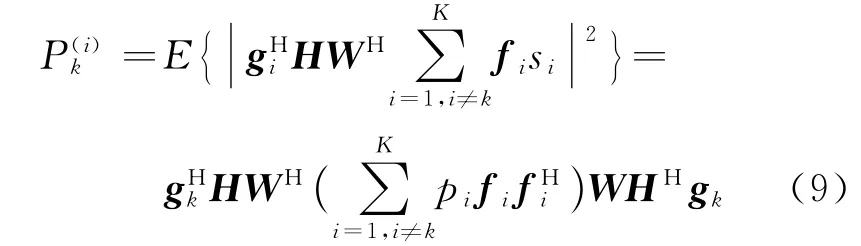
所对应的噪声信号功率为

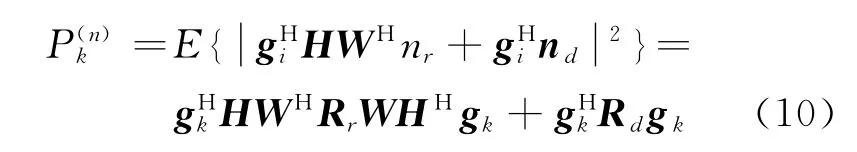
因此第k个源节点所对应基站端接收信号的信干噪比为

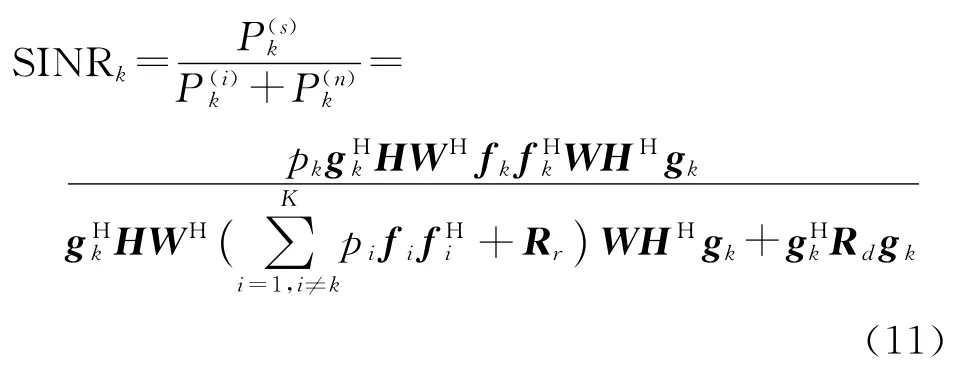
可以进一步改写成

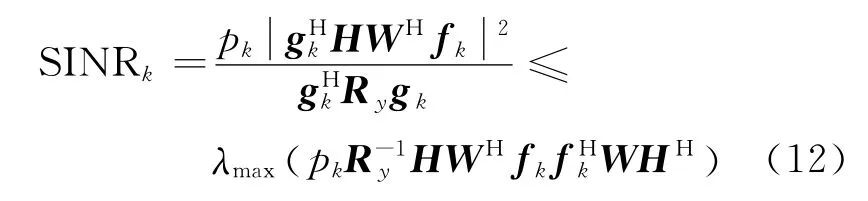
式中：λmax（B）表示矩阵B的最大特征值，并且Ry＝式（12）来自Cauchy－Swartz不等式。通过设定可以取得等号成立。

3 总功率最小化方法

考虑在目的节点SINRk不小于阈值γk＞0（1，2，…，K）的前提下，使中继节点总传输功率最小化。可以用如下表达式表示

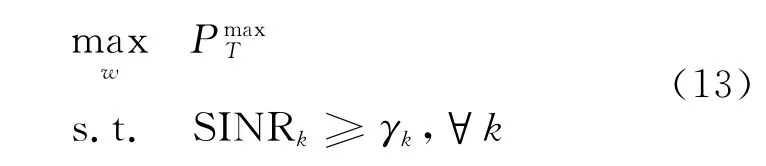
令Bk＝（HWHQkWHH＋Rd）－1当设置gk∝时，优化问题式（13）可以改写成

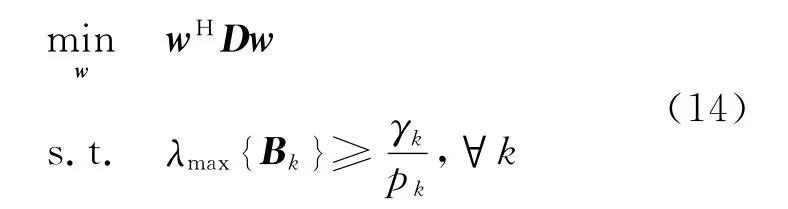
由于Bk是半正定矩阵，并且∀k，每一个Bk都有唯一的非零特征值，当然也是最大特征值

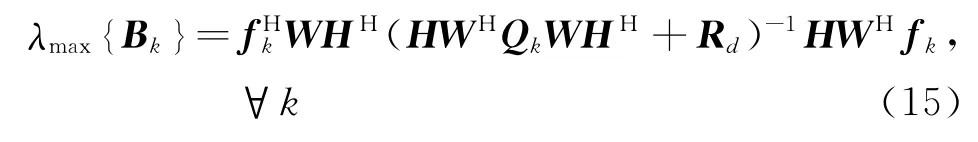
因此，优化问题式（14）等效于

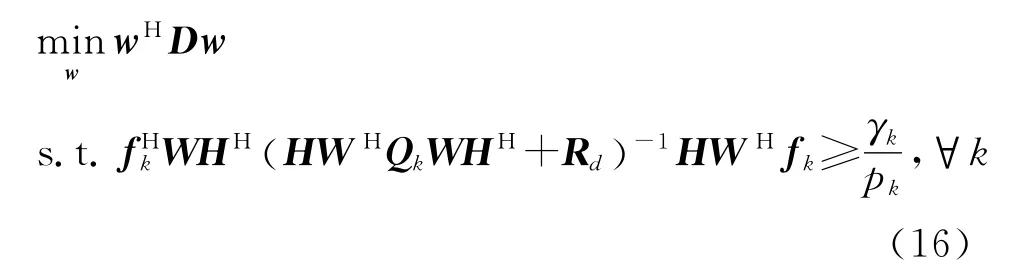
根据Duncan－Guttman矩阵逆式［15］，优化问题可以进一步改写成

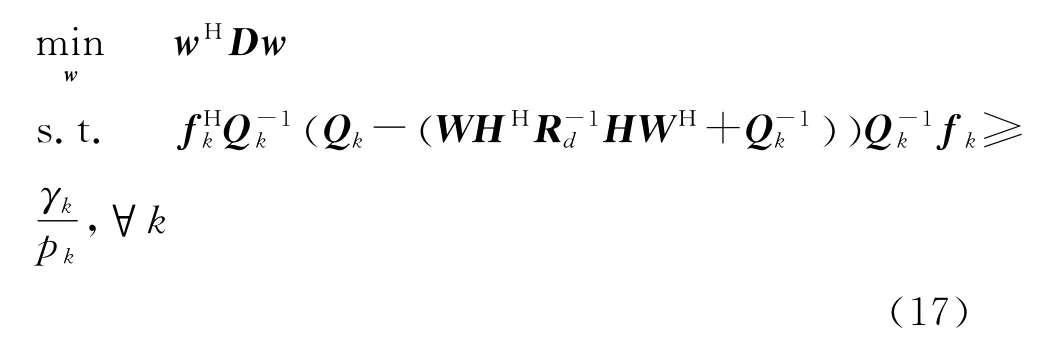
上式可以进一步改写成Schur补的形式

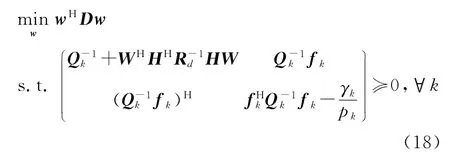
一般而言，上述优化问题不容易直接解决，但通过定义X≜wwH，此 时进而原优化问题可以转化为

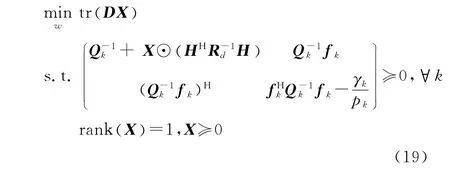
式中的rank（X）＝1约束是非凸的并且会带来难以承受的计算复杂度。果断地松弛该约束（从仿真中也很少遇到不满足秩约束的情形），上式转化成一个半正定规划问题，进而可以运用凸优化工具包比如凸优化工具包（Convex optimization toolbox，CVX）［16］十分迅速地解决［17］。如果X的秩为1，那么对应的优化向量w就是最优化的波束成形权向量。反之如果在极少数的情况下秩不为1，则可以运用一种随机化技术来确定秩为1的最优解。在最优的协作波束形成权值向量wopt确定之后，最优化的基站端线性均衡向量可以用gk＝ρ∀k确定，这里ρ｛B｝表示矩阵B的归一化主特征向量。

4 信干噪比最大化方法

本文力求在中继节点总功率满足不大于的前提下使得最小的最大化，数学上可以表示成如下这种max－min－fair的形式

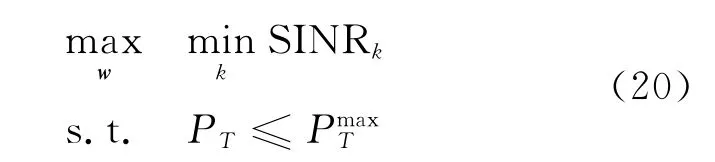
通过引入中间变量t，可以将式（23）转化成

利用Schur补，式（21）转化为

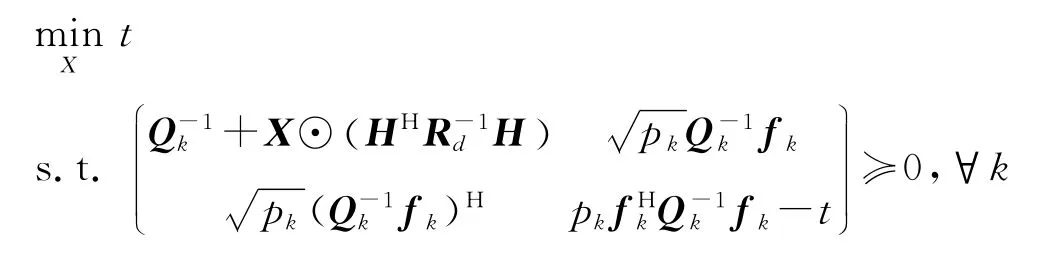
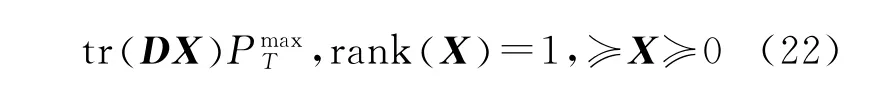
式（22）是一个双线性矩阵不等式约束下的优化问题，可以利用二分法有效地解决。首先假定问题可行，从一个已知的含有最优值tmax的区间［l，u］开始，在区间中点处解凸可行性问题，来确定最优值是大于t还是小于t。如果t可行，设l＝t，如果不可行则使u＝t，更新区间直到u－l＜ε，ε是最大允许偏差。将t代回式（22），通过半正定松弛，形成线性不等式的约束，式（22）进而可以用CVX解决。若秩不为1，则可用随机化技术式［18］得到秩为1的解。最优化的中继节点加权向量确定后，最优的线性均衡矩阵也可以有效地获得。

5 仿真结果分析

采用与文献［12］相同的信道模型。同样假设信道参数和信道状态信息在基站端可以获取，并且信道参数之间相互独立，源节点的发送信号功率设定为比噪声功率高10dB，并且信道估计错误为10 dB，信道增益设置为0dB。

图2是第3节总功率最小化方法的结果，其中仿真了不同的K，M，N值所对应的最小化的中继传输总功率。不失一般性，SINRk设置成高于相同的门限值γk＝Γ，∀k。从图中可以看出，随着中继节点和接收天线数的增加而减少，这是由于在复散射环境中，随着天线数目的增加，寻找更好天线路径的机会增加了。从图中还可以看出与文献［12］中的方法相比，本文方法可以降低大约1dBW的功率消耗，在高信噪比区域功率降低的幅度更为明显。这是因为方法能够实现全局最优，避免了式［12］中的迭代过程。

图3是第4节信干噪比最大化方法的结果，仿真了中继总功率约束下最大化可实现的最小的信干噪比最大化 S－SINRs（the smallest of SINRk，∀k）。从图中可以看出，最大化可实现的S－SINRs随着中继节点数目的增加而增加，并且随着最大允许的中继节点总功率的增加而增加，并趋于饱和。并且该方法远好于固定功率方法，最大化可实现的S－SINRs有3～5dB的提高。

6 结束语

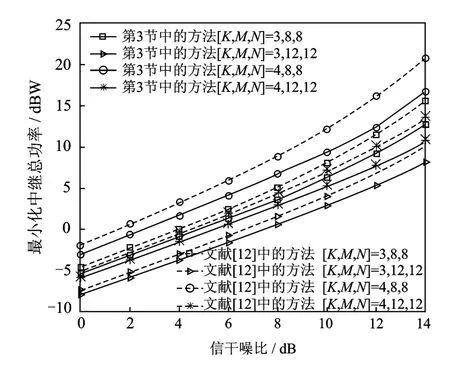
图2 总功率最小化方法Fig.2 Total power minization method

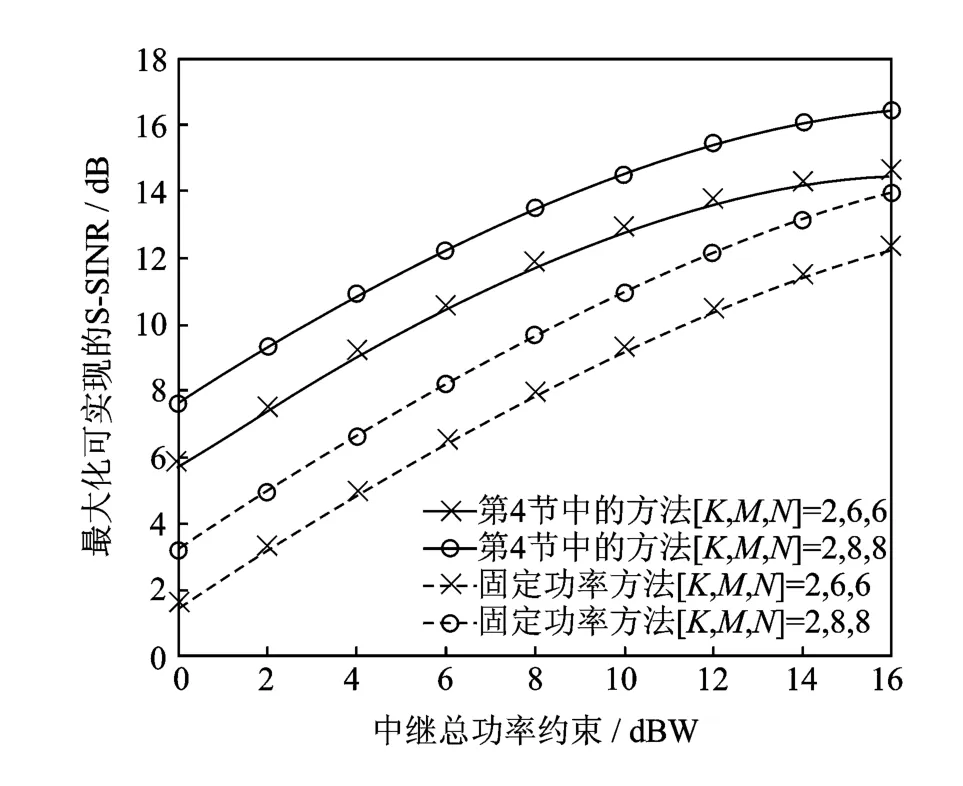
图3 信干噪比最大化方法Fig.3 SINR maximization method

针对多源多中继的基站端配置有多天线的协作通信网络，提出了两种中继加权向量和基站端线性均衡向量的联合优化方法。上述优化问题包括两个待优化变量，直接解决起来非常困难，通过数学转化，将基站端线性均衡向量用中继加权向量闭式表示，进而将多变量的优化问题转化成只包含中继加权向量的优化问题。随后通过运用Schur补和半正定松弛将上述问题转换为凸问题用内点法可以非常有效地求得最优解。仿真结果表明，本文所提出的方法远好于现有的方法，可以获得更高的服务质量或者相同情形下降低中继传输功率，并且避免了式［12］中的迭代过程，降低了计算复杂度。

［1］Telatar I E，Capacity of multi－antenna gaussian channels［J］.Europ Trans Telecommun，1999，10：585－595.

［2］Zheng L，Tse D N C.Diversity and multiplexing：A fundamental tradeoff in multiple－antennas channels［J］.IEEE Trans Inf Theory，2003，49：1073－1096.

［3］张艳.基于非规则LDPC码的协作MIMO系统性能分析［J］.数据采集与处理，2013，28（6）：714－718.Zhang Yan.Based on irregular LDPC Cooperative MIMO system performance analysis［J］.Journal of Data Acquisition and Porcessing，2013，28（6）：714－718.

［4］于斌，胡捍英.单小区功率约束下的多小区协同波束成形［J］.数据采集与处理，2013，28（1）：87－91.Yu Bin，Hu Hanying.Coordinated beamforming for the multi－Cell systems with per－Cell power constraints［J］.Journal of Data Acquisition and Processing，2013，28（6）：87－91.

［5］Palomar D P，Cioffi J M，Lagunas M A.Joint Tx－Rx beamform－ing design for multicarrier MIMO channels：A unified framework for convex optimization［J］.IEEE Trans Sig Proc，2003，51：2381－2401.

［6］Laneman J，Tse D N C，Wornell G W.Cooperative diversity in wireless networks efficient protocols and outage behaviour［J］.IEEE Trans Inf Theory，2004，5：3062－3080.

［7］Jing Y，Hassibi B.Distributed space－time coding in wireless relay networks［J］.IEEE Trans Wireless Commun，2006，55：3524－3536.

［8］Jing Y，Jafarkhani H.Network beamforming using relays with perfect channel information［J］.IEEE Trans Inf Theory，2009，55：2499－2517.

［9］Zheng G，Wong K K，Paulraj A，et al.Collaborative－relay beamforming with perfect CSI：optimum and distributed implementation［J］.IEEE Sig Proc Letters，2009，16：257－260.

［10］Nassab V，Shahbazpanahi S，Grami A，et al.Distributed beamforming for relay networks based on second－order statistics of the channel state information［J］.IEEE Trans Sig Proc，2008，56：4306－4316.

［11］Dehkordy S F，Shahbazpanahi S，Gazor S S.Multiple peer－to－peer communications using a network of relays［J］.IEEE Trans Sig Proc，2009，57：3053－3062.

［12］Zheng Y，Blostein S.Optimization of power constrained multi－source uplink relay networks［C］／／Proc IEEE Globecom.Honolulu，Hawaii，USA：IEEE，2009：1－6.

［13］Khandaker M R A，Rong Y.Interference MIMO re－lay channel：Joint power control and transceiver－relay beamforming［J］.IEEE Trans Sig Proc，2012，60：6509－6518.

［14］Wang C，Liu J，Xu H，et al.Joint receiver－and－collaborative beamforming for the multi－user relay network in the uplink［C］／／Proc IEEE WCSP.Huangshan，Anhui，China：IEEE，2012：1－5.

［15］Piegorsch W，Casella G E.Inverting a sum of matrices［J］.SIAM Review，1990，32：470.

［16］CVX Research，Inc.CVX：Matlab software for disciplined convex programming［EB／OL］.version 2.0 beta.http：／／cvxr.com／cvx，2012.

［17］Grant M，Boyd S.Graph implementations for nonsmooth convex programs，in recent advances in learn－ing and control［EB／OL］.http：／／stanford.edu／boyd／graph－dcp.html.2008.

［18］Luo Z Q，Ma W K，So A M C，et al.Semidefinite relaxation of quadratic optimization problems［J］.IEEE Sig Proc Mag，2010，27：20－34.