MIMO阵列中基于PM和降维变换的高效DOA估计算法
2014-11-17张小飞张立岑陈未央徐大专
张小飞 张立岑 陈未央 徐大专
(南京航空航天大学电子信息工程学院,南京,210016)
引 言
多输入多输出 (Multiple-input multiple-output,MIMO)阵列利用多根天线同时发射信号来探测目标,并同时用多根天线接收相应的目标反射信号[1-5],已被广泛应用于雷达和通信系统。相比单根天线的传输系统,MIMO阵列系统拥有更多自由度,这些额外的自由度能使之克服衰落效应,增强参数的可识别性并提高目标探测性能[5-9]。目前,已经有很多关于MIMO阵列的角度估计算法[10-21]。包括最大似然方法[10],Capon算法[11-13],多重信号分类(Multiple signal classification,MUSIC)算法[14-16],求根 MUSIC 算法[17],借 助旋转不变性估计信号参数(Estimation of signal parameters via rotational invariance techniques,ES-PRIT)算法[18-19],平行因子(Parallel factor,PARAFAC)方法[20]以及自适应PARAFAC算法等[21-22]。然而,最大似然算法需要全局极值的多维搜索,这会导致更高的计算复杂度;Capon算法和MUSIC算法需要高复杂度的谱峰搜索;ESPRIT算法和求根MUSIC算法需要对互相关矩阵进行特征值分解来获得信号子空间或噪声子空间;PARAFAC算法和自适应PARAFAC算法是迭代算法,这通常比子空间算法需要更高的复杂度。
传播算子方法(Propagator method,PM)是一种低复杂度的算法[22-24],它无需谱峰搜索,也无需对互相关矩阵进行特征值分解,也无需对接收数据进行奇异值分解。本文提出了一种MIMO阵列下基于PM算法和降维变换的低复杂度的波达方向(Direction of arrival,DOA)估计算法。该算法在无需谱峰搜索的情况下获得了较好的估计性能。相比于传统的PM算法,本文提出的算法复杂度更低,并且估计性能更好。此外,本文推导了该算法的估计误差以及克拉美罗界。仿真实验说明了该算法在各种情况下的准确性和有效性,特别是当目标间隔很近的时候。
1 数据模型
考虑一个包含M个发射天线和N个接收天线的单基地MIMO阵列系统,并且发射和接收阵列都是均匀线阵,天线间隔均为半波长。假设有K个不相关的目标,接收端匹配滤波器的输出可以表示为
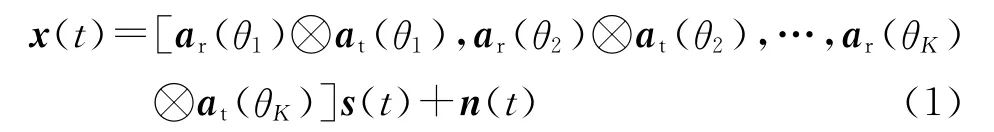
式中:θk是第k个目标的到达角;s(t)=[s1(t),s2(t),…,sK(t)]T∈CK×1且sk(t)=βkej2πfkt,fk是多普勒频率,βk是幅度;ar(θk)和at(θk)分别是第k个目标的接收方向矢量和发射方向矢量;ar(θk)⊗at(θk)是它们的 Kronecker积;n(t)是一个零均值协方差矩阵为σ2IMN的MN×1高斯白噪声向量。定义A=[ar(θ1)⊗at(θ1),ar(θ2)⊗at(θ2),…,ar(θK)⊗at(θK)]。进行L次采样,同时定义X=[x(1),x(2),…,x(L)],可表示为
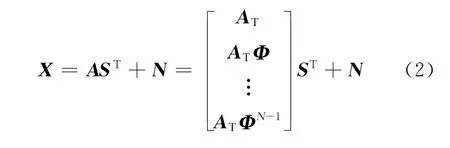
式中:AT=[at(θ1),at(θ2),…,at(θK)]∈CM×K是发射方向矩阵;N∈CMN×L是噪声矩阵;S=[s(1),s(2),…,s(L)]T∈CL×K,Φ=diag(exp(-jπsinθ1),exp(-jπsinθ2),…,exp(-jπsinθK))。
2 MIMO阵列中的DOA估计
2.1 MIMO阵列中的PM估计算法
对矩阵AT分块如下
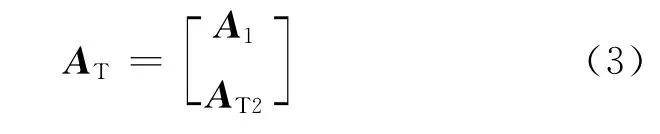
式中:A1∈CK×K;AT2∈C(M-K)×K。A1是满秩矩阵。矩阵A可以表示为

式中:A1∈CK×K,A2∈C(MN-K)×K。A2可以表示为写为A1的线性变换,写为A2=PcA1,其中Pc是传播算子矩阵。对矩阵Pc分块如下
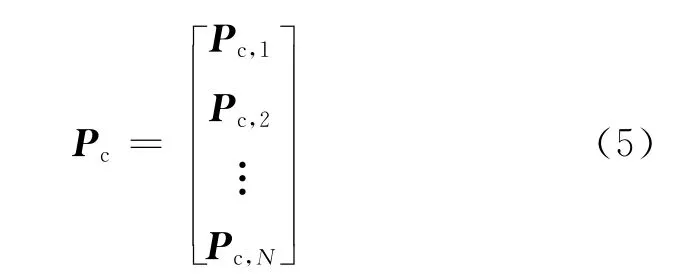
式中:Pc,1∈C(M-K)×K,Pc,n∈CM×K,n=2,…,N。矩阵A2也可以如上所述进行分块,可以得到
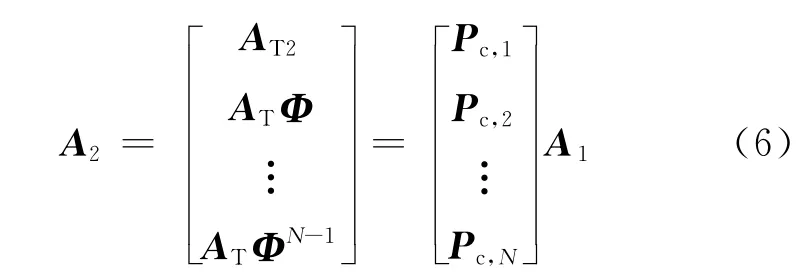
根据式 (6)
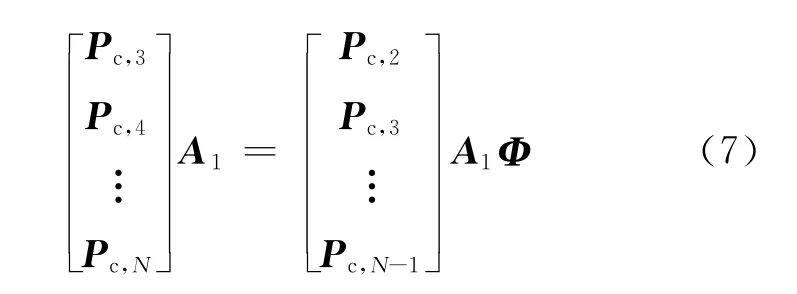
对矩阵X分块得到,其中X1∈CK×L,X2∈C(MN-K)×L。通过式(8)可以得到矩阵Pc的估计

将MIMO阵列下的PM估计算法的主要步骤总结如下
(1)由接收信号对传播算子Pc估计,用表示。
(2)构建和。
(3)对Ψc进行特征值分解来估计Φ,其中最终对DOA进行估计。
PM算法可以用于MIMO阵列的DOA估计,并且它的复杂度可以被进一步减少。在接下来的部分,提出了MIMO阵列下一种基于PM和降维变换的低复杂度DOA估计算法,该算法比PM算法复杂度更低。
2.2 MIMO阵列中的降维PM估计算法
ar(θk)⊗at(θk)可以用下式表示
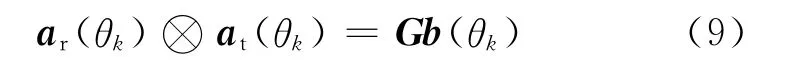
式中:b(θk)=[1,exp(-jπsinθk),…,exp(-jπ(M+N-2)sinθk)]T,M,N分别为发射天线数和接收天线数,并且矩阵G为
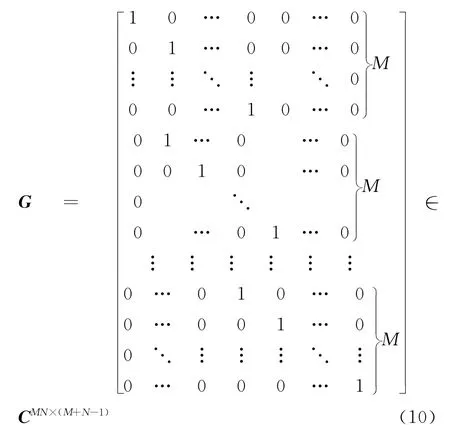
根据式(10),定义W≜GHG,如式(11)所示
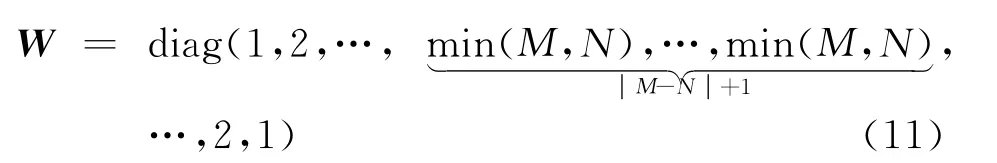
对接收信号x(t)使用降维变换W-1GH,得到
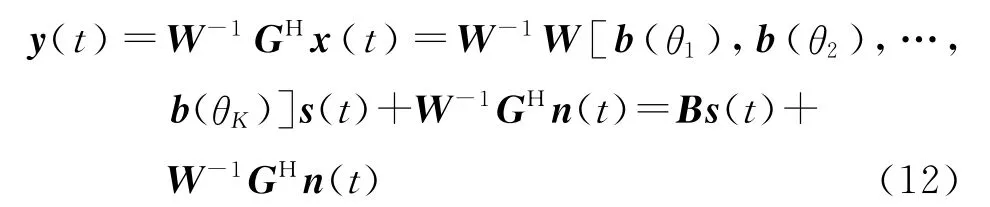
式中:B=[b(θ1),b(θ2),…,b(θK)]∈C(M+N-1)×K是范德蒙矩阵。由于降维变换矩阵是稀疏的,它的转换仅增加了很小的计算量。矩阵B可以被表示为

式中:B1∈CK×K,B2∈C(M+N-1-K)×K。B1是满秩矩阵。定义B2=PB1,其中矩阵P是传播算子。式(13)中的矩阵B2可以被重新写为
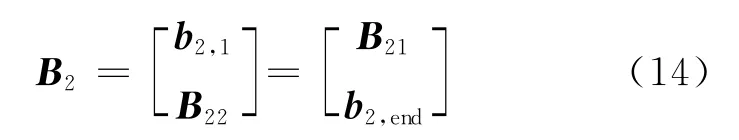
式中:b2,1∈C1×K和b2,end∈C1×K分别是B2的第一行和最后一行。B22=B21Φ,其中Φ=diag(exp(-jπsinθ1),exp(-jπsinθ2),…,exp(-jπsinθK))。传播算子矩阵可由式(15)表示
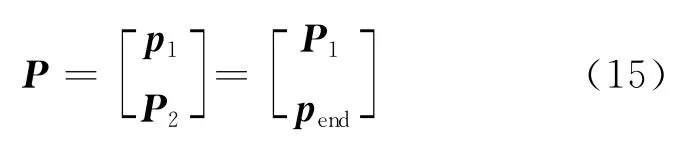
式中:p1∈C1×K和pend∈C1×K分别是P的第一行和最后一行。根据式(14,15),有

根据式(16),P2=P1B1,那么2=B1。定义Ψ≜2,因为Ψ和Φ有相同的特征值,通过对Ψ进行特征值分解来得到Φ,进而获得DOA估计。
对降维信号进行L次采样并定义Y=[y(1),y(2),…,y(L)],它可由表示,其中Y1∈CK×L,Y2∈C(M+N-1-K)×L。进而可以得到P的最小二乘估计

到目前为止,已经完成了单基地MIMO阵列下基于PM和降维变换的DOA估计算法。将该算法的主要步骤总结如下:
(1)对接收信号进行降维变换:
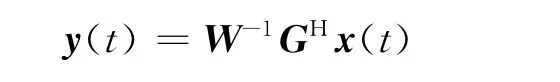
(2)由y(t)对传播算子P进行估计,用表示。
(3)构建和。
(4)对Ψ进行特征值分解来估计Φ,其中Ψ=,并最终对DOA进行估计。
2.3 复杂度分析和算法优点
与传统PM相比,本文所提出算法具有低复杂度。令L,K分别为快拍数和目标数,则本文所提出算法的复杂度为O(LK2+5K3+(M+N-1-K)K2+2(M+N-2-K)K2),而PM 和ESPRIT算法复杂度分别为O(LK2+5K3+(MN-K)K2+2(MN-2M)K2),O(M2N2L+M3N3+2M(N-1)K2+3K3)。图1给出了M=8,N=8,K=3情况下下的复杂度对比,从图1可以看出本文所提出算法复杂度低于传统PM算法,并远低于ES-PRIT算法。
本文提出算法具有如下优点:
(1)所提出算法的复杂度低于PM;
(2)所提出算法的角度估计性能略好于PM。
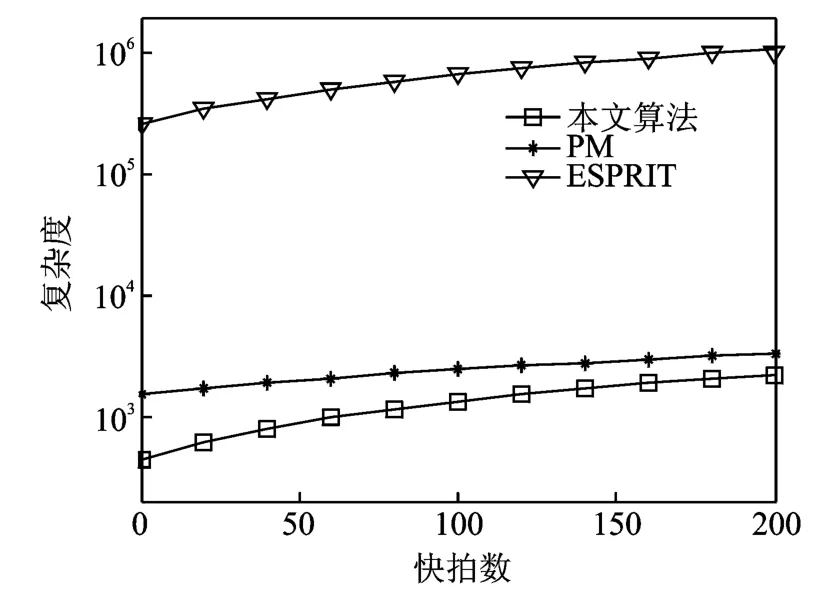
图1 复杂度对比Fig.1 Complexity comparison
3 性能分析
假设=P+∂P,其中∂P为误差估计矩阵。则根据式(14,15),有
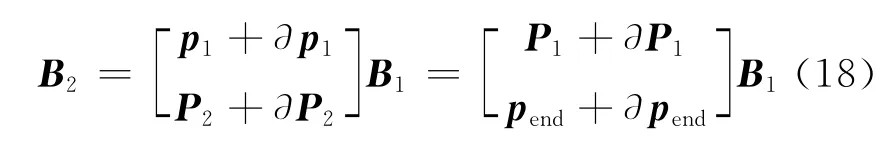
式中:∂p1和∂pend分别为∂P的第一行和最后一行。根据[P1+∂P1]+的一阶近似,得到
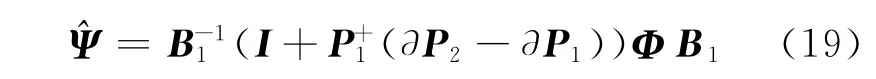
的第k个特征值为是=λk+∂λk,其中为单位矢量,且该矢量中第k元素为1,其他为0。进而可推导出DOA估计误差方差为
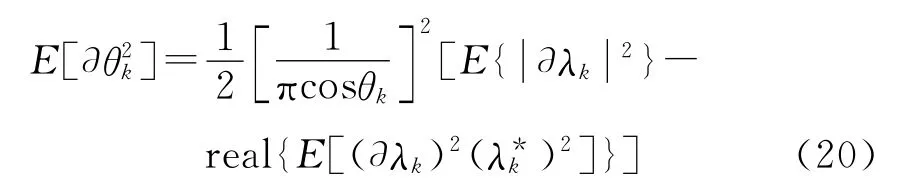
式中E[·]为期望。
根据文献[25],推导出 MIMO阵列DOA估计的克拉美罗界(Cramér-rao bound,CRB)为
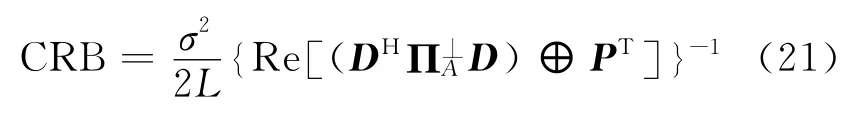
4 仿真结果
通过Monte Carlo仿真来评价本文提出的算法的角度估计性能。定义均方根误差为其中是第n次Monte Carlo试验的到达角θk的估计值。
图2~6的仿真中采用3个分别位于θ1=10°,θ2=20°和θ3=30°的非相关目标的 MIMO阵列系统。
图2给出了提出的算法在M=8,N=8,L=100和SNR=10dB时对所有3个目标的角度估计结果,从图中可以看出DOA可以被清楚地分辨。
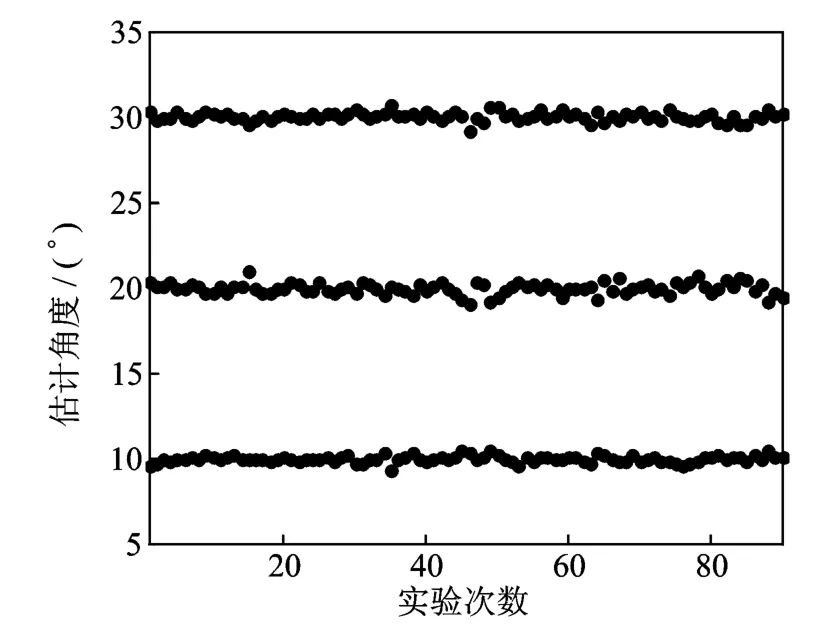
图2 SNR=10dB情况下的角度估计性能Fig.2 Angle estimation results with 10dB
图3给出了在M=8,N=8,L=100时不同算法的DOA估计性能对比,包括本文提出的算法,PM算法,以及CRB。图3表明该算法比PM算法拥有更好的角度估计性能。
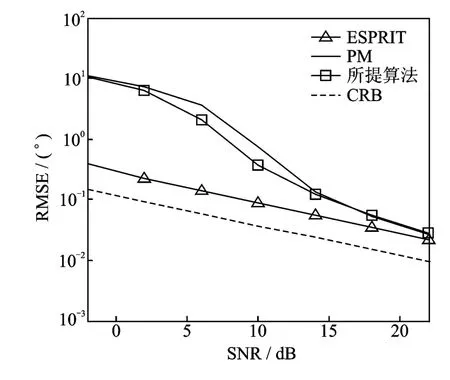
图3 角度估计性能对比Fig.3 Angle estimation comparison
图4给出了提出的算法在M=8,N=8,且L取不同值时的角度估计性能。图4表明算法的角度估计性能随L的增加而提高。
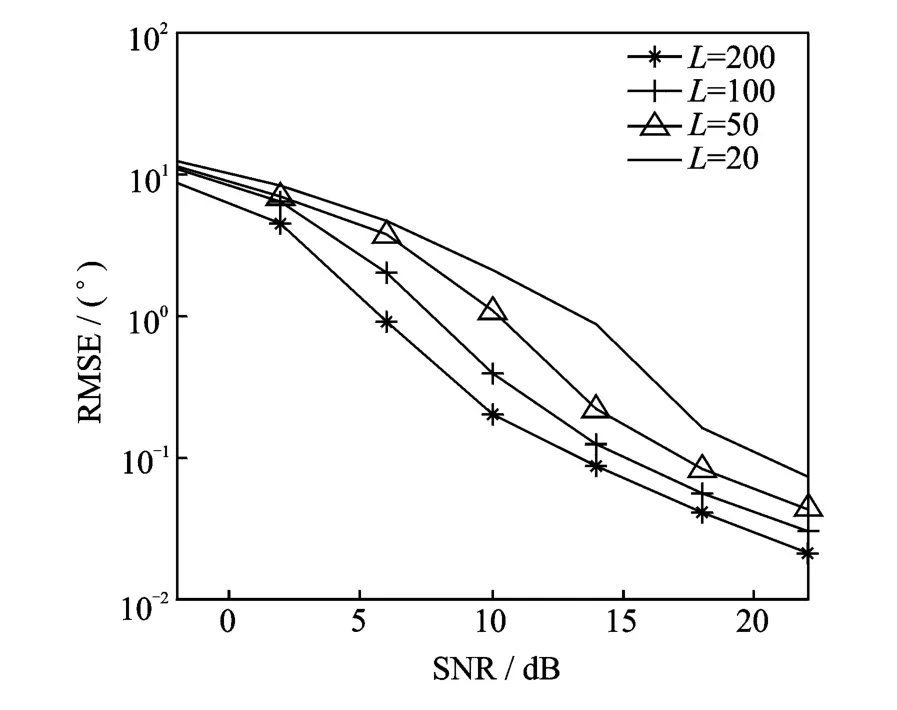
图4 不同L情况下角度估计性能Fig.4 Angle estimation with different values of L
图5,6给出了在L=100,K=3且M/N取不同值的情况下该算法的角度估计性能。从图5,6可知,算法的角度估计性能随接收和发射天线数量的增加而提高。由于分集增益特性,更多的接收或发射天线提高了算法的角度估计性能。
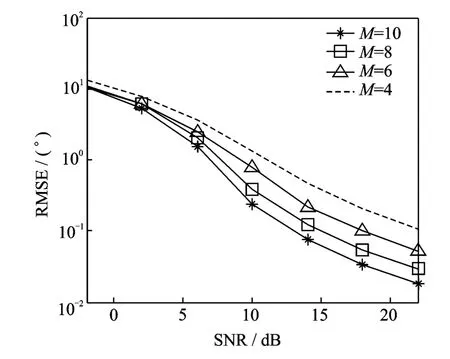
图5 不同M情况下角度估计性能(N=8)Fig.5 Angle estimation with N=8and different values ofM
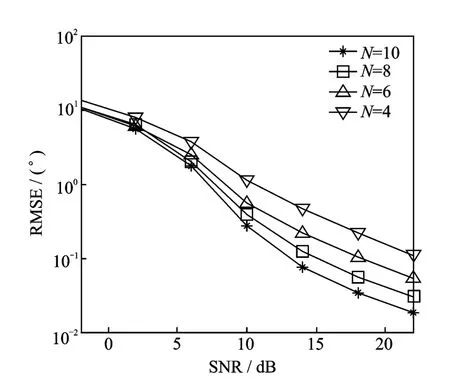
图6 不同N情况下角度估计性能(M=8)Fig.6 Angle estimation with M=8and different values of N
图7给出了在M=8,N=8,L=100时,两个间隔很近的目标情况下该算法的角度估计性能。这两个紧密间隔的目标分别位于θ1=10°和θ2=13°。从图7中发现在目标紧密间隔时该算法比PM算法在角度估计上要稍好。
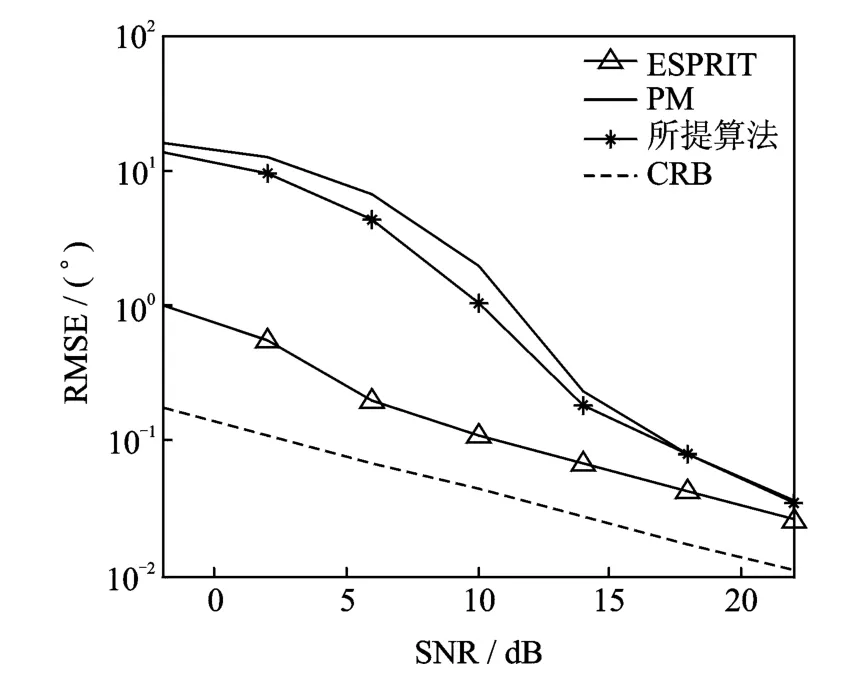
图7 相近目标下不同算法的角度估计性能对比Fig.7 Angle estimation with two closely spaced targets
5 结束语
本文提出了MIMO阵列中一种基于PM和降维变换的DOA估计方法。该算法在无需谱峰搜索的情况下获得了较好的估计性能。相比于传统的PM算法,所提的算法复杂度更低,并且估计性能更好。此外,本文推导了该算法的估计误差以及克拉美罗界。仿真结果验证了该算法的有效性。
[1]He J,Swamy M N S,Omair A M.Joint DOD and DOA estimation for MIMO array with velocity receive sensors[J].IEEE Signal Processing Letters,2011,18(7):399-402.
[2]Fishler E,Haimovich A,Blum R S,et al.MIMO radar:An idea whose time has come[C]//Proc IEEE Radar Conf.[S.l.]:IEEE,2004:71-78.
[3]Fishler E,Haimovich A,Blum R S,et al.Spatial diversity in radars models and detection performance[J].IEEE Trans Signal Process,2006,54(3):823-838.
[4]Fuhrmann D R,Antonio G S.Transmit beamforming for MIMO radar systems using partial signal correlation[C]//Proc 38th Asilomar Conf on Signals,Systems and Computers.Pacific Grove,CA,USA:IEEE,2004:295-299.
[5]Xu L,Li J,Stoica P.Adaptive techniques for MIMO radar[C]//Proc 4th Workshop on Sensor Array and Multichannel Signal Process.Waltham,UA,USE:IEEE,2006:258-262.
[6]Robey F C,Coutts S,Weikle D D,et al.MIMO radar theory and experimental results[C]//Proc 38th Asilomar Conf Signals,Systems and Computers.Pacific,Grove,CA,USA:IEEE,2004:300-304.
[7]Li J,Stoica P,Xu L,et al.On parameter identifiability of MIMO radar[J].IEEE Signal Process Lett,2007,14(12):968-971.
[8]Bekkerman I,Tabrikian J.Target detection and localization using MIMO radars and sonars[J].IEEE Trans Signal Process,2006,5(10):3873-3883.
[9]Xu L,Li J,Stoica P.Target detection and parameter estimation for MIMO radar systems[J].IEEE Trans Aeros Electro Syst,2008,44(3):927-939.
[10]Zhang J,Zhang L,Liu N.Maximal likelihood DOA estimation of MIMO radar[J].System Engineering and Electronic,2009,31(6):1292-1294.
[11]Yan H,Li J,Liao G.Multitarget identification and localization using bistatic MIMO radar systems[J].Eurasip J Adv Signal Process,2008:1-8.
[12]Xia W,He Z.Multiple-target localization and estimation of MIMO radars using capon and APES techniques[C]//2008IEEE Radar Conference Radar.[S.l.]:IEEE,2008:1-6.
[13]Zhang X,Xu D.Angle estimation in MIMO radar using reduced-dimension Capon[J].Electronic Letter,2010,46(12):860-861.
[14]Liu F,Wang J.AD-MUSIC for jointly DOA and DOD estimation in bistatic MIMO radar system[C]//2010International Conference on Computer Design And Applications (ICCDA 2010).Qin Huangdao,China:IEEE,2010:455-458.
[15]Gao X,Zhang X,Feng G,et al.On the MUSIC-derived approaches of angle estimation for bistatic MIMO radar[C]//WNIS′09International Conference on Wireless Networks and Information Systems.Shang hai,China:IEEE,2009:343-346.
[16]Zhang X,Xu L,Xu L,et al.Direction of departure(DOD)and direction of arrival(DOA)estimation in MIMO radar with reduced-dimension MUSIC[J].IEEE Communications Letters,2010,14(12):1161-1163.
[17]Bencheikh M L,Wang Y,He H.Polynomial root finding technique for joint DOA DOD estimation in bistatic MIMO radar[J].Signal Processing,2010,90(9):2723-2730.
[18]Jinli C,Hong G,Weimin S.Angle estimation using ESPRIT without pairing in MIMO radar[J].Electron Lett,2008,44(24):1422-1423.
[19]Duofang C,Baixiao C,Guodong Q.Angle estimation using ESPRIT in MIMO radar[J].Electron Lett,2008,44(12):770-771.
[20]Nion D,Sidiropoulos N D.A PARAFAC-based technique for detection and localization of multiple targets in a MIMO radar system[C]//2009IEEE International Conference on Acoustics,Speech and Signal Processing.[S.l.]:IEEE,2009:2077-2080.
[21]Nion D,Sidiropoulos N D.Adaptive algorithms to track the PARAFAC decomposition of a third-order tensor[J].IEEE Trans on Signal Proces,2009,57(6):2299-2310.
[22]Sylvie M,Alain M,Messaoud B.The propagator method for source bearing estimation[J].Signal Processing,1995,42(2):121-138.
[23]Wu Y,Liao G,So H C.A fast algorithm for 2-D direction-of-arrival estimation[J].Presented at Signal Processing,2003,83:1827-1831.
[24]Tayem N,Kwon H M.L-shape-2-D arrival angle estimation with propagator method[J].IEEE Trans on Antennas and Propagation,2005,53(5):1622-1630.
[25]StoicaP,Nehorai A.Performance study of conditional and unconditional direction-of-arrival estimation[J].IEEE Trans Signal Process,1990,38:1783-1795.
