基于DNA遗传优化的正交小波常模盲均衡算法
2014-11-17郭业才张冰龙吴彬彬
郭业才 张冰龙 吴彬彬
(南京信息工程大学电子与信息工程学院,南京,210044)
引 言
在无线通信中,通信信道复杂多变而引起的失真和有限带宽所带来的码间干扰(Inter-symbol interference,ISI)是影响通信质量的主要因素。为了提高通信质量,需要采用有效的信道均衡技术来消除码间干扰所带来的影响。与传统的自适应均衡算法相比,常模盲均衡算法(Constant modulus algorithm,CMA)由于不需要发送训练序列,极大地提高了带宽的利用率[1]。然而,对于传统的常模盲均衡算法,其收敛速度慢、均方误差大,不适合用于高速实时无线通信。文献[2,3]将正交小波变换引入到盲均衡算法中,通过正交小波变换降低输入信号的相关性,提高了盲均衡算法的收敛速度。然而这些算法都是利用常模算法的思想对均衡器权向量进行优化更新的,要求误差函数可导,并且容易陷入局部最优。
遗传算法(Genetic algorithm,GA)是以自然选择和遗传理论为基础,模拟自然界生物遗传进化进程的人工智能优化算法。遗传算法不依赖于问题的具体领域,具有很强的鲁棒性。然而传统的遗传算法收敛速度慢,而且容易早熟收敛[4-5]。DNA计算是Adleman博士1994年首次提出的。DNA计算是一种新型的计算方式,它将问题的解编码为DNA核苷酸链,再通过各种基因级操作筛选出问题的最优解。由于DNA计算和遗传算法有着天然的联系,所以研究人员将DNA计算和遗传算法相结合,提出了 DNA遗传算法[6-8],该算法能够更好地反映出生物遗传信息的表达机制,更有利于发展功能更强大、解决更复杂问题的智能优化系统。而盲均衡算法权向量初始化优化问题一直是没有能有效解决的复杂问题,如何用DNA遗传算法来解决盲均衡算法均衡器权向量初始优化问题正是本文想要解决的问题。
基于以上分析,本文将DNA遗传算法与正交小波常模盲均衡算法相结合,提出了一种基于DNA遗传优化的正交小波常模盲均衡算法(DNA-GA-WTCMA)。该算法首先对均衡器输入信号进行正交小波变换,将变换后的信号作为DNA遗传算法的输入,再由WTCMA代价函数的倒数定义DNA遗传算法的适应度函数,通过寻求适应度函数最大化过程来寻找均衡器最优初始化权向量。与正交小波常模盲均衡算法和基于遗传优化的正交小波常模盲均衡算法相比,该算法在收敛速度和稳态误差方面的性能都有所改善。
1 正交小波常模盲均衡算法
将正交小波变换引入到常模盲均衡算法中就得到了基于正交小波变换的常模盲均衡算法(Wavelet transform constant modulus blind equalization algorithm,WTCMA)。它是通过降低输入信号的相关性来提高收敛速度的。其原理如图1所示。
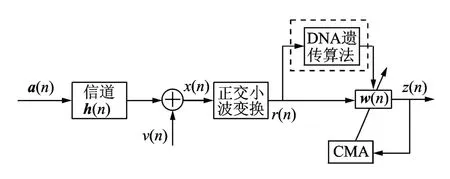
图1 正交小波常数模盲均衡算法原理Fig.1 Block diagram of orthogonal wavelet transform constant modulus blind equalization algorithm
图中a(n)为发射信号,h(n)为信道冲击响应,v(n)为信道加性高斯白噪声,x(n)为正交小波变换的输入信号,r(n)为经过正交小波变换后的信号,w(n)为均衡器的权向量,z(n)为经均衡后的输出信号

式中:Q为正交小波变换矩阵,H表示共轭转置,称为Godard常数。
WTCMA的代价函数为
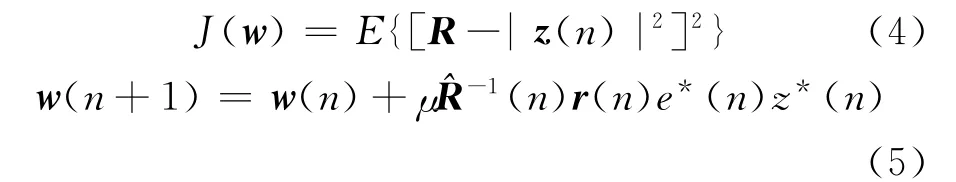
式中:*表示共轭;e(n)为误差函数,μ为步长,,其中 diag[·]表示对角矩阵分别表示rj,k(n)和sJ+1,k(n)的平均功率估计,且

式中:β为平滑因子,且0<β<1,一般取略小于1的数,rj,k(n)和sJ+1,k(n)为信号经尺度函数φj,k(n)和小波函数φJ,k(n)卷积生成的变换系数,即

式(1-8)构成了正交小波常模盲均衡算法[3]。然而,这种算法容易陷入局部最优,本文将DNA遗传算法与正交小波常模盲均衡算法相结合,进一步提高盲均衡算法的性能。
2 基于DNA遗传优化的正交小波盲均衡算法
传统的正交小波常模盲均衡算法是采用快速梯度下降搜索法对均衡器权向量进行优化的,缺乏全局搜索能力,并且要求均衡器的代价函数必须满足可导的条件。为了进一步提高均衡器的性能,本文将DNA遗传算法应用到正交小波常模盲均衡算法中,得到基于DNA遗传优化的正交小波常模盲均衡算法。
2.1 DNA遗传算法
2.1.1 DNA编码
DNA分子是生物体内存储遗传信息的重要物质,它由4种不同的核糖核苷酸分子组成通过反螺旋而形成的双链结构。一个DNA序列可以简单抽象为由腺嘌呤(A)、鸟嘌呤(G)、胞嘧啶(C)和胸腺嘧啶(T)4种碱基组成的碱基串。本文采用A,G,C,T四种碱基对盲均衡算法的权向量进行编码,此编码空间为E={A,G,C,T}l,其中l为DNA序列的长度。由于这种DNA编码方式不能被计算机直接处理,因此采用0,1,2,3这4个数字分别对应4种DNA碱基,其编码空间为E={0,1,2,3}l,这种映射关系总共有24中可能情况。在这些编码方式中,采用的映射方式为:0123/CGAT,同时碱基的数字编码也要体现互补碱基对之间的配对规律,即,0与1互补配对,A与T互补配对。通过这种编码方式就能把一段DNA序列表示为一个数字序列,便于计算机处理[6]。通过将盲均衡算法权向量寻优问题的解表示为相应的DNA链,有利于设计操作算子以加快收敛速度。
2.1.2 交叉操作
交叉操作是模仿自然界中生物有性繁殖基因重组的过程。不同的交叉操作不仅提高了子代种群的质量,而且还增强了种群中个体的多样性。
(1)置换交叉算子
随机在种群中挑选两个用于置换交叉操作的父体,在每个父体中分别随机选取碱基数目相等的一段基因序列片段,然后把选取的基因片段相互置换,产生两个新个体。
(2)转位交叉算子
和置换交叉算子不同,转位交叉算子是对单个父体操作的。转位交叉操作的发生概率是固定的。对于种群中所有个体,随机选择一个个体作为父体,对于被选中的个体,随机选取一段碱基序列并将其剪切下来,在该父体中选择一个新位置将剪切下来的基因片段插入其基因序列中,得到新个体。
(3)重构交叉算子
重构交叉算子目的是改变优秀个体的相似性而设置的,因此父体的选择不是随机的。选择两个相似度较大的优秀个体,首先在父体A的后半部分随机选择一段碱基序列R,经切除后粘贴到父体B序列的前端,由于在DNA遗传算法中,所有个体碱基数目是相同的,因此将父体B的尾部多出来的碱基序列切除,随机生成一段与序列R等长度的碱基序列,粘贴到父体A的尾部,经过重构交叉操作就得到两个相似度较小的个体,同时子代个体也保留了父体的优秀基因[6]。
2.1.3 变异操作
变异操作主要是为了保持种群一定程度的多样性,避免算法陷入局部最优。本文采用自适应变异操作,即变异概率随着进化代数的增加而自适应发生变化。DNA遗传算法变异操作与遗传算法中的变异操作相类似,区别在于,DNA遗传算法由于个体是用DNA碱基序列编码表示的,因此序列中某位碱基可能会变异成另外其他3种碱基,并且变异到某种碱基是随机的。根据生物学原理,同一个DNA碱基序列的不同位置存在“热点区域”和“冷点区域”,并且在“热点区域”内的碱基变异概率比“冷点区域”内的碱基变异概率大。对于DNA遗传算法而言,在进化不同阶段、不同位置碱基变异对盲均衡算法权向量初始优化问题的最终解产生影响。在进化的初始阶段,为了能够快速地向最优解移动,需要个体DNA序列的高位有较大的变异概率;在进化的结束阶段,为了实现对最优解精确搜索,需要DNA序列的高位部分有较低的变异概率,以保持解的稳定,同时序列的尾部要有较大的变异概率,以便能够快速精确地搜索到最优解。根据以上分析,将DNA序列的前半部分定义为高位部分,后半部分定义为低位序列,并设置不同的变异概率分别为[9-10]

式中:pml和pmh分别代表低位部分和高位部分的变异概率,a1表示高位部分的最终变异概率和低位部分初始时刻的变异概率值,a1=0.02;b1表示变异概率的变化范围,b1=0.2;g表示当前的进化代数,g0表示变异概率变化最大时的进化代数值,g0=50;a是变异概率最大时的斜率,a=0.2。变异概率曲线如图2所示。

图2 DNA碱基序列变异概率Fig.2 DNA nucleotide sequence mutation probability
2.2 基于DNA遗传优化正交小波盲均衡算法
2.2.1 确定适应度函数
将均衡器权向量作为DNA遗传算法的决策变量,考虑到盲均衡算法的特点,设计初始种群Chrom=[w1,w2,…,wM],M为种群个体数量,wm,1≤m≤M对应一个均衡器权向量。设接收信号序列的长度为N,利用时间平均代替统计平均,则WTCMA的代价函数可写为
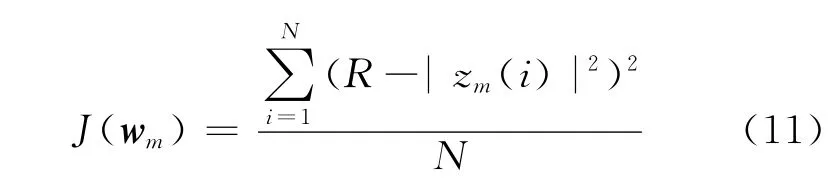
式中:m表示均衡器权向量个体的序号,zm(i)为每个均衡器权向量个体的输出信号,式(11)作为DNA遗传算法的目标函数,与其全局最小值对应的个体就是要求的最佳个体,然后将其解码后作为均衡器的初始权向量。本文将选择适应度值最大的个体作为WTCMA权向量寻优问题的最终解。由于J(wm)>0,因此将适应度函数定义为代价函数的倒数,即

式中:b表示比例系数。
2.2.2 算法步骤
步骤1 首先按照2.1.1节的编码方式将已经初始化的均衡器权向量编码为DNA核苷酸链,设置种群规模为M个个体。将经过正交小波变换后的信号作为DNA遗传算法的输入信号,计算每个个体的适应度值。根据个体适应度值的大小将所有个体进行排序,前一半个体为优质种群,后一半个体为劣质种群,个体适应度值最大的为当前种群中的最优个体,并作为精英个体保留。
步骤2 在优质种群中随机选取用于操作的父体执行交叉操作,对被选中的父体分别执行置换交叉和转位交叉的概率为p1和p2。若父体均未执行置换交叉和转位交叉操作,则按重构交叉概率p3执行重构交叉操作。重复以上交叉操作直到产生M/2新个体,然后将这M/2新个体放入到原种群中,得到3M/2个个体。
步骤3 在新得到的种群中执行自适应动态变异操作。用变异后的新个体取代原个体,变异操作完成后,重复执行M-1次联赛选择操作,挑选出M-1个个体,与精英个体一起组成种群规模为M的新种群,种群进化代数加1,然后计算种群中每个个体的适应度值。
步骤4 判断是否达到进化终止条件。算法的终止用最大进化代数来判断,如果当前进化代数小于最大进化代数,则继续对新种群分组,完成步骤2~步骤4,直到当前进化代数大于最大进化代数为止。
步骤5 如果当前进化代数大于最大进化代数,则将种群中适应度值最大的个体作为最优个体输出,并将其解码,解码后的值作为均衡器的初始权向量。算法流程如图3所示。
3 仿真实验
为了检验DNA-GA-WTCMA的性能,以正交小波盲均衡算法、基于遗传优化的正交小波盲均衡算法和文献[4]提出的基于混合遗传优化正交小波盲均衡算法(Hybrid blind equalization algorithm based on genetic algorithm and wavelet transform,HGA-WTCMA)为比较对象,进行仿真实验。仿真实验采用16PSK信号,信道噪声采用高斯白噪声,信道h=[0.313 2-0.104 0 0.890 8 0.313 4],发射信号为16PSK,均衡器权长为16,信噪比为25dB,训练样本个数N=12 000。

图3 基于DNA遗传优化的正交小波盲均衡算法流程图Fig.3 Flow diagram of orthogonal wavelet transform constant modulus blind equalization algorithm based on the optimization of DNA genetic algorithm
WTCMA第10个抽头系数设置为1,其他的抽头系数均取0,步长取0.000 005。本实验中正交小波均采用Db4小波,分解层数为2层,β取值为0.99,功率初始化值为10。
HGA-WTCMA和GA-WTCMA的种群规模取30,交叉操作采用两点交叉,交叉概率取0.65;变异操作采用非均匀变异,变异概率取0.06。选择操作采用精英选择和轮盘赌选择结合的选择操作。终止进化代数为100代。
DNA-GA-WTCMA种群规模取30,置换交叉概率p1=0.8,转位交叉概率p2=0.5,重构交叉概率p3=0.2。变异操作按照2.1.3节所述的自适应变异概率执行。最大进化代数为100代。
图4表明,DNA-GA-WTCMA的收敛速度较快,均方误差收敛速度比 WTCMA,GA-WTCMA和 HGA-WTCMA 的 收 敛 速 度 快,DNA-GAWTCMA收敛速度比GA-WTCMA收敛速度大约快1 000步。从稳态误差上看,DNA-GA-WTC-MA的稳态误差比HGA-WTCMA小约1dB,比GA-WTCMA小2dB,比WTCMA小约5dB。由于DNA-GA-WTCMA采用自适应动态变异和新型的个体交叉方案,因此算法的收敛速度得到了很大的提高,同时减小了算法陷入局部最优解的可能。从星座图上看,DNA-GA-WTCMA输出的星座图比 WTCMA,GA-WTCMA 和 HGA-WTCMA输出的星座图更清晰、紧凑。实验采用300次蒙特卡洛仿真。仿真结果如图5所示。
可见,将DNA遗传优化算法应用于正交小波变换盲均衡算法中,可以显著提高盲均衡算法的收敛速度和减少均方稳态误差。
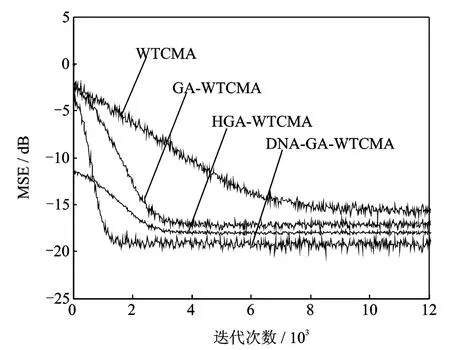
图4 均方误差迭代曲线Fig.4 Mean square error iterative carve

图5 WTCMA输出星座图Fig.5 Output constellation
4 结束语
本文提出了一种基于DNA遗传优化正交小波变换常模盲均衡算法,该算法将DNA计算与遗传算法相结合,并且应用到正交小波变换常模盲均衡算法中,通过采用DNA核苷酸对要求的问题潜在解进行编码,再对编码后的DNA链采取交叉、变异等基因级操作,可以提高正交小波常模盲均衡算法的收敛速度,并且降低了稳态误差。仿真结果表明,与原有的基于遗传算法优化的正交小波变换常模盲均衡算法相比,该算法具有更快的收敛速度和更小的稳态误差,输出的星座图更加清晰、紧凑,因此该算法对通信信号处理研究具有一定的参考价值。
[1]郭业才.自适应盲均衡技术[M].合肥:合肥工业大学出版社,2007:17-25.Guo Yecai.Adaptive blind equalization technique[M].Hefei:Hefei University of Technology Publishing House,2007:17-25.
[2]韩迎鸽,郭业才,吴造林,等.基于正交小波变换的多模盲均衡器设计与算法仿真研究[J].仪器仪表学报,2008,29(7):1441-1445.Han Yingge,Guo Yecai,Wu Zaolin,et al.Design and algorithm simulation of orthogonal wavelet transform based multimodulus blind equalizer[J].Chinese Journal of Scientific Instrument,2008,29(7):1441-1445.
[3]郭业才,杨超.基于正交小波变换的分数间隔盲均衡算法[J].数据采集与处理,2011,26(3):247-252.Guo Yecai,Yang Chao.Blind fractionally spaced equalization algorithm based on orthogonal wavelet transform[J].Journal of Data Acquisition and Processing,2011,26(3):247-252.
[4]郭业才,樊康,徐文才,等.基于混合遗传优化的正交小波变换盲均衡算法[J].数据采集与处理,2011,26(5):503-507.Guo Yecai,Fan Kang,Xu Wencai,et al.Hybrid blind equalization algorithm based on genetic algorithm and wavelet transform[J].Journal of Data Acquisition and Processing,2011,26(5):503-507.
[5]廖娟,郭业才,刘振兴,等.基于遗传优化的正交小波分数间隔盲均衡算法[J].兵工学报,2011,32(3):268-273.Liao Juan,Guo Yecai,Liu Zhenxing,et al.A fractionally spaced blind equalization algorithm based on orthogonal wavelet transform and genetic optimization[J].Acta Arm Amentarii,2011,32(3):268-273.
[6]陈宵.DNA遗传算法应用与研究[D].杭州:浙江大学,2010:19-24.Chen Xiao.Research on DNA genetic algorithms and applications[D].Hangzhou,China:Zhejiang University,2010:19-24.
[7]Zhao Yuanqing,Jin Xianhua,Liu Yong.The preemptive EDF optimization based on DNA-genetic algorithm[C]∥2nd Conference on Environmental Science and Information Application Technology.Wuhan,China:IEEE,2010:121-124.
[8]Li Yongjie,Lei Jie.A feasible solution to the beamangle-optimization problem in radiotherapy planning with a DNA-based genetic algorithm [J].IEEE Transactions on Biomedical Engineering,2010,57(3):499-508.
[9]Zhang Duan,Xia Yanling,He Xiongxiong,et al.Multi-step evolution strategy based DNA genetic algorithm for parameters estimating[C]∥ The 4th International Conference on Intelligent Control and Information Processing (ICICIP).Beijing,China:IEEE,2013:828-835.
[10]Wang Kangtai,Wang Ning.A novel RNA genetic algorithm for parameter estimation of dynamic systems[J].Chemical Engineering Research and Design,2010,88(11):1485-1493.
