一种基于FFT低复杂度的信道盲辨识算法
2014-11-17孙有铭刘洛琨杨正举
孙有铭 刘洛琨 杨正举 郭 虹
(解放军信息工程大学信息系统工程学院,郑州,450002)
引 言
随着移动通信的迅猛发展,对于高容量、高可靠性传输的追求使得不需要训练序列的信道盲辨识技术非常具有吸引力。盲辨识技术由于其节省了信道资源,提高了信道传输效率受到了信号处理领域学者的广泛重视。目前盲辨识算法主要分为基于高阶统计量的传统方法和基于循环平稳二阶统计量的方法两大类。随着Tong等人开创性地提出利用二阶循环统计量进行时不变信道盲辨识[1]之后出现了一系列的盲辨识算法[2-7]。
文献[2]提出了一种利用接收端过采样之后形成的单输入多输出(Single input multiple output,SIMO)信道各个子信道的交叉相关(Cross-relation,CR)性质建立线性方程,从而获得信道向量闭式解的CR算法。文献[3]提出了一种利用接收数据的自相关矩阵可划分为相互正交的“信号空间”和“噪声空间”,利用噪声子空间和信道矩阵的正交性来求解信道系数的子空间方法(Subspace,SS)。文献[4]在文献[3]的基础上提出了一种最小噪声子空间方法(Minimum noise subspace,MNS),巧妙地利用含有最小冗余度的子信道对来求解信道系数,降低了SS算法的运算复杂度。文献[5]将文献[4]的思想推广到了CR算法中,提出了一种最小CR算法(Minimum cross relation,MCR)。
传统二阶循环统计量盲辨识算法在短突发信号条件下性能恶化甚至失效,算法对于观测数据的长度有一定要求[8]。为了解决小样本观测数据条件下的信道盲辨识问题,文献[6]提出了一种将CR算法通过FFT变换到离散频域来求解信道系数的BI-FFT算法,在短突发的小样本观测数据(M+1≤Ns<3M+1,M表示信道阶数)和较高信噪比条件下获得了良好的性能。但是文献[6]采用的是标准CR算法,当过采样率越大时运算的复杂度也迅速提升。本文在BI-FFT算法基础上提出了一种只利用最小冗余信息建立频域CR方程的F-MCR算法,该算法既减小了BI-FFT算法的运算复杂度又达到了与原有算法相当的性能。
针对现有的阶数估计算法(包括Liavas算法[9]、新颖的有效阶数估计算法(Novel effective channel order estimation,NECOE)[10]以及基于子空间信道矩阵迭代的阶数算法[1]等大多建立在自相关矩阵的奇异值分析的基础上,对于观测数据量有一定要求,在短突发(小样本)接收数据情况下,以上算法失效。本文结合F-MCR算法中的矩阵Fy的秩信息给出了一种可行的快速阶数估计算法。
本文中,nullspace(A)表示矩阵A的零空间维度,deg(p(x))表示多项式p(x)中的x最高次数,[·]T,[·]H,⊗,(·)+,‖·‖2分别表示转置、共轭转置、卷积、Moore-Penrose伪逆运算和取2范数操作。
1 信道模型和CR算法
考虑单天线以L倍波特率过采样或用L根天线以波特率接收[1],可得到SIMO信道。在算法建模中将其等效为有限阶支撑的M阶FIR信道。
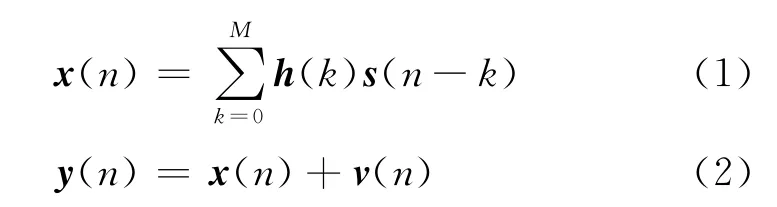
式中:s(n)是统计独立发射信号序列,x(n)=[x1(n),x2(n),…,xL(n)]T为无噪的观测向量,h(n)=[h1(n),h2(n),…,hL(n)]T,其中hi(n)(i=1,…,L)为第i条信道的冲激响应,可简记为h=(n),v2(n),…,vM(n)]T为方差为且独立于发送信号的高斯白噪声,y(n)为迭加了噪声后的观测向量。
无噪情况下,在信道阶数M已知时信道i的输出xi(n)和信道j的输出xj(n)存在以下CR关系
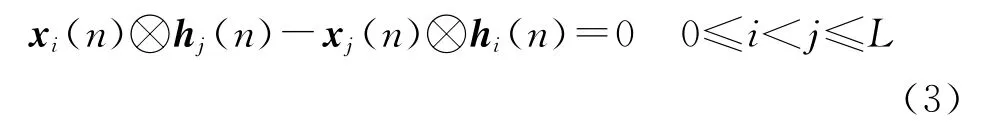
式(3)写成如下矩阵形式

式中

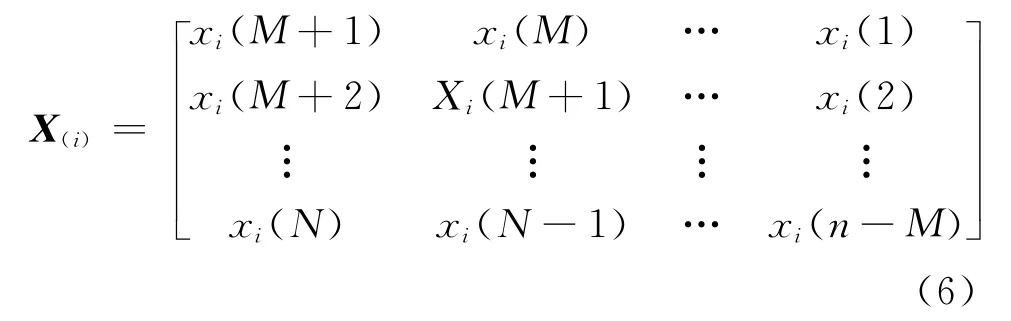
则关于所有子信道对(i,j),其中i,j=1,2,…,L,i≠j,可以得到如下方程组

式中
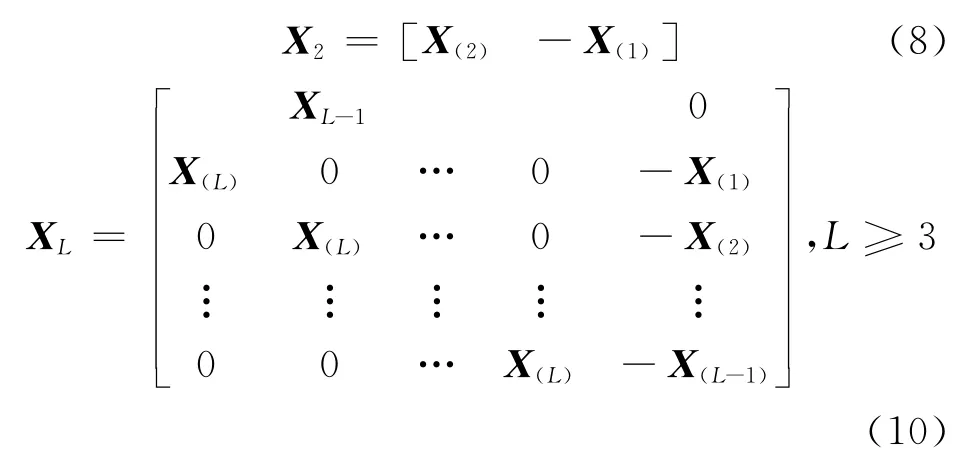
实际中噪声的影响不可避免。假设噪声是加性高斯白噪声,那么式(9)修正为

式中:YL是由迭加了噪声影响的实际接收数据构成,而δ则是相对应的误差向量。可以用最小二乘法求解方程并施加范数约束后获得信道向量的闭式解
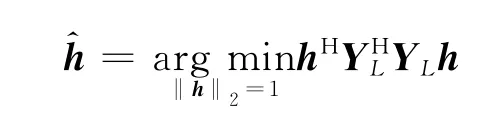
2 F-MCR算法
2.1 算法描述
文献[5]提出的最小冗余度的 MCR算法和MNS[4]算法类似,主要是通过一种树形的结构来构建,这种树形结构既反映出了信道间的差异性又具有最小的信息冗余度。
定理1 在SIMO系统中,首先从L个输出x1,…,xL中选出L-1个不同的组,每组是两个子信道输出数据的组合,L-1个组合可以构成一个树的结构。把每个子信道的输出看作一个树的结点,共有L个结点,使树形结构具有最小冗余度必须遵循连接所有节点并且不构成回路的原则。依据此树形结构构建的CR方程具有最小冗余度。
定理1的证明参见文献[5],显然树形结构的连接的方法并不唯一。图1所示为一个5倍波特率采样的SIMO信道的树形结构的选取,[1,2],[1,3],[2,4],[2,5]的输出子信道组就可以列出最小冗余度的CR方程用来求解信道系数。
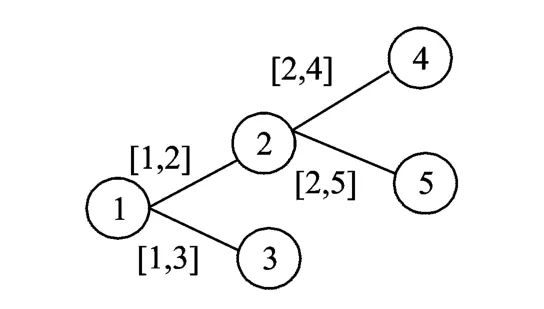
图1 系统输出树形图Fig.1 Tree diagram of system output
标准CR算法中,需要运用到所有的子信道输出对,即L倍过采的SIMO信道就需要用到L(L-1)/2个信道对构成CR方程,L越大,随之形成的YL矩阵也就越庞大,计算量也会随之增加。但是在MCR算法中,只需要用到L-1个信道对,当过采样L>2时,计算量明显减少。
假定在无噪声情况下,每个子信道的输出序列xi(n)的长度为Ns+M,其中1≤i≤L,对xi(n)×hj(n)-xj(n)×hi(n)=0,0≤i<j≤L等式两边进行N点FFT变换(N≥Ns+M),可得离散频域表达式

式(12)可以写为
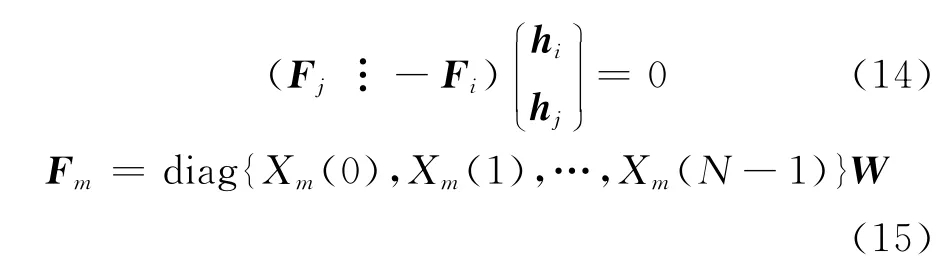
式中
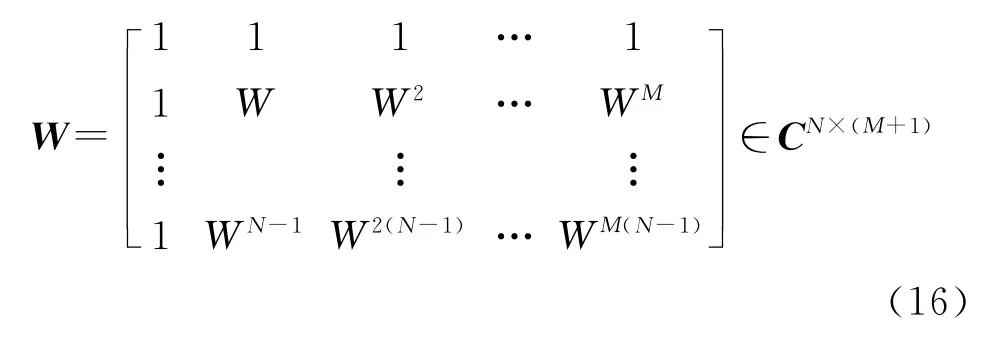
式中:W=e-j2π/N,并定义Fi,j=其中Fj位于i个矩阵块的位置,而Fi位于第j个矩阵块的位置。其中将符合MCR中最小冗余度的的子信道对[i,j]组成Fi,j矩阵,再将Fi,j构 成 一 个 大 的 矩 阵 块Fx∈CN(L-1)×L(M+1)

在考虑噪声影响后,Fx将由接收的含噪数据进行FFT后构成的Fy来近似,则可修正为

其中ε为噪声引起的误差矩阵,对式利用最小二乘方法求解并施加范数约束可得

2.2 阶数估计算法
现假设信道阶数M未知,仅阶数的上界MU已知。那么原来的精确阶数估计下的Fy写成可以根据Fy(M)的零空间的维度来进行阶数估计。
定理2零空间特性定理
(1)=M,是列秩亏为1,有唯一线性解,即nullspace)=1。
(3)M+1≤≤MU,是列秩亏为-M+1,即nullspace=-M+1
证明:文献[6]中已经给出(1)和(2)的分析,这里不再赘述,以下将给出情况(3)的证明如下:
当=M+ΔM,ΔM=1,2…时,由于的选择决定了WM矩阵,即相当于选取了DFT矩阵的前=M+ΔM列。式(14)可以写成
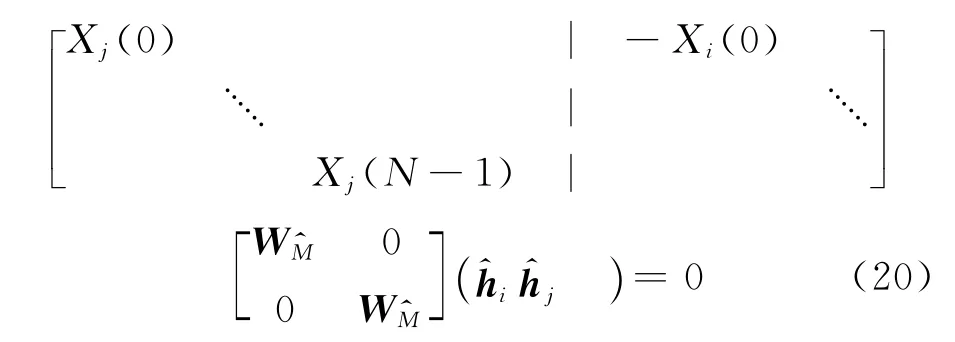
此时估计得到的和都是×1的列向量,就是对进行N点DFT,由此可得的Z域形式(Z),其deg(Z))≤;同理,deg((Z))≤。式(20)可等价于以下Z变换形式

假设输入符号要满足以下条件,其DFT形式下的S(k)≠0,k=0,1,…,N-1[6],式(21)可简化为
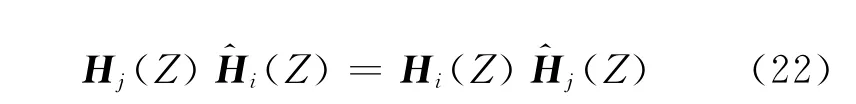
由于子信道之间满足互质条件,即zeros(Hj(Z))∩zeros(Hi(Z))=0,且满足Hi(Z),Hj(Z)≠0,又有(Z)),那么可得zeros(Hj(Z))⊆zeros(Hj(Z)),由于deg(Hi(Z))=M,则(Z),其中0≤deg(c(z))≤ΔM。由式(21)可得可知c(z)为过估计引入的公共零点。得到的形式和文献[12]中的形式一致,可知解空间的维度为ΔM+1,即nullspace=由于DFT矩阵的特殊形式,可知01×(ΔM-a)]T,a=0,1,…,ΔM为解空间的基,得证。
定理2表明矩阵在信道阶数过估计时获得不是一维线性解而是一个解空间,其维度为+1。由于噪声的影响,在过估计情况下属于的零奇异值不再为零,本文将采用矩阵相邻的两个奇异值比值的大小来判断零奇异值和非零奇异值之间的分界线。设维度为(N(L-1))×L+1)的Fy(M)的奇异值为

令ri表示相邻奇异值λi-1和λi之比

现给出一个信道阶数快速搜索算法,阶数搜索过程如下。
(1)选择一个较大的阶数估计值,确定的零空间的维度是否为1,即最大r的位置后面的较小的比值个数。若维度为1则搜索结束。若零空间维度不为1跳入步骤(2)。
(2)零空间维度不为1,即最大的r的后面的小的比值的个数为d(d为正整数),则将-d作为新的阶数估计值,并跳入步骤(1)。
2.3 算法流程
综上所述,本文算法步骤如下:
(1)选取一个较大的阶数估计值,通过进行奇异值分解,利用给出的阶数估计算法从的零空间维度估计出精确信道阶数M。
(2)选取合适的FFT点数N满足N≥Ns+M,对每个子信道的输出向量xm进行FFT变换并计算Fm矩阵。
(3)根据树形结构找到最小冗余度的L-1个信道对[i,j],1≤i,j≤L,并由相应信道对的数据组成Fi,j,再将Fi,j组成Fy矩阵。
(4)通过式(19)求解得到信道向量的闭式解。
2.4 算法复杂度
由于BI-FFT算法中没有阶数估计环节,这里仅考虑在阶数M已知情况下的复杂度分析,通过F-MCR和BI-FFT算法在对Fy矩阵的构建不难发现,BI-FFT 算法下的Fy(BI-FFT)的维度是(NL(L-1)/2)×L(M+1),而F-MCR算法下的Fy(F-MCR)的维度是(N(L-1))×L(M+1)。参考文献[13]的运算复杂度分析方法,为简化分析主要考虑算法中运算复杂度最高的奇异值分解部分,对于BI-FFT算法大约需要O{NM2L4},而 F-MCR只需约O{NM2L3}。当L越大,这种计算量的差异性就会越明显。
3 仿真实验
为了验证算法的性能,选取SS算法和文献[6]提出的BI-FFT算法做性能对比。仿真时采用文献[1]中给出过采率L=4时形成的SIMO信道,信道阶数M=4,信道系数如表1所示。

表1 含4个子信道的SIMO信道系数Table 1 Channel coefficients of a SIMO channel with 4sub-channels
发射信号为均匀分布的QPSK信号,迭加的噪声为高斯白噪声。辨识结果用归一化均方误差(Normalized root-mean-square error,NRMSE)进行评价。NRMSE的定义如下

其中:Nr为蒙特卡罗实验次数,在本次仿真试验中设定Nr=100,hi是第i次实验的辨识结果。
3.1 信道估计性能随信噪比变化实验
为了验证本文信道算法在小样本观测数据条件下的有效性,选取发射端发送符号数量Ns=10,即每个子信道可用的数据为Ns+M,设定FFT变换的点数N=16。出于公平性,此处实验均假定信道阶数已知。从图2可以明显看到SS算法已经完全失效,而本文提出的F-MCR和BI-FFT算法性能相当,可见F-MCR算法在降低BI-FFT算法的运算复杂度的同时并没有引起性能恶化。图2的结果中可以得知小样本观测数据条件下传统的基于二阶统计量的盲辨识算法性能恶化甚至失效。文献[8]证明传统算法至少需要满足Ns≥3M+1,而基于BI-FFT算法和F-MCR算法只需满足Ns≥M+1。

图2 SNR-NRMSE曲线图Fig.2 Performance of NRMSE with changing
3.2 阶数估计算法性能随信噪比变化实验
图3为在表1中所给信道条件下Liavas算法、NECOE算法与本文所提阶数算法的阶数估计正确率随信噪比变化图。其中本文所提算法中参数同实验3.1,Liavas算法和NECOE算法中接收符号数均为200。从图3中可知,Liavas算法在SNR≥24dB估计正确率达到100%,而NECOE算法在SNR≥28dB估计正确率达到100%。虽然本文所提阶数估计算法也需在SNR≥28dB估计正确率达到100%,但在同样的短突发小样本条件下,Liavas算法和NECOE算法完全失效。
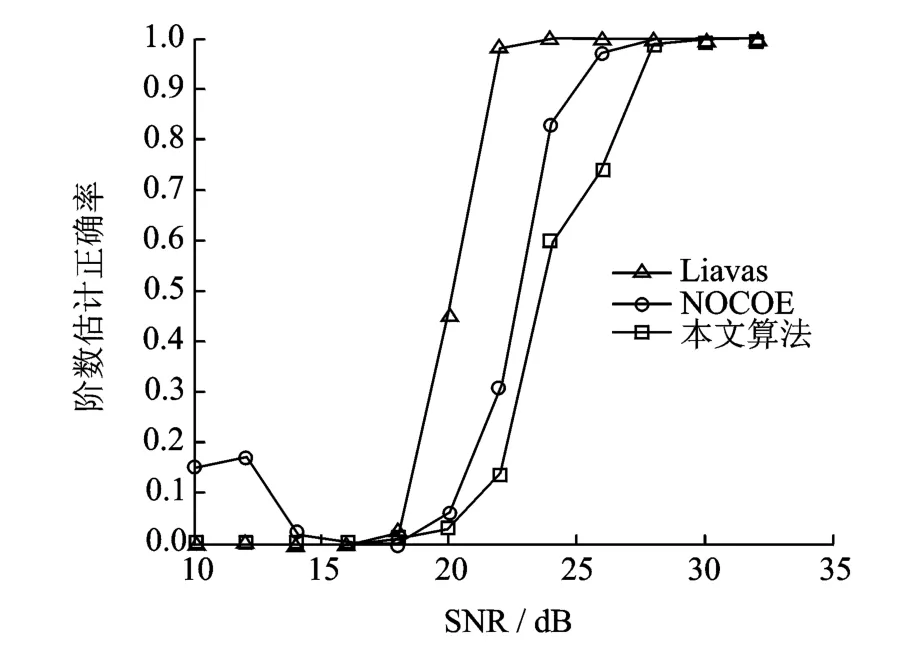
图3 SNR-阶数估计正确率曲线图Fig.3 Probability of correct channel order detection with changing SNR
4 结束语
本文提出了一种改进的基于FFT的盲辨识算法(F-MCR),该算法充分利用MCR算法只需利用最小冗余度的信息建立线性方程即可估计信道的特性,将其经过FFT后再求得信道向量闭式解,并给出了一个快速阶数搜索的方法。理论分析和仿真表明:该算法在较高信噪比和样本数目较小时性能明显优于经典的二阶统计量盲辨识算法,较BIFFT算法的复杂度明显降低而性能几乎相当,同时提升了对于信道阶数估计误差的鲁棒性。
[1]Tong L,Xu G,Kailath T.Blind identification and equalization based on second-order statisics:a time domin approach[J].IEEE Trans on Inform Theory,1994,40:340-349.
[2]Xu G,Liu H,Tong L,et al.A least squares approach to blind channel identification[J].IEEE Trans on Signal Processing,1995,43(12):2982-2993.
[3]Moulines E,Duhannel P,Cardoso J F,et al.Subspace methods for the blind identification of multichannel FIR filters[J].IEEE Trans on Signal Processing,1995,43(2):516-525.
[4]Hua Y,Abed-Meraim K,Wax M.Blind system identification using minimum noise subspace [C]//8 th IEEE Workshop on SSAP.Corfu,Greece:[s.n.],1996:308-311.
[5]Aissa-El-Bey A,Grebici M,Abed-Meraim K.et al.Blind system identification using cross-relation methods:further results and developments[J].7th International Symposium on Signal Processing and Its Applications,2003,1:649-652.
[6]Wang S,Manton J,Tay D B H,et al.An FFT-based method for bind identification of FIR SIMO channels[J].IEEE Signal Processing Letters,2007,14(7):437-440.
[7]李森,邱天爽.基于鲁棒性协方差矩阵估计的盲信道识别方法[J].数据采集与处理,2010,25(5):549-553.Li Sen,Qiu Tianshuang.Blind channel identification based on robust covariance matrix estimation [J].Journal of Data Acquisition and Processing,2010,25(5),549-553.
[8]Hua Y,Wax M.Strict identifiability of multiple FIR channels driven by an unkown arbitrary sequence[J].IEEE Trans Signal Processing ,1996,44(3):756-759.
[9]Liavas A P,Regalia P.On the behavior of information theoretic criteria for model order selection [J].IEEE Transactions on Signal Processing,2001,49(8):1689-1695.
[10]代松银,袁嗣杰,董书攀.基于子空间分解的信道阶数估计算法[J].电子学报,2010,38(6),1245-1248.Dai Songyin,Yuan Sijie,Dong Shupan.Effective channel order estimation based on subspace decomposition[J].Chinese Journal of Electronics,2010,38(6):1245-1248.
[11]孙有铭,刘洛琨,崔波,等.基于子空间信道矩阵迭代的阶数估计算法[J].电子与信息学报,2013,35(2):432-437.Sun Youming,Liu Luokun,Cui Bo,et al.Channel order estimation algorithm based on subspace channel matrix recursion[J].Journal of Electronics &Information Technology,2013,35(2):432-437.
[12]Gunther J,Swindlehurst A.On the use of kernel structure for blind equalization[J].IEEE Trans Signal Process,2000,48(3),799-809.
[13]Hua Y.Fast maximum likelihood for blind identification of multiple FIR channels[J].IEEE Trans Signal Processing,1996,44(3):661-672.
