数字控制电压调整器模块的建模分析

1 引言

适用于未来微处理器的电压调整模块（Voltage RegulatorModule,VRM）是一种特殊的负载点（PointofLoad,POL）变换器，它有很高的性能要求：低输出电压（0.8～1.6V），高负载电流（可达150A）以及快速的动态响应（负载电流变化率可达2A/ns）[1,2]。

现如今，主流的VRM电路拓扑是多相的Buck变换器[3-5]。但是，随着开关频率的提高，传统的多相Buck变换器会遇到很多问题：开关损耗高、驱动损耗高以及同步整流管的体二极管损耗高等。所以，为能使工作在较高开关频率时有相对较高的效率，文献[6]提出了一种运用在VRM上的零电压开关（ZeroVoltageSwitching,ZVS）自驱非隔离全桥变换器。所有的MOS管都实现ZVS以减少开关损耗。变压器的引入使变换器占空比得到拓展，导致MOS管开关损耗和体二极管反向恢复损耗进一步降低。同步整流管（SynchronousRectifier,SR）自驱的观念，即变压器二次电压或其电压的一部分用作整流管的驱动已被广泛运用[7-10]。同步整流管自驱的好处是：驱动电路简单、部分驱动的能量可再利用以达到低损耗，高效率的目的等。

虽然在低压、大电流、高频率的运用场合，现在仍多使用传统的模拟控制器，但随着电力电子技术的不断发展，功率变换器向着小型化、模块化和智能化发展[11,12]。传统的模拟控制已不能满足要求，因此数字控制变换器是发展的必然趋势。数字控制器是个很有前景的研究课题，它自身有很多优势：可编程、低功耗、可节省空间的使用、控制器整体的鲁棒性好，即对寄生参数变化不敏感、易于实现先进和复杂的控制策略等。为了提高功率密度和动态特性，变换器的开关频率越来越高，目前已达1MHz甚至更高。超高的开关频率会给数字控制带来新的问题。由于量化误差的存在，可能产生有限环振荡，影响系统的稳定性。另外，由于数模转换器（Analog to Digital Converter, ADC）采样时间和数字电路计算时间的存在，反馈系统中存在比较大的时间延迟，如果不能很好的建模和补偿，会严重损害系统的动态特性。本研究是在目前数字电路小信号模型的基础上，研究反馈回路上每一个环节对时间延迟的影响，从整体上得到一个完整准确的数字控制变换器小信号模型，以此来指导整个变换器控制补偿的设计[13-17]。

数字控制的12VZVS自驱VRM包括了主电路和控制电路，其中主电路部分是一个模拟系统，而数字控制部分是数模混合系统。图1给出了数字控制VRM的系统框图，点划线部分是数字控制器的内部结构。电压和电流的ADC会将采样回来的电压和电流模拟信号转换成离散值，所有的补偿和计算等都是在数字的离散形式下完成的。然后通过数字脉宽调制器（Digital Pulse Width Modulation,DPWM），将离散的占空比值再转换成模拟信号用以驱动开关管。

图1 12VZVS自驱VRM的系统框图Fig.1 System diagram of 12V ZVS self-driven VRM

因此要对数字控制VRM进行很好的控制，必须对其主电路和控制电路进行建模分析。另外还设计了自适应电压定位（Adaptive Voltage Positioning，AVP）环路以保证电路实现AVP。

本文将详细给出数字控制12VZVS自驱VRM的主电路和数字控制电路的小信号模型，并依此设计AVP环路，再通过仿真和实验结果来验证此设计方法。

2 主功率电路小信号模型的建立

12VZVS自驱VRM的主电路（图2）本质上是Buck型全桥直流变换器，它的小信号模型与多相Buck变换器类似。图3给出了12VZVS自驱VRM与两相交错并联Buck电路的对应关系。图中，12V自驱VRM中的Q2和Q4管分别对应两相Buck中的Q2和Q1管；同步整流管S1和S2分别对应到两相Buck中的S1和S2管。另外，12V自驱VRM中，Q1和Q3管的驱动信号与Q2和Q4管的互补。

图2 12V零电压开关自驱电压调整模块Fig.2 12VZVSself-drivenVRM

图3 两相Buck和12V自驱VRM的比较Fig.3 Comparison between 2-phase Buck and 12V ZVSself-driven VRM

这两个电路小信号模型的主要区别在于12V自驱VRM中存在变压器的漏感，它的功能相当于一个阻尼电阻。由于采用PCB绕组，所以漏感值较小，其作用可以忽略。因此可以借鉴多相Buck主电路

模型推导的方式来推导12V自驱VRM主电路模型。

图4是12VZVS自驱VRM的小信号模型。

图4 12VZVS自驱VRM的小信号模型Fig.4 Small signal model of 12V ZVS self-driven VRM

图中，Gii是电感电流iL相对负载电流io的传递函数。Gid是电感电流iL相对占空比d的传递函数。FM模拟了电感电流的脉动效应。Gi代表电流的检测，值通常取检测电阻Ri。Gcon是电压回路补偿器的传递函数。

这里，Leq是等效的滤波电感，DCReq是其等效的直流电阻。由于是四相交错并联工作，因此Leq是单相滤波电感的四分之一，DCReq是单相直流电阻的四分之一。

3 数字控制器小信号模型的建立

3.1 抗混滤波器小信号模型的建立

图5给出了没有限制带宽的采样信号频谱图。经过采样之后，信号的基本频谱会在采样频率的谐波频率上重复延拓，诸如±fs，±2fs等。如果信号的频谱不受限制，就会产生混叠效应。混叠效应会使得采样后的信号修复变得困难。为减小这种效应的影响，加入了一个抗混滤波器。图6给出了加入抗混滤波器后采样信号的频谱。这个滤波器的目的是消除采样信号高于奈奎斯特频率（采样频率的一半）的部分。数字控制器中，一阶低通滤波器可用作抗混滤波器。它的传递函数表达式为

图5 未限制带宽信号的频谱Fig.5 Spectrum of an unlimited band signal

图6 加入抗混滤波器后信号的频谱Fig.6 Spectrum of an unlimited band signal withanti-aliasing filter

3.2 电压和电流ADC小信号模型的建立

图1中电压和电流采样均需通过ADC将模拟信号转换成数字信号，电压和电流ADC的电路结构一样。图7是ADC的模型，它包括一个采样器、一个延时器以及一个数字转换器。

图7 模数转换器的经典模型Fig.7 Classical Model of an analog to digital converter

ADC的小信号模型可以分成两部分。第一部分包括采样和延时单元，表现出纯粹的延时功能。而在整个数字控制系统中，不仅仅ADC存在延时，计算以及DPWM都存在延时，在此所有延时都统一起来考虑，其表达式如下

式中，Td表示整个数字控制系统的延时时间，即从输出采样到占空比作用的延时时间，包括ADC、计算以及DPWM时间。

数字补偿器中，电压和电流的采样频率是不同的。对于电压ADC采样频率是开关频率的两倍，如图8所示。采样时刻都是在导通时间段和关断时间段的中点。在这阶段，假设模数转换时间和计算时间足够短，以至于采样电压在时刻nTs时，占空比会在紧接着的关断边缘更新。因此，称这个延时为tdv1。同样，当采样时刻为(n+1)Ts，延时为tdv2。对小信号回路的分析，考虑这两种延时的最坏情况。如

图8 电压模数检测延时Fig.8 Voltage A-D sensing delay

对于电流ADC采样频率等于开关频率。采样时刻在每个开关关断时间段的中点，如图9所示。

图9 电流模数检测延时Fig.9 Current A-D sensing delay

与电压ADC推导的方法类似，电流回路的延时时间计算如下

ADC包括一个数字转换器。数字转换器是一个非线性的模块，它有非线性的增益。当扰动足够大（相比于转换器的阶梯波幅值）时，非线性增益可简化为线性的。故做出如下假设，数字转换器的增益为一线性值，即

式中，QAD是转换器的阶梯波幅值。

对于电压ADC，这个值通常是固定不变的。对于电流ADC，情况则有所不同。因为数控芯片内部会将检测到的电流值重新转换成它的真实值。例如，电感电流值是10A，考虑到检测和采样的增益，用于计算的电流信息设定为10A。在这情况下，电流ADC的整体增益就可以设定为1。

3.3 纹波滤波器小信号建模的建立

对于电压回路，采样频率是开关频率的两倍。因此，采样电压仍会有开关频率部分的噪声，这是回路补偿所不希望的。抗混滤波器是一阶低通滤波器，其截止频率大概在1MHz范围，所以它不能消除开关频率附近的纹波。为解决这个问题，引入了一个数字滤波器。

此滤波器的Z域传递函数如下

此滤波器的物理意义是将连续的两个采样值取平均。为得到它的等效S域传递函数，在此采用双

其Z域和S域传递函数的伯德图如图10所示。

电流回路中电流纹波滤波器与其类似，这里不再赘述。

图10 纹波滤波器Z域和S域伯德图的比较Fig.10 Comparison of Bode plot of Z-domain andS-domain ripple filter

3.4 数字补偿器小信号模型的建立

数字控制回路使用比例、积分、微分（PID）补偿器来修正检测的数字化电压使其稳定在给定值。额外的二阶微分增益和二阶后置滤波器提供高阶零、极点，进一步优化回路宽范围的性能。所有回路参数在一定的范围内是可编程的，允许的回路带宽是10～300kHz，同时它也取决于主功率电路的形式。式（13）给出了一个通用的补偿器的表达式。

式中，Ki、Kp、Kd和Kd2分别是积分、比例、微分和二阶微分增益；Kfd1、Kfd2是二阶全极点低通后置滤波器的系数。

采用双线性变换，等效的S域传递函数可推导如下

从式（14）可以看出，补偿器实际上是一个三极点、三零点的补偿器。

3.5 DPWM小信号模型的建立

控制电路中采用双沿数字调制波。在小信号的分析，忽视非线性增益，将其视作为一个线性增益。图11是DPWM的增益推导。

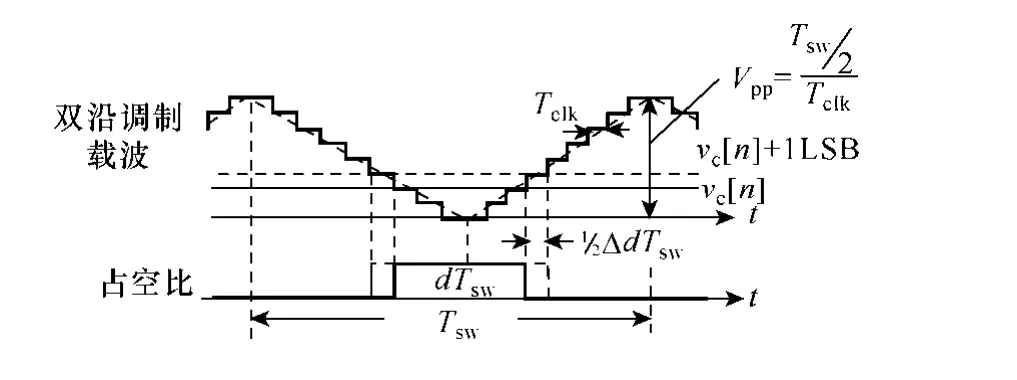
图11 DPWM的增益推导Fig.11 Derivation of DPWM gain

与模拟的PWM推导类似，DPWM的增益如下

式中，Tsw是开关周期；Tclk是DPWM的分辨。

3.6 数字控制器完整小信号模型的建立

以上将数字控制电路各组成部分分别建模，依此图12给出了完整数字控制器小信号模型。

图12 数字控制12V自驱VRM的小信号模型Fig.12 Small signal model of digitally controlled 12Vself-driven VRM

电流回路的增益是

电压回路的增益（电流回路开路）是

整个电压回路的增益T2（电流回路闭合）是

4 自适应电压定位设计方法

对于AVP回路的设计，借鉴了文献[18]提出的恒定输出阻抗设计概念。高带宽的电流回路设计可将一个二阶系统简化成一阶系统。当电流回路闭合及电压回路开路时，变换器可当成一个理想的电流源，它的输出阻抗近似表示如下

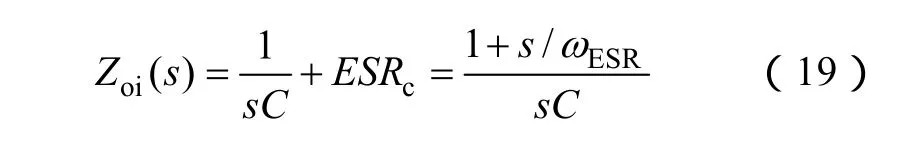
图13是电流回路闭合时的电路图，变换器因而简化成一个一阶系统。电流源的阻抗无穷大，故只有输出电容会影响到系统的输出阻抗。

图13 电流回路闭合12V自驱VRM电路图Fig.13 Circuit diagram of 12V self-driven VRM withcurrent loop closed

图14是恒定输出阻抗设计示意图。为了实现恒定的输出阻抗，系统回路 T2应设计成斜率为-20dB/dec，截止频率ωc由Rdroop值和全部的输出电容决定。期望的T2是

式（18）已经给出T2的表达式，将已知的表达式代入，联立式（18）和式（20），可以得到补偿器的确切表达式，并依此设计补偿电路。一般的补偿电路，只需要双极点和单零点，形如

其中，积分环节是用来消除稳态误差；零点是用来补偿系统的双极点；高频域范围的极点是用来进一步衰减开关噪声的，但也可省略以简化补偿器的设计。设计K值，从而得到电流回路的高带宽ωci。

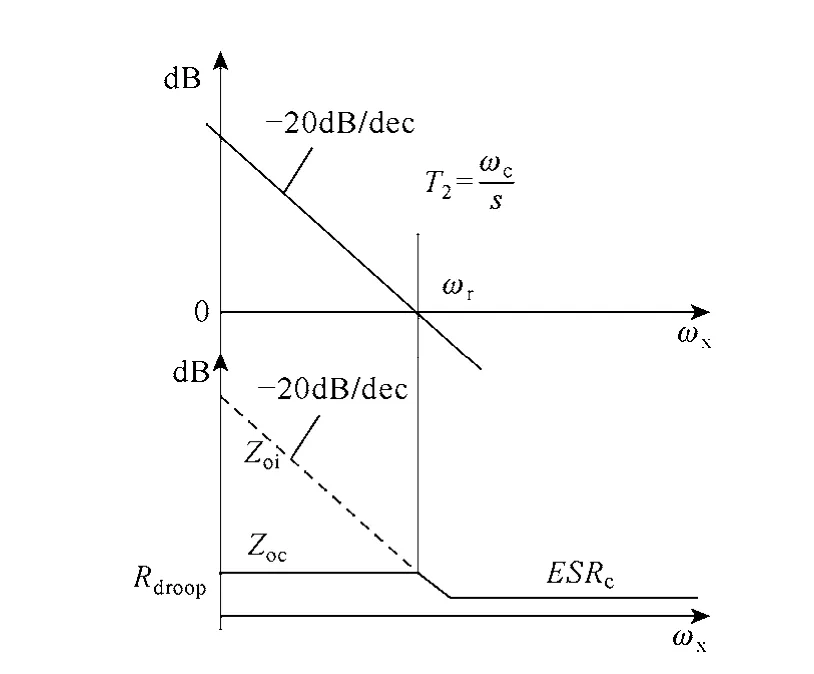
图14 恒定输出阻抗设计Fig.14 Constant output impedance design

5 仿真和实验结果

图15 自适应电压定位12V自驱VRM仿真结果Fig.15 Simulation results of 12V self-driven VRM with AVP

为验证模型和设计策略，搭建了SIMPLIS仿真电路。图15是T2的回路增益和闭合回路输出阻抗的仿真模型。T2的带宽是110kHz，相位裕度是70°，高于带宽时输出阻抗是恒定的。图16是负载跳变（Io:0A→100A→0A）时域的仿真结果。

图16 12V自驱VRM负载跳变的仿真结果Fig.16 Simulation results of 12V self-driven VRMof load transient

为了验证理论分析的正确性，在实验室制作了一台实验样机，主功率电路的参数如表1所示。图17是1UVRM样机的图片。图18是实验结果，控制带宽是106kHz，相位裕度65°。图19是负载跳变时实验结果的时域波形。实验结果表明，根据本文所提出的小信号模型，设计的电路控制参数可以满足要求，实验结果验证了理论分析的正确性。这里输出滤波电容的取值（2mF）较理论计算（1mF左右）的大。因为控制器的延时效应产生较大的电压波动，而VRM对电压的要求又很严格，没有其他更好的方法消除，故只能增大输出滤波电容。

表 主功率电路参数Tab. Parameters of main circuit

图17 原理样机Fig.17 The prototype picture图18

图18 2mF电容的回路测量结果Fig.18 Loop measurement with 2mF capacitor

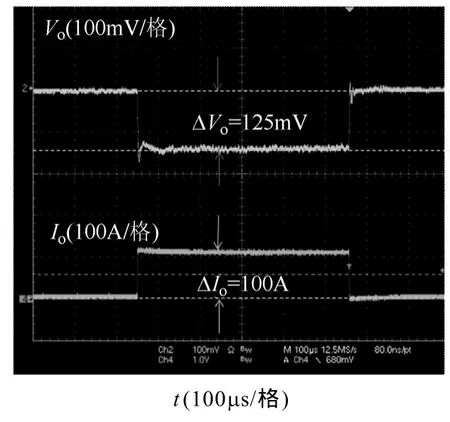
图19 2mF电容的动态性能Fig.19 Load dynamics with 2mF capacitor

6 结论

本文提出了一种系统的数字控制VRM建模方法。对12VZVS自驱VRM的主电路和控制电路逐一进行建模，最后给出了完整模型。通过这种方法，可以更直观地了解数字控制器。在此基础上设计控制器并实现了AVP功能。这种方法准确、直观。最后通过仿真及实验结果很好地验证了理论分析的正确性。

[1] Voltage regulator module(VRM) and enterprise voltageregulator-down(EVRD) 11.0 design guidelines[S].Santa Clara, CA: Intel Crop., 2006.

[2] Zhou X, Zhang X, Liu J. Investigation of candidate VRM topologies for future microprocessors[C]. Proceedingsof the IEEE APEC, 1998: 145-150.

[3] Yao K, Xu M, Meng Y, et al. Design considerationsfor VRM transient response based on the output impedance[J]. IEEE Transactions on Power Electronics,2003, 18(6): 1270-1277.

[4] Ren Y, Yao K, Xu M, et al. Analysis of the powerdelivery path from 12V VR to the microprocessor[J].IEEE Transactions on Power Electronics, 2004, 19(6):1507-1514.

[5] Zhang Z, Eberle W, Yang Z, et al. Optimal design ofresonant gate driver for buck converter based on anew analytical loss model[J]. IEEE Transactions onPower Electronics, 2008, 23(2): 653-666.

[6] Zhou J, Xu M, Sun J, et al. A self-driven softswitchingvoltage regulator for future microprocessors[J]. IEEE Transactions on Power Electronics,2005, 20(4): 806-814.

[7] Alou P, Cobos J A, Garcia O. A new driving schemefor synchronous rectifiers: Single winding self-drivensynchronous rectification[J]. IEEE Transactions onPower Electronics, 2001, 16(6): 803-811.

[8] Ren Y, Xu M, Sterk D, et al. 1 MHz self-driven ZVSfull-bridge converter for 48 V power pods[C]. PowerElectronics Specialist Conference, 2003: 1801-1806.

[9] 甘鸿坚，严仰光.高频PWM 直-直变换的同步整流技术[J].电力电子技术,1998,32(4):105-108.Gan Hongjian, Yan Yangguang. Synchronous rectifierof high frequency DC-DC converters[J]. PowerElectronics, 1998, 32(4): 105-108.

[10]谢小高,张军明,钱照明.基于新型同步整流驱动方案的绿色电源[J].电工技术学报，2007，22(3)：96-101.Xie Xiaogao, Zhang Junming, Qian Zhaoming. Agreen power supply based on a new synchronousrectification[J]. Transactions of China ElectrotechnicalSociety, 2007, 22(3): 96-101.

[11]钱照明，何湘宁.电力电子技术及其应用的最新发展(一)[J].中国电机工程学报,1997,17(6):361-366.Qian Zhaoming, He Xiangning. The recent developmentsof power electronics and its applications(1)[J].Proceedings of the CSEE, 1997, 17(6): 361-366.

[12]钱照明，董伯藩，何湘宁.电力电子技术及其应用的最新发展(二)[J].中国电机工程学报,1998,18(3):153-162.Qian Zhaoming， Dong Bofan， He Xiangning. Therecent developments of power electronics and itsapplications(II)[J]. Proceedings of the CSEE, 1998,18(3): 153-162.

[13]Van de Sype D M, De Gussems K, Van den BosscheA P. Experimental verification of the Z-domain modelfor digitally controlled converters[C]. Power ElectronicsSpecialists Conference, 2005: 2164-2170.

[14]Maksimovic D, Zane R. Small-signal discrete-timemodeling of digitally controlled PWM converters [J].IEEE Transactions on Power Electronics, 2007, 22(6):2552-2556.

[15]Maksimovic D, Zane R, Erickson R. Impact of digitalcontrol in power electronics[C]. Proceedings of ISPSD2004: 13-22.

[16]Corradini L, Mattavelli P. Analysis of multiplesampling technique for digitally controlled DC-DCconverters[C]. Power Electronics Specialists Conference,2006: 1-6.

[17]Corradini L, Mattavelli P. Modeling of multisampledpulse width modulators for digitally controlled DCDCconverters[J]. IEEE Transactions on PowerElectronics, 2008, 23(4): 1839-1847.

[18]Yao K, Meng Y, Xu P, et al. Design considerationsfor VRM transient response based on the outputimpedance[J]. IEEE Transactions on Power Electronics,2003, 18(6): 1270-1277.