基于免疫算法的逆变器多目标Pareto最优控制策略
2014-11-15袁佳歆费雯丽陈耀军陈柏超潘建斌饶斌斌
袁佳歆 赵 震 费雯丽 陈耀军 陈柏超 潘建斌 饶斌斌
(1. 武汉大学电气工程学院 武汉 430072 2. 江西省电力科学研究院 南昌 330006)
1 引言
随着能源结构的调整与电力需求快速增长,为了能够高效地使用电能,大量需要能将电压和频率变换的系统[1,2]。逆变器可以满足电能变换的要求,因此备受关注。研究逆变器的主要目标有提高输出波形质量(减小总谐波畸变率),降低电力电子开关损耗,延长器件寿命,减小逆变器装置体积等。其中两个研究热点是提高逆变器输出波形质量和降低逆变器损耗[3-5]。但一般来说这两个目标是矛盾的。例如通过提高器件的开关频率来改善逆变器的输出波形质量时,就会导致损耗增加。如何在这两个目标之间进行权衡是逆变器优化控制研究的难点。
现有针对逆变器输出波形质量及损耗研究的本质是使一个性能指标满足一定约束条件下,优化另一目标[3-5],从而实现将多目标问题转化成单目标问题。该类方法需要研究约束条件的选择性问题和适应性问题。文献[3]提出最小开关损耗空间矢量脉宽调制控制技术,在满足空间矢量控制的条件下优化矢量及顺序使开关损耗减小。其中采用空间矢量控制策略的实质是使输出波形质量满足一定范围。文献[4]采用特定谐波消除脉宽调制技术,使得电力电子器件在开关次数和损耗一定的范围内,提高逆变器输出波形质量。还有学者采用软开关技术来减小开关损耗[5],使器件在零电压条件下开断,消除开关损耗和噪声,但仍存在成本高,结构复杂等不足。
文献[6]利用采取权重系数法求逆变器多目标(波形质量和开关损耗)最优控制序列。其中选择权重系数是难点,需要大量的先验知识,并且该文献只是对损耗进行定性分析,没有定量计算。文献[7]采用免疫算法(Immune Algorithm, IA)用于三相逆变器控制最优控制中,克服GA的收敛速度较慢和局部搜索能力不足等问题,没有考虑多目标问题。
多目标优化问题通常具有多个Pareto非劣解[8,9],基于Pareto最优的多目标优化方法目的在于搜索尽可能完整和分布均匀的Pareto非劣解集作为决策方案集,进而从中根据一定的原则和偏好进行决策。文献[8]基于快速非支配排序遗传算法求取多目标无功优化中的Pareto最优解。文献[9]通过改进的强度Pareto进化算法实现对多目标电网规划。
本文在这些工作基础上,建立了器件的精确损耗计算模型,提出了一种基于 IA的逆变器多目标Pareto最优解集方法,即波形质量与损耗两个目标。并进一步研究不同条件下的多目标 Pareto最优解集,使用户能够根据实际需要进行选择。
2 逆变器多目标优化模型
2.1 逆变器矢量控制
图 1所示为电压型单相逆变器等效拓扑电路图。
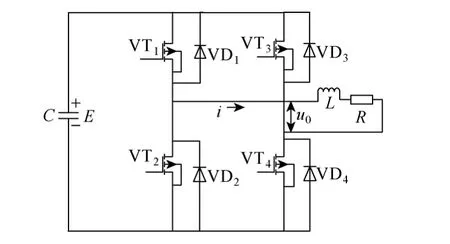
图1 单相逆变器主电路图Fig.1 Signal-phase full-bridge inverter
图中,VT1~VT4为全控型开关,V=1时表示导通;反之,V=0代表关断,VD1~VD4为反并联二极管,逆变器输出电压为u0,L为电感,R为电阻。当开关VT1、VT4导通,且VT2、VT3关断时,逆变器输出电压为 u0=E;当开关VT1、VT4关断,且VT2、VT3导通时,逆变器输出电压为 u0=-E。定义每个时刻工作状态变量Xm为

在一个工频周期内,不同时刻 VT1~VT4的工作状态变量Xm构成一个空间矢量xi=(X1,X2,…,Xn),其中n为矢量长度。
2.2 计算逆变器输出波形
本文采用分段函数描述逆变器输出电流值,第m个时间段内的输出电流函数为

结合式(1)及式(2)可以看出,一个周期内各个时刻的Sm取值由空间矢量xi=(X1, X2,…, Xn)的矢量序列决定,因而对于不同的矢量序列,一个周期内各个时刻的输出电流Im(t)也会不同。

参考标准电流正弦函数为式中,参考标准电流的幅值A由直流侧电压E、逆变器调制比m以及负载值决定。
2.3 计算逆变器损耗
电力电子器件的损耗计算模型是研究降低损耗的关键。文献[10]通过分析逆变器开关损耗过程,建立逆变器损耗的数学模型,但由于逆变器工作的环境是动态的,其模型建立比较复杂且存在一定的相对性。文献[11]通过建立转换器功率器件模块的 3D热模型,进行热模拟分析来估算损耗,其温度模型的建立较为复杂。文献[12]提出利用厂商给出的器件数据电子手册,通过曲线拟合方式获取损耗模型估算损耗,方法简单易实现。本文结合自身的逆变器模型,采用文献[12]中的逆变器损耗计算方法。
逆变器损耗主要包括:功率器件开关损耗,通态损耗和截止损耗。绝缘栅双极晶体管(IGBT)的正向截止损耗和驱动损耗在总损耗中占的比例较少,忽略不计。故将其具体分为:全控型开关开通损耗Pson,全控型开关关断损耗Psoff,反并联二极管关断损耗Pdoff,全控型开关通态损耗Pscond,反并联二极管通态损耗Pdcond。本文以图1中的一个开关单位(VT1、VD1)为研究对象,根据开关门极信号和电流方向作为损耗增加部分的依据。表1所示为逆变器在不同状态条件下VT1和VD1所对应的工作状态。得逆变器中各部分的损耗表达式为

图2 计算损耗流程图Fig.2 Flow chart of calculating switching losses

表1 不同电流和信号条件下的开关动作情况Tab.1 The status of switch and diode in different conditions
在一个周期内通过获得电流和门极信号,参照表1可以得到一个周期逆变器中各部分损耗和总损耗,图2所示为计算损耗的流程图。
本文利用厂家提供的电子数据手册 Datasheet中的相关资料,获取 Vd=f(Ice),Vceo= f(Ice),Pdoff/Pson/Psoff= f(Ice)等相关曲线。由于厂商给出的数据一般考虑了开关自身的特性,且包括在不同电流、不同负载及不同节点温度做的实验,其结果相对也较为精确。于是从图形中采集曲线5~6个点,通过Matlab中Polyfit函数进行曲线拟合得出多项式参数,其中由于一般厂商提供的数据都是在额定电压下,比对实际情况需要将电压做相应的调整换算,即可以获

流母线电压UDC有关,m表示某一时刻状态。
通过式(4)~式(8)即可以得出某一时刻的总损耗为

若P(m)值越小,说明逆变器产生的损耗越小。
3 基于免疫算法的多目标优化
3.1 Pareto最优解
针对一般多目标的极大值问题max(f(x), g(x)),Pareto解是建立在集合论上对多目标解的一种评估方式。Pareto解的定义为:在设计变量的取值范围内,对于设计变量x*,当且仅当不存在其他变量x,满足 f(x)≥f(x*)且 g(x)≥g(x*),则 x*为其中一个最优解。对多目标优化问题而言,其Pareto最优解不是唯一,而是一个集合,且此解集构成优化的Pareto前沿面。在可行解集中没有比Pareto最优解所对应的个体绝对占优。由于Pareto最优解集中的任何解都可能成为最优解,因而设计者可以根据意愿和对各目标的重视程度,从Pareto最优解集中选择出最满意的解。本文中,即是应用所提出的方法可求取逆变器输出波形质量及逆变器损耗的Pareto最优解集,用户根据实际要求选择其中需要的解,实际控制时只需要通过查表来获得解集,不需要在线计算。
3.2 免疫算法
IA是在遗传算法基础上的模拟生物抗体浓度自适应调节过程的一种全局优化算法。它借鉴生物学中免疫系统识别外来物的刺激,并能对之做出准确的应答。IA的主要特点有:具有免疫记忆功能,能加快搜索速度,确保目标函数快速收敛;具有浓度计算操作能够保证抗体种群的多样性。本文所采用免疫算法流程如图3所示,其中整体亲和度计算模型的建立是求取Pareto最优解集方法的关键,下文将会具体分析,而编码操作、注射疫苗、计算浓度、免疫选择、交叉操作、倒位操作、添加操作,形成新一代个体均与文献[7]相似,此处不再赘述。
3.3 多目标免疫算法流程
本文由于需要综合考虑输出波形质量与开关损耗,假设某个抗体 xi=(X1,X2,…,Xn),逆变器输出波形质量评价函数用逆变器输出电流与参考标准正弦电流差的平方和的倒数表示。即

逆变器损耗是一个累加函数,抗体xi的损耗为

式中,n代表基因总长度。
抗体xi损耗评价函数用其损耗的倒数表示。

图3 IA流程图Fig.3 Flow chart of the IA

则本文的整体亲和度表达式为

式中,f(xi)为波形质量评价函数,g(xi)为损耗评价函数,其值由抗体xi的矢量序列决定。目标函数即为整体亲和度函数 Fitness(xi),要求取相应的抗体xi使其Fitness(xi)最大。WQ为每次迭代运算中给定的波形质量评价函数参考值,Kstep为迭代运算中波形质量 WQ增加的步长,本文取 Kstep=100。k1为一个常系数,为增大 g(xi)的影响力,k1设置为一个k1g(xi)>>f(xi)的值,本文取k1=100 000。
式(13)及k1参数设置表明,对于每次迭代运算给定的WQ值,IA寻优得到的是波形质量(WQ,WQ+Kstep)范围内,逆变器损耗评价函数 g(xi)为最大值的抗体,设此时对应的抗体为x1。可以看出,在波形质量的取值范围(WQ,WQ+Kstep)内,对于抗体 x1,不存在其他任何抗体 x,同时满足 f(x)≥f(x1)且 g(x)≥g(x1),故抗体 x1一定为波形质量范围(WQ,WQ+Kstep)中一个Pareto最优解。而对于波形质量(WQ,WQ+Kstep)范围外的抗体,其整体亲和度较小,相当于对该类抗体进行了惩罚,这样有利于引导算法的搜索空间朝波形质量在(WQ,WQ+Kstep)范围内,开关损耗较小的区域逼近。
进一步考虑到,在实际应用中,为保证输入系统的谐波不能太大以及逆变器输出波形的能力限制,逆变器的波形质量应该存在一定的允许范围(WQmin,WQmax)。因而要求逆变器输出波形质量与损耗的Pareto最优解,只需要求波形质量(WQmin,WQmax)范围内的Pareto最优解。本文中,由滞环控制下逆变器输出波形质量确定波形质量最小值WQmin,由不考虑损耗情况下的IA优化的最优波形质量确定波形质量最大值 WQmax。设通过步长 Kstep将该波形质量划分为p个区域,以步长Kstep逐渐增加WQ值,经过IA算法寻优即可求取各波形质量范围内的p个解。将这p个解的波形质量评价函数值f(xi)及损耗评价函数值g(xi)进行比较,即可筛选得到全局范围的Pareto最优解集。
根据实际电路条件的不同,如逆变器调制比、负载的不同,每次所得出的最优解集也是不同的,但都可以通过本文所提出的方法求得当前电路条件下的Pareto最优解集,供用户根据实际要求选择最适宜的解。仿真及实验部分将在几组不同负载条件下对本文所提出的方法加以验证。
4 仿真
4.1 仿真参数设置
本文以图1为仿真主电路,其参数设置如下:频率f=50Hz,电压调制比m=0.85,开关频率为20 kHz,直流测电压E=88 V,滞环环宽H=3%。免疫算法参数中种群为 200,染色体长度 200,交叉率Pc=0.55,变异率Pm=0.006,倒位率Pcon=0.005,权重系数参数 a=b=0.5。在仿真中以纯电感负载和几组阻感性负载为例,对本文提出的求取逆变器损耗与波形质量的Pareto最优解集的方法加以验证。
4.2 纯电感负载
图4所示的是在纯电感负载(L=28mH)条件下,逆变器Pareto最优解集中,波形质量最优及损耗最优两种情况下,逆变器的空间矢量序列、相应的 PWM控制信号及输出波形。其对应波形质量评价函数分别为1 600、600;损耗评价函数分别为16.468 644、21.382 318。从输出波形质量上来讲,图 4c明显要优于图 4f波形。将其输出电流进行傅里叶分解,在此两种不同的PWM控制策略下THD分别为 1.4%与 3.15%,最优波形 THD降低了55.56%。


图4 不同控制条件下逆变器矢量序列及输出波形Fig.4 The sequence and output waveforms of inverter in different control strategies
但是从电压的输出波形图中明显可以看出,THD较小时开关动作次数要多于较大时,且各开关开断间隔时间不等,特别是在电流比较大的时候动作次数明显增多。在此两种控制策略下,逆变器损耗总值分别为 0.060 722和 0.046 768,损耗增加了29.837%。
图5所示为在波形质量评价函数取值范围内,各波形质量评价函数值与对应的输出波形 THD关系图,波形质量评价函数值越大其对应的 THD越小,反之,THD越大。所以波形质量评价函数可以间接反映THD。

图5 THD与波形质量评价函数之间的关系Fig.5 The relationship between THD and waveform quality
图6所示曲线为IA算法计算开关损耗与THD之间的Pareto前沿面,其中,拟合曲线的曲线拟合函数为。上三角区域为可行解区域。随着THD增大,波形质量的降低,逆变器的损耗在逐渐降低。

图6 开关损耗与THD之间的关系Fig.6 The relationship between switching losses and THD
4.3 阻感性负载
设定负载总阻抗Z不变,根据电阻R所占总阻抗Z的比例不同,负载参数设置见表2。

表2 负载参数Tab.2 The parameters of the load
图7所示为表2所设负载参数条件下,损耗评价函数与波形质量评价函数之间的Pareto前沿面。

图7 在不同负载条件下损耗评价函数与波形质量评价函数之间的关系Fig.7 The relationship between switching losses and waveform quality in different loads
由图7所示可知,在不同负载条件下多目标IA算法可以得出 Pareto最优解集。由于负载不同 IA优化所得控制序列不同,所得损耗也随之变化。从上述仿真图形可以看出,在不同负载条件下,均可通过本文所述的方法求取逆变器开关损耗与输出波形质量的Pareto最优解集。
此外,通过不同负载下的仿真研究表明,由于波形质量与逆变器损耗是对相对矛盾的量,当波形质量函数值逐渐增大,损耗评价函数值是逐渐减小的,因而在各个波形质量(WQ,WQ+Kstep)范围内,所求得的损耗评价函数最大的抗体均为全局范围内的Pareto最优解。为了更加精确地描绘出Pareto前沿面,也可以减小步长Kstep的设置,获得Pareto前沿面中较多的解。
5 实验
5.1 实验平台
本文设计如图8a所示的实验平台,由以下几部分组成:①由 DSP2812和 FPGA EP2C20Q240-C8芯片组成的控制中央处理系统。其中 DSP负责采集、计算和人机交互等功能,FPGA负责产生多路高速数字 PWM控制信号。②驱动放大、保护单元中央处理系统得到控制信号,通过基于EXB841的IGBT驱动、保护和脉冲放大电路驱动逆变器主电路。③主电路是由4个BSM100GB60DLC型IGBT和 RCD吸收缓冲回路组成的单相全桥逆变器,其中,BSM100GB60DLC的热阻值为0.07。

图8 实验原理图Fig.8 Schematic diagram of experiment
5.2 测量损耗实验
为了对逆变器开关损耗的数学模型进行验证,本文设计如图8b所示的损耗测试电路。该电路由热敏电阻 PT100,放大器INA128(本文放大501倍)和可调电阻R组成的惠斯登电桥组成。在不同PWM开关控制序列控制逆变器的条件下,逆变器的每周期总能量损耗是不同的,热敏电阻的阻值也不同。通过惠斯登电桥测量出的电压间接计算出PT100的阻值,本文在测量首先需要调节R3使得初始输出电压为0,此时假设R3+R4=R5,PT100阻值为R6,输出电压为U0,α=501,则阻值换算表达式为

已知R1=R2=10kΩ、R4=100Ω,由式(14)即可算出R6,查询对应阻值与温度数据表即可以得出其对应的温度值。由温度差值及 IGBT的热阻值即可计算出IGBT的损耗。
5.3 实验结果与分析
实验在纯电感负载、调制比为0.85的情况下对相应的仿真结果进行了验证,其参数设置与仿真电路参数相同。
图9a为波形质量最优情况下的输出波形,其中1号曲线为逆变器电压波形,2号曲线是电流波形,此时波形质量评价函数 WQ设为 1 600。图 9b为损耗最优情况下的输出波形,此时波形质量评价函数WQ设为600。图9a的输出波形明显优于图9b的输出波形。将实验结果导入Matlab 进行 FFT分析,其THD分别为1.46%和3.23%。

图9 不同控制条件下逆变器输出波形Fig.9 The output waveforms of the inverter in different control strategies
同样地,通过实验可以获取在不同波形质量条件下逆变器的输出波形THD及损耗值。表3所示即为当逆变器波形质量评价函数WQ从600到1 600变化时所测得的实验数据,测量时间为3min。
利用PT100热测量方式测量损耗,由于示波器探头精度影响、PT100测量回路很难完全调整到电桥完全平衡、读取PT100电阻对应温度时存在一定的估读,因而会带来一定的误差,但表3数据表明,实际实验测量结果与理论计算结果误差最大不超过10%,因而该损耗计算方法是可行的。另外,由于仿真中的逆变器开关器件都是理想器件,而实际试验中逆变器的开关器件有开通、关断延时以及一定的导通压降,因而会在一定程度上影响输出波形质量,使得逆变器输出波形THD在仿真值与实验值上有一定的误差,但从实验数据可以看出,该误差最大值小于5%。
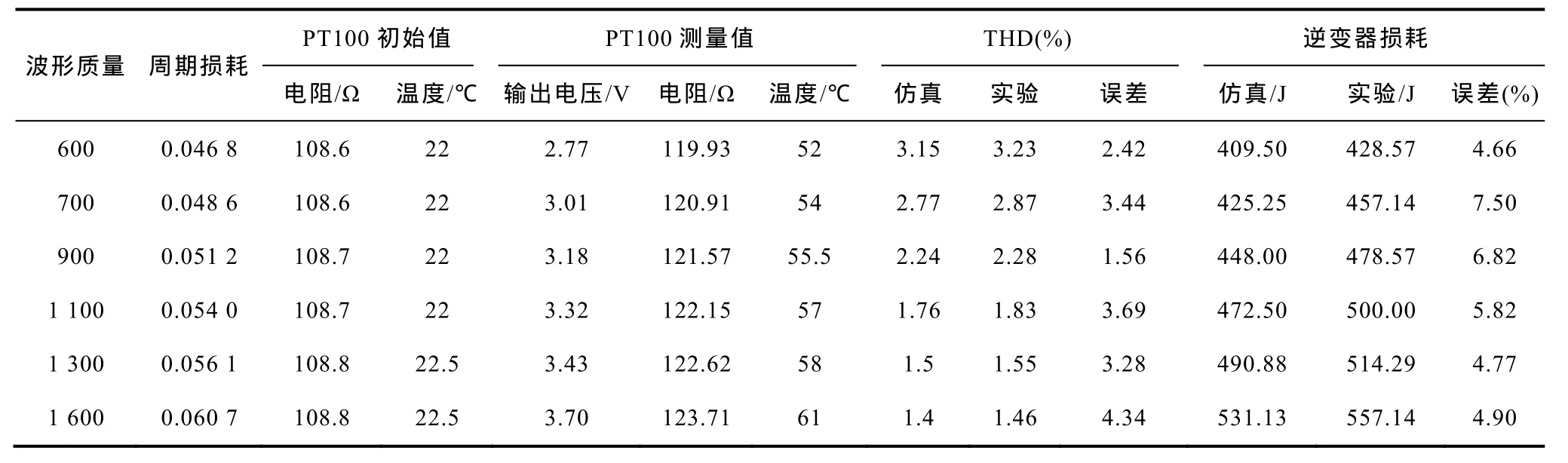
表3 不同控制策略下逆变器输出结果Tab.3 Output of inverter control by different control strategies
从表3的波形质量评价函数、THD及逆变器损耗三项数据可以看出,利用提高逆变器输出波形质量的同时逆变器的损耗增加。因而在实验中,实验设计者可以根据意愿和对各目标的重视程度,从中选择出最满意的实验条件进行实验研究。
6 结论
本文提出基于 IA寻求逆变器多目标最优解集的方法,与其他方法相比具有以下优势:
(1)免疫算法适合于求取逆变器的数字化多目标PWM控制;将逆变器的数字化PWM控制序列转化为N维空间的解,在不同负载、调制比条件下,均可利用 IA在解空间中寻找到多目标 Pareto最优解集,这样有利于供设计者按设计意愿选择最优的设计方案。仿真与实验验证了该方法的可行性。
(2)本文采取的损耗估算方法相对简单且准确度好。仿真和实验验证了该方法的有效性和准确性。该方法能够有效利用厂家提供的器件特性参数,具有可操作性,适合于实际工程应用。
[1] Loh P C, Li Ding, Chai Yikang, et al. Hybrid AC–DC microgrids with energy storages and progressive energy flow tuning[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1533-1543.
[2] Pan C T, Cheng M C, Lai C M. A novel integrated DC/AC converter with high voltage gain capability for distributed energy resource systems[J]. IEEE Transactions on Power Electronics, 2012, 27(5):2385-2395.
[3] 倪喜军, 赵剑锋, 曹武, 等. 开关损耗优化的级联型逆变器全区域空间矢量调制策略[J]. 电工技术学报, 2012, 27(4): 101-109.Ni Xijun, Zhao Jianfeng, Cao Wu, et al. Switching loss optimized svpwm algorithm for cascade multilevel inverters in all region[J]. Transactions of China Electrotechnical Society, 2012, 27(4): 101-109.
[4] Zhao Z M, Zhong Y L, Gao H W, et al. Hybrid selective harmonic elimination PWM for commonmode voltage reduction in three-level neutral-pointclamped inverters for variable speed induction drives[J]. IEEE Transactions on Power Electronics,2012, 27(3): 1152-1158.
[5] Amini M R, Mahdavi M, Emrani A, et al. Soft switching bridgeless power factor correction with reduced conduction losses and no stresses[J]. IET Power Electronics, 2012, 5(3): 334-340.
[6] 袁佳歆, 陈柏超, 贾嘉斌. 基于遗传算法的逆变器控制规律[J]. 电力系统自动化, 2004, 28(24): 32-35.Yuan Jiaxin, Chen Baichao, Jia Jiabin. Genetic algorithm based approach for inverter control[J].Automation of Electric Power Systems, 2004, 18(24):32-35.
[7] Yuan J X, Pan J B, Fei W L, et al. An immune algorithm based space-vector PWM control strategy in a three-phase inverter[J]. IEEE Transactions on Industrial Electronics, 2013, 60(5): 2084-2093.
[8] 冯士刚, 艾芊. 带精英策略的快速非支配排序遗传算法在多目标无功优化中的应用[J]. 电工技术学报,2007, 22(12): 146-151.Feng Shigang, Ai Qian. Application of fast and elitist non-dominated sorting generic algorithm in multiobjective reactive power optimization[J]. Transactions of China Electrotechnical Society, 2007, 22(12):146-151.
[9] 王一, 程浩忠. 计及输电阻塞的帕累托最优多目标电网规划[J]. 中国电机工程学报, 2008, 28(13):132-138.Wang Yi, Cheng Haozhong. Pareto optimality based multi-objective transmission planning considering transmission congestion[J]. Proceedings of the CSEE,2008, 28(13): 132-138.
[10] 洪峰, 单任仲, 王慧贞, 等. 一种逆变器损耗分析与计算的新方法[J]. 中国电机工程学报, 2008,28(15): 72-78.Hong Feng, Shan Renzhong, Wang Huizhen, et al.Analysis and calculation of inverter power loss[J].Proceedings of the CSEE, 2008, 28(15): 72-78.
[11] Swan I, Bryant A, Mawby P A, et al. A fast loss and temperature simulation method for power converters,part II: 3-D thermal model of power module[J]. IEEE Transactions on Power Electronics, 2012, 27(1):285-288.
[12] Bazzi A M, Krein P T, Kimball J W. IGBT and diode loss estimation under hysteresis switching[J]. IEEE Transactions on Power Electronics, 2012, 27(3):1044-1048.
