基于时频相似度的油纸绝缘多局部放电源脉冲群分离与识别策略

汪 可 李金忠 张书琦 廖瑞金 朱 洁 伍飞飞

（1. 中国电力科学研究院 北京 100192 2. 重庆大学输配电装备及系统安全与新技术国家重点实验室 重庆 400044 3. 国网技术学院 泰安 271000）

1 引言

变压器是电网中的核心设备，其安全运行直接决定了电能供应的可靠性[1]。在设备制造、运输以及长期运行过程中会不可避免地产生绝缘缺陷并引发的局部放电（Partial Discharge, PD），严重影响变压器的可靠运行。因此，局部放电源的分析与诊断一直是变压器状态评估的重要内容，能够为制定合理的变压器维护与检修策略提供参考依据。

随着数字信号处理与人工智能技术的飞速发展，国内外对局部放电缺陷类型识别开展了大量的研究工作[2-6]。大部分工作是通过实验室采集单一人工缺陷模型的局部放电信号构造特征数据库，设计合理的分类器对采集的局部放电样本进行识别。其中，以局部放电相位分布的（Phase-Resolved Partial Discharge，PRPD）统计特征应用最为广泛。变压器油纸绝缘为液-固两相复合绝缘，随着运行年限的增加，加上复杂的内部结构，往往同时在多处出现局部放电。并且，恶劣的运行环境也有可能造成外套管表面发生局部放电。因此，由变压器局部放电监测装置得到的信号往往是多处放电源脉冲的叠加，相应的PRPD图谱会出现部分或完全的交叉、重叠，导致识别错误。由此可知，传统单一缺陷的 PRPD特征数据库无法对多局部放电源信号进行识别。

为了解决这一难题，近年来国内学者对多放电源的诊断进行了一定的探索，认为传感器接收到来自于同一局部放电源的脉冲具有某种类似的特性，而不同局部放电源的脉冲具有相互区分的特征[7]。一个PD脉冲的持续时间通常为几百ns到几μs，在这个时间内发生两次及以上放电的概率极小。假设在一个 PD脉冲持续时间内不会发生两次及以上的放电，那么在记录每个PD脉冲幅值和相位的同时，保存对应的放电脉冲波形，通过提取单个 PD脉冲具有强鉴别力的特征，使来自于不同局部放电源的脉冲最大区分，同一局部放电源的脉冲最大聚集，采用聚类方法即可实现多局部放电源脉冲群的分离，再结合单一缺陷的放电指纹，即可对多放电源进行识别。具有代表性的是G. C. Montanari等人提出的等效时频分析（Equivalent Time-Frequency Analysis,ETFA）方法，通过计算局部放电脉冲的等效时宽T与等效频宽F两个参数，将单个局部放电脉冲映射到时频T-F平面上。研究结果表明，来自不同缺陷的局部放电信号能够在T-F平面上抱团，有效实现放电源信号的分离[8-10]。另外，自相关函数（Autocorrelation Function, ACF）[7,11]、幅值-频率空间（Amplitude-Frequency Space, AFS）[12]、小波分解（Wavelet Decomposition, WD）结合主成分分析（Principal Component Analysis, PCA）[13]、包络线比较（Envelope Comparison, EC）[14]、盲源分离（Blind Source Separation, BSS）[15]以及基于多通道同步检测的三相幅值关联分析（3-Phase Amplitude Relation Diagram, 3PARD）[16-18]等方法先后被提出用于分离多局部放电源脉冲群。

ETFA等方法的研究结果表明，对局部放电脉冲提取特征并进行聚类来分离多局部放电源脉冲群的思路是可行的。本文基于相同的局部放电脉冲群可分假设，提出一种基于时频分析（Time-Frequency Analysis, TFA）结合近邻传播聚类（Affinity Propagation Clustering, APC）的多局部放电源识别新方法，整个算法流程如图1所示。在脉冲群分离部分，首先从采集的多局部放电源原始数据中提取单个PD脉冲波形，同时保存每个PD脉冲的相位-幅值数据；然后，对单个PD脉冲进行S变换（S Transform, ST）并保存其对应的ST幅值（ST Amplitude, STA）矩阵，在此基础上计算脉冲群之间的时频相似度矩阵，输入APC得到单一放电源子脉冲群；最后，根据子脉冲群将多局部放电源PRPD分布划分为多个PRPD子图，提取每个PRPD子图的统计特征。在分类识别部分，首先采集单一放电源局部放电信号的“相位-幅值”数据构造 PRPD图谱并提取统计特征；然后，对粒子群优化支持向量机（Support Vector Machine With Particle Swarm Optimization, PSOSVM）分类器进行训练；最后，采用训练完成的PSO-SVM对脉冲群分离得到的 PRPD子图统计特征进行识别，诊断单一局部放电源的缺陷类型信息。

图1 多局部放电源识别流程图Fig.1 Flow chart of multiple PD sources recognition

2 基于ST的PD脉冲时频分析

ST是一种新型的时频分析方法，集成了短时傅里叶变换（Short Time Fourier Transform，STFT）与连续小波分析（Continuous Wavelet Transform，CWT）的优点[19]，可以采用脉冲x(t)的傅里叶变换X(f)进行计算，如下所示

在实际应用时，数字化测量方法得到的 PD脉冲x(t)以离散形式存储，可以表示为x(kT)，式中T为采样时间间隔，N为采样点数，k = 0, 1,…, N-1。令 τ → iT，f →n/NT，PD 脉冲的 ST 为

式中，n, i, m = 0, 1,…, N-1，X[n/NT]为 x(kT)的离散傅里叶变换

经测试，ST具有小于0.01s的快速时间响应特性，非常适合局部放电脉冲的在线实时分析。本文采用STA矩阵A来表征原始PD脉冲的时频信息，如式（5）。

为了消除局部放电脉冲幅值差异对时频分析结果的影响，采用式（6）对保存的PD脉冲进行归一化预处理，所有的 ST时频分析均是基于归一化的PD脉冲。

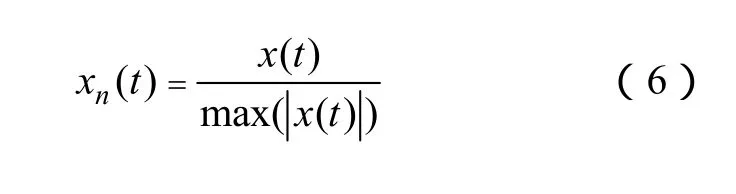
式中，x(t)表征采集的 PD脉冲，max(|x(t)|)为 x(t)的最大绝对值，xn(t)为归一化后的PD脉冲。

图2给出了一个典型的局部放电脉冲波形及其对应的 ST时频分布，其中 PD脉冲的采样率为100MS/s，持续时间为 5μs。

图2 典型的局部放电脉冲及其S变换时频分布Fig.2 A typical partial discharge pulse and its ST time-frequency representation

3 近邻传播聚类

APC是由Frey等人于2007年提出的基于样本相似度的一种聚类方法[20]。APC将所有的样本均看作潜在的聚类中心，通过消息迭代传播，从样本集中挑选出聚类中心以及每类包含的样本。

假设PD脉冲STA样本集为A={A1, A2,…, AN}，其中Ai表征第i个PD脉冲的STA矩阵，N为脉冲数。APC的参数主要有样本相似度矩阵S、偏移相量p以及阻尼因子λ。引入阻尼因子λ(∈[0, 1])是为了消除消息传播过程中发生的振荡，一般取λ=0.5可取得较好的收敛效果。p(i)表征第i个样本被选为聚类中心的倾向性，决定了最终聚类的个数。在APC算法中，p(i)被赋值给S(i, i)，S(i, i)越大，该样本被选为类中心的可能性就越大。在未知先验知识的情况下（实际中无法事先获知某个脉冲属于哪一个放电源），可假设每个样本成为类中心的可能性相同，将所有的S(i, i)均设为同一个数值。此时，p(i)越大，APC输出的聚类数目则越多；p(i)越小，最后的聚类数目越小。B. J. Frey同样给出了所有样本p(i)相等时p(i)的取值范围：pmax和pmin。当 p(i)= pmin意味着聚类结果仅有一类；而p(i) = pmax则对应着聚类数目最大值（样本数）。

采用APC进行多局部放电源脉冲群分离时，首先需要计算 PD脉冲之间的相似度，以构造样本相似度矩阵S。PD脉冲本身存在极性，而ST得到的是 PD脉冲时频分布矩阵，能够消除正负半周脉冲极性不同的影响。本文采用式（7）计算 PD脉冲STA矩阵的相似度，即：“时频相似度”。

式中，S(i, j)表征第i个PD脉冲STA矩阵Ai与第j个脉冲STA矩阵 Aj的相似度，m和n分别为STA矩阵的行数与列数，和为 STA矩阵 Ai和 Aj的均值。为了找到最优类中心及对应的聚类样本，APC采用了吸引度（Responsibility）r(i, k)和归属度（Availability）a(i, k)两种消息进行迭代传播。APC算法的实现步骤详见文献[20]。

4 指纹特征与分类器设计

采用ST+APC脉冲群分离算法，多局部放电源脉冲群被划分为多个子脉冲群，通过提取子脉冲群特征和设计分类器，即可实现子脉冲群局部放电缺陷类型的识别。

本文从最大放电量-相位Hqmax(φ)、平均放电量-相位 Hqave(φ)、放电次数-相位 Hn(φ)以及放电次数-放电量 Hn(q)等四个PRPD图谱中提取偏斜度 sk、陡峭度ku、峰值个数pe、不对称度asy以及相关系数cc等27维特征，构造识别局部放电子脉冲群缺陷类型的特征指纹库，这些特征参量的物理意义及计算表达式详见[21-23]。

分类器设计是PD缺陷识别的另一个重要内容。支持向量机（Support Vector Machine, SVM）是一种基于数理统计理论与结构风险最小化准则的新型机器学习技术，能够有效克服传统分类器的“过拟合”和“维数灾”问题，并且具有较好的泛化能力。基于 LIBSVM 工具箱[24]，本文采用径向基函数（Radial Basis Function, RBF）构建SVM分类器，并利用粒子群优化（Particle Swarm Optimization,PSO）算法[25]对SVM的核参数g和惩罚因子c进行寻优，应用训练完成的 PSO-SVM分类器对 PRPD特征进行分类，识别子脉冲群的缺陷类型。

5 局部放电试验结果分析

5.1 典型的变压器内部局部放电缺陷模型

为了模拟变压器内部油纸绝缘系统的局部放电，参照以往的研究工作[26-28]，设计了三种典型的缺陷模型：①绝缘内部气隙放电模型；②油中沿面放电模型；③油/空气分界面放电模型，依次简记为G、S、I类放电。三种放电缺陷模型的电极结构如图3所示。

图3 人工缺陷模型Fig.3 Artificial defect models

图3a为G类放电缺陷模型，采用三层直径80 mm的纸板通过环氧树脂粘接而成，并在中间层的中间制作了一个直径为 2mm的圆孔以模拟绝缘内部气隙放电。上下层绝缘纸板厚度均为1mm，中间层绝缘纸厚度为0.2mm。在图3b中，由直径为25mm柱-板电极施加在直径为 80mm、厚度为 2mm的绝缘纸板上模拟S类放电。图3c缺陷模型用于模拟I类放电，当电压超过一定值时，在油和空气的分界面将发生发电。分界面到上电极和分界面到下电极的距离分别为h1=5mm和h2=10mm。模型中绝缘纸和矿物油在试验之前均进行真空浸油预处理，真空浸油预处理步骤参见文献[29]，试验过程中所有缺陷模型均置于矿物油中，试验装置及接线图在文献[30]里有详细描述。

G、S、I类放电的起始放电电压分别为5.5kV、20kV和21kV，采用脉冲电流法测量局部放电多个工频周期的局部放电数据，采样率为 100MS/s，并从中提取 PD单次脉冲波形与对应的相位-峰值数据。试验时，首先对单一缺陷模型进行试验，通过发生稳定放电的施加电压来确定试验条件，再进行两两组合的多局部放电源缺陷模型试验。

5.2 脉冲型干扰的抑制

脉冲型干扰（Pulses-Shaped Noises, PSN）的抑制是局部放电监测的难题。由于脉冲型干扰的波形常常与局部放电脉冲具有相似的特征，采用常规的小波去噪（Wavelet De-Nosing, WDN）等方法难以去除，以至于脉冲型干扰常常被保存至PRPD图谱中。ST+APC脉冲群分离算法为抑制脉冲型干扰提供了一个可行的思路：通过计算含有脉冲型干扰的脉冲群之间的时频相似度，采用 APC得到分离结果，使局部放电脉冲群在有效聚集的同时，与脉冲型干扰可靠分离。

图4为缺陷模型G在8kV下的PRPD分布，包含2 077个脉冲。从图中可以看出，在相位110º附近有一簇干扰脉冲，具有明显的相位聚集特性。对2 077个脉冲计算时频相似度矩阵S，由S计算得到pmax= 0.902 5和pmin= -374.162 7。设置p(i)= -100，输入S和p，APC给出聚类数目为2以及对应的子类脉冲群：类#1和类#2。类#1和类#2脉冲群的 PRPD分布、类中心脉冲波形以及对应的时频分布如图5a～5f。从 PRPD分布可以较为明显地看出，类#1具有鲜明的相位分布区间，并且正负半周较为对称，为局部放电脉冲群；类#2则呈现出明显的相位聚集特性，为脉冲型干扰。由此可知，ST+APC较好地实现了脉冲型干扰的抑制。从脉冲波形可以看出，类#2波形具有一定的脉冲振荡特性，然而频率却较局部放电脉冲低很多；两者的S变换时频分布也具有明显的差异。

图4 P1缺陷模型的放电PRPD分布图谱Fig.4 PRPD pattern of the defect models of P1

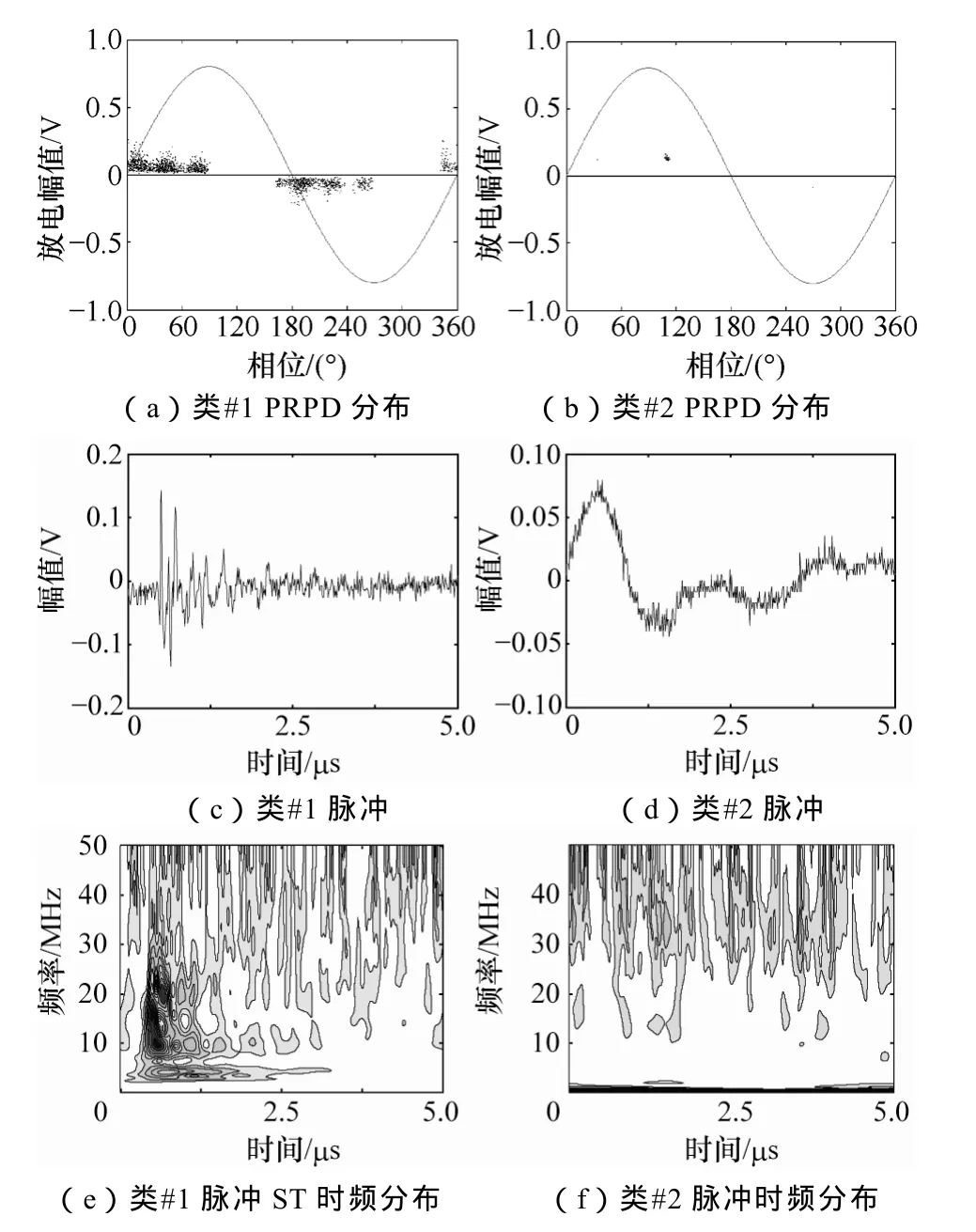
图5 P1缺陷模型的放电PRPD分布图谱Fig.5 PRPD pattern of the defect models of P1

经过仔细排查，发现类#2的脉冲群来源于实验室用于进行电热老化试验的恒温油槽。从示波器上观察，该脉冲型干扰脉冲会随着该恒温油槽的关闭和开启呈现出对应的消失和出现。油槽中内置有旋转电机，分析认为图4中的脉冲型干扰可能来源于该旋转电机，其脉冲信号通过地线耦合至测量系统中。PSO-SVM对类#1脉冲群PRPD统计特征的识别结果为G类，与真实试验缺陷模型吻合。

5.3 绝缘内部放电与油中沿面放电识别

图6 P1和P2混合缺陷模型的放电PRPD分布图谱Fig.6 PRPD pattern of the mixed defect models consist of P1 and P2

图6为G和S组成的混合缺陷模型在20kV下的PRPD分布，包含3 481个放电脉冲。从图6中可以看出，采集到的混合缺陷模型的PRPD分布较为复杂，放电脉冲分布在三个相位区间：0º～120º、160º～300º和 340º～360º，包含了两种不同的放电脉冲：①较为密集的小幅值放电脉冲；②放电较为稀疏的大幅值放电脉冲。

对采集的3 481个脉冲计算时频相似度矩阵S，由S计算得到pmax= 0.984 0和pmin= -423.621 5。设置p(i) = -100，将S和p输入APC进行脉冲群聚类，APC给出聚类结果类#1和类#2，2个子类包含的脉冲个数分别为2 454和1 027，对应子类的PRPD分布如图7a和7b所示。从PRPD子图来看，类#1脉冲群的幅值较小，相位主要集中在0°～90°、160°～270°和 340°～360°范围内，与文献[28]和文献[31]中气隙缺陷模型的局部放电相位分布都很接近。与类#1不同，类#2脉冲群的幅值相对较大，相位主要集中在0°～90°和180°～270°两个区间，属于典型的油中沿面放电特性[32]。从图7c和7d的脉冲波形上看，类#1的脉冲波形持续时间较短，同时由于放电幅值较小，在进行数据采集时受到一定的白噪声干扰，在脉冲后半段的毛刺很多；而类#2的脉冲波形的放电幅值较大，波形光滑，持续时间也较类#1更长。从图7e和7f的时频分布上看，类#1和类#2脉冲的大部分能量都主要集中在10MHz～25MHz之间，类#2脉冲在低频部分的能量比类#1更大，而类#1脉冲由于受到白噪声毛刺的影响，其时频分布较类#2脉冲更为杂乱。PSO-SVM对类#1和类#2的识别结果分别为G类和S类，与实际缺陷模型相符，较好地验证了ST+APC脉冲群分离算法的有效性。

图7 P1和P2混合缺陷模型放电脉冲群分离结果Fig.7 PD pulses separation results of the mixed defect models consisting of P1 and P2

5.4 油中沿面放电与油/空气分界面放电识别

图8为S和I混合缺陷模型的局部放电PRPD分布，试验电压为24kV，包含3 343个脉冲。计算脉冲的时频相似度矩阵S，并基于S计算得到pmax=0.993 6和pmin= -609.110 7。设置p(i)= -100，输入S和p，APC给出脉冲群聚类数目为2，对应的类#1和类#2的PRPD分布、类中心脉冲波形及其时频分布如图9所示。

图8 P2和P4混合缺陷模型的放电PRPD分布图谱Fig.8 PRPD pattern of the mixed defect models consisting of P2 and P4

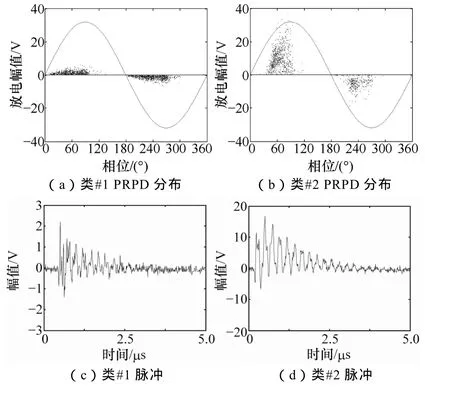
图9 P2和P3混合缺陷模型放电脉冲群分离结果Fig.9 PD pulses separation results of the mixed defect models consisting of P2 and P4

从PRPD分布上看，原始脉冲群被划分为放电幅值相对较小和脉冲幅值较大的类#1和类#2：类#1的相位分布区间为 0°～90°和 180°～270°，与沿面放电的相位分布特性吻合；类#2的相位区间为45°～100°和 200°～270°，与文献[26]中报道的分界面放电的相位分布类似。因此，从直观上观察，ST+APC成功分离了油中沿面放电与空气/油分界面放电混合放电源脉冲群。从脉冲波形上看，类#1和类#2的脉冲波形存在一定的相似性，然而类#1振荡衰减更快，类#2的脉冲持续时间更长。从时频分布上分析，类#1脉冲的频率范围主要分布在10～25MHz，类#2脉冲的能量重点集中在5MHz左右，两类脉冲的时频分布上差异明显。提取类#1和类#2脉冲群的PRPD统计特征，PSO-SVM对两个子类脉冲群的识别结果分别为S类和I类，再次验证了ST+APC和PSO-SVM的有效性。

6 讨论

6.1 ST较PD脉冲的优点

以上的分析结果表明ST+APC能够有效去除脉冲型干扰和分离多局部放电源脉冲群。基于 ST的时频分布较原始 PD脉冲的优点可以由图 10来说明，图10a和10b分别为图9类#1的正负半周归一化 PD脉冲。通常，计算这两个脉冲之间的相似度有两种处理方法：①采用两个脉冲的绝对值信号；②将第2个脉冲进行反向处理。采用上述两种方法计算得到的两个脉冲相似度分别为0.769 2和0.830 5。图10c和10d为两个脉冲的ST时频分布，其对应的时频相似度为 0.945 3。由此可知，ST能够显著提高同一局部放电源脉冲群之间的相似度。

图9c和9d分别给出了两个不同局部放电源的脉冲波形，两个脉冲波形的相似度分别为0.487 7，而对应的时频相似度为0.495 6，并没有发生明显的变化。由此可知，ST较原始PD脉冲波形的优点在于，ST不仅可以显著提高同一局部放电源正负半周的脉冲相似度，而且可以保持不同局部放电源的脉冲相似度不发生明显变化，较原始脉冲波形能够获得更好的APC聚类分离结果。

图10 典型的正负半周局部放电脉冲及其时频分布Fig.10 Typical PD pulses of positive and negative cycles and their time-frequency representations

6.2 与T-F方法的比较

ETFA是目前研究较多的多局部放电源识别方法，本文提出的ST+APC分离算法与ETFA存在着一定的差异，两种方法的主要异同点分析如下：

（1）两种方法均是通过脉冲时频分析衍生而来。基于ST的PD脉冲时频分析得到的是一个时频分布矩阵，ETFA得到的是等效时宽与等效频宽两个参数，结果可呈现在时-频2D平面上，较 ST+APC算法具有更好的可视化效果；

（2）ST+APC分离算法是基于脉冲的时频相似度矩阵，能够根据脉冲之间的相似度和输入的偏移向量给出聚类数目及对应的子类脉冲群。ETFA需要跟其他聚类算法（如k-均值、模糊C-均值等）进行配合得到最终分离结果，聚类数目往往需要人工手动输入，不利于在线智能诊断；

（3）ETFA的时频参数会在很大程度上受到脉冲宽度的影响，如果脉宽设置不当，容易导致脉冲群在时-频平面上的交叉和重叠。ST+APC方法不受脉宽的影响，对 PD原始数据采用一定的脉宽提取单次脉冲波形计算脉冲时频相似度后，即可进行多局部放电源脉冲群的分离。

6.3 APC重要参数p的影响

除了时频相似度矩阵S外，偏移相量p是影响APC聚类结果最重要的参数。目前，对于偏移相量p有三种赋值策略：①假设所有样本（N为样本数）作为潜在聚类中心的概率相同，即设定 p(1)=p(2)=…= p(i) =…= p(N)[33]；②设定偏移相量p为相似度矩阵S中值的加权相量[34]；③通过构建目标函数，将p(i)的自适应优化嵌入到APC聚类过程中，最后给出最佳聚类结果和对应的p(i)值[35]。第①种和第②种在实际中应用最多，第③种策略目前研究还较少，最优目标函数的确定是该赋值策略研究的难点，并且，迭代优化p(i)需要较长的时间。

本文也尝试采用第②种方法来设置偏移相量p，然而聚类结果往往呈现“过分离”的情况，即：APC将多局部放电脉冲群划分为很多个子类，给缺陷类型识别带来了较大麻烦。当采用第①种赋值方法，将每个放电脉冲作为聚类中心的概率设为相同，通过设置p(i)=-100，对两种放电源同时存在的情况取得了较好的脉冲群分离效果。但是，在出现四个及以上放电源时，采集的PRPD分布将会十分复杂，如何设置合理的 p(i)值将会对最终分析结果产生较大影响。

6.4 下一步的工作

本文对ST+APC算法的验证采用包含两个缺陷多局部放电脉冲群数据，下一步的工作将采用包含更多放电源的局部放电数据对算法的有效性和p值的选择进行分析，通过大量的试验数据建立 p(i)与时频相似度矩阵S之间的关联，为ST+APC算法应用于现场变压器局部放电的诊断提供理论依据。同时，未来将会在多局部放电源脉冲群分离的基础上，研究单一放电源局部放电的不同发展阶段的放电规律，进一步明确绝缘劣化过程中的局部放电发展过程。同时，局部放电发生的位置、缺陷承受电压的不同、缺陷处放电的发展状况以及绝缘材料种类等因素对算法可靠性的影响，也是今后需要进一步探索的重点。

7 结论

（1）提出了基于S变换的局部放电脉冲时频分析方法，ST时频矩阵能够融合局部放电的时域和频域信息，消除局部放电脉冲极性的影响。并且，S变换具有快速时间响应特性，非常适合局部放电脉冲的在线实时分析。

（2）构建了基于脉冲时频相似度的近邻传播聚类算法分离多局部放电脉冲群，通过计算脉冲的ST时频相似度，对每个脉冲设置相同的偏移参数，输入近邻传播聚类得到脉冲群分离结果，将原始脉冲群划分为几个具有相似时频特性的子脉冲群。

（3）从PRPD分布的四个统计图谱中提取了27维统计特征，采用 PSO-SVM识别得到子类脉冲群的缺陷类型。对实验室的含噪局部放电数据和两两组合的多局部放电源缺陷数据的分析结果表明，ST+APC算法能够较好地用于去除脉冲型干扰和实现多局部放电源脉冲群分离。

[1] Liao R J, Yang L J, Li J, et al. Aging condition assessment of transformer oil-paper insulation model based on partial discharge analysis[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2011,18(1): 303-311.

[2] Mazzetti C, Mascioli F M F, Baldini M, et al. Partial discharge pattern recognition by neuro-fuzzy networks in heat-shrinkable joints and terminations of XLPE insulated distribution cables[J]. IEEE Transactions on Power Delivery, 2006, 13(4): 1035-1044.

[3] Swedan A, EI-Hag A H, Assaleh K, et al. Acoustic detection of partial discharge using signal processing and pattern recognition techniques[J]. Insight, 2012,54(12): 667-672.

[4] Li J, Jiang T Y, Harrison R F, et al. Recognition of ultra high frequency partial discharge signals using multi-scale features[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2012, 19(4): 1412-1420.

[5] Chang W Y. Application of fuzzy C-means clustering approach and genetic algorithm to partial discharge pattern recognition[J]. International Review of Electrical Engineering, 2012, 7(4): 5213-5220.

[6] Chang H C, Kuo Y P, Lin H W. Partial discharge recognition system for current transformer using neural network and 2D wavelet transform[J]. IEEJ Transactions on Electrical and Electronic Engineering,2012, 7(2): 144-151.

[7] Contin A, Pastore S. Classification and separation of partial discharge signals by means of their autocorrelation function evaluation[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2009, 16(6):1609-1622.

[8] Contin A, Cavallini A, Montanari G C, et al. Digital detection and fuzzy classification of partial discharge signals[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2002, 9(3): 335-348.

[9] Cavallini A, Montanari G C, Contin A, et al. A new approach to the diagnosis of solid insulation systems based on PD signal inference[J]. IEEE Electrical Insulation Magazine, 2003, 19(2): 23-30.

[10] Cavallini A, Contin A, Montanari G C, et al. Advanced PD inference in on-field measurement. part 1: noise rejection[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2003, 10(2): 216-224.

[11] Contin A, Pastore S. Automatic separation of multiple PD sources using an amplitude-autocorrelation relation diagram[C]. Conference Record of IEEE International Symposium on Electrical Insulation, 2012: 434-438.

[12] Kuljaca N, Meregalli S, Contin A, et al. Separation of multiple sources in PD measurements using an amplitude-frequency relation diagram[C]. Proceedings of the International Conference on Solid Dielectrics,2010, 1207-1210.

[13] Hao L, Lewin P L, Hunter J A, et al. Discrimination of multiple PD sources using wavelet decomposition and principal component analysis[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2011, 18(5):1702-1711.

[14] Pinpart T, Judd M D. Differentiating between partial discharge sources using envelope comparison of ultrahigh-frequency signals[J]. IET Science, Measurement& Technology, 2010, 4(5): 256-267.

[15] Tang J, Li W, Liu Y L. Blind source separation of mixed PD signals produced by multiple defects in GIS[J]. IEEE Transactions on Power Delivery, 2010,25(1): 170-176.

[16] Koltunowicz W, Plath R. Synchronous multi-channel PD measurements[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2008, 15(6): 1715-1723.

[17] Belkov A, Obralic A, Koltunowicz W, et al. Advanced approach for automatic PRPD pattern recognition in monitoring of HV assets[C]. Conference Record of IEEE International Symposium on Electrical Insulation,2010.

[18] Kraetge A, Hoek S, Rethmeier, et al. Advanced noise suppression during PD measurements by real-time pulse-waveform analysis of PD pulses and pulseshaped disturbances[C]. Conference Record of IEEE International Symposium on Electrical Insulation,2010.

[19] Stockwell R G, Mansinha L, Lowe R P. Localization of the complex spectrum: the S transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001.

[20] Frey B J, Dueck D. Clustering by passing messages between data points[J]. Science, 2007, 315(5814):972-976.

[21] James R E, Phung B T. Development of computerbased measurements and their application to PD pattern analysis[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 1995, 2(5): 838-856.

[22] Gulski E, Krivda A. Neural networks as a tool for recognition of partial discharges[J]. IEEE Transactions on Electrical Insulation, 1993, 28: 984-1001．

[23] Birsen Y. Statistical pattern analysis of partial discharge measurements for quality assessment of insulation systems in high-voltage electrical machinery[J]. IEEE Transactions on Industry Applications, 2004, 40(6):1579-1594.

[24] Chang C C, Lin C J. LIBSVM. http://www.csie.ntu.edu.tw/～cjlin/libsvm/index.html, 2011.

[25] Eberhart R, J Kennedy. A new optimizer using particle swarm theory[C]. The 6th International Symposium on Micro Machine and Hum Science, 1995: 39-43.

[26] Cavallini A, Montanari G C, Ciani F. Analysis of partial discharge phenomenon in paper-oil insulation systems as a basis for risk assessment evaluation[C].Proceedings of the 2005 IEEE International Conference on Dielectric Liquids, 2005: 241-244.

[27] Liao R J, Yan J M, Yang L J, et al. Study on the relationship between damage of oil-impregnated insulation paper and evolution of phase-resolved partial discharge patterns[J]. European Transactions on Electrical Power, 2011, 21(8): 2112-2124.

[28] Li J H, Si W R, Yao X, et al. Measurement and simulation of partial discharge in oil impregnated pressboard with an electrical aging process[J]. Measurement Science & Technology, 2009, 20(10): 105701.

[29] Hao J, Liao R J, Chen G, et al. Quantitative analysis ageing status of natural ester-paper insulation and mineral oil-paper insulation by polarization/depolarization current[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2012, 19(1): 188-199.

[30] 杨丽君, 孙才新, 廖瑞金, 等. 油纸绝缘老化状态判别的局部放电特征量[J]. 电力系统自动化, 2007,31(10): 55-60.Yang Lijun, Sun Caixin, Liao Ruijin, et al. Partial discharge features applied in aging condition discrimination of oil-paper insulation[J]. Automation of Electric Power Systems, 2007, 31(10): 55-60.

[31] Del Casale M D, Schifani R, Testa L, et al．Partial discharge tests using CIGRE method II upon nanocomposite epoxy resins[C]. IEEE International Conference on Solid Dielectrics, 2007, 341-344．

[32] A. Cavallini, X. L. Chen, G. C. Montanari, et al.Diagnosis of EHV and HV transformers through an innovative partial-discharge-based technique[J]. IEEE Transactions on Power Delivery, 2010, 25(2): 814-824.

[33] Y Qian, F Yao, S Jia. Band selection for hyperspectral imagery using affinity propagation[J]. IET Computer Vision, 2009, 3(4): 213-222.

[34] Li X H, Su H Y, Chu J. Multiple model soft sensor based on affinity propagation, Gaussian process and Bayesian committee machine[J]. Chinese Journal of Chemical Engineering, 2009, 17(1): 95-99.

[35] Sun C Y, Wang C H, Song S, et al. A local approach of adaptive affinity propagation clustering for large scale data[C]. IEEE International Joint Conference on Neural Networks, 2009: 2998-3002.