基于虚拟同步发电机的分布式逆变电源控制策略及参数分析

1 引言

近年来，基于逆变器接口的分布式能源在电力系统中所占比重增长较快，包括中国、欧盟、美国及澳大利亚在内的一些国家和地区均制定了各自的分布式能源发展计划[1,2]。与传统电力系统中占支配地位的同步发电机（Synchronous Generator，SG）相比，基于电力电子逆变接口的分布式电源几乎不存在有利于保持系统稳定的旋转惯性和阻尼分量，其大量接入会影响到电力系统的动态响应及稳定性[3-5]。因此，如何通过适当的控制算法改善含分布式逆变电源系统的动态响应及稳定性，是一个亟需研究的问题。

针对分布式逆变电源，常见的控制策略有基于旋转坐标系解耦的电流型控制策略和下垂控制策略等[6-9]。前者主要工作在并网模式，能实现有功功率和无功功率的解耦控制，但采用该控制策略时，逆变电源不具有旋转惯性和阻尼分量，且不易实现离网运行；后者可在离网运行的逆变电源控制及功率分配中取得良好效果，但并网模式下，利用其模拟出的发电机下垂特性，可能会带来较大的暂态电流冲击，且其为系统提供惯性和阻尼以支撑电网的能力难有定论[10]。为了使分布式逆变电源模拟出类似SG所具有的旋转惯性和阻尼特性，基于SG模型与特性的虚拟同步发电机（Virtual Synchronous Generator，VSG）技术受到越来越多学者的关

注[11-16]。

文献[11]首次提出虚拟同步发电机的概念，该方案通过 SG的模型来控制逆变电源的输出电流，将其等效为受控电流源，不能运行在孤岛或自治模式。文献[14]利用SG的数学模型，在有功功率和无功功率外环控制中加入频率调节器和电压调节器，实现了分布式逆变电源的电流型VSG控制，但该控制算法中频率调节器使用一节延迟环节，并不能准确反映出 SG的转子运动特性，且实现自治模式运行时控制算法较为复杂。以上电流型VSG控制在弱电网或自治模式下难以支撑系统电压，因此，国内外的一些专家学者提出了电压型的 VSG控制技术[17-20]。文献[17]提出了能运行在并网和自治两种模式的电压型VSG控制方法，该方法模拟了SG的转子和一次调频特性，提高了系统频率的稳定性，且两种工作模式下均为电压型控制，易于实现平滑切换，但该控制算法并未考虑 SG无功环节的延迟特性及底层电压电流的内环控制。文献[18]根据SG的电磁方程、一次调频及调压控制特性提出的电压型VSG控制算法，较好地模拟出SG的外特性，取得了良好的控制效果。此外，文献[21-23]针对VSG算法的相关应用进行了研究，均在不同程度上仿真验证了其相比于传统控制算法的优势。

本文在上述文献的基础上，将 SG的转子运动方程、一次调频特性及无功调节延迟特性引入到逆变电源的控制算法中，研究了一种新型 VSG控制方法，通过对惯性时间常数、阻尼系数及延迟时间常数的不同设置，可更好地模拟同步发电机的不同特性。为提高电压电流内环控制器的响应速度，更好地模拟同步发电机特性，在综合分析比例（Proportional，P）、比例积分（Proportional Integral，PI）及比例谐振（Proportional Resonant，PR）控制器的基础上，提出采用跟踪正弦信号效果更好的 PR控制器。此外，建立了并网和自治两种工作模式下逆变电源的小信号模型，针对VSG控制算法中相关参数对系统稳定性及动态响应的影响进行了分析。最后搭建了基于VSG控制的Matlab/Simulink仿真模型及实验平台，对理论分析进行了验证。

2 分布式逆变电源控制策略

2.1 分布式逆变单元主电路结构及控制

基于 VSG控制的分布式逆变电源整体控制策略如图1所示，为更好地研究逆变单元的控制方法，忽略分布式能源自身的动态响应，用直流电压源来代替。

图1 整体控制框图Fig.1 Overall control diagram

图1中，Udc为等效直流电压源；S1～S6为IGBT开关管；R、L和C分别为滤波电感内阻、滤波电感及滤波电容；Ifabc、Icabc及Igabc分别表示滤波电感输出、滤波电容及流向公共母线的三相电流；Uabc为滤波电容三相电压，也即公共母线端电压；Pref、Qref为有功功率及无功功率设定值；Pmea、Qmea为逆变单元输出有功功率及无功功率测量值；E、φ为经VSG控制算法得到的参考电压幅值及相位角；Ua*、为经上层 VSG控制单元得到的三相电压参考值；ma、mb、mc为经内环控制得到的三相调制波。提出的基于 VSG的分布式逆变电源控制方法主要包括外环新型 VSG控制及内环 PR控制。经上层VSG控制得到参考电压瞬时值后，底层控制通过电压电流双环控制得到调制波，再经正弦脉宽调制（Sinusoidal Pulse Width Modulation，SPWM）产生脉冲来驱动开关管的通断。

2.2 有功—频率控制

因同步发电机转子具备一定惯性，其频率在较短时间内不会发生突变，根据其转子运动方程[3,24]，将虚拟惯性控制引入到分布式逆变电源的控制算法中，从而模拟出同步发电机的转子运动特性，可得分布式逆变电源的有功频率控制方程为

式中，H为虚拟惯性时间常数；ω、ωgrid分别为逆变电源及公共母线的角频率；Pmec、Pout分别为逆变电源的输入和输出功率；Kd为阻尼系数；φ为相位角。

当分布式逆变电源工作在并网模式且电网为强电网时，其频率ωgrid被钳位，无需分布式逆变电源进行调频。但当分布式逆变电源工作在孤岛或自治模式时，需要分布式逆变电源具备一定的调频能力，因此增加有功—频率下垂控制环节，构成调频控制器。即

式中，Dp为有功功率的下垂系数；ωref为角频率的参考值。

联立式（1）和式（2）可得到有功—频率控制的传递函数为则有功—频率控制框图如图2所示。当工作在并网模式时，ωref与 ωgrid相等，调频控制器不起作用，阻尼控制模块Kd(ω-ωgrid)保证分布式逆变电源频率与主电网频率一致。而当其工作在自治模式时，公共母线的频率与逆变电源的频率相等，阻尼控制模块失效，此时频率的动态响应由下垂控制决定。

图2 有功—频率控制框图Fig.2 Active power—frequency control diagram

2.3 无功—电压控制

分布式逆变电源工作在并网和自治两种模式时，无功—电压控制的目标不同。并网模式下，其控制目的是向电网输送指定的无功功率，而在自治模式中，输出的无功功率由负载决定，其主要目的是控制逆变电源的输出电压。据此思想，提出一种新型的无功—电压控制策略，如图3所示。

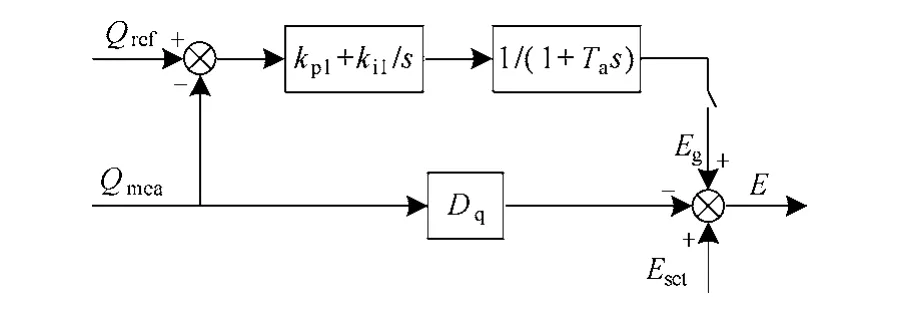
图3 无功—电压控制框图Fig.3 Reactive power—voltage control diagram

图 3中，Dq为无功功率的下垂系数；kp1、ki1为比例积分系数；Ta为延迟环节的时间常数；Eg为无功功率控制器的输出信号；Eset为分布式逆变电源端压参考值。则分布式逆变电源的参考电压可表示为

其中，PI控制器用以控制无功功率在并网模式下的输出大小，响应速度快。实际的同步发电机中，无功功率变化到新的稳态值需要一定时间，且其变化太快时会造成有功的剧烈波动，故在PI控制后面增加一阶延迟环节，这样可使无功功率缓慢地过渡到新的稳态值，减小特定情况下其对系统的冲击。而Dq则决定了系统的无功—电压下垂特性。当分布式逆变电源工作在自治模式时，应停止无功功率控制器工作，即 Eg=0，保持无功—电压下垂控制，且可通过改变端压参考值保证逆变电源端压输出值的稳定。

2.4 内环电压电流控制器

根据图 1，且忽略内阻 R，可得三相逆变电源的数学模型为[25]或P控制器来实现[25]，但由于跟踪电压信号为正弦信号，采用PI控制器会造成相位误差，从而影响系统的控制效果。而仅采用P控制器时，同样会造成一定程度的幅值和相位误差。下面通过对不同控制器的传递函数使用频域分析的方法进行比较说明。

由图4可得

式中，m0为调制比；θ为移相角。式（5）可简化为

式中，m为调制信号，m=m0cos(ωt-θ)；UC表示电容端电压。

此外，据图1可知

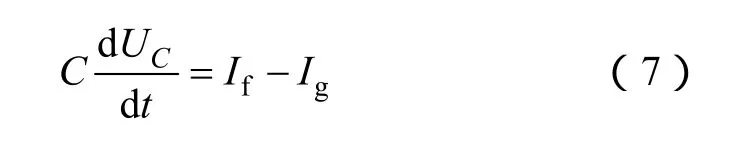
为了能及时准确地跟踪上层 VSG控制器的给定值，更好地模拟同步发电机的特性，要求内环的电压电流控制器有较高的响应速度及准确度。本文提出在电压控制环节采用跟踪控制性能较好的 PR控制器，其传递函数为[26]

式中，kp2、kr及ωc为相关控制参数，ω0=314rad/s。

内环电压电流控制框图如图4所示。

图4 内环电压电流控制框图Fig.4 Voltage and current control diagram of inner loop

图 4中，kf为电流控制环增益系数。电压控制环的 PR控制器用以使输出电压更好地跟踪其参考值，电流控制环作为补偿环节主要用来提高系统的动态稳定性。

为减小电压输出值与其参考值之间的稳态误差，使其更好地跟踪其参考值，有文献提出采用PI

则电压闭环的传递函数为

式中，电流Ig为扰动量，主电路系统相关参数见表1，此外 PR控制器参数 kp2、kr及 ωc分别为 4、100和6.5，电流控制环增益kf为0.5。分别作出U/U*在PR、PI及P 3种控制器下的Bode图，如图5所示。

表1 主电路系统参数表Tab.1 Parameters of main circuit system

图5 PR、PI及P三种控制器下U/U*的Bode图Fig.5 Bode diagram of U/U* under PR, PI and P controllers

图 5中，标注点的角频率为 314rad/s。从图中可看出，PR控制下，输出电压跟踪其给定值时幅值和相位误差几乎为零，而在PI和P控制时均有一定程度的幅值和相位误差。此外，P控制下其相位误差比 PI控制下小，两种控制下的幅值误差几乎相当，因此PR控制下，电压输出有更好的跟踪效果。

3 控制参数设计分析

3.1 系统小信号模型

由于所提控制算法可工作在并网和自治两种模式，分别对其建立小信号模型。图6所示为两种工作模式下的等效电路。其中，逆变电源的输出电压为 E∠φ；公共母线电压为 Ug∠0，即以公共母线电压为参考点；R1+jX1为线路阻抗；ZL为负载阻抗。

图6 逆变电源两种工作模式等效电路Fig.6 Equivalent circuit of inverter in both modes

并网工作模式下，逆变电源输出的视在功率为

则并网模式下，有功功率和无功功率传输的小信号模型为

并网模式下有ωgrid=ωref，联立式（3）和式（4）可得新型VSG控制策略的小信号模型为

令 X1=(Δφ′，ΔE′，Δφ，ΔE)T，根据式（12）～式（14）可得并网模式下基于新型VSG控制的分布式逆变电源的小信号模型为

自治模式下，假设负载呈阻感特性，为方便推导，假设线路阻抗与负载阻抗合起来为R+jX，则逆变电源输出的视在功率为

则自治模式下有功功率和无功功率的小信号模型为

此工作模式下，ωgrid=ω，且无功—电压采用下垂控制，则

联立式（17）～式（20），可得自治模式下分布式逆变电源的小信号模型为

式中，X2=(Δφ′，Δφ，ΔE)T。

3.2 并网模式的稳定性及参数设计分析

为分析并网模式下不同控制参数对系统稳定性的影响，采用特征值分析法针对式（15）的小信号模型进行分析。考虑到根轨迹对系统的设计和分析都很重要，首先，针对特征方程根的灵敏度进行说明。由自动控制理论可知，控制系统的传递函数T(s)对参数变化的灵敏度定义为

式中，K为变化的参数。类似地，可定义特征方程根对变量参数K变化的灵敏度为

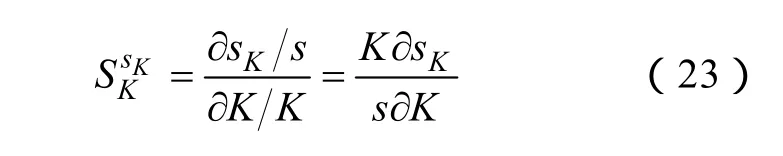
式中，s为特征方程的根。由式（23）及相关控制参数可得特征根（此处为主导特征跟）对相关控制参数变化的灵敏度大小见表2。

表2 控制系统参数及其灵敏度Tab.2 Parameters of control system and its sensitivity

由表2可看出，惯性时间常数H、阻尼系数Kd及无功下垂系数Dq的变化对系统稳定性影响较大，且由于并网模式下有功下垂控制环节不起作用，因此其灵敏度为 0。限于篇幅，下文仅对影响系统稳定性较大的几个变量进行分析。图7所示为参数H、Kd及Dq变化时并网模式的特征根轨迹。

图7a所示为H=0.5、1、3、5的情况下，Kd从1变化到 1 000的根轨迹族。可看出，系统共有 4个特征根，其中 s3、s4为变化极小的实根，对系统的稳定性几乎无影响。而 s1、s2是一对共轭复根，其变化趋势如图中箭头所指方向，且箭头所指方向Kd逐渐增加。当Kd较小时，s1、s2位于复平面的右侧，系统不稳定；随着Kd的增加，s1、s2移动到复平面的左侧，系统有较好的动态特性，此时处于欠阻尼状态，会有一定超调；当Kd继续增加时，s1、s2分别沿箭头所指方向移动到实轴上，并沿相反的方向运动，此时系统处于过阻尼状态，且s1趋近于零点时，系统的稳定裕度减小。此外，随着H的增加，特征根 s1、s2的分离点向虚轴移动，系统的响应速度变慢，其对应衰减分量的阻尼不断减小，系统的动态性能及稳定性变差。

图7b所示为Dq从0.01变化到0.4时的特征根轨迹，特征根s3和s4基本沿实轴分别向虚轴和远离虚轴的方向移动，对系统的稳定性影响不大，此时主要看主导特征根的变化趋势。可看出，随着 Dq的增加，s1、s2均向复平面的右侧移动，则系统的动态性能及稳定性会恶化，这是因为无功下垂控制是为自治模式设计的，因此参数选择时要求 Dq的值不能太大。3.3 自治模式的稳定性及参数设计分析

图7 并网模式下参数变化时的特征根轨迹Fig.7 Root locus of grid-connected inverter with variation of parameters

图 8所示为自治模式下参数 H、Dp及 Dq变化时的特征根轨迹。图8a所示为Dp=0.05、0.1、0.15、0.2下，H从0.1变化到5的根轨迹族。可看出，随着H的不断增加，共轭复根s1、s2向复平面右侧移动，系统的稳定性会随之恶化。当Dp不断增加时，特征根s1、s2更靠近虚轴，系统的稳定性也会降低，也即自治模式下大的频率波动会对系统的稳定性造成不利影响。图8b所示为Dq从0.01变化到0.4的特征根轨迹，Dq增加时，共轭复根s1、s2沿图中箭头所指方向向实轴移动，并在实轴上沿相反方向运动；随着Dq的进一步增加，s1移动到复平面的右侧，即系统不稳定。因此两种工作模式下下垂系数均不能太大。

图8 自治模式下参数变化时的特征根轨迹Fig.8 Root locus of autonomous inverter with variation of parameters

4 仿真分析

为验证所提控制策略的有效性及相关参数分析的正确性，利用Matlab/Simulink仿真软件及图1所示系统搭建了相应的仿真平台，系统仿真参数见表1和表2。

首先将本文研究的基于 VSG的控制策略与传统的电流型控制策略（Current Control Strategy，CCS）[6]及下垂控制策略（Droop Control Strategy，DCS）[25]比较，三者均工作在并网模式，如图9所示。9s之前，基于三种控制算法的分布式逆变电源的有功功率和无功功率均为 5kW、0kvar。9s时，控制三者的输出有功功率从5kW增加到8kW，可看出，CCS及DCS下输出的有功功率均可迅速上升到设定值，而VSG控制下约1s后才缓慢上升到设定值，这是因为将同步发电机的转子运动方程应用在分布式逆变电源的有功控制环，使其具备一定惯性；此外，DCS和 VSG控制下有功功率和无功功率均有不同程度的耦合，而CCS下采用的是有功和无功的解耦控制，因而其有功和无功不会相互影响。12s时，三者的无功功率均从 0上升到 1kvar，其变化趋势与有功功率变化情形相近，不同的是，受一阶延迟环节作用VSG控制下无功功率变化较慢，在一定程度上减小了其对有功功率变化的影响。

图9 3种控制策略下有功功率及无功功率对比图Fig.9 Comparison of active and reactive power under three control strategies

图10为有功功率随惯性时间常数H及阻尼系数Kd变化的波形，在时域范围内说明了H、Kd对系统动态性能的影响。

图10 主要控制参数变化对系统的影响Fig.10 Influence on system with variation of main control parameters

由图10可看出，随着H的增加，系统的动态响应缓慢，超调量较大，逐渐开始振荡。相反地，Kd较小时，系统动态响应较快，但超调量较大，达到稳定所需时间较长，即处于欠阻尼状态，随着Kd的不断增大，动态响应变慢，超调量减小，系统的阻尼不断增加。因此综合动态响应时间、超调量及达到稳定所需时间等可选择合适的惯性时间常数H和阻尼系数Kd。

图11为自治模式下的动态响应波形。初始运行时刻，分布式逆变电源单独向5kW的纯阻性负载供电，其输出的有功功率和无功功率均由负载决定，系统的频率和公共母线线电压有效值分别为50Hz、380V。设定负载在5.5s时有功功率由5kW增加到7kW，6s时无功功率由 0增加到 1kvar。从图中可看出，自治模式下有功功率和无功功率均能快速跟上负载的变化，输出的有功功率增加时，系统的稳态频率降低，这是由有功—频率下垂控制特性所决定的。同样的，由于无功—电压下垂控制的作用，分布式逆变电源输出的无功功率增加时，公共母线的电压会降低。此外，有功功率增加时，还会对系统的电压产生影响，无功功率增加时，系统的频率几乎不变，其主要影响系统的端电压。

图11 自治模型下的动态响应Fig.11 Dynamic response of the autonomous mode

5 实验验证

为充分验证所提控制策略的有效性，在额定容量为 10kVA的实际逆变电源中对所提控制策略进行试验验证，其主电路及相关控制参数与表1、表2一致。此外，控制器采用 TI公司的浮点型 DSP：TMS320F28335，开关器件IGBT采用Infineon公司的 FF450R12ME4，驱动模块采用 Concept公司的2SC018T2A0-12，实验数据及波形的采集使用Yokogawa公司的DL850示波记录仪。为方便准确地验证所提控制策略，根据已搭建的 Matlab/Simulink仿真控制模型，利用eZdsp配置好DSP的资源及端口，即可实现对仿真模型的快速控制程序代码的自动生成，在极大缩短实验验证时间的同时，最大程度上保证了系统仿真和实际应用的一致性。

基于 VSG控制的分布式逆变电源工作在自治模式时，其独立逆变带负载，与下垂控制相似，限于篇幅不再给出实验结果，下面针对其工作在并网模式的情况进行详细分析。图12和图13所示为实验测得的电压电流波形及相应的有功无功波形。由于实验条件所限，所用测量仪器不能实时测量并显示功率波形，图13是根据图12所测电压电流数据计算得到的。

图12 电压电流实验波形Fig.12 Experimental waveforms of voltage and current

图13 有功功率与无功功率波形Fig.13 Waveforms of active power and reactive power

图 12所示为相电压及相电流波形，共记录了30s的数据，下面两栏分别为有功改变过程中及无功稳定后的局部电压电流放大图。初始时刻，分布式逆变电源在所提控制策略下向电网输送的有功功率为3kW、无功功率为0。5s左右设定其向电网输送5kW的有功功率，无功功率不变，从图12左侧放大部分的电压电流相位及图 13的功率变化波形可看出：有功功率改变时，无功功率也有一定变化，这是由于所提控制策略下有功与无功之间存在一定的耦合作用造成的。有功及无功功率达到稳定后，在16s左右设定无功功率为3kvar，有功功率不变，可看到无功功率缓慢上升，这是由于所提控制策略下无功控制环加入了一阶延迟环节，且此时对有功功率波动影响较小，与理论分析一致。24s左右有功及无功功率达到其各自设定值稳态运行。

图 14所示为惯性时间常数 H分别为 0.5和 2时实验测量得到的有功功率波形，可看出，随着H的增加，系统的动态响应变慢，超调量增大，有振荡趋势，由于受到实际装置中相关器件及其他方面的影响，实测波形与仿真波形在响应时间上有所不同，但结论与理论及仿真分析一致。

图14 H变化时的有功功率实验波形Fig.14 Experimental waveforms of active power with variation of H

6 结论

（1）利用SG的转子运动方程、一次调频特性及无功电压调节、无功延迟特性构造的 VSG控制策略，较好地模拟了同步发电机的特性，且能工作在并网和自治两种模式。

（2）在推导U/U*在PR、PI及P三种控制器下传递函数的基础上，画出了其 Bode图，理论上分析了采用PR控制器能取得更好跟踪效果的原因，从而为更好地模拟同步发电机的特性提供了一定支持。

（3）建立的基于VSG控制的并网及自治模式下的小信号模型，为控制参数的选择提供了理论支撑，对相似系统的稳定性控制及分析有一定的借鉴意义。

[1] Solangi K H, Islam M R, Saidur R, et al. A review on global solar energy policy[J]. Renewable and Sustainable Energy Reviews, 2011, 15(4): 2149-2163.

[2] Tan W S, Hassan M Y, Majid M S, et al. Optimal distributed renewable generation planning: A review of different approaches[J]. Renewable and Sustainable Energy Reviews, 2013, 18: 626-645.

[3] Anderson P M, Fouad A A. 电力系统控制与稳定[M]. 王奔, 译. 北京: 电子工业出版社, 2012.

[4] 王思耕, 葛宝明, 毕大强. 基于虚拟同步发电机的风电场并网控制研究[J]. 电力系统保护与控制,2011, 39(21): 49-54.Wang Sigeng, Ge Baoming, Bi Daqiang. Control strategies of grid-connected wind farm based on virtual synchronous generator[J]. Power System Protection and Control, 2011, 39(21): 49-54.

[5] 朱晓荣, 赵猛, 王毅. 双馈感应风力发电机组复合频率控制策略研究[J]. 电力系统保护与控制, 2012,40(8): 20-24.Zhu Xiaorong, Zhao Meng, Wang Yi. Composite frequency control strategy of doubly-fed induction generator wind turbines[J]. Power System Protection and Control, 2012, 40(8): 20-24.

[6] 吴云亚, 阚加荣, 谢少军. 基于双d-q坐标系的并网逆变器控制策略[J]. 电工技术学报, 2011, 26(8):106-112.Wu Yunya, Kan Jiarong, Xie Shaojun. Control strategy for grid-connected inverter based on double d-q coordinates[J]. Transactions of China Electrotechnical Society, 2011, 26(8): 106-112.

[7] 黄杏, 金新民. 微网用分布式电源变流器下垂特性控制策略[J]. 电工技术学报, 2012, 27(8): 93-100.Huang Xing, Jin Xinmin. A voltage and frequency droop control method for microsources[J]. Transactions of China Electrotechnical Society, 2012, 27(8): 93-100.

[8] 顾和荣, 赵巍, 王雷, 等. 微电网逆变器电流下垂控制分析与实验研究[J]. 电力系统保护与控制,2013, 41(18): 45-48.Gu Herong, Zhao Wei, Wang Lei, et al. Analysis and experimental verification of current droop control for microgrid inverters[J]. Power System Protection and Control, 2013, 41(18): 45-48.

[9] 尚磊, 孙丹, 胡家兵, 等. 三相电压型并网逆变器预测直接功率控制[J]. 电工技术学报, 2011, 26(7):216-222.Shang Lei, Sun Dan, Hu Jiabing, et al. Predictive direct power control of three-phase grid-connected voltage-sourced inverters[J]. Transactions of China Electrotechnical Society, 2011, 26(7): 216-222.

[10] 曾正, 赵荣祥, 汤胜清, 等. 可再生能源分散接入用先进并网逆变器研究综述[J]. 中国电机工程学报,2013, 33(24): 1-12.Zeng Zheng, Zhao Rongxiang, Tang Shengqing, et al.An overview on advanced grid-connected inverters used for decentralized renewable energy resources[J].Proceedings of the CSEE, 2013, 33(24): 1-12.

[11] Beck H P, Hesse R. Virtual synchronous machine[C].9th International Conference on Electrical Power Quality and Utilisation, Barcelona, Spain, 2007: 1-6.

[12] 丁明, 杨向真, 苏建徽. 基于虚拟同步发电机思想的微电网逆变电源控制策略[J]. 电力系统自动化,2009, 33(8): 89-93.Ding Ming, Yang Xiangzhen, Su Jianhui. Control strategies of inverters based on virtual synchronous generator in a microgrid[J]. Automation of Electric Power Systems, 2009, 33(8): 89-93.

[13] Chen Y, Hesse R, Turschner D, et al. Investigation of the virtual synchronous machine in the island mode[C]. 3rd IEEE PES International Conference and Exhibition on Innovative Smart Grid Technologies,Berlin, Germany, 2012: 1-6.

[14] Hirase Y, Abe K, Sugimoto K, et al. A grid connected inverter with virtual synchronous generator model of algebraic type[J]. IEEE Transactions on Power and Energy, 2012, 132(4): 371-380.

[15] 张兴, 朱德斌, 徐海珍. 分布式发电中的虚拟同步发电机技术[J]. 电源学报, 2012(3): 1-6.Zhang Xing, Zhu Debin, Xu Haizhen. Review of virtual synchronous generator technology in distributed generation[J]. Journal of Power Supply, 2012(3): 1-6.[16] Bevrani H, Ise T, Miura Y. Virtual synchronous generators: A survey and new perspectives[J]. International Journal of Electrical Power & Energy Systems,2014, 54: 244-254.

[17] Gao F, Iravani M R. A control strategy for a distributed generation unit in grid-connected and autonomous modes of operation[J]. IEEE Transactions on Power Delivery, 2008, 23(2): 850-859.

[18] Zhong Q C, Weiss G. Synchronverters: Inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1267.

[19] 杨向真, 苏建徽, 丁明, 等. 面向多逆变器的微电网电压控制策略[J]. 中国电机工程学报, 2012,32(7): 7-13.Yang Xiangzhen, Su Jianhui, Ding Ming, et al.Voltage control strategies for microgrid with multiple inverters[J]. Proceedings of the CSEE, 2012, 32(7):7-13.

[20] 杜燕, 苏建徽, 张榴晨, 等. 一种模式自适应的微网调频控制方法[J]. 中国电机工程学报, 2013,33(19): 67-75.Du Yan, Su Jianhui, Zhang Liuchen, et al. A mode adaptive frequency controller for microgrid[J]. Proceedings of the CSEE, 2013, 33(19): 67-75.

[21] Sakimoto K, Miura Y, Ise T. Stabilization of a power system with a distributed generator by a virtual synchronous generator function[C]. 8th International Conference on Power Electronics and ECCE Asia,The Shilla Jeju, Korea, 2011: 1498-1505.

[22] Linn Z, Miura Y, Ise T. Power system stabilization control by HVDC with SMES using virtual synchronous generator[J]. IEEJ Journal of Industry Applications,2012, 1(2): 102-110.

[23] 吕志鹏, 罗安, 蒋雯倩, 等. 多逆变器环境微网环流控制新方法[J]. 电工技术学报, 2012, 27(1): 40-47.Lü Zhipeng, Luo An, Jiang Wenqian, et al. New circulation control method for micro-grid with multiinverter micro-sources[J]. Transactions of China Electrotechnical Society, 2012, 27(1): 40-47.

[24] 倪以信, 陈寿孙, 张宝霖. 动态电力系统的理论和分析[M]. 北京: 清华大学出版社, 2002.

[25] Li Y, Vilathgamuwa D M, Loh P C. Design, analysis,and real-time testing of a controller for multibus microgrid system[J]. IEEE Transactions on Power Electronics, 2004, 19(5): 1195-1204.

[26] 刘波, 杨旭, 孔繁麟, 等. 三相光伏并网逆变器控制策略[J]. 电工技术学报, 2012, 27(8): 64-70.Liu Bo, Yang Xu, Kong Fanlin, et al. Control strategy study for three phase photovoltaic grid-connected inverters[J]. Transactions of China Electrotechnical Society, 2012, 27(8): 64-70.