高中数学自主探究学习模式研究

2014-11-09吴荣正

教育观察 2014年14期

吴荣正

(苏州工业园区星海实验中学，江苏苏州，215021)

新课标的理念要求教学实践的改革，教师教学方式也将随着学生学习方式的改变而改变。教师只有在数学教学中不断变换课堂教学方式，才能使课堂教学生动、形象，引起学生的兴趣，使学生能够自主选择，运用自己喜欢的学习模式，在参与的过程中自主学习，使学生在教学过程中的主体地位真正得以体现。课堂采用多元化的教学方式，通过学生的参与、互动、体验和实践活动，使学生的语言综合能力和自主学习能力得以不断提高，树立学习主人翁意识。

一、探究式教学的定义

探究式教学，又称发现法教学，是指在学生学习一些概念和原理的过程中，打破传统的教学方式，把原来教师直接讲授改为在教师指导下学生通过观察、阅读、实验、讨论等方式自主学习，从而理解基本概念和原理，并达到一定效果的教学模式。

二、探究式教学的主体意识

学生是学习行为的主体，获取知识是他们自我发展的起点，而内因是其获取知识的关键所在。教师要善于激发学生学习的兴趣，学生一旦有了兴趣，其学习的过程将不再是一种额外的负担。新课标的理念指引教师要从思想观念上提升自己，要真正认识到学生才是学习的主人，要鼓励每个学生，让教师真正成为学生的学习伙伴。在探究式教学的过程中，教师要注意培养学生认真预习、专心听课、及时复习、独立完成作业、练后反思和观察的习惯。

三、加强学生学习方法的指导

(一)学会阅读

阅读是自主学习的基础。阅读时，学生首先从书本或媒体感知文字或信息，然后用大脑进行分析与综合、演绎与归纳等思维活动，并从中提取所需要的信息资料。教学实质上是教学生学会自主学习，而主动阅读能力的培养正是探究式学习的基础。

(二)学会思考

思考是学习的核心，阅读后遇到问题就要思考，解决问题的过程本质就是独立思考的过程。一个学生学习能力的高低在很大程度上取决于他的思维能力的高低。教师要通过教学的实践活动，让学生体验数学知识的发现与探究过程，引领学生从特殊到一般，再从一般到特殊地认识事物，让其体会具体问题具体分析的思维方式。

(三)学会调控

稳定而平和的心态对学习过程至关重要。学生在自主学习的过程中，有时会因成功而喜悦，有时也会因遇到困难和挫折而失落，这就需要他们能及时调整自己的心态，做到胜不骄败不馁，避免狂妄与消沉，控制自己的情绪，不断进取。要培养学生实事求是的态度，使之既能发现自身的长处又能看到自己的不足。只有能够客观地评价自己，才能制定目标，不断调整心态，采取措施，控制行为，逐步成为品学兼优的学生。

四、优化培养学生自主学习能力的探究式教学模式

(一)问题推进式

教师不断提出问题、学生不断解决问题的过程是课堂教学的重要组成部分。精心设计课堂提问，对于指导学生逐步学会思考的方法、养成良好的习惯非常重要。问题推进式的教学结构是:设置情境—提出问题—解决问题—归纳总结。

附件一(探求课题《必修一》§2.1.1:函数的概念)

学习过程:

1.情境引入(实例引入)

思考问题一:请学生回顾初中学习过的函数的概念。

思考问题二:初中学习过哪些类型的函数?

思考问题三:y=1(x∈R)是函数吗?

显然，仅用上述函数概念很难回答这些问题，因此，需要从新的高度来认识函数概念。

2.讲授新课

情景设置:在现实生活中，我们可能会遇到下列问题。

(1)估计人口数量变化趋势是我们制定一系列相关政策的依据。从人口统计年鉴中可以查得我国从1949年至1999年人口数据资料(如表1所示)，你能根据这个表说出我国人口的变化情况吗?

表1 1949—1999年我国人口数据表

(2)一物体从静止开始下落，下落的距离y(m)与下落时间x(s)之间近似地满足关系式y=4.9x2。若一物体下落2 s，你能求出它下落的距离吗?

(3)某市一天24小时的气温变化图

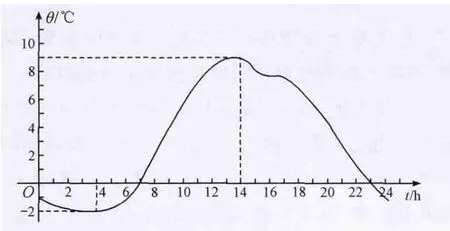
图1 某市一天气温变化图

①上午6时的气温约是多少?全天的最高、最低气温分别是多少?

②在什么时刻，气温为0℃?

③在什么时段内，气温在0℃以上?

思考问题五:如何用集合语言来阐述上述三个问题的共同特点?

3.函数概念的引入

思考问题六:根据以上共同特点，我们如何归纳出函数的定义?

(1)函数定义域:所有的输入值x组成的集合;函数的值域:所有的输出值y组成的集合。

(2)函数的构成要素:定义域、值域、对应法则。

思考问题七:函数定义域与函数定义中的非空数集A有什么关系吗?

思考问题八:函数的值域与函数定义中的非空数集B有什么关系吗?

思考问题九:函数的定义域可能为空集吗?

(二)启发讨论式

这种教学模式，是以问题为核心，以学生自主学习为前提，通过教师与学生之间相互研讨来实现教学目的的一种教学模式。这种教学模式创建了一个多向交流的平台，为学生提供了一个可以发挥各自才能的空间，能最大限度地发挥学生在学习过程中的主体作用。启发讨论式教学模式，可以兼容其他教学方式。教师可以根据既定的教学目标，结合教学内容和教学条件，选择适宜的讨论方式。如以教师为主导的讨论式:创设情境、提出问题—提供解决问题的思路、方法和材料—指导讨论—归纳总结。这种方式较适合文科内容的教学，易于发挥求异思维，使学生成为学习的主人。

附件二(探求课题§2.1.1:函数的图像)

探究任务:1.会画函数图像;2.了解研究函数图像的意义。

学习过程:

思考问题一:请同学们回顾画函数图像的步骤?

学生探究活动:请同学们对初中学习的反比例函数及二次函数各举一例(给定函数的定义域)，再利用三角板、铅笔画出这两个函数的图像。

(选择优秀的画法展示，师生共同欣赏)

思考问题二:请你总结反比例函数及二次函数图像作图的经验，并与同学们分享。

思考问题三:如果改变函数定义域，你觉得函数图像会发生变化吗?

思考问题四:设函数的定义域为A，则集合P={(x，y)|y=f(x)，x∈A}与 Q={y|y=f(x)，x∈A}相等吗?请说明理由。

例题:试画出函数f(x)=x2+1的图像，并根据要求回答下列问题:

(1)比较 f(－2)、f(1)、f(3)的大小;

(2)若函数定义域为[－1，3]，求函数的值域;