一种利用互信息加权的最小二乘法丰度反演算法

赵春晖,肖健钰

(哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨 150001)

一种利用互信息加权的最小二乘法丰度反演算法

赵春晖,肖健钰

(哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨 150001)

提出了基于互信息加权的最小二乘算法丰度反演,选择互信息矩阵作为加权矩阵,从熵的角度反映了不同波段间的相关性.同时,在丰度反演过程中应用波段选择技术,降低了数据处理的复杂度.分析实验仿真结果,与传统的最小二乘算法和已有的加权最小二乘丰度反演算法相比,获得了更精确的丰度信息,反演效果得到提升,验证了该算法的可行性.

高光谱解混;丰度反演;最小二乘算法;互信息;波段选择

随着遥感技术的发展,高光谱遥感技术在民用和军事等很多领域中起着越来越重要的作用[1].混合像元大量存在于高光谱图像中,制约了高光谱遥感技术的发展.线性光谱解混主要分为端元提取和丰度反演两个步骤[2],丰度反演主要应用的方法是最小二乘算法.根据丰度约束条件不同,最小二乘法可分为:无约束最小二乘法、“和为1”最小二乘法、“非负”最小二乘法和全约束最小二乘法[3].本文的研究是基于反演效果相对较好的全约束最小二乘法进行的.

传统的最小二乘法丰度反演计算过程中,平均地加权了所有波段,而实际高光谱数据受到大气传输等多种不确定因素的影响,不同波段对于丰度反演的有益贡献是不同的[4].为解决上述问题,提出了加权矩阵最小二乘法丰度反演,该算法突出波段间的互异性,使各个波段有不同的最小二乘误差权值,因此获得了更好的反演效果[5].为了得到更加精确的混合像元丰度信息,本文从熵的角度选择互信息矩阵作为加权矩阵,根据不同波段间的相关性强弱来确定权值大小.通过仿真实验,将该算法与传统最小二乘法及已有的加权矩阵最小二乘法进行比较,分析实验结果,证明互信息加权矩阵算法的丰度反演效果得到了提升.

1 最小二乘算法丰度反演

1.1 传统最小二乘算法丰度反演

假设需要处理的高光谱图像中存在P个端元e1-ep,任意的图像像素矢量x都可以被描述成这P个端元在适当丰度值α1,α2,…,αp下的线性混合,具体公式如下:

其中,E是由e1,e2,…,ep组成的端元矩阵,n为误差.将式(1)建模为最小二乘误差问题[6],如式(2)所示:

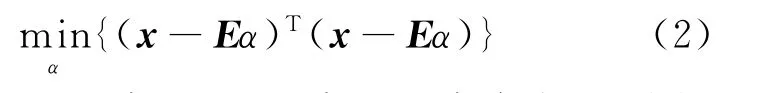
在满足全约束最小二乘法约束条件的前提下,求解丰度值α1,α2,…,αp.

1.2 加权矩阵最小二乘算法

由式(2)可以看出,最小二乘误差平均地加权所有波段,即假定了所有波段对最小二乘误差的影响是相同的.对高光谱数据而言,这通常并不正确.作为传统最小二乘法的推广,通过将式(2)中引入一个加权矩阵A[5],得到加权的最小二乘法公式.

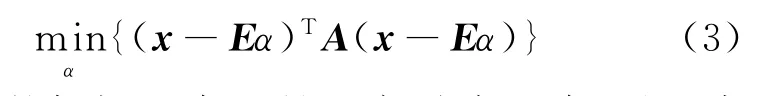
引入的加权矩阵A是正定对称矩阵,因此式(3)可进行如下变形:

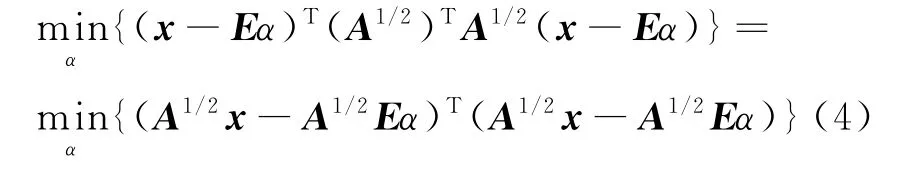
使用线性变换ξA进行如下定义:

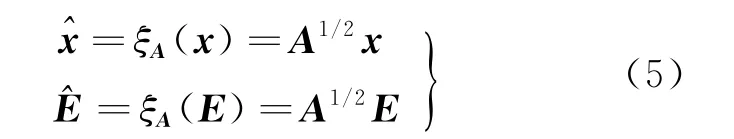
一个A矩阵加权的最小二乘算法可以由ξA进一步简化成:

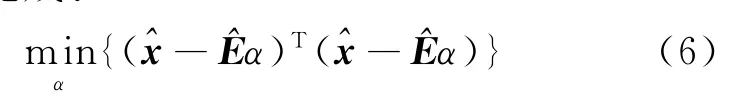
由式(6)可以看出,传统的最小二乘算法求解过程完全适用于加权矩阵最小二乘算法.

1.3 加权矩阵的选择

加权的最小二乘法丰度反演算法成功的关键,是寻找到一个使得各个单独频段最小二乘误差权值合适的加权矩阵A.Chang从参数估计、模式分类和正交子空间投影三个不同的信号处理角度解读线性光谱混合模型,并提出四种有效的加权矩阵[5].本文对其中三种加权矩阵进行介绍.

1.3.1 协方差矩阵K

加权均方差著名的方法是马哈拉诺比斯距离(马氏距离)[7],它使用数据协方差矩阵的逆矩阵K-1作为加权矩阵.用K-1矩阵取代式(3)中的A矩阵得到式(7)

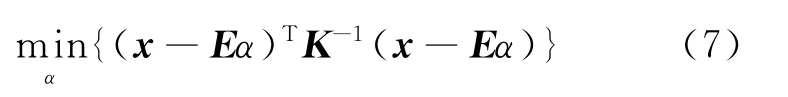
1.3.2 相关矩阵R

式(7)中最小二乘误差的加权矩阵源于马氏距离,如果将式(7)中的光谱协方差矩阵的逆矩阵K-1用光谱相关矩阵的逆矩阵R-1替换,就得到一个新的加权最小二乘误差公式:

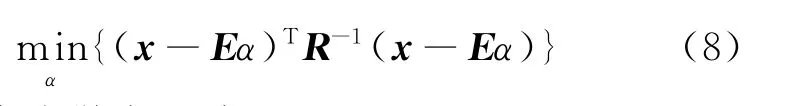
1.3.3 类内散布矩阵Sw通过{xi}in

=1给出n个训练样本矢量,P个类别分别为c1,c2,…,cp,ni是ci类的训练样本个数,定义μi为第i类样本均值,见式(9).

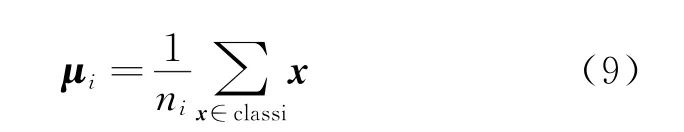
类内散布矩阵定义为:

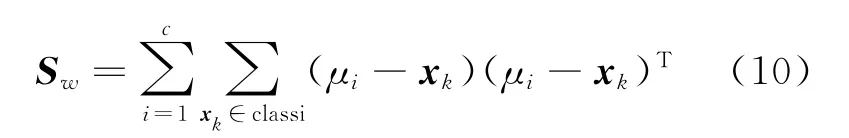
用类内散布矩阵的逆矩阵Sw-1来替换式(3)中的加权矩阵A,得到式(11).

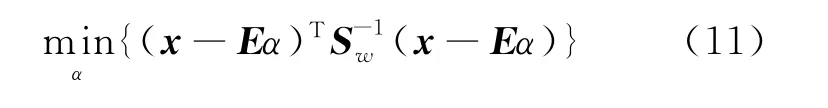
2 互信息加权的最小二乘算法丰度反演

2.1 高光谱数据波段间的互信息

互信息是为了衡量两个变量间相互依赖强弱程度而引入的,它表示两个变量间共同拥有信息的含量[8].根据互信息的性质,用互信息来衡量高光谱图像不同波段间的相关性[9].

设I是高光谱图像数据矩阵,图像的尺寸为M×N×L,其中L为高光谱图像的波段数,图像的光谱反射值用f(n,m)表示.高光谱图像的某一波段数据矩阵为I1,另一波段数据矩阵为I2,两幅图像的信息熵分别为H1与H2.两幅图像的联合熵公式表示为:

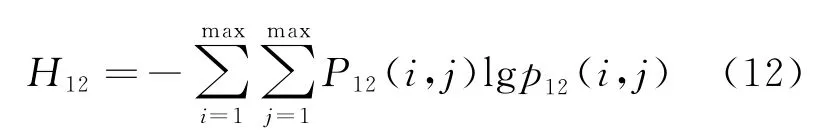
其中,联合概率P12(i,j)计算公式如下:

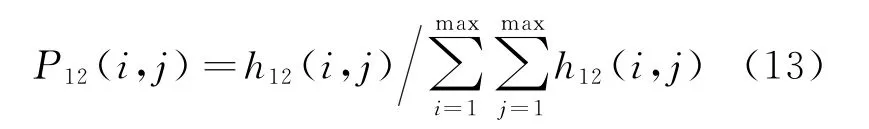
P12(i,j)中的h12(i,j)计算公式如下:

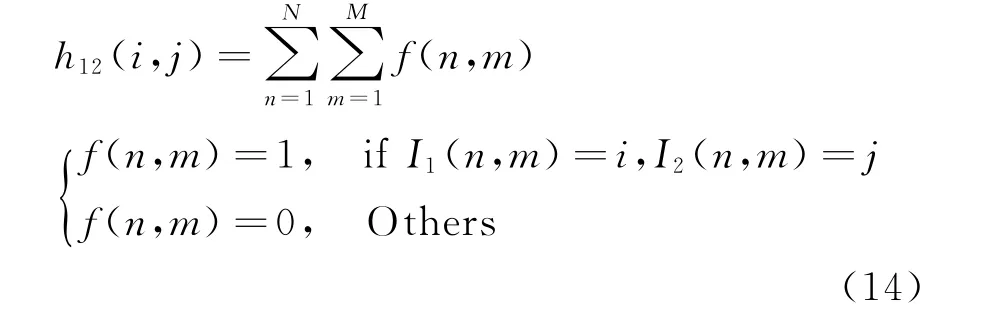
两个波段图像之间的互信息熵为:

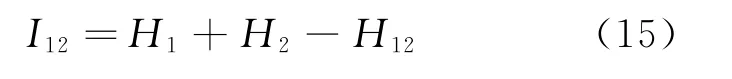
从公式中可以得出,两幅图像之间的相似度越大,它们之间的互信息值越大.

2.2 波段选择在丰度反演中的应用

由于互信息矩阵存在计算量较大的缺点,因此在丰度反演实验过程中应用波段选择技术,选择信息量大、与其他波段相关性小的波段,去除一些干扰严重以及信息量小的波段.波段选择有利于获得更加精确的混合像元丰度信息,同时降低了数据处理的复杂度.

本文运用了自适应波段选择方法[10],在丰度反演前进行波段选择,具体公式如下:

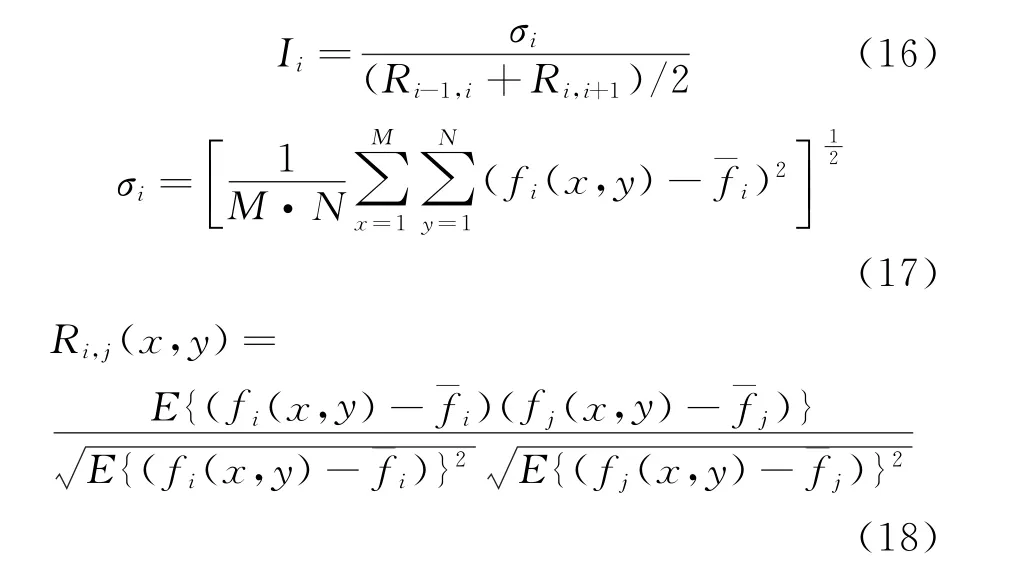
式中,Ri表示第i个波段的标准差,E为数学期望,Ri-1,i和Ri,i+1是第i个波段与其前后两波段的相关系数,Ii是第i幅图像的指数大小,M、N分别是图像的行、列像素数,fi(x,y)是第i幅图像是第i幅图像的像素平均值.

2.3 基于互信息加权的最小二乘法丰度反演

本文从熵的角度,通过波段间相关信息量的多少来衡量相关性.根据马氏距离的观点,差别较大的分量应该接受较小的权重,以此对最小二乘误差进行加权.将式(3)中的加权矩阵A选为高光谱图像不同波段间的互信息熵,可得到互信息加权最小二乘算法的公式:

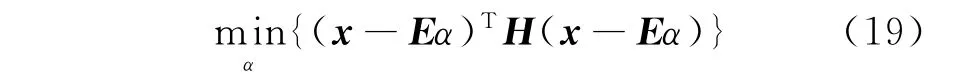
由于互信息矩阵H是正定对称矩阵,将式(19)做以下变形:

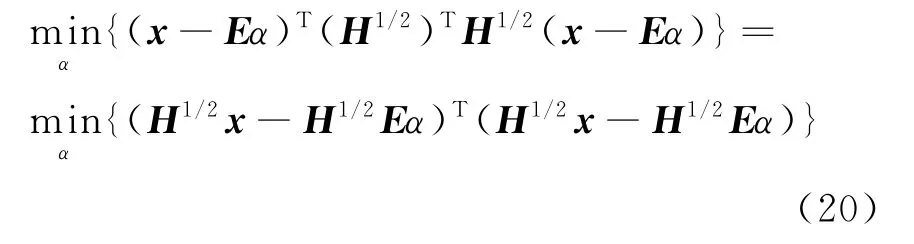
使用线性变换ξH进行如下定义:

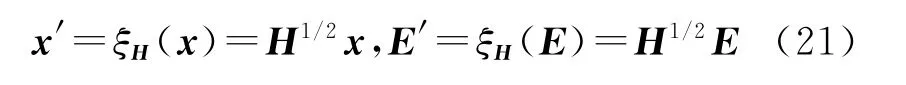
一个互信息矩阵加权的最小二乘算法可以由ξH进一步简化成:

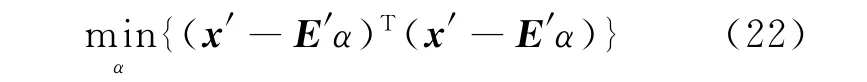
3 实验仿真及结果分析

本文的实验仿真数据选用的是AVIRIS高光谱遥感图像,该图像是1992年6月在美国印第安纳州西北部印第安遥感试验区拍摄.实验所用的高光谱图像数据共包含100个波段.从图像中选择了玉米、牧物、灌木、干草、建筑这5种地物作为样本,用来仿真传统最小二乘法及加权矩阵最小二乘法丰度反演的效果.用于实验仿真的高光谱数据的各类地物像素总个数见表1.

表1 实验地物像素总个数Table 1 The total number of land cover pixels for the experimental objects

本实验的数据均可看成纯像元,即对于某类地物的任意一个像素,该类地物的丰度值为1,其他4种地物的丰度值为0.将5种最小二乘法丰度反演的反演结果进行列表对比,表中分别列举了丰度值在0.95以上、0.97以上及丰度值为1的像元的个数,以及三个阈值下5种地物正确反演的像元总数.表2为传统最小二乘法丰度反演统计结果,表3为协方差矩阵加权的最小二乘法丰度反演统计结果,表4为相关矩阵加权的最小二乘法反演结果,表5为类内散布矩阵加权的最小二乘法反演结果,表6为互信息加权的最小二乘法正确反演个数统计结果,通过波段选择技术,选择了效果较好的50个波段得到互信息矩阵.

表2 传统最小二乘法正确反演的像元个数Table 2 The number of correctly inversion pixels for traditional least squares algorithm

表3 协方差矩阵加权最小二乘法正确反演的像元个数Table 3 The number of correctly inversion pixels for covariance matrix weighted least squares algorithm

表4 相关矩阵加权最小二乘法正确反演的像元个数Table 4 The number of correctly inversion pixels for correlation matrix weighted least squares algorithm

表5 类内散布矩阵加权最小二乘法正确反演的像元个数Table 5 The number of correctly inversion pixels for scatter matrix weighted least squares algorithm

表6 互信息加权的最小二乘法正确反演的像元个数Table 6 The number of correctly inversion pixels for mutual information weighted least squares algorithm

从统计数据中可以看出,表2中传统最小二乘法地物1和地物2正确反演的像元个数较多,而地物3、4、5丰度值在0.95以上的像元个数分别占实验仿真中该类地物像元总数的12.85%、21.47%和11.84%,反演效果不好.加权矩阵最小二乘法在5种地物上得到的反演效果相对较为均衡,5种地物反演统计结果都能令人满意.已有的三种加权矩阵在本实验中反演效果最好的是相关矩阵,5种地物在丰度值0.95以上的正确反演的像元总数占用于仿真实验的总像元数的38.99%.而本文给出的互信息加权的最小二乘法反演结果显示,地物3、4、5丰度值在0.95以上的正确反演的像元个数分别占到了用于仿真实验的该类地物总像元个数的41.50%、28.83%、36.84%.同时,5种地物在丰度值0.95以上的正确反演的像元数占用于仿真实验总像元数的40.24%,与其他三种加权矩阵最小二乘算法相比,该算法在阈值以上的正确反演的像元数更多,获得的丰度信息更准确.

为了更直观地观察反演效果,图1给出了丰度反演效果图.从图中可以看出,传统最小二乘算法部分区域图像信息丢失较为严重.互信息加权矩阵最小二乘算法没有表现特别糟糕的地物类别区域,显现出了更多的细节信息.

图1 丰度反演理论图像与仿真效果图Fig.1 The theoretical image and simulation results of abundance inversion

4 结 论

本文给出了基于互信息加权的最小二乘高光谱混合像元丰度反演算法.加权矩阵选用互信息矩阵,通过波段间相关信息量的多少来衡量相关性,从而确定权值.同时利用自适应波段选择方法,在不影响丰度反演准确性的同时降低了数据处理复杂度.分析实验结果,互信息加权最小二乘算法较传统二乘算法反演效果有较大改进,与已有的加权矩阵最小二乘算法相比,正确反演的像元总数上也更有优势,得到了更加准确的丰度信息.

[1]王立国,赵春晖.高光谱图像处理技术[M].北京:国防工业出版社,2013:226244. (Wang Ligo,Zhao Chunhui.Processing Technigues of Hyperspectral Imagery[M].Beijing:National Defense Industry Press,2013:226244.)

[2] 成宝芝,赵春晖,王玉磊.结合光谱解混的高光谱图像异常目标检测SVDD算法[J].应用科学学报,2012,30(1): 8288. (Cheng Baozhi,Zhao Chunhui,Wang Yulei.SVDD Algorithm of Spectral Unmixing for Anomlay Detection in Hypersectral Images[J].Journal of Applied Sciences, 2012,30(1):8288.)

[3] 罗小波,赵春晖,潘建平,等.遥感图像智能分类及其应用[M].北京:电子工业出版社,2011:142 154. (Luo Xiaobo,Zhao Chunhui,Pan Jianping,et al.Remote Sensing Image Intelligent Classification and Its Application [M].Beijing:Publishing House of Electronics Industry, 2011:142154.)

[4] 李二森.高光谱遥感图像混合像元分解的理论与算法研究[D].郑州:解放军信息工程大学,2011:1035. (Li Ershen.Research on Theory and Algorithms of Mixing Pixels Decomposion in Hyperspectral Remote Sensing Images[D].Zhengzhou:The PLA Information Engineering University,2011:1035.)

[5]Chang C I,Ji Baohong.Weighted Abundance-constrained Linear Spectral Mixture Analysis[J].IEEE Transaction on Geoscience and Remote Sensing,2006,44(2):378388.

[6]Chang C I,Heinz D.Constrained Subpixel Target Detection for Remotely Sensed Images[J].IEEE Transaction on Geoscience and Remote Sensing,2000,38 (3):11441159.

[7]Settle J J.On the Relationship between Spectral Unmixing and Subspace Projection[J].IEEE Transaction on Geoscience and Remote Sensing,1996,34(4):10451046.

[8]刘华文.基于信息熵的特征选择算法研究[D].长春:吉林大学,2010:4666. (Liu Huawen.A Study on Feature Selection Algorithm Using Information Entropy[D].Changchun:Jilin University,2010:4666.)

[9] 黄杰贤,杨冬涛,龚昌来.互信息熵与区域特征结合的图像匹配研究[J].激光与红外,2013,43(1):98 103. (Huang Jiexian,Yang Dongtao,Gong Changlai.Research on Image Match Based on Mutual Information Entropy and Regional Feature[J].Laser&Infrared,2013,43(1): 98103.)

[10] 刘春红,赵春晖,张凌雁.一种新的高光谱遥感图像降维方法[J].中国图象图形学报,2005,10(2):218222. (Liu Chunhong,Zhao Chunhui,Zhang Lingyan.A New Method of Hyperspectral Remote Sensing Image Dimensional Reduction[J].Journal of Image and Graphics,2005,10(2):218222.)

【责任编辑:李 艳】

An Abundance Inversion Algorithm Based on Mutual Informationweighted Least Squares Error

Zhao Chunhui,Xiao Jianyu
(College of Information&Communication Engineering,Harbin Engineering University,Harbin 150001,China)

In order to highlight the distinctness between the bands and obtain more accurate abundance of mixed pixels,the least squares error algorithm is used,which is based on weighted matrix for the abundance inversion.Abundance inversion based on mutual information-weighted least squares error algorithm is presented,mutual information from the perspective of entropy to reflect the correlation between different bands.Band selection technology is adopted in abundance inversion to reduce the complexity of data processing.Compared with the existing weighted matrix and traditional least squares error problem,the analysis of the experimental result shows the feasibility of this algorithm.

hyperspectral unmixing;abundance inversion;least squares error algorithm;mutual information;band selection

2095-5456(2014)01-0045-05

TN 911.2

A

2013 10 21

国家自然科学基金资助项目(61077079);教育部博士点计划基金资助项目(20102304110013);黑龙江省自然科学基金重点资助项目(ZD201216).

赵春晖(1965),男,黑龙江汤原人,哈尔滨工程大学教授,博士生导师.