近平板状食品速冻过程冻结时间的数值计算与实验验证

章 斌，秦 轶，邓其海，丁 心，李长栋

（1.韩山师范学院生物学系，广东潮州 521041；2.广东中兴绿丰发展有限公司，广东河源 517000）

冻结作为升华干燥前的一道重要工序，是加工冻干食品的一个重要过程，对原料的冻结品质、冰晶体形成的大小和速率、升华干燥时间的长短以及成品品质（如复水性、内部组织结构等）均有很大影响；冻结时间是影响冻结过程质量的关键因素之一，也是设计和评价食品冻结设备及考虑食品冻结生产工艺时的一个重要因素[1-2].若能在实际生产中较精确地预测不同几何形状食品的冻结时间，则可使冻结设备的设计、操作和控制得到优化；并能在保证产品品质的前提下合理安排冻结过程和降低冻结生产成本.目前对食品冻结时间的确定主要有经验公式预测和数值计算预测两种方法[3-4]，前者方便简单，但误差较大；而数值计算方法预测精度高，适用性较广，较常运用的主要有固定空间步长变时间步长法、固定时间步长变空间步长法、自变量变换法、热面移动法、焓法和显热容法等[5-6].本文以柠檬片和香蕉片在冻库中近似大平板状的盘装冻结状态为实验对象，采用完全隐式差分法对平板状食品一维冻结过程的温度模型进行求解，描述其冻结过程，计算香蕉在不同冻结温度下的冻结时间，并进行实验验证，以期为实际生产提供参考依据.

1 材料与方法

1.1 材料与设备

柠檬：广东中兴绿丰发展有限公司提供；香蕉：九成熟，新鲜、无病虫害或机械损伤.

BD-255LT型超低温冰箱（额定最低温度为-120 ℃）：华凌集团有限公司；VC9804A+型万用表：深圳胜利高电子科技有限公司.

1.2 冻结实验过程：

参照文献[2]的方法，将温度探头1 置于预处理好的物料中心，探头2 置于样品上方约3 cm处以测量环境温度.将样品与温度探头1、2均固定在传热性能差的泡沫盒上，整个冻结实验在超低温冰箱内进行；为减少实验过程箱温的波动，预先在低温箱内制备一些已冻结好的冰块，利用其潜热的释放来保证环境温度恒定.记录样品的初始温度，将装有样品和连接VC9804A+型数字温度显示仪的泡沫盒放入冰箱内并计时，每3 s记录样品的中心温度，具体装置示意图见图1所示.

图1 冻结装置示意图

2 冻结过程分析与物理模型

2.1 冻结过程

食品冻结过程存在大量有相变的热传导问题，不论是球状食品，还是平板状食品，其冻结过程一般经历如下3个阶段[2]：第1阶段，样品温度由初温迅速降低，直到表面温度达到冰点温度Tf；第2阶段，相变在表面发生，由表及里推进至中心面，相变完成；第3阶段，样品温度继续下降，至冻结终温.上述3个阶段的冻结时间则对应包括：预冷时间（Pre-cooling time），物料从初温降到冰点所耗时间；冻结时间（Freezing time），从冰点至物料中的水分全部冻结所耗时间；继续冻结时间（sub-cool⁃ing time），物料从完全冻结降温至终温所耗时间.

2.2 冻结过程的物理模型

建立一块厚度尽可能小且为2 L的平板状食品在温度为T∞的低温环境中冻结的物理模型，该食品的上下表面均与环境发生热交换，与冷却介质间的对流换热系数为α；由于传热的对称性，取其中心面上半部分进行研究，以表面为坐标零点，方向朝中心面建立坐标，如图2所示.同时，将平板状食品沿厚度X 轴方向n 等份，以表面为结点i=1，结点示意图见图3.

食品中的液体是一种多组分溶液，其相变是在一个微观区域内进行且相变时固液区的成分会不断变化[7-8]；同时，物料的热物性参数也会在冻结过程的3个阶段发生数值上的改变，对数值模拟和计算过程及计算结果的精度均造成一定影响.因此，在平板状物料的实际冻结过程中，尽可能增大平铺面积可使本实验对象柠檬和香蕉中的液、固体成分假定为均匀分布且属于一维相变[5]，并使计算过程得以简化.

图2 平板状食品冻结过程示意图

图3 平板状食品结点划分示意图

3 数值计算与实验验证

3.1 导热微分方程

平板状食品在冻结过程中的热传递是一个复杂、不稳定、变物性参数的一维瞬态导热问题，同时，食品的潜热只是在冻结冰点时才有，可将冻结潜热换算到冻结冰点区间内的比热容中.因此，用来描述该导热问题的一维非稳态微分方程为[8-9]：

式（1）中：T- 食品各几何点的温度；t- 冻结进行的时间；λ- 热导率；C- 定压比热容； ρ- 密度；x- 几何点在厚度方向上的坐标值

初始条件：T(x,0)=T0(0 ≤x ≤L)

对流边界条件：

绝热边界条件：

在移动的相变界面s(t)上，满足温度连续条件与能量守恒条件[10]：

3.2 导热方程差分格式的建立

柠檬片和香蕉片冻结过程的第1阶段和第3阶段均属单相均匀物质的降温过程，且其表面为对流换热边界，在其表面上方虚拟一结点i=0，原来的表面就成为内点i=1.

以第1阶段为例，可将描述该阶段冻结过程的式（1）差分离散为，

其中

中心面看作绝热对称，所以可在中心面下方虚拟一结点i=n+2，原来的绝热边界点变为内结点，有：

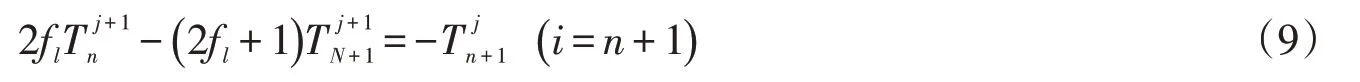
对第3阶段的方程差分将式（1）～式（9）中的下标l（液相）变成s（固相）即可.

第2阶段为相变过程，将整个过程分为固态区、液态区和相变界面三个区，再对每个区进行单独处理，相变过程示意图如图4所示.

对流换热边界隐式差分方程为

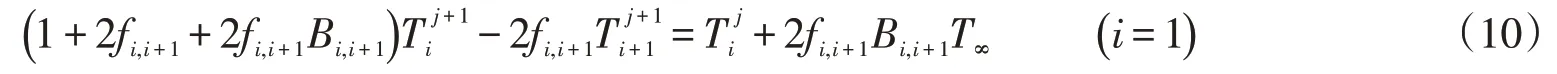
其中

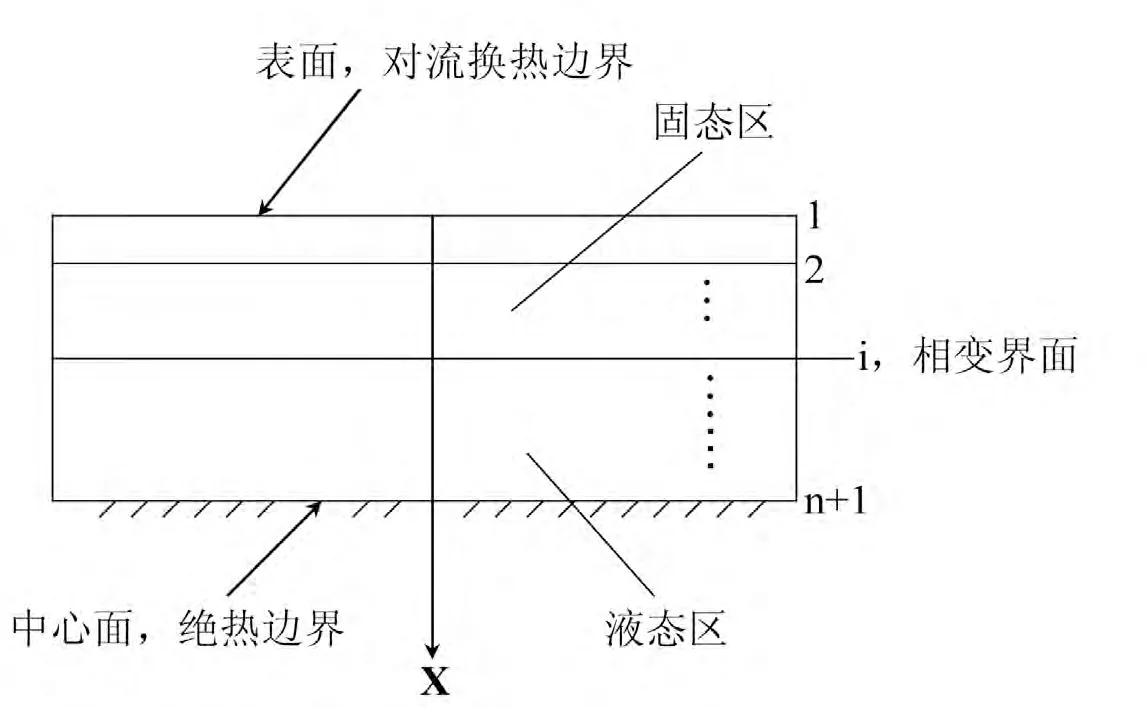
图4 相变过程示意图

固态区：将导热方程（1）差分离散并化简得

式中

温度连续方程

液态区

绝热边界

过冷过程

3.3 数值计算法封闭方程组的构成

（6）式～（16）式中的各式组合起来即构成封闭方程组，给定Δt 的值，对上述封闭方程组采用Visual C++6.0语言软件编程，进行求解计算得到方程组的解，从而可得到中心结点的温度值.

3.4 实验验证

将柠檬和香蕉的热物性参数代入（6）式～（16）式所构成的封闭方程组进行数值计算[11-12]，计算条件和实验测定条件为：（i）柠檬片：介质温度T∞=-120 ℃，厚度L=1 cm，初始温度T0=26.8 ℃，对流表面传热系数α=44.45W/(m2⋅K)；（ii）香蕉片：介质温度T∞= -80 ℃，厚度L=0.6 cm，初始温度T0=19.6 ℃，对流表面传热系数α=25.07W/(m2⋅K)，结果见图5.

条件（i）和（ii）下的数值计算结果与实验结果分别如图5所示，从图中可看出：数值计算结果有明显的冻结3阶段，且-120 ℃下的第3阶段的斜率较第1阶段的斜率大，曲线更为陡峭，与实验情况相符；-80 ℃下的第3 阶段的曲线较第1 阶段变得平缓，也与实验测定结果相符.在最大冰晶生成带-1 ℃～-5 ℃间有一段水平直线，起始部分比较吻合，当温度进入-10 ℃时，曲线的重合性降低，且均是在0 ℃左右的温区产生最大的误差；随着冻结的进行，物料温度继续降低，直到接近介质温度；所以在冻结后期，实测值与预测值的曲线变得越来越吻合.为观察温度趋势，在-120 ℃和-80 ℃条件下各取5个温度点，进行误差比较，结果分别如表1和表2所示.

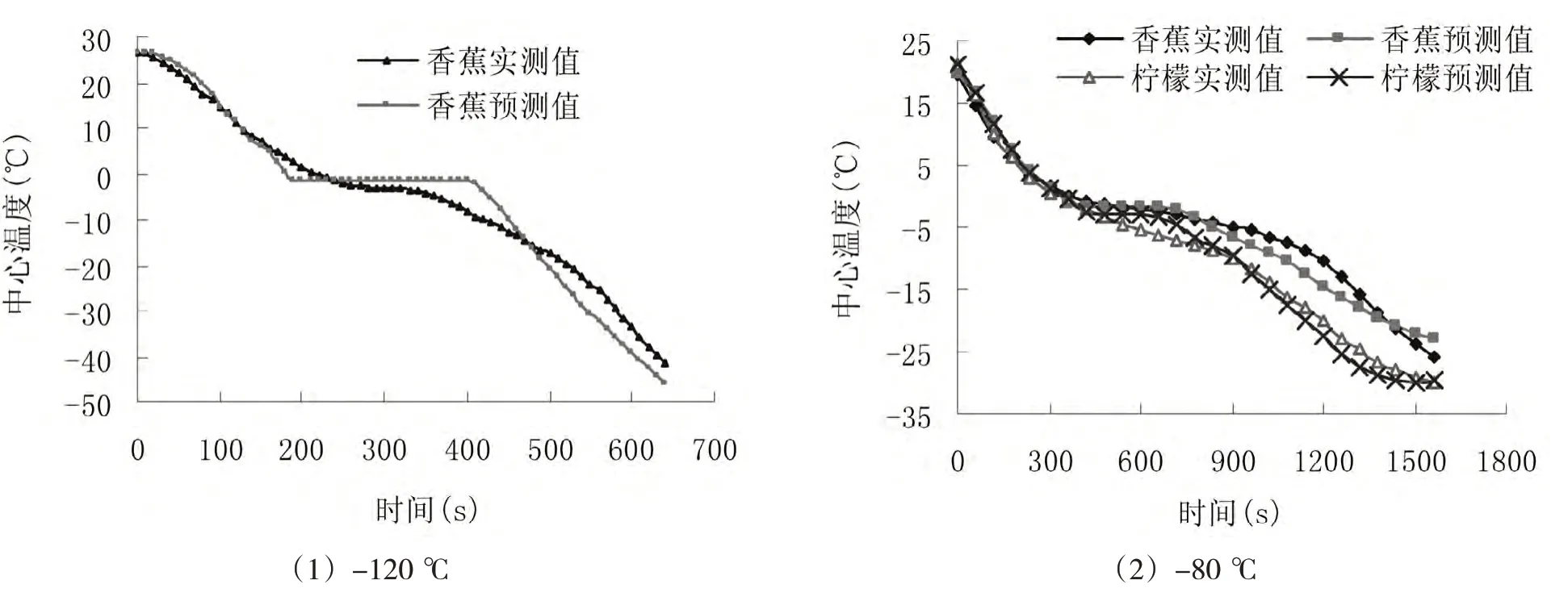
图5 不同温度下预测值与实验值的对比

表1 -120 ℃下实验值与预测值的误差比较(香蕉片)

表2 -80 ℃下实验值与预测值的误差比较

由表1和表2知，所取5个温度点的误差绝对值呈现先增大，后减小的趋势；且都在0 ℃（接近最大冰晶生成带-1 ℃～-5 ℃）时的误差达最大；之后随着样品温度的继续降低，误差逐渐缩小，这一实验结果表明物料在最大冰晶生成带的热物性参数值变化较明显，对数值计算结果的影响较大.同时，求得5个温度点的误差绝对值的平均值分别为11.81%（香蕉片、-120 ℃）、11.42%（香蕉片、-80 ℃）、6.49%（柠檬片、-80 ℃），由此看出不同物料的数值计算结果误差波动较大；综合前人的研究情况来看，为进一步提高数值计算的理论精度，适宜冻结温度和冻结速率的选择也应在实验设计时做相应考虑.而造成条件（i）的平均误差稍大于条件（ii）的平均误差的可能原因有：（1）条件（i）中物料的厚度（10 mm）较大，导致垂直于厚度方向（Y 轴方向）的物料面与冷量接触的比表面积增大，从而也就使得厚度方向的径向传热误差变大；（2）物料的几何尺寸误差，导致数值计算中边界条件的变化误差；（3）超低温冰箱内部环境温度的波动；（4）热电偶的测量端进行定位时所造成的温度探头位置的误差.

为说明数值计算方法的精度，设定物料中心温度从初温降至-20 ℃，对比数值计算值和应用广泛的简易公式计算值[13-14]，分别求得与实验值的误差，结果见表3和表4.从表3和表4可看出：数值计算方法对冻结时间的计算较经验公式有更好的适用性和精度.

表3 -120 ℃下数值计算、经验公式计算与实验值的比较(香蕉片)

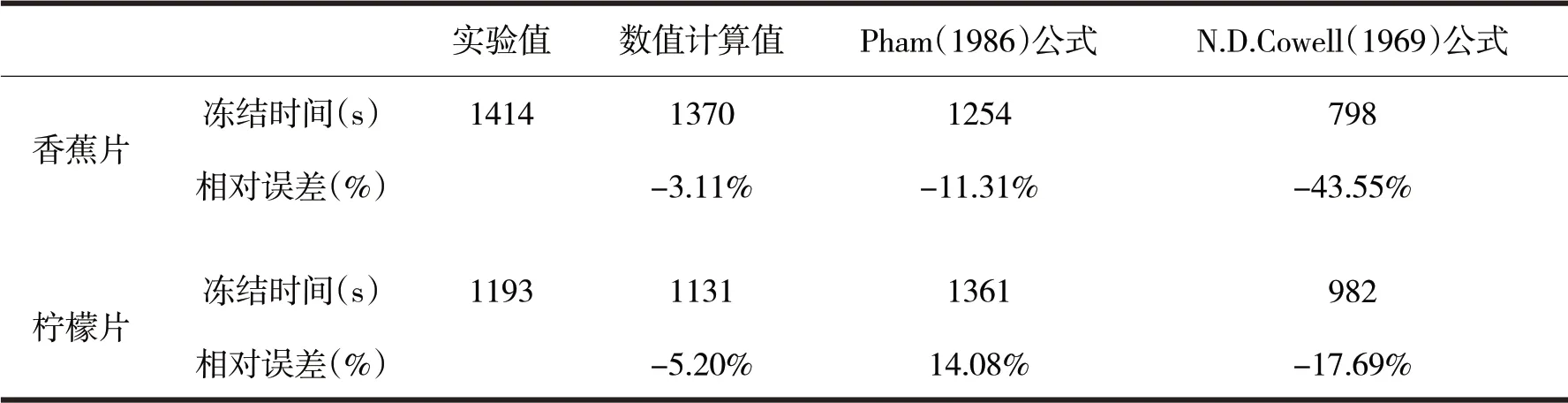
表4 -80 ℃下数值计算、经验公式计算与实验值的比较

4 结论

（1）本文采用一维非稳态热传导方程对以柠檬片和香蕉片为代表的近平板状食品的冻结过程进行数值模拟与计算，测定在-80 ℃和-120 ℃介质温度下其中心温度的变化情况，实验结果表明数值计算方法的预测值与实测值在一定程度上有较好的吻合度，且采用数值计算方法计算冻结时间比经验公式有更好的精度和适用范围，对实际生产过程的冻结时间预测有一定的实际意义和参考作用.

（2）食品冻结的实际过程相当复杂，本实验中的模拟程序主要是针对近大平板状的一维非稳态食品的冻结情况，仅是初步简单地模拟柠檬片和香蕉片的冻结过程；不论是模型精度还是实验条件的优化均有待进一步完善，如考虑在一维、二维与三维情况下，建立精度更高的数学模型以适用于复杂形状食品的冻结过程，或对冻结食品的各物性参数进行具体条件下的测定，或对样品在更多介质温度下的冻结过程进行数值模拟与实验验证以获得更详实、更可信的理论参考都是今后需继续开展的工作.

[1]章斌，侯小桢.香蕉片冻结过程的影响因素研究[J].食品工业科技，2008，29（9）：98-101.

[2]章斌，李远志.青豆速冻过程冻结时间的数值计算[J].食品研究与开发，2006，27（11）：18-20.

[3]WOINET B, ANDRIEU J, LAURENT M.Experimental and Theoretical Study of Model Food Freezing.PartI.Heat Transfer Modelling[J].Journal of food engineering，1998，35(4):381-393.

[4]LÓPEZ-LEIVA M,HALLSTRÖM B.The original Plank equation and its use in the development of food freezing rate predic⁃tions[J].Journal of Food Engineering，2003，58（3）：267-275.

[5]郭宽良，孔祥谦，陈善年.计算传热学[M].合肥:中国科学技术大学出版社，1998.

[6]曲春民，孙勇，冀卫兴.鲜食玉米冷冻加工过程的传热分析[J].食品科学，2006，27（10）：111-114.

[7]查世彤，马一太，魏东.食品热物性的研究与比较[J].工程热物理学报，2001，22（3）：275-277.

[8]杨世铬.传热学基础[M].北京：高等教育出版社，2002.

[9]姚仲鹏，王瑞君.传热学[M].北京：北京理工大学出版社，2003.

[10]屠建祥，刘宝林.黄瓜片冻结过程的数值计算及实验研究[J].上海理工大学学报，2000，22（4）：304-307.

[11]高福成.食品工程原理[M].北京:中国轻工业出版社，1998.

[12]华泽钊，李云飞，刘宝林.食品冷冻冷藏原理与设备[M].北京：机械工业出版社，1999.

[13]PHAM Q T.Simplified equation for predicting the freezing time of foodstuffs[J].Journal of Food Technology，1986(21)：209-219.

[14]关志强，戴午子，郭兆均.平板状食品冻结时间的数值预测[J].食品与发酵工业，1999，25（4）：26-30.